建坐标 构方程 解平抛

顾　岩　梅宇航

(江苏省镇江第一中学，江苏　镇江　212009)



建坐标构方程解平抛

顾岩梅宇航

(江苏省镇江第一中学，江苏镇江212009)

关于平抛运动的解答，常规的方法是利用运动的合成与分解，将其分解为两个相互垂直的直线运动，求出分运动的相关物理量，最后合成，其核心思想是“分而解之”.在实际问题的处理中，有时还可以从合运动入手，利用数学方法，构建平抛运动轨迹方程，直接求解.

平抛运动；合运动；轨迹方程

在人教版高中物理必修2“平抛运动”中，从数学层面探讨了平抛物体的运动轨迹方程，但却鲜见用平抛运动轨迹方程来解决物理问题，笔者在此略陈管见.

1　平抛物体轨迹方程的拓展构建

图1

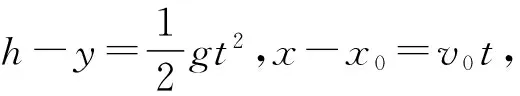
2　示例呈现

2.1利用点的坐标

例1：抛体运动在各类体育运动项目中很常见，如乒乓球运动(如图2),谈及乒乓球发球问题，设球台长2L、网高h，乒乓球反弹前后水平分速度不变，竖直分速度大小不变、方向相反，且不考虑乒乓球的旋转和空气阻力.

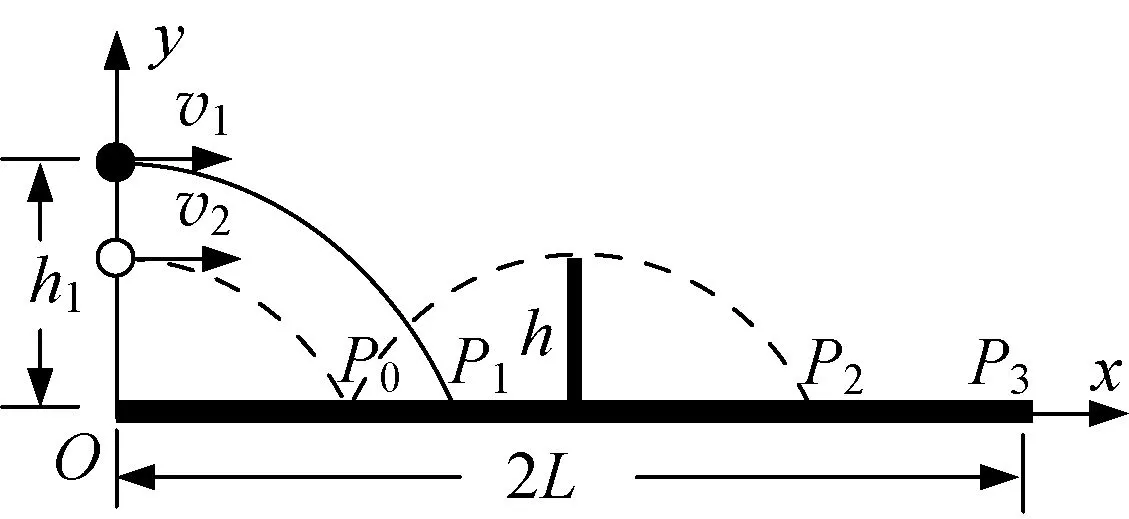
图2

(1) 若球在球台边缘O点正上方高度为h1处以速度v1水平发出，落在球台的P1点(如图2实线所示)，求P1点距O点的距离x1;

(2) 若球在O点正上方以速度v2水平发出，落在球台的P0点,且恰好在最高点时越过球网落在球台的P2(如图2虚线所示)，求v2的大小;

(3) 若球在O正上方水平发出后，球经反弹恰好越过球网且刚好落在对方球台边缘P3，求发球点距O点的高度h3.

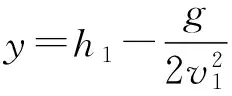
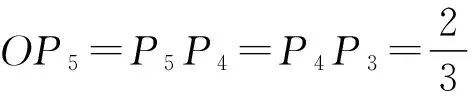
图3

解答评析:选取适当的原点建立坐标系，使得一些点的坐标成为已知，进而使问题明朗化.

2.2求出点的坐标

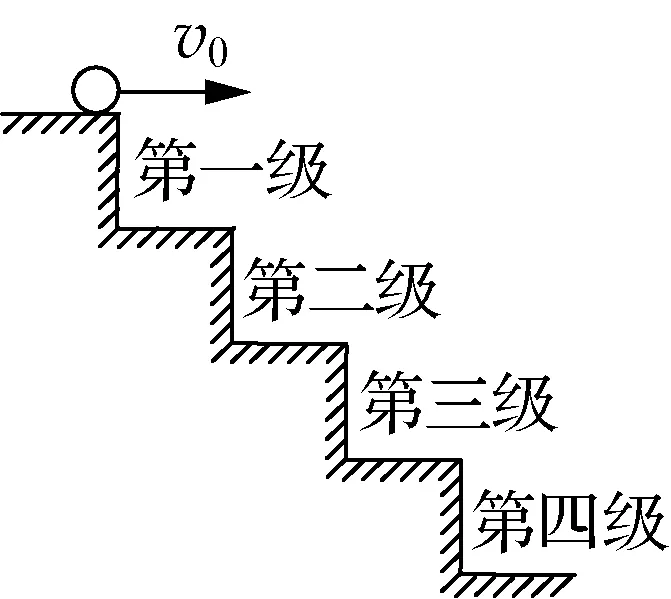
图4

例2：如图4所示，小球从楼梯上以2m/s的速度水平抛出，所有台阶的高度和宽度均为0.25m，g取10m/s2，小球抛出后首先落到的台阶是().

A. 第一级台阶

B. 第二级台阶

C. 第三级台阶

D. 第四级台阶

图5

解析:以抛出点为坐标原点建立坐标系(如图5)，将阶梯的直角边缘用直线连接起来，若落在阶梯上，则小球必须先通过边缘的连线，通过抛物线与直线的交点A的坐标即可判断小球落在第几级台阶上.

例3：小亮观赏滑雪比赛，看到运动员先后从坡顶水平跃出后落到斜坡上.如图6所示，某运动员的落地点B与坡顶A的距离L=75m，空中飞行时间t=3.0s.若该运动员的质量m=60kg，忽略运动员所受空气阻力作用，重力加速度取g=10m/s2.

(1) 求A、B两点的高度差h;

(2) 求运动员落到B点时的动能EkB;

(3) 小亮认为，无论运动员以多大速度从A点水平跃出，他们落到斜坡时的速度方向都相同.你是否同意这一观点?请通过计算说明理由.

图6

解析:(1)、(2) 略.

(3) 由于速度方向沿轨迹切线方向，而轨迹方程的一阶导数的数学意义恰为切线斜率，若能证明轨迹在与斜面的交点处的一阶导数的数值为一个与初速度无关的常量即可说明落到斜坡上的速度方向都相同.

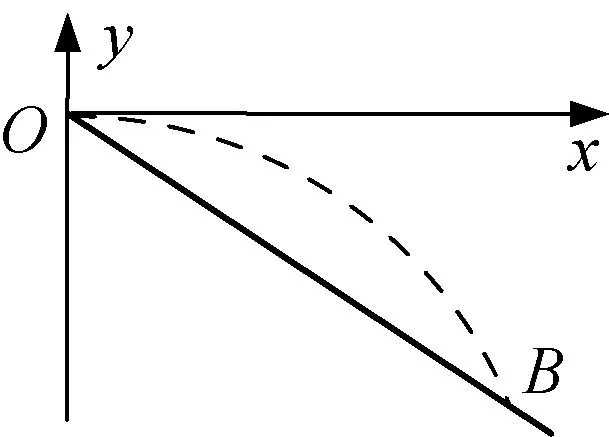
图7

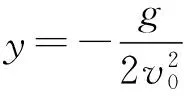
解答评析:通过平抛运动的轨迹方程与其他方程的联立，解得交点坐标，从而使问题得到有效的解决.

3　小结

从学生已有的数学知识储备出发，利用平抛运动的轨迹方程有时可以高效简捷地解决问题，更重要的意义是该做法为解答平抛问题提供了另一条思考途径，该途径的核心就是建立合理的坐标系，写出平抛的轨迹方程，然后与点的坐标共同使用.

郑永令.物理奥林匹克竞赛标准教材[M].北京:北京教育出版社，2004.