基于ABAQUS的橡胶扭转减振器固有频率预测方法研究

郭一鸣，杜晓泽，上官文斌

（1.湖北汽车工业学院汽车动力传动与电子控制湖北省重点实验室，湖北十堰442002；2.华南理工大学机械与汽车工程学院，广东广州510641）

基于ABAQUS的橡胶扭转减振器固有频率预测方法研究

郭一鸣1，2，杜晓泽2，上官文斌2

（1.湖北汽车工业学院汽车动力传动与电子控制湖北省重点实验室，湖北十堰442002；2.华南理工大学机械与汽车工程学院，广东广州510641）

在橡胶扭转减振器固有频率测试方法的基础上，提出了基于ABAQUS软件的固有频率预测方法；对橡胶材料的超弹性本构模型和黏弹性本构模型进行了试验研究；以圆鼓型轮毂橡胶扭转减振器为例介绍了固有频率有限元预测方法的实现过程，并同固有频率测试结果进行了对比，研究结果表明：本文中提出的有限元方法能在橡胶扭转减振器物理样机出来之前能对其固有频率进行准确预测，具有较强的工程应用价值。

橡胶扭转减振器；固有频率；预测方法；ABAQUS

扭转振动是发动机曲轴等旋转机械的固有特性［1］。曲轴的扭转振动会使发动机曲轴轴系在运行时产生附加的扭转交变应力，从而影响整个发动机的NVH、燃油经济性和可靠性［2］。合理控制曲轴的扭转振动至关重要。减少曲轴扭转振动最常用的方法就是在曲轴前端加装橡胶扭转减振器［3］。

橡胶扭转减振器基于动力吸振器的原理而工作，固有频率是橡胶扭转减振器最重要的性能参数之一。由于受到安装空间的限制，扭转减振器惯量环的转动惯量变化有限，因此其固有频率只与橡胶圈扭转刚度和阻尼有关［4］。橡胶圈扭转刚度和阻尼的影响因素有扭转减振器轮毂的激振频率、激振振幅以及橡胶材料类型、橡胶圈的结构尺寸、压缩比等［5］。在工程实际中，匹配扭转减振器时往往首先通过软件（例如AVL的EXCITE-designer）计算分析得到最佳的扭转减振器固有频率［6-7］。但由于橡胶扭转减振器固有频率受其结构特性和材料特性的影响，要得到具有最佳固有频率的扭转减振器产品，需要通过不断的产品试制、试验和改进等过程，导致设计效率较低、设计成本较高。［8］。因此，在橡胶扭转减振器物理样机出来之前能对其固有频率进行准确预测是非常有意义的。

笔者在橡胶扭转减振器固有频率测试方法的基础上，借助非线性有限元软件ABAQUS对橡胶扭转减振器固有频率的预测方法展开研究。

1　橡胶扭转减振器固有频率的测试

橡胶扭转减振器固有频率测试设备选用日本鹭宫（さぎのみや）扭转试验台，如图1所示。扭转减振器和加速度传感器的连接和安装关系如图2所示，扭转减振器的惯量环处于自由状态，扭转减振器的轮毂与扭转试验台的扭转激振轴连接在一起，在扭转激振轴与惯量环的外缘各安装一个单向加速度传感器。

图1　日本鹭宫（さぎのみや，Saglnomlya）扭转试验台

图2　橡胶扭转减振器固有频率测试

在固有频率测试过程中，扭转试验台的扭转激振轴对扭转减振器的轮毂产生恒定的激振振幅（0.01°）、正弦扫频（100～500 Hz）角位移激励。单向加速度传感器用来拾取扭转激振轴与惯量环的切向加速度。扭转激振轴的切向加速度拾取值可用作反馈信号，以保证扭转试验台激振振幅恒定，还可用于确定扭转减振器轮毂的切向加速度。惯量环的切向加速度与轮毂的切向加速度相除并进行傅里叶变换，得到惯量环加速度幅值的频响函数曲线，其峰值点所对应的激振频率为橡胶扭转减振器的固有频率。

当橡胶硬度为70 HA、橡胶圈压缩比为35%时，依次改变扭转试验台激振轴的激振振幅，可得到橡胶扭转减振器在不同轮毂激振振幅下惯量环加速度幅值的频响函数曲线，如图3所示。由不同频响函数曲线的峰值点所对应的激振频率即橡胶扭转减振器的固有频率，其测试结果如表1所示。

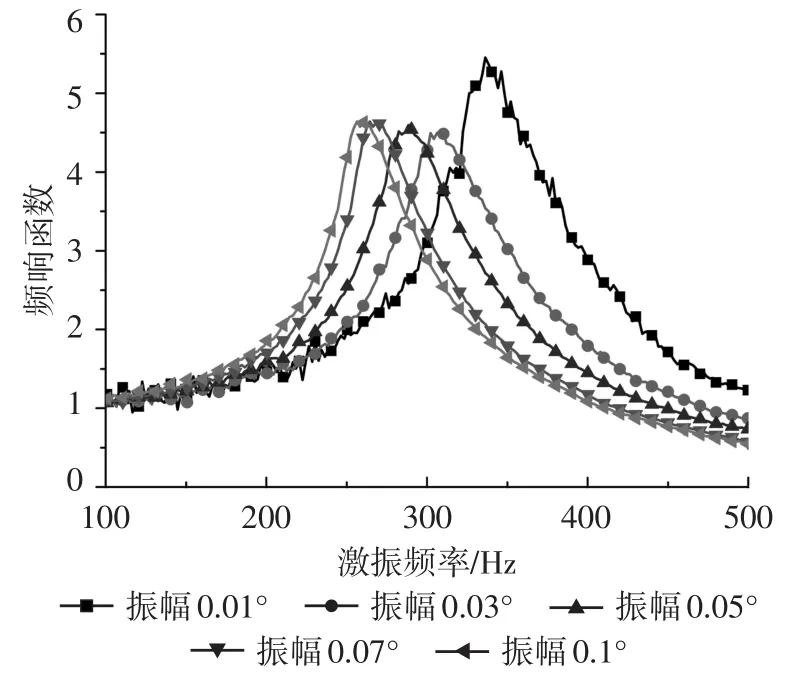
图3　橡胶扭转减振器惯量环加速度幅值的频响函数曲线

表1　橡胶扭转减振器固有频率测试值

2　固有频率的有限元法预测流程

ABAQUS是一款功能强大的工程有限元分析软件，能解决诸多复杂的非线性问题［9］。考虑到橡胶扭转减振器橡胶材料的非线性特性，采用ABAQUS软件预测橡胶扭转减振器的固有频率。基于ABAQUS的橡胶扭转减振器固有频率有限元法预测流程如图4所示。

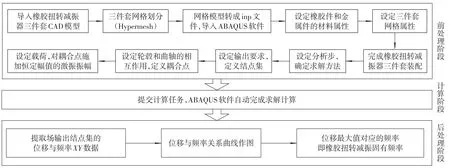
图4　基于ABAQUS的橡胶扭转减振器固有频率有限元法预测流程

在橡胶扭转减振器固有频率测试时，施加的激振振幅较小（不大于0.1°），因此在有限元预测过程中忽略振幅相关性的影响，采用橡胶超弹性和粘弹性本构模型预测橡胶扭转减振器的固有频率。

ABAQUS有限元分析主要有3个阶段：前处理阶段、求解计算阶段和后处理阶段。在3个阶段中最重要的是前处理阶段，前处理阶段的重难点是橡胶扭转减振器橡胶圈橡胶材料属性的定义，而要定义橡胶材料属性，就必须选取合适的橡胶本构模型并根据试验数据确定其参数。

3　橡胶材料的本构模型

3.1橡胶的超弹性本构模型

ABAQUS软件中的橡胶材料超弹性本构模型有Neo-Hooke模型、Mooney-Rivlin模型、Yeoh模型、Reduced-Polynomial模型和Ogden模型［10］。其中Mooney-Rivlin模型是最常用的超弹性本构模型，其应变能数学表达式为

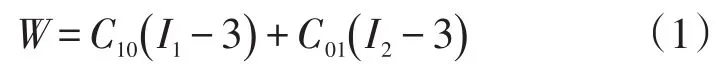
式中：C10，C01为材料常数。

为得到橡胶本构模型中的材料参数，需要开展橡胶材料的相关力学试验。经验表明：只要有橡胶材料单轴压缩和平面拉伸的试验数据，Mooney-Rivlin本构模型就能较好地表征填充橡胶的超弹性特性［11］。

橡胶材料单轴压缩和平面拉伸的测试工装、橡胶试样的尺寸如图5～6所示［12］。采用图5～6所示的试验方法，对不同硬度的各种橡胶试柱和橡胶试片进行单轴压缩和平面拉伸试验，得到橡胶变形过程中的应力-应变关系，如图7所示。利用ABAQUS软件进行材料参数拟合计算，得到不同硬度橡胶材料的Mooney-Rivlin本构模型参数如表2所示，应力-应变的试验数据与拟合数据如图7所示。由图7可知，Mooney-Rivlin本构模型的拟合精度较高，能较好描述橡胶圈橡胶材料的超弹性特性。

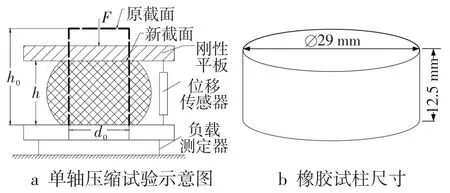
图5　橡胶试柱单轴压缩试验

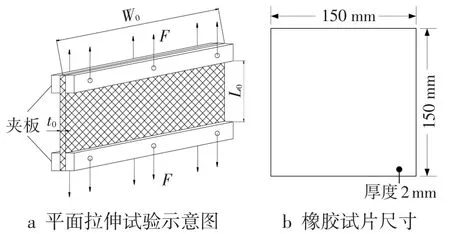
图6　橡胶试片平面拉伸试验

表2　不同硬度橡胶材料的本构模型参数

图7　橡胶变形应力-应变曲线

3.2橡胶的黏弹性本构模型

ABAQUS软件中有4种方法定义橡胶材料的黏弹性特征：Prony级数、蠕变试验数据、松弛试验数据以及正弦激振试验频率相关性试验数据［10］。本文中采用Prony级数本构模型来描述橡胶扭转减振器橡胶圈的黏弹性特性，本构方程为［13］

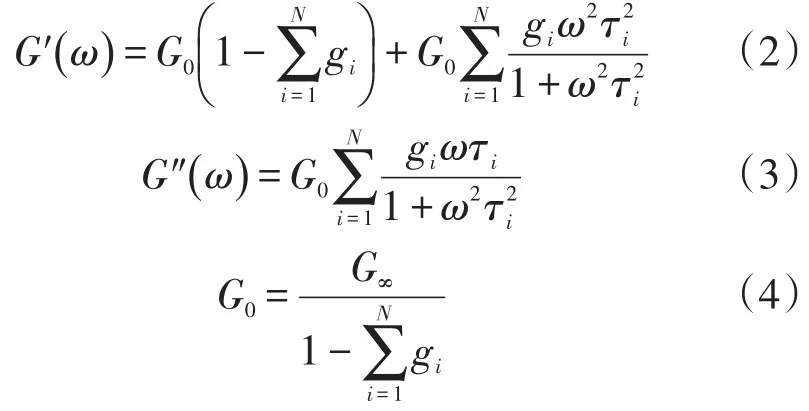
式中：G0为瞬时模量；G∞为准静态模量；gi为模量比，gi=Gi/G0。

对于橡胶扭转减振器橡胶圈而言，式（2）～（4）中的相关参数可由橡胶试片的剪切试验数据得到。剪切试验采用双层三明治结构双剪切型橡胶试片，其试验工装如图8所示［14］。

图8　双剪切型橡胶试片试验工装

由动态剪切试验可获得橡胶试片的动刚度和相位角，经过计算可得橡胶试片的剪切存储模量和剪切损失模量，根据式（2）～（3），采用最小二乘法拟合就可得到Prony级数模型本构方程中的参数gi和τi［15］。Prony级数模型本构方程的阶数N取值不同，得到的参数gi和τi也不同。当Prony级数本构方程的阶数N为3时，橡胶试片橡胶材料剪切存储模量和剪切损失模量的拟合值和测试值对比如图9所示，由图9分析可知：当阶数N为3时，Prony级数本构方程能较好地描述橡胶试件橡胶材料的黏弹性特性。

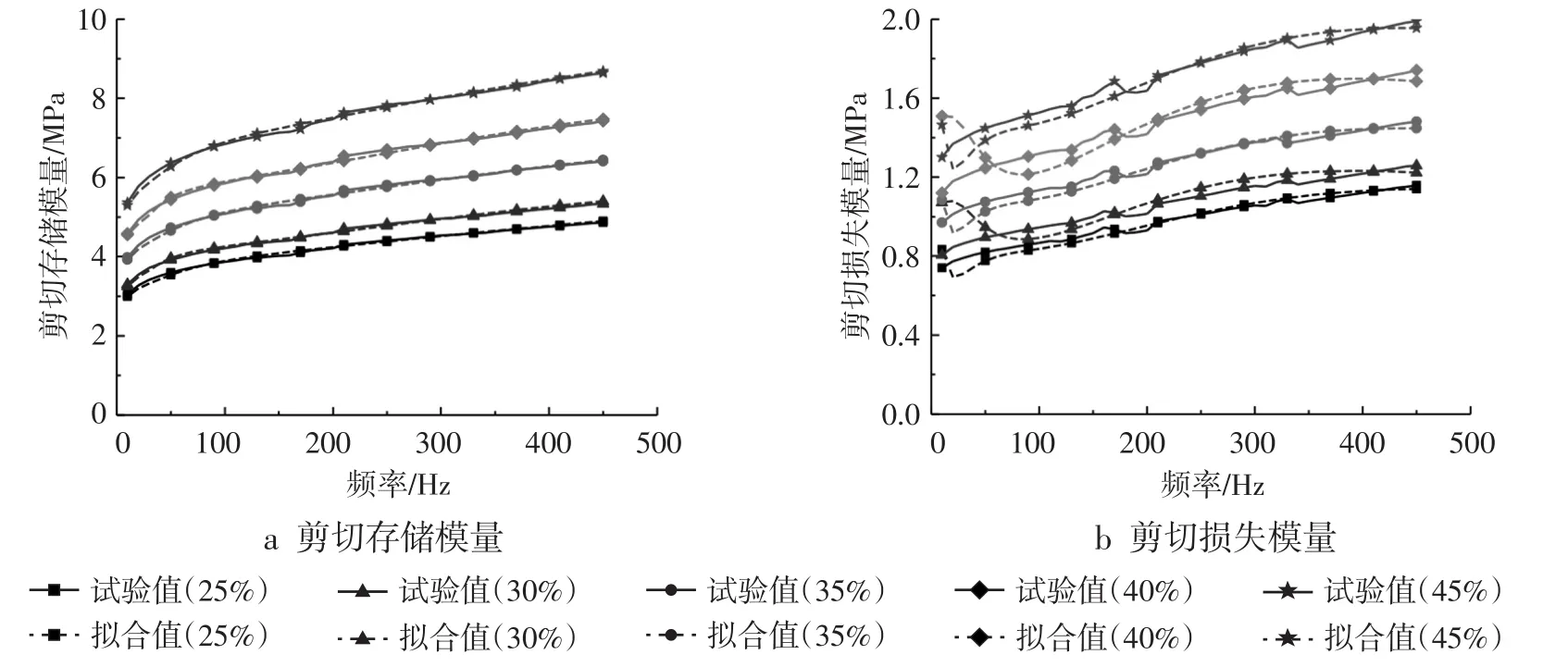
图9　橡胶试片橡胶材料剪切模量曲线（70 HA，N=3）

4　固有频率有限元预测方法的实现

某款圆鼓型轮毂橡胶扭转减振器的结构及尺寸如图10所示，橡胶硬度为70HA，橡胶圈压缩比为35%，有关尺寸参数如表3所示。

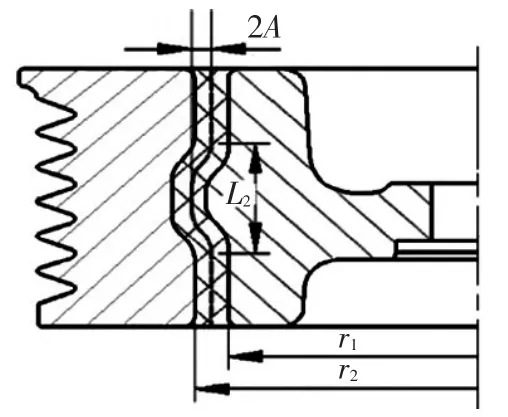
图10　橡胶扭转减振器的结构及尺寸示意图

表3　橡胶扭转减振器的有关尺寸参数mm

4.1橡胶扭转减振器网格划分

橡胶扭转减振器由惯量环、橡胶圈和轮毂等三件套组装而成，导入三件套CAD模型到Hypermesh软件中进行网格划分，网格模型如图11所示，网格模型相关信息汇总如表4所示。

图11　橡胶扭转减振器三件套Hypermesh网格模型

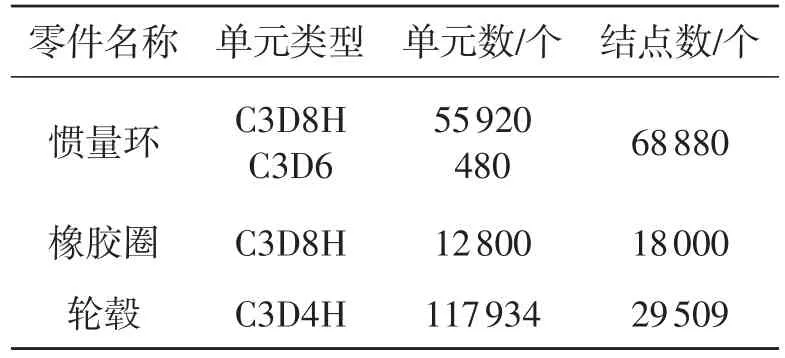
表4　橡胶扭转减振器网格模型相关信息

4.2橡胶扭转减振器有限元模型的建立

将在Hypermesh软件中已划分好的网格模型转成inp格式并导入到ABAQUS软件中，进行三件套部件的装配，建立橡胶扭转减振器有限元模型，如图12所示。在建模过程中，将惯量环内表面、轮毂外表面分别和橡胶圈绑定，定义轮毂和曲轴相互作用的耦合结点。在该耦合结点沿轮毂轴向（Y轴方向）施加激振振幅为0.1°的正弦角位移激励，为惯量环上任一结点建立响应集RESPONSE。

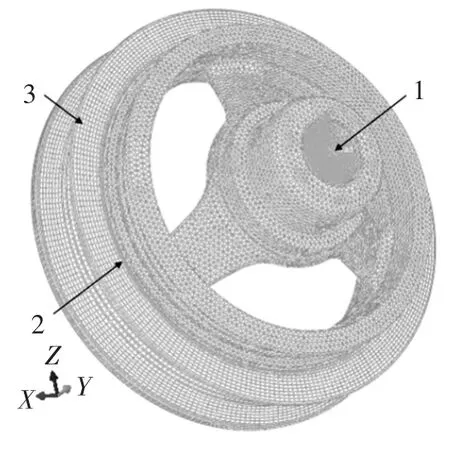
图12　橡胶扭转减振器ABAQUS有限元模型

4.3橡胶件和金属件材料属性的定义

圆鼓型轮毂橡胶扭转减振器橡胶圈的硬度为70HA、压缩比为35%，由本文中第3.1节的方法可得Mooney-Rivlin超弹性本构模型的参数C10为0.1856，C01为0.4688；由本文中第3.2节的方法可得Prony级数黏弹性本构模型的参数g1为0.3277，g2为0.1577，g3为0.4270，τ1为0.0003，τ2为0.0029，τ3为21.0612；橡胶的密度为1.2×103kg·m3。

橡胶扭转减振器惯量环和轮毂的材料均为铸铁，密度为7.3×103kg·m3，杨氏模量为2.1×103MPa，泊松比为0.3。

4.4固有频率预测结果

橡胶扭转减振器固有频率的求解选用基于直接解法的稳态动态分析方法。完成计算任务后，在场输出中选择惯量环上任一结点的切向位移U1（X轴方向）和响应集RESPONSE，得到位移和激振频率数据，其关系曲线如图13所示，该曲线中位移峰值点所对应的激振频率即该橡胶扭转减振器的固有频率。由图13可知：橡胶圈硬度为70 HA、压缩比为35%橡胶扭转减振器的固有频率为260 Hz。

图13　惯量环响应点切向位移与激振频率的关系

当橡胶硬度发生变化时，在ABAQUS软件中依次改变橡胶本构模型参数的设置，就可得到橡胶圈压缩比为35%的橡胶扭转减振器在不同橡胶硬度时的固有频率，该固有频率预测值和试验测试值的对比如表5所示。当橡胶圈压缩比发生变化时，在ABAQUS软件中依次改变橡胶本构模型参数的设置，就可得到橡胶硬度为70 HA的橡胶扭转减振器在不同橡胶圈压缩比时的固有频率（表6）。

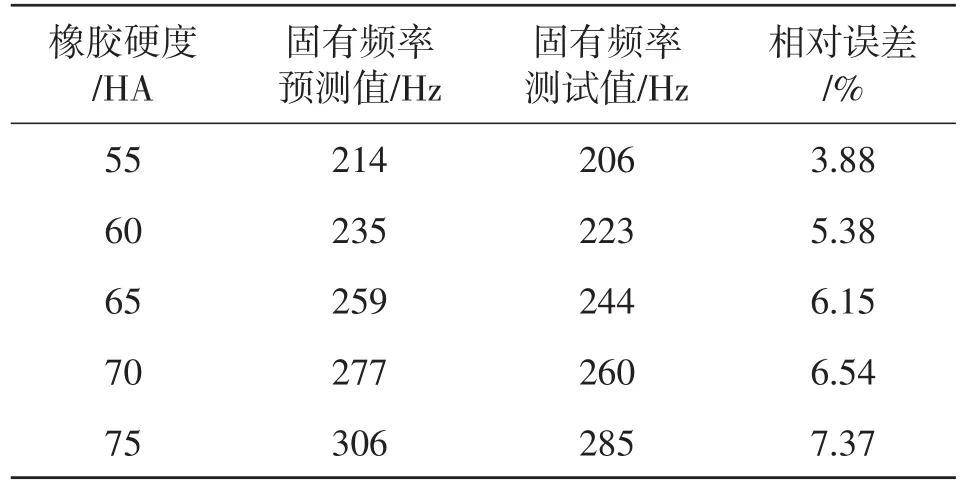
表5　不同橡胶硬度的扭转减振器固有频率预测值

表6　不同橡胶圈压缩比的扭转减振器固有频率预测值

由表5～6可知：橡胶扭转减振器固有频率的有限元预测值和实际测试值较为接近，相对误差均在8%以内；固有频率有限元预测值和实际测试值的变化趋势一致，固有频率随橡胶硬度的增加而变大、随橡胶圈压缩比的增加而变大。

5　结论

在橡胶扭转减振器固有频率测试方法的基础上，提出了基于ABAQUS软件的固有频率预测方法，并将有限元预测结果同试验结果进行了对比。1）对橡胶材料的超弹性本构模型和黏弹性本构模型进行了试验研究，结果表明：Mooney-Rivlin本构模型能较好描述橡胶圈橡胶材料的超弹性特性，当阶数N为3时Prony级数本构方程能较好地描述橡胶试件橡胶材料的黏弹性特性。2）橡胶扭转减振器固有频率有限元预测值和测试值的变化趋势一致，相对误差均在8%以内，且固有频率随橡胶硬度增加而变大、随橡胶圈压缩比增加而变大。3）采用本文中的有限元方法能在橡胶扭转减振器物理样机出来之前能对其固有频率进行准确预测，具有较强的工程应用价值。

［1］Szenasi F R.Analysis of Torsional Vibrations in Rotating Machinery［C］//Proceeding of the 22nd Turbomachinery Symposium.Dallas，TX，Sept.1993：14-16.

［2］张芳，王必璠，李显戴.车用发动机扭转振动的分析与控制［J］.汽车科技，2011（2）：47-51.

［3］Sharma，Renu.Characterization of the Molding Process of Passive Vibration Isolators［J］.Biological Chemistry，2012，48（3）：187-194.

［4］上官文斌，魏玉明，赵旭，等.橡胶阻尼式扭转减振器固有频率计算与测试方法的研究［J］.振动工程学报，2015（4）：550-559.

［5］Tarrago Garcia M J，Kari L.Frequency and Amplitude Dependence of the Axial and Radial Stiffness of Carbonblack Filled Rubber Bushings［J］.Polymer Testing，2007，26：629-638.

［6］上官文斌，陈超，段小成，等.发动机曲轴系统扭转振动建模与实测分析［J］.振动、测试与诊断，2012，32（4）：560-567.

［7］Parikyan T.Multi-Cycle Torsional Vibration Simulation With AVL EXCITE Designer［C］//ASME 2011 Internal Combustion Engine Division Fall Technical Conference. 2011：1009-1018.

［8］Lakshminarayanan P A，Stephen S，Dani A D，et al.Design and Development of a Torsional Vibration Rubber Damper［C］//SAE Technical Paper，990023.

［9］江丙云，孔祥宏，罗元元.ABAQUS工程实例详解［M］.北京：人民邮电出版社，2014.

［10］ABAQUS Inc.ABAQUS Analysis User's Manual［M］. Version 6.12，2010.

［11］胡小玲，刘秀，李明，等.炭黑填充橡胶超弹性本构模型的选取策略［J］.工程力学，2014（5）：34-42.

［12］Charlton D J，Yang J，Teh K K.A Review of Methods to Characterize Rubber Elastic Behavior for Use in Finite Element Analysis［J］.Rubber Chemistry and Technology，1994，67（3）：481-503.

［13］Li M，Hu X L，Luo W B，et al.Comparison of Two Hyperelastic Models for Carbon Black Filled Rubber［J］.Applied Mechanics&Materials，2013，275-277：28-32.

［14］魏玉明.橡胶阻尼式扭转减振器性能计算与测试方法的研究［D］.广州：华南理工大学，2014.

［15］Mats Berg.A Rubber Spring Model for Dunamic Analysis of Rail Vehicles［R］.report 1995：53，Division of Railway Technology，Department of Vehicle Engineering，Kuangl Tekniska Hogskolan，Stockholm，1995.

Study on Natural Frequency Prediction Method of Rubber-type Torsional Vibration Damper Based on ABAQUS

Guo Yiming1，2，Du Xiaoze2，Shangguan Wenbin2
（1.Hubei Key Laboratory of Automotive Power Train and Electronic Control，Hubei University of Automotive Technology，Shiyan 442002，China；2.School of Mechanical and Automotive Engineering，South China University of Technology，Guangzhou 510641，China）

The natural frequency prediction method using ABAQUS software was proposed based on the test method of natural frequency of the rubber-type torsional vibration damper.The constitutive model of theviscoelasticmaterialandtherubberhyper-elasticconstitutivemodelwerestudied.Takingtherubbertype torsional vibration damper circular drum type wheel hub as an example，the realization of the natural frequency finite element prediction method was introduced，and the results of the natural frequency simulation were compared with the test results of the natural frequency.The results show that the finite element methodproposedinthispapercanaccuratelypredictthenaturalfrequencyoftherubber-typetorsionalvibrationdamperbeforethephysicalprototype，whichhasastrongengineeringapplicationvalue.

rubber-typetorsionalvibrationdamper；naturalfrequency；predictionmethod；ABAQUS

U464.133+.3

A

1008-5483（2016）03-0005-06

10.3969/j.issn.1008-5483.2016.03.002

2016-07-05

汽车动力传动传动与电子控制湖北省重点实验室开放基金项目（ZDK201106）；湖北省教育厅科学技术研究项目（Q20122306）；十堰市科学技术研究与开发项目（20110272）

郭一鸣（1978-），男，湖北云梦人，副教授，从事汽车设计方法与理论、汽车振动分析与控制等方面的研究。E-mail：gym9643@163.com