时差定位精度影响因素分析
中国船舶重工集团公司第七二三研究所 袁鹏鹏
时差定位精度影响因素分析
中国船舶重工集团公司第七二三研究所袁鹏鹏
无源定位系统因其具有极强的隐蔽性、抗干扰能力,作用距离远,定位精度高等优点,在当代电子战中的地位越来越重要,受到世界各国的普遍重视。时差定位法具有对接收系统要求低、布站机动性强、定位精度高等显著特征,近年来成为无源定位系统中应用最为广泛的一种定位技术。本文分析了时差定位的基本原理,采用几何精度因子(GDOP)分析了影响时差定位性能的因素,仿真了几种不同几何布站下的等GDOP图,在实验室环境下建立了几种时差定位的模型,通过对比得到定位精度影响因素的分析结果。
无源定位;时差定位;GDOP
引言
在当代电子对抗的先进背景下,有源雷达系统容易被干扰和攻击。相比较而言,电子支援措施(ESM)定位跟踪技术能够远距离搜索、发现、定位、分析敌方目标,具有隐蔽性强、精度高、抗干扰能力强等特点,探测系统的生存能力和作战水平得到提高。多站无源定位技术跟踪精度高、定位效率高、定位速度快、获取信息量大、信息准确性高的优势相对于单站无源定位系统更加明显,这也预示其将在电子战中得到更大范围的运用[1]。时差测量定位法具有对接收系统要求不高、布站机动性强、定位精准度高等显著特征,因此近年来得到越来越多的重视和关注,成为无源定位系统中应用最为广泛的一种定位技术。
1.时差定位基本原理
时差定位系统一般由一个主站和两个或两个以上副站组成,以三站定位系统为例,其定位原理如图2-1所示[2]。
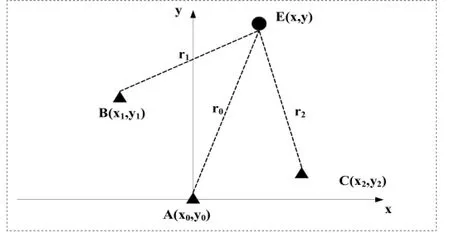
图2-1 时差定位原理示意图
如图所示,E(x,y)为辐射源目标位置,A(x0,y0)为主站位置,B(x1,y1)、C(x2,y2)分别为两个副站位置,r0、r1、r2分别为目标到主站A、副站B和C的距离。副站与主站的距离差分别为Δri(i=1,2),定位方程表示为:
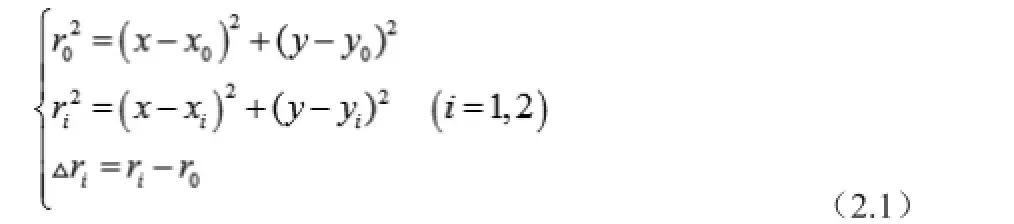
而:

其中,c=3×108m/s为电磁波传播速度,Δti(i=1,2)为副站与主站的时间差,t0、t1、t2分别为目标到主站A、副站B和C的时间。
时差定位精度分析
对式(2.2)两边求微分,可得:
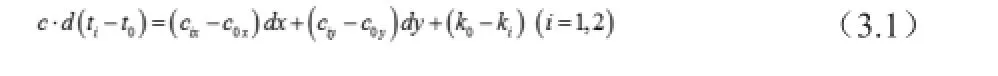
其中:

辐射源与观察站位置的相关系数矩阵可表示为:

可得dY=C·dX+dXS,用伪逆法求得的目标定位误差的估计值为:

令:

时间差的测量值中都包括目标到达主站的时间误差,因此各时差的测量值中都包含相同误差因子,所以目标到达各站的时差Δt的误差是相关的。假设时差修正后是零均值的,且各站址误差是相互独立的,则定位误差的协方差可表示为:

可得:
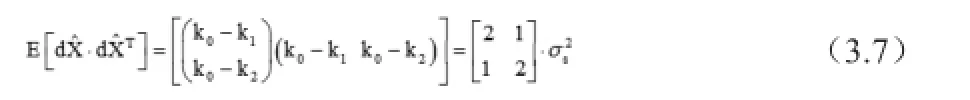
令:
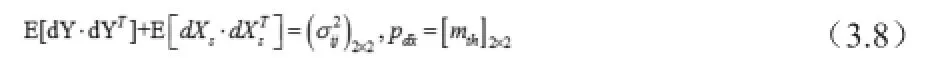
其中:
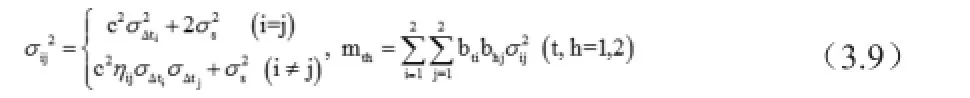
可到:

所以得到二维时差定位的定位精度为:

时差定位精度仿真由式(3.11)可知,定位精度与观察站布局、观察站位置测量误差、时间测量误差等因素有关。对于确定的布站形式,时差定位的精度主要取决于时间测量精度以及基线长度。对于三站直线型及三角型分布,分别按不同基线长度与站址误差,通过仿真计算,给出不同系统测时差误差情况下的GDOP分布,如图4-1、4-2所示。
时差定位精度试验分析在实验室环境下,利用三个固定站对运动辐射源进行时差定位,设定以下的几类场景,对三站时差定位精度的影响因素进一步验证、分析、总结规律:
a)对于基线10km直线型布站场景,目标从距离200km向主站的方向移动,对这一过程的定位数据进行统计、分析,见图5-1。
b)三站直线型布站,目标从距离200km向主站的方向移动,基线长度分别设为10km、20km、30km,测试三次,对目标的定位精度数据统计、分析如图5-2。
c)设置一个基线20km,三站直线布站,对起始位置距离主站200km的目标进行定位,随着目标距离主站不断接近,记录定位数据。场景重演三次,每次设置不同站址误差分别为10m、30m、50m,对三次的定位结果进行统计,内场实测数据统计分析见图5-3。
d)对(a)基线长度20km,直线布站时,(b)基线20km,三角形布站时,目标距离主站分别为约120km附近围绕主站作圆弧形运动,验证目标相对主站不同方位下的定位精度,见图5-4和图5-5。
实测数据表明:
1)其他因素一定的情况下,目标距离站点距离越近定位精度越高;
2)其他因素一定的情况下,基线越长定位精度越高;
3)其他因素一定的情况下,站址误差越小定位精度越高;
4)目标距离站点位置一定的情况下相对站点不同方位,定位精度不同,定位站采用对称结构布置,定位精度相对较高,目标辐射源在定位站基线中垂线上移动时,定位精度最高。当目标辐射源在定位站基线或其延长线上时,定位误差最大。

图4-1 直线型布站情况下的定位精度分布图
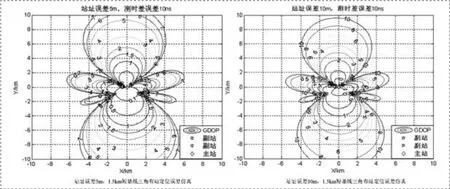
图4-2 三角型布站情况下的定位精度分布图
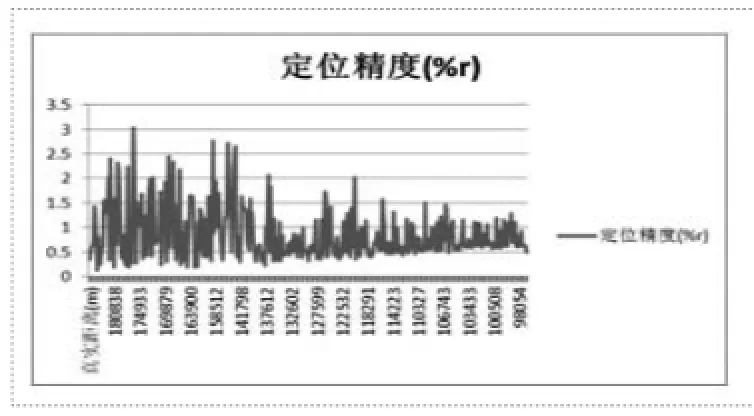
图5-1 基线10km直线型布站情况下的定位精度

图5-2 不同基线时站址误差情况下的定位误差

图5-4 线型布站目标围绕站点运动时不同方位定位精度图
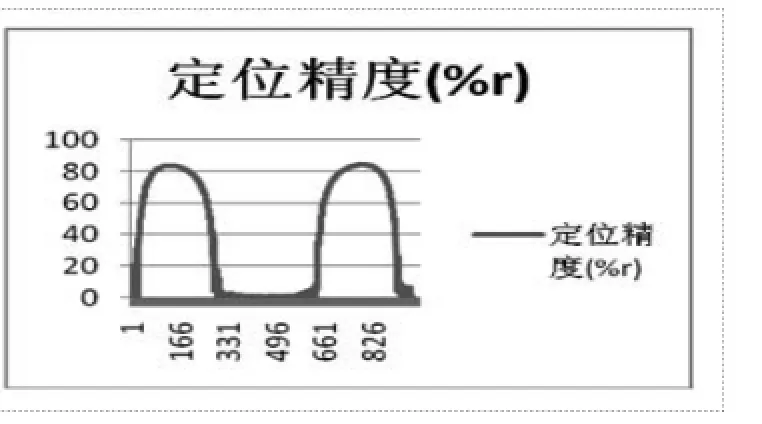
图5-5 三角形布站目标围绕站点运动时不同方位的定位精度
2.结束语
通过仿真分析以及实验室测试数据统计、分析可以看出,定位精度与定位站布局、站址误差、时间测量误差、基线长度等因素有关。并且时差测量值、站址误差增大,定位误差随之增大;定位误差随目标至定位站距离增大而增大,距离较远时,误差增加较快;目标与定位站相对位置,对定位精度影响较大。定位站成等腰三角形分布,目标在等腰三角形底边中垂线
上,定位误差较小;当目标在定位站基线或其延长线上时,定位误差无穷大;定位站之间的距离越大,定位精度越高,但在实际布站中,基线长度又受到站间通信、时差测量误差的制约。
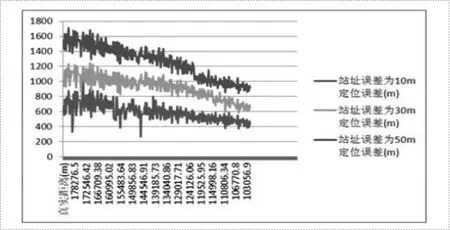
图5-3 基线为20km时不同站址误差情况下的定位误差
[1]赵国庆.雷达对抗原理[M].西安电子科技大学出版社,1999.
[2]冯富强,张海彦,陈永光.基于实验数据的时差定位系统定位精度推算[J]. 现代雷达,2005,12:11-13,28.
袁鹏鹏,大学本科,助理工程师,现供职于中国船舶重工集团公司第七二三研究所。

