一种装配式塑料模板的刚度、强度性能试验

林林　　郑焕奇　　陈启文　　唐黎　　冼汉光　　费飞龙，2

（1广东省建筑科学研究院集团股份有限公司 建筑材料研究所）

（2华南理工大学 材料学院）

（3广州毅昌模板工程有限公司）

一种装配式塑料模板的刚度、强度性能试验

林林1郑焕奇1陈启文1唐黎3冼汉光3费飞龙1，2

（1广东省建筑科学研究院集团股份有限公司 建筑材料研究所）

（2华南理工大学 材料学院）

（3广州毅昌模板工程有限公司）

本文研究了在模板工程设计和施工实际受载情况的基础上，考虑最不利情况下的荷载情况，相应地计算出最不利荷载所对应的刚度荷载和强度荷载，采用静态荷载试验来对塑料模板进行加载，检测单块模板、龙骨模板及组合模板在各加荷级数下的挠度值和模板在受载整个过程中的破坏情况，从而分析刚度荷载和强度荷载作用下，塑料模板的挠度值以及卸载后的残余变形量，进而得出该模板设计是否安全。

塑料模版；强度；刚度；挠度值；承载能力

1　引言

塑料模板是一种适用于工程施工的模板工程，具有施工速度快，周转次数多，可全部回收等特点，节能减排，响应当下绿色环保的主题。近年来高层建筑增多，传统模板已不能满足实际工程的需求，模板工程的重要性日益突出。塑料模板是一种类似于铝合金模板的模板体系，根据设计要求，制作标准化单元，到工地拼装即可浇筑，耗时较使用传统模板大大缩短，提高工程的经济效益。同时，塑料模板密封性好，成型后的混凝土表面较为致密，有益于混凝土的耐久性能。鉴于塑料模板的优点，其在工程应用有较好的前景。

随着高层与大跨度混凝土构件的日益增多，因支撑体系失稳造成模板坍塌的事故屡见不鲜，严重影响了人员安全和工程进度。为了在建筑工程中的应用推广，塑料模板体系安全评价显得尤为重要，并成为其推广应用过程中的一项基础性研究工作。本文在计算最不利荷载组合的基础上，采用静态荷载试验来模拟塑料模板在工程应用的受载情况，从而评价其在实际工程中是否安全。

2　试验材料与方法

2.1原材料与仪器

实验所用塑料模板为广州某模板工程有限公司提供规格为1000×500（型号88）、250×200（型号43）、200×200（型号33）的面板模板和1000×200的龙骨模板。

主要试验仪器为：万能压力机、支座、百分表、砝码（标定过的钢锭）、卷尺等。

2.2试验方法

本文根据理论计算确定最不利刚度和强度的荷载，采用静态荷载试验对塑料模板施加最不利荷载，测试该荷载作用挠度值，来分析塑料模板的刚度和强度。挠度值是材料在所受外力情况下不致影响使用功能时产生的最大弯曲变形值的数值。塑料模板弯曲变形时其横截面形心沿与轴线垂直方向的线位移即为挠度值。

模拟单块模板、龙骨模板和组合模板工程实际受载情况，采用均布荷载逐级加荷的方式，来获得各加荷级数的挠度值及破坏情况。

2.2.1单块模板、龙骨模板挠度试验方法

单块模板的试验方法是将试件安放在支撑间距800mm的支座上，受荷载情况如图1；在试件支点之间1/2，且离试件边缘10mm处，各安放一块百分表；在试件上施加0.1～0.2kN的预加荷载，将百分表调整到“零”位；按表1进行逐级加荷，并记录每级加荷后百分表的读数，取算术平均值，计算最大挠度及残余变形值，卸载后检查并记录试件破坏情况。取三块试件做平行试验。

图1　单块模板（或龙骨模板）均布荷载示意图

龙骨模板的试验可以参照单块模板的试验方法，按照单块模板的方式安放好试件，试件受荷载示意图如图1；不同的是龙骨模板试验的加荷顺序和恒载时间与单块模板试验有所不同，见表1。

2.2.2组合四块模板挠度试验方法

组合四块模板的试验方法是将六块模板（其中左右两边的两块型号33模板面起固定作用）短边拼接，安放在间距700mm的四个早拆头支座上，受荷载情况如图2；在试件支点之间1/2及试件宽度的1/2处，安放一块百分表；在试件上施加0.1～0.2kN的预加荷载，将百分表调整到“零”位；按表1进行逐级加荷，并记录每级加荷后百分表的读数，取算术平均值，计算最大挠度及残余变形值；卸载后检查并记录试件破坏情况。取三块试件做平行试验。

图2　组合四块模板均布荷载示意图

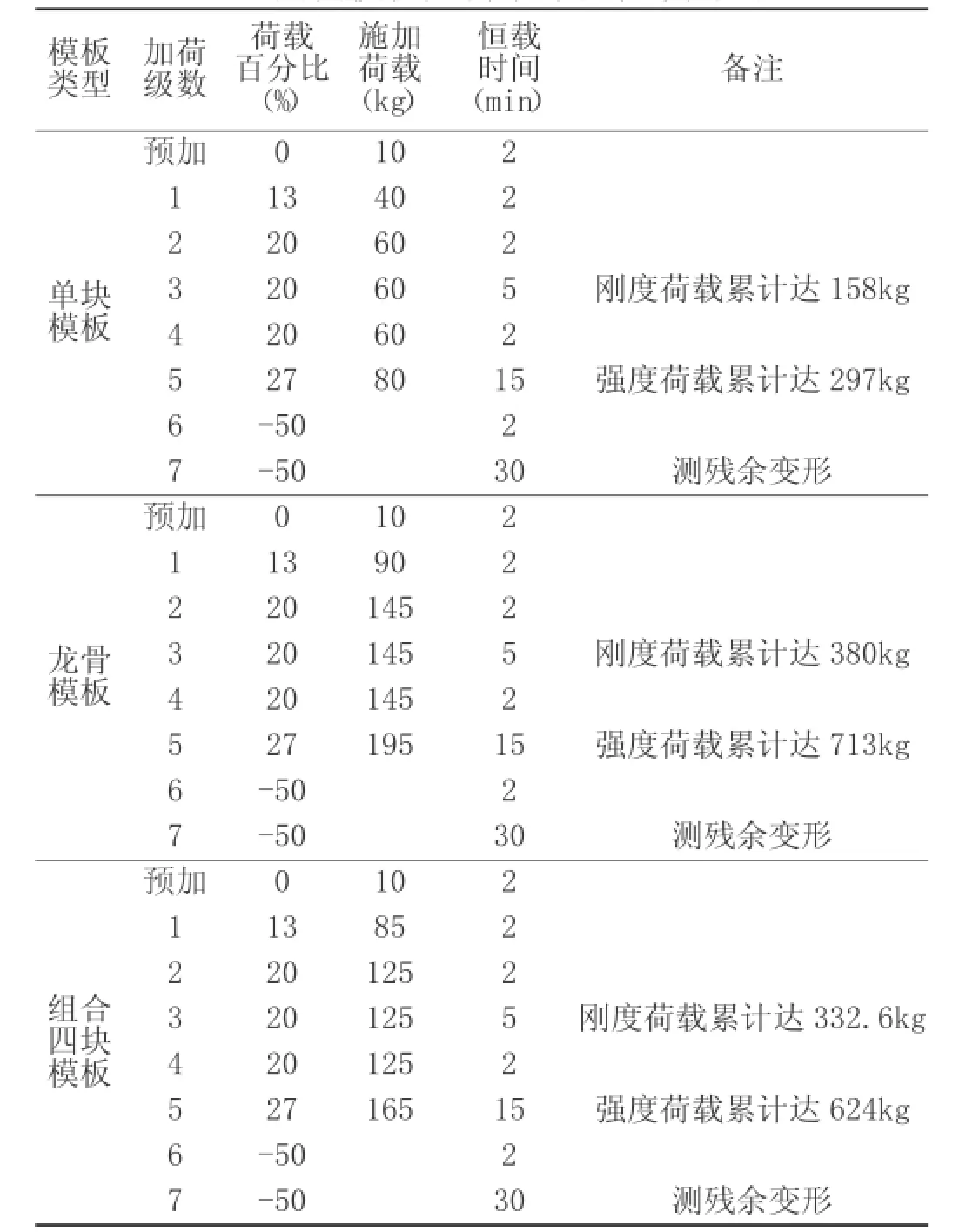
表1　单块模板、龙骨模板、组合四块模板加荷顺序及恒载时间

3　计算与结果分析

3.1载荷计算与分析

根据浇筑混凝土的实际情况和JGJ 162-2008《建筑施工模板安全技术规范》，本文通过考虑对刚度和强度最不利的荷载，采用静态荷载试验，将该最不利荷载作用在试件上，测试挠度值和观察破坏情况，分析试件在该荷载作用下塑料模板是否能满足实际工程要求，从而评价其在工程应用的安全。

3.1.1模板的荷载和荷载设计值

考虑到塑料模板尚未广泛运用于实际工程中，本文以浇筑厚度为0.15m的普通混凝土楼板为例。

永久荷载标准值按规定取值如下，由于规范中没有塑料模板自重，按塑料模板和支架的实际自重，采用塑料模板及其支架自重标准值G1=0.2kN/m2；浇筑普通混凝土楼板时混凝土自重可取24kN/m3，新浇筑混凝土自重标准值G2=24×0.15=3.6kN/m2；浇筑楼板用钢量可取1.1kN/m3，钢筋自重标准值G3=1.1×0.15=0.165kN/m2，因此，楼板永久荷载标准值为G1+G2+G3=3.965kN/m2。

可变荷载标准值按规定取值如下，可取施工人员及设备荷载标准值Q1=2.5kN/m2；暂不考虑风荷载，因此，楼板可变荷载标准值为Q1=2.5kN/m2。

按极限状态设计时，模板荷载组合可从由可变荷载效应控制或由永久荷载效应控制的基本组合中，选取最不利的组合作为荷载效应组合的设计值。

由可变荷载效应控制的基本组合为：

S1=r0×［γG×（G1+G2+G3）+γQ×Q1］=0.9×［1.2×（0.2+24×0.15+1.1×0.15）+1.4×2.5］=7.43kN/m2

式中：

S1——由可变荷载效应控制的基本组合；

G1——塑料模板及其支架自重标准值（kN/m2）；

G2——新浇筑混凝土自重标准值（kN/m2）；

G3——钢筋自重标准值（kN/m2）；

Q1——钢筋自重标准值（kN/m2）；

r0——结构重要性系数，按规定可取值0.9；

γG——永久荷载分项系数，按规定可取值1.2；

γQ——可变荷载分项系数，按规定可取值1.4。

由永久荷载效应控制的基本组合为：

S2=r0×［γG×（G1+G2+G3）+γQ×ψ ×Q1］=0.9×［1.35×（0.2+24×0.15+1.1×0.7×0.15）+1.4×2.5］=7.02kN/m2

式中：

S2——由永久荷载效应控制的基本组合；

ψ——可变荷载的组合系数，数值为0.7；

γG——永久荷载分项系数，按规定可取值1.35；

γQ——可变荷载分项系数，按规定可取值1.4。

G1、G2、G3、Q1、r0的意义如前文所述。

因为 S1＞S2，故荷载效应组合的设计值应采用S=S1=7.43kN/m2。

3.1.2刚度计算与分析

以文中提到的单块模板为例，该模板的型号是88，规格是 1000×500，试验跨度 800mm，根据 JGJ 162-2008，由3.1.1可得刚度验算用的荷载标准值为G1+G2+G3=3.965kN/m2，不考虑施工人员及设备荷载作用，因此，单块模板在最不利刚度情况时的刚度荷载：

N1=（G1+G2+G3）×A1=3.965×0.5×0.8=1.586kN式中，

G1——塑料模板及其支架自重标准值（kN/m2）；

G2——新浇筑混凝土自重标准值（kN/m2）；

G3——钢筋自重标准值（kN/m2）；

Q1——施工人员及设备荷载标准值（kN/m2）；

N1——单块模板在最不利刚度情况时的刚度荷载（kN）；

A1——单块模板实际承受荷载面积。

同理，可得龙骨模板（规格为1000×200，试验跨度800m）在最不利刚度情况时的刚度荷载：

N2=3.96×0.2×0.8+3.96×0.8×0.5×2=3.802kN

式中，N2——龙骨模板在最不利刚度情况时的刚度荷载（kN）。

同理，可得组合四块模板（该试件由1000×500型号88、250×200型号43、200×200型号33组成，试验跨度700mm）在最不利刚度情况时的刚度荷载：

N3=3.96×0.2×0.7+3.96×0.5×0.7×2=3.326kN

式中，N3——组合四块模板在最不利刚度情况时的刚度荷载（kN）。

将所得的刚度荷载加载到模板试件上，得出的相应变形量即挠度值，与现有模板要求的变形量做比较，判断模板在该刚度荷载作用下能否安全。

3.1.3强度计算与分析

以文中提到的单块模板为例，该模板的型号是88，规格是 1000×500，试验跨度 800mm，根据 JGJ 162-2008，由3.1.1可得刚度验算用的荷载效应组合设计值为S=7.43kN/m2，因此，单块模板在最不利强度情况时的强度荷载：

Na=S×Aa=7.43×0.5×0.8=2.97kN

式中：

S——荷载效应组合设计值（kN/m2）；

Na——单块模板在最不利强度情况时的强度荷载（kN）；

Aa——单块模板实际承受荷载面积。

同理，可得龙骨模板（规格1000×200，试验跨度800mm）在最不利强度情况时的强度荷载：

Nb=7.43×0.2×0.8+7.43×0.8×0.5×2=7.13kN

式中，Nb——龙骨模板在最不利强度情况时的强度荷载（kN）。

同理，可得组合四块模板（该试件由1000×500型号88、250×200型号43、200×200型号33组成，试验跨度700mm）在最不利强度情况时的强度荷载：

Nc=7.43×0.2×0.7+7.43×0.5×0.7×2=6.24kN

式中，Nc——组合四块模板在最不利强度情况时的强度荷载（kN）。

将所得的强度荷载加载到模板试件上，得出的相应变形量，与现有模板要求的变形量做比较，判断模板在该强度荷载作用下能否安全。

3.2试验结果与分析

表2　单块模板、龙骨模板、组合四块模板试验检测数据

图3　各类型模板加荷挠度值曲线

3.2.1单块模板试验结果与分析

单块模板的试验检测数据见表2，其逐级加荷曲线见图3。从加荷级数1至加荷级数5，随荷载增加，挠度值呈现平稳上升，且挠度值变化有加快的趋势；当加载至加荷级数5时，累积荷载达到最大值，即强度荷载，其数值为297kg，对应的挠度值为3.042mm；从加荷级数5至加荷级数7，随荷载减少至预加载的荷载，挠度值平稳减小，试件均未出现破坏的情况，残余变形值为0.010mm。

3.2.2龙骨模板试验结果与分析

龙骨模板的试验检测数据见表2，其逐级加荷曲线见图3。从加荷级数1至加荷级数5，随荷载增加，挠度值呈现平稳上升，且挠度值变化有减缓的趋势；加载至加荷级数5时，累积荷载达到强度荷载，其数值为713kg，对应的挠度值为4.246mm；从加荷级数5至加荷级数7，随荷载减少至预加载的荷载，挠度值平稳减小，试件均未出现破坏的情况，残余变形值为0.230mm。

3.2.3组合四块模板试验结果与分析

组合四块模板的试验检测数据见表2，其逐级加荷曲线见图3。从加荷级数1至加荷级数3，随荷载增加，挠度值呈现缓和上升；在加荷级数2-6时，试件中型号43塑料模板间拼接处均出现肉眼可见缝隙；加载至加荷级数5时，累积荷载达到强度荷载，其数值为624kg，对应的挠度值为13.423mm；从加荷级数5至加荷级数6，随荷载减少，挠度值缓和减少；从加荷级数6至加荷级数7，随着荷载减少至预加载荷载，挠度值减少加显较快，试件均未出现破坏的情况，残余变形值为0.009mm。

综合以上几种类型模板试件分析，从加荷级数1至加荷级数5，再从加荷级数5至加荷级数7，组合四块模板的挠度值变化的幅度和程度较单块模板和龙骨模板显著，其数值约为单块模板的4倍，龙骨模板的3倍；加荷级数5时，组合四块模板的强度荷载比龙骨模板小，但其最大挠度值明显大于龙骨模板和单块模板的最大挠度值，说明随着组合模板的强度较单一块模板的差。加荷级数7时，单块模板和组合四块模板的残余变形值可以忽略不计，但龙骨模板的残余变形值是较为显著。

4　结论

本研究通过对单块模板、龙骨模板和组合四块模板等几种类型的塑料模板做基础性的试验检测，初步探索得到结论如下：

⑴本文在模板工程设计和施工实际受载情况的基础上，考虑最不利情况下的荷载情况，计算出该最不利荷载情况所对应的挠度荷载和强度荷载，采用静态荷载试验对塑料模板进行加载，检测模板在各加荷级数下的挠度值和受载过程中的破坏情况，分析刚度荷载和强度荷载作用下挠度值以及残余变形量，来评价模板设计是否安全。本文研究的试验检测方法在实际的操作是简便可行的，更贴近工程实际需求，但鉴于目前数据积累较少，需在今后逐步完善，更好更快地应用于工程中。

⑵从龙骨模板和组合四块模板的试验检测情况来，单一块模板的强度较高，但其残余变形情况不如组合模板好，由于塑料模板的特点在于板与板之间通过快接件连接在一起，形成较好的受力条件，但对于组合模板需要增加支撑杆件。为了让这种检测方式更适用于塑料模板，在试验中更加准确模拟出更多组合模板的拼接情况是下一步研究的重点。●

［1］JGJ 162-2008建筑施工模板安全技术规范［S］.

［2］张良杰.早拆模板施工技术及新型水平模板支撑系统应用［J］.施工技术，2014，（5）：24-28.