基于时变ARMA和EMD-PSO-LSSVM算法的非平稳下击暴流风速预测

李春祥,迟恩楠,何　亮,李正农

(1.上海大学 土木工程系,上海　200072；2.湖南大学 土木工程学院,长沙　410082)



基于时变ARMA和EMD-PSO-LSSVM算法的非平稳下击暴流风速预测

李春祥1,迟恩楠1,何亮1,李正农2

(1.上海大学 土木工程系,上海200072；2.湖南大学 土木工程学院,长沙410082)

根据非平稳过程的进化谱理论，导出基于TARMA模型的非平稳脉动风速模拟式。基于模拟解析式，得到一些空间点非平稳下击暴流风速的模拟时间序列；运用经验模式分解(EMD)和基于粒子群优化(PSO)的最小二乘支持向量机(LSSVM)(简称为PSO-LSSVM)算法，经MATLAB平台编制程序，根据上下空间点风速样本预测出中间高度处的非平稳下击暴流风速时程。通过功率谱、自相关和互相关函数预测值与模拟值的比较及平均误差(AE)、均方根误差(MSE)和相关系数(R)的评价，验证了基于时变ARMA模型和EMD-PSO-LSSVM算法的下击暴流风速模拟与预测的可行性。

下击暴流；预测；时变ARMA；经验模式分解；最小二乘支持向量机

下击暴流为雷暴天气中强烈的下沉气流猛烈撞击地面，并由撞击点向四周沿地表传播的极具突发性和破坏性的一种强风。由下击暴流引发的结构破坏在世界各地都有发生，近年来已经引起了工程界与科研界的广泛注意。根据有关机构的记录，在美国、澳大利亚、南非等地，大约80%与气候相关的输电塔破坏是由下击暴流或龙卷风这类高强风所引起的[1]。国外学者对下击暴流进行了数次实测，发现下击暴流的风速竖向分布与传统大气边界层风速分布有很大的不同[2]，下击暴流最大风速位置比较接近地表，离地表较远处风速相对较小。雷暴的平移速度对下击暴流风速有较大的影响，大约占平均风速的三分之一。下击暴流风速具有很强的非平稳性和强的相关性较，可能会引起结构更大的动力响应。许多学者对下击暴流进行了研究[3-8]。WANG等[9]基于实测记录提出了使用小波和希尔伯特模拟下击暴流风速。然而，目前有关非平稳下击暴流风速的预测报道很少。本文在提出适用于模拟非平稳下击暴流风速的时变ARMA模型基础上，发展其EMD-PSO-LSSVM预测算法。

1　非平稳风速模拟的时变ARMA模型及流程

设M点非平稳脉动风速为：

U(t)=[u1(t)u2(t)…uM(t)]T

(1)

于是，其时变ARMA模型可表示为：

(2)

为模拟计算U(t)，关键要确定Ai(t)和Bj(t)系数矩阵。当t=t0时，式(2)变为：

(3)

对式(3)两边同时右乘UT(t0-kΔt)(k=1,2,…，p)，并取数学期望得到：

E[U(t0)UT(t0-kΔt)]=

(4)

根据相关函数定义：

(5)

再对(3)两边同时右乘XT(t0-lΔt)(l=1,2,…，q)，并取数学期望得到式(6)或式(7)。

E[U(t0)XT(t0-lΔt)]=

(6)

(7)

从式(3)可看出：当前输出U(t0)只依赖于当前输入X(t0)和过去输入X(t0-τ)，而与将来输入X(t0+τ)无关(τ>0)，即U(t0)与X(t0+τ)相互独立，则有Rux(-τ)=0,τ>0和Rux(-τ)=Rxu(τ)。当j=0时，k-j>0，则Rxu[(k-j)Δt]=0。式(5)和式(7)合并后展开得：

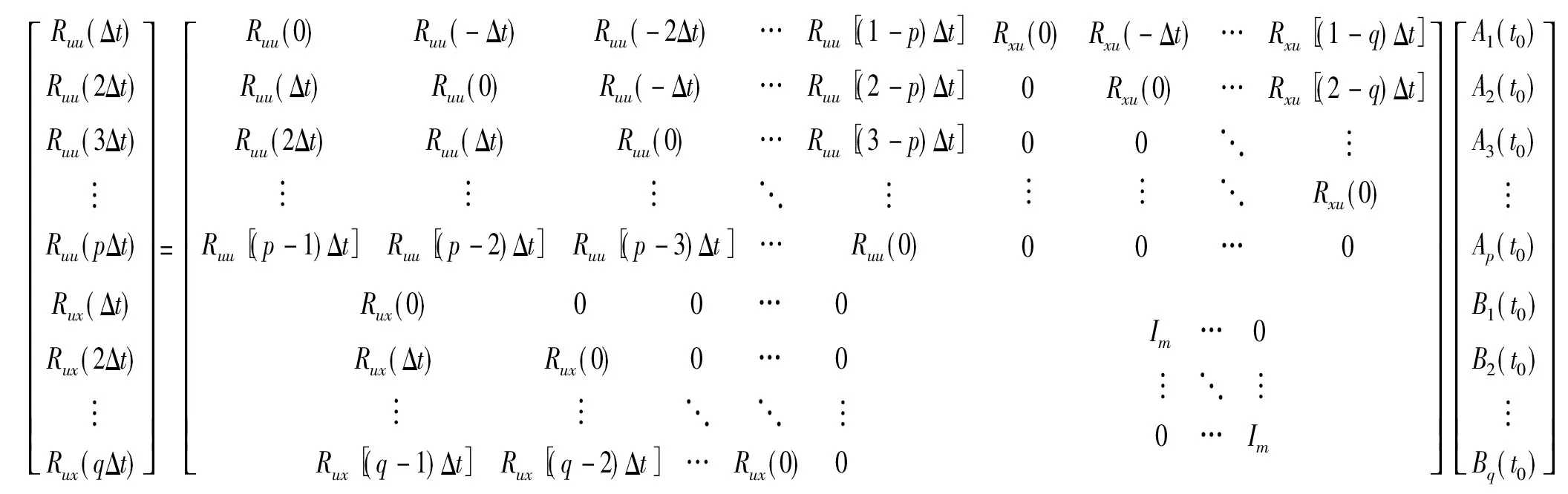
(8)

在式(8)中，

[Ruu(jΔt)]M×M=

根据维纳-辛钦公式

即可求出[Ruu(jΔt)]，此时，尚需已知[Rux(lΔt)]才能求得Ai(t)和Bj(t)系数矩阵。令式(3)中q=0，得到：

(9)

对式(9)两边同时右乘XT(t0-lΔt)以及两边同时右乘UT(t0-kΔt)，并分别取数学期望得到：

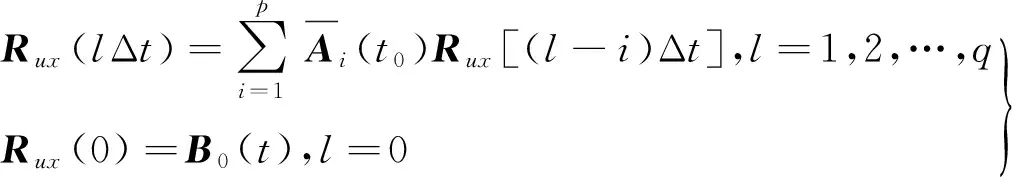
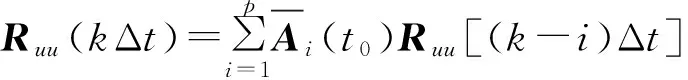
(12)

对式(13)右边进行Cholesky分解，即可求得B0(t0);再代入式(10)递推求得矩阵[Rux(lΔt)]。将矩阵[Ruu(jΔt)]和[Rux(lΔt)]代入式(8)，即可确定TARMA模型系数矩阵Ai(t)和Bj(t)，最终得到t0时刻的风速。图1给出了基于时变ARMA模型的非平稳脉动风速模拟流程图。

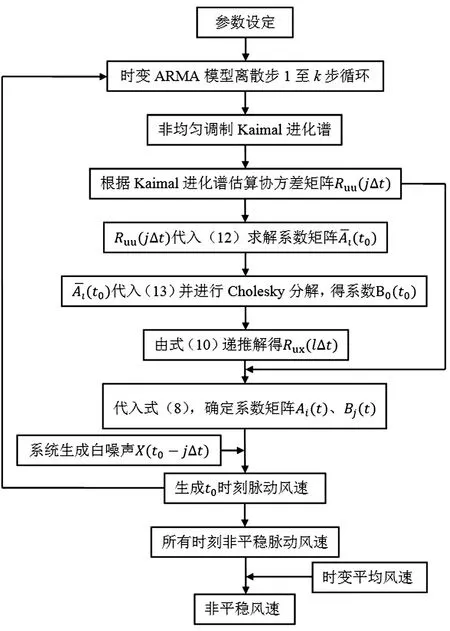
图1　基于TARMA模型的非平稳风速模拟流程Fig.1　Flowchart of TARMA model based nonstationary wind velocity simulation

2　基于TARMA模型的非平稳下击暴流风速模拟及验证

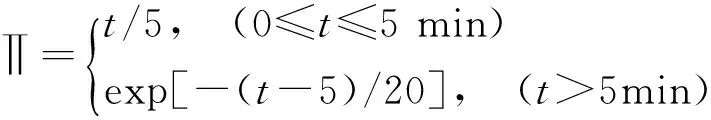
图2给出基于TARMA模型模拟出的10 m、30 m、50 m、70 m高度1 000 s非平稳风速时程。由图2知，脉动风速幅值与时变平均风速有关，时变平均风速越大则脉动风速越大，与实际风场特性吻合。进一步，计算了模拟的非平稳脉动风速功率谱(模拟谱)和模拟风速的自、互相关函数(模拟值)与非均匀调制的Kaimal进化谱(目标谱)和通过目标谱计算出的自、互相关函数(目标值)。经对比，发现模拟值与目标值吻合很好，再次表明该模型模拟的有效性。

3　基于EMD-LSSVM的非平稳下击暴流风速预测及验证

10 m、30 m、50 m、70 m高度的模拟非平稳风速时程作为输入，而20 m、40 m、60 m高度的非平稳风速时程作为输出。首先，对上下空间点非平稳风速进行EMD分解，分解为一系列相对平稳的分量；然后，采用游程判定法，将波动程度相近的分量分别重构为高、中、低频三个分量，对上下空间点的三个分量分别预测中间点的高、中、低频三个分量；接着，分别对高、中、低频分量采用PSO-LSSVM算法进行预测；最后，对中间点的三个预测分量进行叠加而得到最终的预测风速。图3给出了非平稳风速预测流程图。在PSO-LSSVM算法中，取2 000个时间点(1 000 s)的脉动风速作为样本，将这些样本数据分成两部分：前1 000个时间点(500 s)的数据作为学习训练样本，后1 000个时间点(500 s)的数据作为预测验证样本。

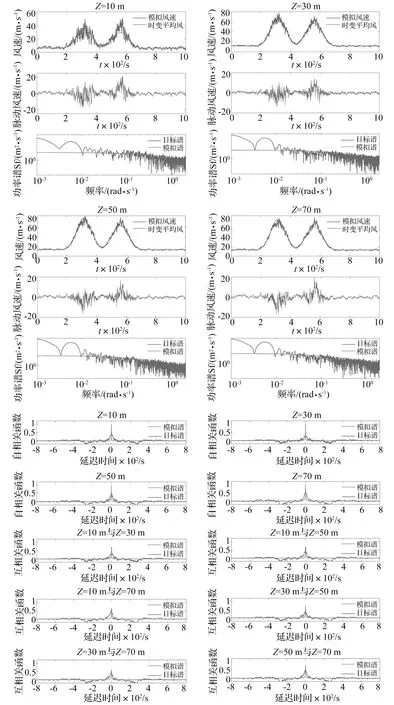
图2　使用TARMA模型模拟的非平稳下击暴流风速及验证Fig.2　Simulated nonstationary wind velocity using TARMA model as well as verification

图3　基于EMD-PSO-LSSVM的非平稳风速预测流程Fig.3　Flowchart of nonstationary wind velocity forecasting based on EMD-PSO-LSSVM

非平稳样本可以分解为少量固有模态函数(imf)。每个imf函数代表了数据中隐含的固有振荡模式。EMD方法通过筛分过程实现imf函数的分解。对10 m、30 m、50 m、70 m处风速分解产生有限个imf分量和剩余分量。在图4中，Signal为原始非平稳风速，imf1-imf9为分解后固有模态函数，res为筛分后余量很小或为单调函数的剩余分量。随后选用游程判别法对分解所得imf和剩余分量进行波动程度检验，将波动程度相近的分量分别重构为高、中、低频三个分量，使所得分量特征信息集中且预测分量大幅减少。

本文以0.5 s为风速时程的时间单位，样本数N=2 000，则选择n1=50作为高频分量的阈值(大于n1的为高频分量)，叠加作为高频分量R1；以剩余分量的游程数n2作为低频分量的阈值(小于等于n2的为低频分量)，作为低频分量R3；其余为中频分量，叠加作为中频分量R2。由此，非平稳风速时间序列被重构为频率从高到低排列的特征信息集中三个分量。图5给出非平稳脉动风速分类重构图，原始风速=R1+R2+R3。

图4　10 m、30 m、50 m、70 m高度的非平稳风速EMD分解Fig.4　EMD of nonstationary wind velocity at 10 m,30 m,50 m and 70 m

针对三个分量的特征，建立相应的PSO-LSSVM预测模型。参数设定为：种群规模M=40，进化次数为300次，加速因子c1=1.5，c2=1.7，初始惯性权重和最大进化惯性权重分别取wmax=0.9，wmin=0.4。最后，将三个分量的预测结果进行叠加作为最终的预测风速值，如图6所示。由图6知，不同高度脉动风速时程的预测值与目标值(模拟值)吻合程度很高，而且自相关和互相关函数的预测值与目标值基本一致。表1给出基于EMD-PSO-LSSVM的非平稳脉动风速预测性能评价指标。由表1知，EMD-PSO-LSSVM的平均误差和均方根误差很小，而且相关系数也比较大(认为相关系数R≥0.8时，具备很强的相关性)。因此，该预测算法具有良好的预测性能。

表1　EMD-PSO-LSSVM预测性能评价指标

图5　10 m、30 m、50 m、70 m高度非平稳风速重构Fig.5　Reconstruction of nonstationary wind velocity at 10 m,30 m,50 m,and 70 m

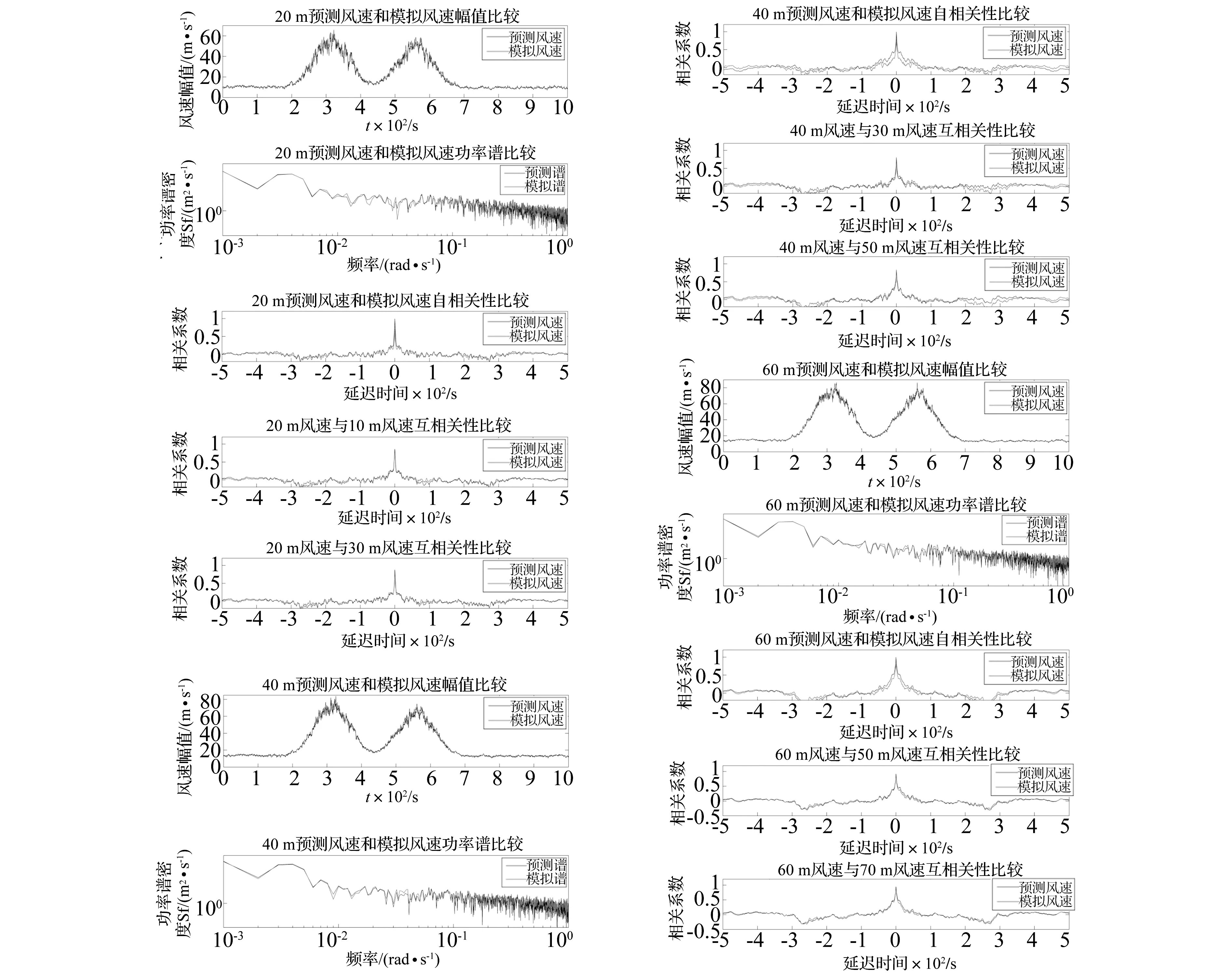
图6　基于EMD-LSSVM的非平稳下击暴流风速预测及验证Fig.6　Predicted nonstationary wind velocity using EMD-LSSVM as well as verification

非平稳风速时间序列经EMD处理后分解为若干相对平稳的分量，从而简化了不同特征信息之间的干涉和耦合，而且重构后所得三分量的特征信息集中且变化规律明显，进而能够有针对性地建立更为准确的预测模型，同时重构后分量大大减少，提高了预测模型的效率，可节约预测成本。

4　结　论

使用TARMA模型，对上下空间点的非平稳下击暴流风速进行数值模拟，并对其实行EMD分解，分解为一系列相对平稳的分量；然后，采用游程判定法，将波动程度相近的分量重构为高、中、低频三个分量，通过上下空间点的三个分量分别采用PSO-LSSVM算法预测中间点的高、中、低频三个分量，最后叠加得到中间点的最终预测风速。数值验证表明：不同高度处脉动风速时程的预测值与目标值(模拟值)吻合程度很高，自相关和互相关函数的预测值与目标值基本一致。根据EMD-PSO-LSSVM非平稳下击暴流风速的预测性能评价指标，发现EMD-PSO-LSSVM算法具有良好的预测性能。

[1]SAVORY E,PARKE GERARD A R,ZEINODDINI M,et al.Modelling of tornado and microburst-induced windloading and failure of a lattice transmission tower[J].Engineering Structures,2001,23(4):36-75.

[2]CHEN L,LETCHFORD C W.A deterministic-stochastic hybrid model of downbursts and its impact on a cantilever structure[J].Engineering Structures,2004,26(5):619-26.

[3]瞿伟廉,王锦文.下击暴流风荷载的数值模拟[J].武汉理工大学学报,2008,30(2):70-74.

QU Weilian,WANG Jinwen.Numerical simulation of downburst wind loads[J].Journal of Wuhan University Technology,2008,30(2):70-74.

[4]王昕,楼文娟,李宏男,等.雷暴冲击风作用下高耸输电塔风振响应[J].浙江大学学报(工学版),2009,43(8):1520-1525.

WANG Xin,LOU Wenjuan,LI Hongnan,et al.Wind-induced dynamic response of high-rise transmission tower under downburst wind load[J].Journal of Zhejiang University(Engineering Science),2009,43(8):1520-1525.

[5]李春祥,李锦华,于志强.输电塔线体系抗风设计理论与发展[J].振动与冲击,2009,28(10):15- 25.

LI Chunxiang,LI Jinhua,YU Zhiqiang.A review of wind-resistant design theories of transmission tower-line systems[J].Journal of Vibration and Shock,2009,28(10):15-25.

[6]李春祥,刘晨哲,申建红,等.土木工程下击暴流风速数值模拟的研究[J].振动与冲击,2010，29(10):49-54.

LI Chunxiang,LIU Chenzhe,SHEN Jianhong,et al.Numerical simulations of downburst wind speeds in civil engineering[J].Journal of Vibration and Shock,2010,29(10):49-54.

[7]张文福,谢丹,刘迎春,等.下击暴流空间相关性风场模拟[J].振动与冲击,2013，32(10):12-16.

ZHANG Wenfu,XIE Dan,LIU Yingchun,et al.Simulation of downburst wind field with spatial correlation[J].Journal of Vibration and Shock,2013,32(10):12-16.

[8]李锦华,吴春鹏,陈水生.下击暴流非平稳脉动风速数值模拟[J].振动与冲击,2014,33(14):54-60.

LI Jinhua,WU Chunpeng,CHEN Shuisheng.Simulation of non-stationary fluctuating wind velocity in downburst[J].Journal of Vibration and Shock,2014,33(14):54-60.

[9]WANG Lijuan,MCCULLOUGH M,KAREEM A.A data-driven approach for simulation of full-scale downburst wind speeds[J].Journal of Wind Engineering and Industrial Aerodynamics,2013,123:171-190.

[10]LI Jinhua,LI Chunxiang,HE Liang,et al.Extended modulating functions for simulation of wind velocities with weak and strong nonstationarity[J].Renewable Energy,2015,83:384-397.

Prediction of nonstationary downburst wind velocity based on time-varying ARMA and EMD-PSO-LSSVM algorithms

LI Chunxiang1,CHI Ennan1,HE Liang1,LI Zhengnong2

(1.Department of Civil Engineering,Shanghai University,Shanghai 200072,China；2.School of Civil Engineering,Hunan University,Hunan 410082,China)

Using the theory of evolutionary power spectral density for nonstationary processes,the formula of the time-varying auto regressive moving average (TARMA)model was derived to simulate nonstationary downburst wind velocity.The simulation of nonstationary downburst wind velocity time histories at some space points was conducted using TARMA.Adopting the empirical mode decomposition (EMD)and the particle swarm optimization (PSO)based least squares support vector machines (LSSVM)making a programming with MATLAB,the prediction of nonstationary downburst wind velocity time histories at middle space points was accomplished using the nonstationary downburst wind velocity samples at upper and lower two space points.Through comparing the simulated values and the predicted ones of the power spectrum,autocorrelation and cross-correlation functions,respectively,it was shown that the TARMA and EMD-PSO-LSSVM algorithm-based simulation and prediction are feasible for nonstationary downburst wind velocity.

downbursts; prediction; time-varying ARMA; empirical mode decomposition (EMD); least squares support vector machines (LSSVM)

国家自然科学基金(51378304)

2015-07-06修改稿收到日期：2015-10-06

李春祥 男，教授，博士生导师，1964年生

TU311

A DOI:10.13465/j.cnki.jvs.2016.17.006