一种基于层次划分聚类的雷达信号分选算法

何佩佩，唐霜天，匡华星

(中国船舶重工集团第七二四研究所，江苏 南京　211106)



一种基于层次划分聚类的雷达信号分选算法

何佩佩，唐霜天，匡华星

(中国船舶重工集团第七二四研究所，江苏 南京211106)

近年来，聚类分析在雷达信号分选领域中得到了大量的关注。大部分算法聚类数需要事先人为设定，为了解决这一问题，将基于层次划分的聚类算法应用到雷达信号分选当中。该算法通过数据各个维度的差与对应阈值的比较进行分类，并提出一种基于“点对”的平均距离的评价指标来确定最佳聚类，无需人为设定聚类数，可实现自动聚类。仿真实验表明，此算法对参数固定和参数变化的雷达都具有良好的分选能力，分选准确率较高。

雷达信号分选；聚类数；层次划分聚类；维度差；评价指标；自动聚类

0　引言

随着科技的飞速发展，现代战争中电子战变得越来越重要，而雷达信号分选是电子战中雷达侦察设备必不可少的一个功能，只有在正确分选基础上，才能对雷达信号进行参数估计和提取[1]。由于各个国家对电子战日益重视，雷达体制越来越先进，如频率捷变、重频参差、重频抖动、脉内调制等，辐射源的复杂度在日益增加，电子战所面临的电磁环境变得复杂多变，同时也让雷达信号的分选也变得更加困难[2]。

绝大多数传统的雷达信号分选算法都只是利用雷达脉冲到达时间(time of arrival，TOA)这一个参数，对其逐个进行统计直方图分析[3-5]。由于传统的利用PRI(pulse repetition interval)单参数分选的方法存在速度慢、对不完整数据和被污染的脉冲参数分选效果差、无法处理大量复杂数据等问题，已经不能适应当前复杂的信号环境[6]。为了充分利用测量脉冲的到达角(direction of arrival，DOA)、载频(radio frequency，RF)、脉宽(pulse width，PW)等参数，近年来，越来越多的聚类算法被应用到雷达信号分选中，比如k均值[7-9]、蚁群聚类[10-11]、网格聚类[12-14]等。但是其中大多数算法中的聚类数都是事先人为设定好的。针对这一问题，本文将文献[15]提出的基于层次划分的聚类算法应用到雷达信号分选中，充分应用DOA，RF，PW等参数，无需人为设定聚类数，可以实现自动聚类，并将算法针对雷达信号的特点作了一些调整，使其更适应雷达信号分选。

1　层次划分聚类分选算法

1.1算法的基本原理和步骤

基于层次划分的聚类算法是通过判断2个数据点在各个维度的差是否小于给定的阈值来确定2个数据点是否属于同一类。初始阈值为0，每个数据点单独为一类，每一次分类完成时给阈值一定的增量，再次完成分类，通过计算此过程中每一次分类的评价指标，画出曲线图，找到最佳分类情况，达到自动分类的目的[12]。

算法的流程图如图1所示。

1.2脉冲描述字的参数选择

脉冲描述字(pulse discreption word，PDW)包括到达时间(TOA)、到达角(DOA)、载频(RF)、脉宽(PW)和脉冲幅度(pulse amplitude，PA)等参数，由于脉冲幅度是一个不确定的参数，因此在没有任何先验知识的情况下选择DOA，RF，PW 3个参数进行聚类分选。如果有先验知识，针对频率捷变雷达则可以去掉RF，选择相对稳定的参数。

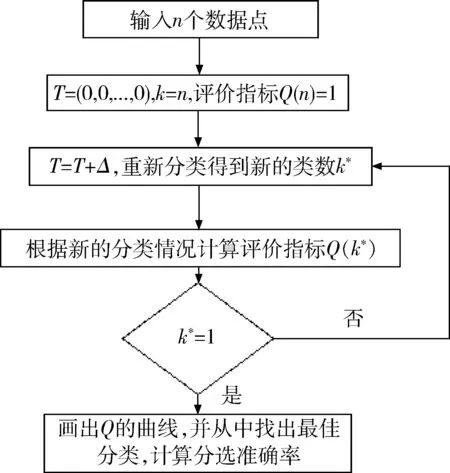
图1　算法流程图Fig.1　Algorithm flowchart

1.3阈值增量的确定

从上面的算法步骤可以看出，输入数据后首先需要确定的是每一次阈值的增量Δ。Δ并不是人为规定的，而是根据输入的数据点的分布情况来确定的，只与数据本身有关。

首先计算将数据点的每一维属性归一化，并求出每一维的中心：

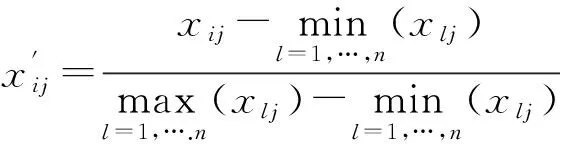
(1)

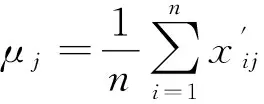
(2)

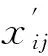
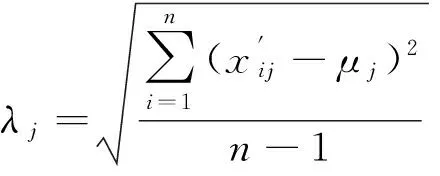
(3)

实际上λj是数据集第j维规范化的标准偏差。在高维数据的投影聚类中，正是以标准偏差为基础度量维度与类之间的相关程度。λj值越大，表明第j维属性值分布得越稀疏，与其相关的类也可能就越多。因此，利用这些维度上属性值的变化来揭示数据集潜在的类结构，并由此得出每一维对应的阈值增量：

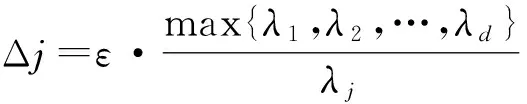
(4)

式(4)中的ε是用于控制评价指标序列精度的一个参数，ε越小，分类次数越多，结果越趋近于最优结果，但同时ε越小，算法时间开销越大，因而需要选择一个平衡点。经过多组PDW数据的反复验证，ε取0.05或0.1效果较好。

1.4评价指标

当每一次阈值增加一个增量Δ时，分类情况都有可能发生变化，此时，用评价指标Q可以评估新的分类质量，并通过比较每一次分类的评价指标得到最佳分类。与传统算法不一样的地方在于Q主要考虑数据集的几何结构。Q可由式(5)～(7)计算得出：

(5)

Sep(k)=

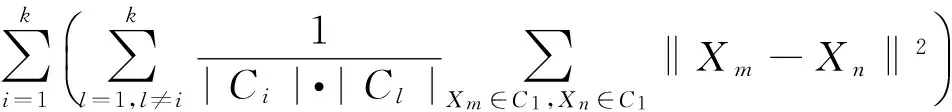
(6)

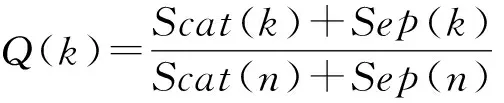
(7)

式中：Xi代表第i个数据点；Ci代表第i类；|Ci|代表第i类内的数据点个数；‖Xm-Xn‖2代表两个点的欧式距离。Scat是每类类内任意两个数据点之间距离的平方和，即类内紧凑度；Sep是将类看作是一个大“数据点”，大“数据点”间的“距离”通过类间各点的平均距离来衡量，即类间分离度。这样，Scat和Sep保持了度量上的一致性。另一方面，Scat和Sep基于“点对”的平均距离定义，可用于评价非凸形类结构的聚类质量。传统的基于几何结构的聚类有效性指标(如Vxie)通常使用类的平均半径和质心之间的距离来定义类内紧凑度和类间分离度，这样的指标往往只对球(超球)形的类结构有效。

最终得到的Q的曲线如图2所示(Q为最小值时的分类为最佳分类)。

图2　评价指标Q的曲线图Fig.2　Curve of evaluation index Q

1.5分选准确率的计算

将得到的最佳分类中的某一类与实际雷达信号一一比对，将准确分选出的信号总数除以总的信号数即为分选准确率,即

(8)

2　仿真实验

为了验证基于层次划分的聚类算法在雷达信号分选中的可行性，通过Matlab仿真生成不同体制不同参数的多部雷达来完成测试。

(1) 参数固定雷达分选测试

选用3部常规体制雷达，参数如表1所示(每个参数都加入了随机抖动)。

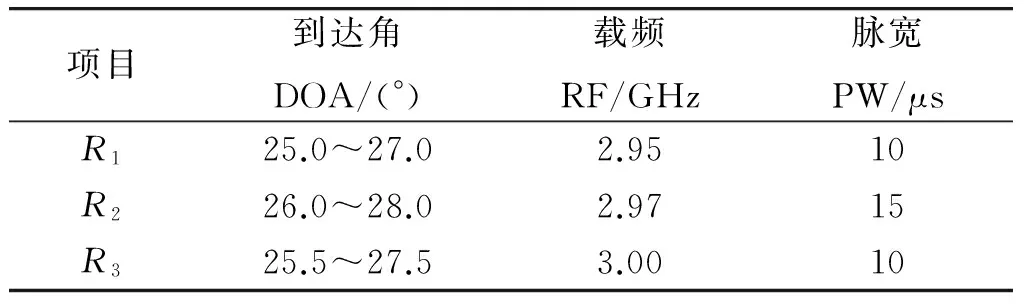
表1　雷达参数

从表1可以看到，3部雷达的DOA有不同程度的重合，并且雷达1和雷达3的PW完全一样。通过仿真生成1 s内3部雷达的PDW，并在此基础上增加了10%的虚假脉冲(干扰点)，DOA-PW分布图如图3所示(图中“.”代表雷达1，“0”代表雷达2，“△”代表雷达3，“*”代表干扰点)。

图3　DOA-PW分布图Fig.3　DOA-PW distribution

从图3中可以看出，雷达1和雷达3部分重叠在一起，并且和雷达2的DOA也有重叠。

通过本文研究的算法进行了多次分选仿真，可得出表2的数据，从表2中可以看出，总的分选准确率均在90%以上。

表2　分选准确率

(2) 参数变化雷达分选测试

选用3部复杂体制雷达，参数如表3所示。

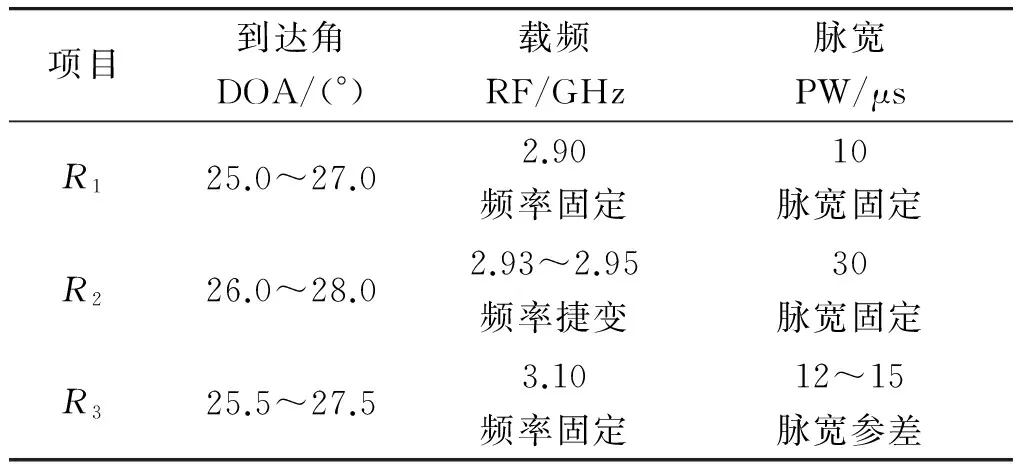
表3　雷达参数

从表3中可以看出，3部雷达的DOA有不同程度的重合，并且雷达2频率捷变，雷达3脉宽参差，同样仿真生成1 s内3部雷达的PDW并增加10%的虚假脉冲(干扰点)，DOA-PW分布图如图4所示。

图4　 DOA-PW分布图Fig.4　DOA-PW distribution

通过本文研究的算法进行了多次分选仿真，可得出表4的数据，从表4中可以看出，总的分选准确率均在90%以上。

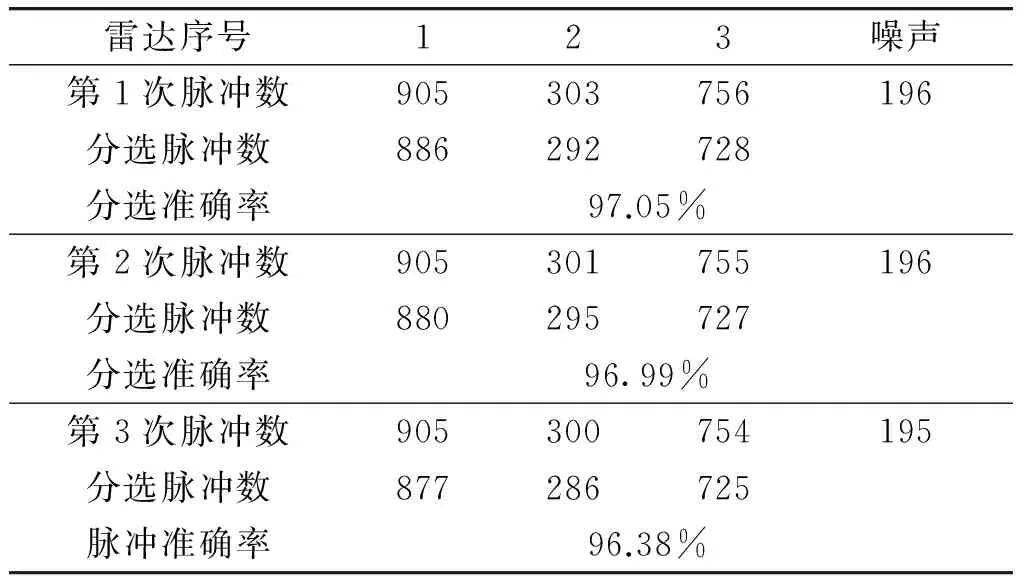
表4　分选准确率

从表1和表3可以看出，简单体制雷达和复杂体制雷达的参数并不一样，简单体制雷达设置的参数更接近，因此复杂体制雷达的分选准确率更高，但是2种情况下的分选准确率都能达到90%以上。

3　结束语

本文将基于层次划分的聚类算法用于雷达信号分选中，将算法本身的特点和信号分选的实际情况相结合，提出了一种新的思路。该算法无需任何先验信息，无需人为设定聚类数即可实现自动聚类。通过仿真实验的结果可以看出，算法对参数固定和参数变化的雷达都具有良好的分选能力，分选准确率均能达到90%以上。

[1]国强,王常虹,李峥. 支持向量聚类联合类型熵识别的雷达信号分选方法[J]. 西安交通大学学报,2010，44(8):63-67.

GUO Qiang,WANG Chang-hong,LI Zheng.Support Vector Clustering and Type-Entropy Based Radar Signal Sorting Method[J]. Journal of Xi′an Jiaotong University, 2010，44(8):63-67.

[2]倪静静,匡华星.一种新的雷达脉冲分选算法研究[J].雷达与对抗,2010,30(3):22-24.

NI Jing-jing,KUANG Hua-xing. A New Sorting Algorithm of Radar Pulses[J].Radar & ECM, 2010,30(3):22-24.

[3]易波,刘培国,薛国义. 一种基于顺序差值直方图算法的改进雷达信号分选方法[J]. 舰船电子对抗,2012，35(1):6-10.

YI Bo,LIU Pei-Guo,XUE Guo-Yi.An Improved Method for Radar Signal Sorting Based on SDIF Histogram Algorithm[J].Shipboard Electronic Countermeasure,2012，35(1):6-10.

[4]PERKINS J, COAT I. Pulse Train Deinterleaving via the Houghtransform[C]∥ IEEE International Conference on Acoustics, Speech,and Signal Processing,1994:197-200.

[5]CHAN Y T, CHAN F,HASSAN H E. Performance Evaluation of ESM Deinterleaver Using TOA Analysis. Microwaves, Radar and Wireless Communications[R].2002,MIKON-2002:341-350.

[6]王勇刚.基于模糊聚类的雷达信号分选方法[J].电子对抗,2007(2):9-12.

WANG Yong-gang.Radar Signal Sorting Method Based on Fuzzy Clustering[J].Electronic Warfare, 2007(2):9-12.

[7]孙鑫,侯慧群,杨承志. 基于改进K-均值算法的未知雷达信号分选[J]. 现代电子技术,2010,33(17):91-93，96.

SUN Xin,HOU Hui-qun,YANG Cheng-zhi. Unknown Radar Signals Deinterleaving Based on Improved K-Means Algorithm[J]. Modern Electronics Technique,2010,33(17):91-93，96.

[8]张什永,张海黎,胡泽宾,等.基于聚类分析的雷达信号分选研究[J]. 航天电子对抗,2013,29(1):49-52.

ZHANG Shen-yong,ZHANG Hai-li,HU Ze-bin,et al. Research on Clustering-Based Radar Signal Sorting[J]. Aerospace Electronic Warfare,2013,29(1):49-52.

[9]张万军,樊甫华,谭营. 聚类方法在雷达信号分选中的应用[J]. 雷达科学与技术,2004，2(4):219-223.

ZHANG Wan-jun,FAN Fu-hua,TAN Ying. Application of Cluster Method to Radar Signal Sorting[J]. Radar Science and Technology,2004，2(4):219-223.

[10]赵贵喜,骆鲁秦,陈彬.基于改进的蚁群聚类雷达信号分选算法研究[J].电子信息对抗技术,2009,3(2):27-30.

ZHAO Gui-xi,LUO Lu-qin,CHEN Bin. Radar Signal Sorting Based on Ant Colony Clustering[J]. Electronic Information Warfare Technology,2009,3(2):27-30.

[11]赵贵喜,刘永波,谭世江,等. 基于改进LF算法的雷达信号分选[J]. 航天电子对抗,2011，27(4):31-34.

ZHAO Gui-xi,LIU Yong-bo,TAN Shi-jiang,et al. Radar Signal Sorting Method Based on Improved LF Algorithm[J]. Aerospace Electronic Warfare, 2011，27(4):31-34.

[12]何佃伟,杨承志,张荣,等.一种基于改进网格聚类的雷达信号分选算法[J]. 雷达与对抗,2011,31(2):43-49.

HE Dian-wei,YANG Cheng-zhi,ZHANG Rong,et al. A Radar Signal Sorting Algorithm Based on Improved Grid Clustering[J]. Radar & ECM, 2011,31(2):43-49.

[13]向娴,汤建龙.一种基于网格密度聚类的雷达信号分选[J].火控雷达技术,2010,39(4):67-72.

XIANG Xian,TANG Jian-long. A Method of Radar Signal Sorting Based on Grid Density Clustering[J]. Fire Control Radar Technology,2010,39(4):67-72.

[14]王军,张冰. 基于动态网格密度聚类的雷达信号分选算法[J]. 现代电子技术,2013,36(21):1-4.

WANG Jun,ZHANG Bing. A Radar Signal Sorting Algorithm Based on Dynamic Grid Density Clustering[J]. Modern Electronics Technique,2013,36(21):1-4.

[15]陈黎飞,姜青山,王声瑞. 基于层次划分的最佳聚类数确定方法[J]. 软件学报,2008，19(1):62-72.

CHEN Li-fei,JIANG Qing-shan,WANG Sheng-rui. A Hierarchical Method for Determining the Number of Clusters[J]. Journal of Software, 2008，19(1):62-72.

A Radar Signal Sorting Algorithm Based on Hierarchical Clustering

HE Pei-pei, TANG Shuang-tian, KUANG Hua-xing

(No.724 Research Institute of CSIC,Jiangsu Nanjing 211106,China)

In recent years, clustering analysis has got a lot of attention in the field of radar signal sorting. Most algorithms need to make sure of the clustering number beforehand. To solve the problem, the hierarchical clustering algorithm is used in radar signal sorting. The differences between the dimensions of the data are compared with the corresponding threshold in the algorithm. An evaluation index based on the average distance of the “point” is proposed to determine the optimal clustering. The algorithm can achieve automatic clustering without making sure of the clustering number beforehand. The simulation results show that the algorithm has good sorting ability and high sorting accuracy for both fixed parameters and changed parameters of radar.

radar signal sorting; clustering number; hierarchical clustering; dimension difference; evaluation index; automatic clustering

2015-07-07；

2015-10-20

何佩佩(1992-)，男，江苏盐城人。硕士生，研究方向为信号与信息处理。

通信地址：214125江苏省无锡市滨湖区山水城科教软件园B区2号楼E-mail：412221788@qq.com

10.3969/j.issn.1009-086x.2016.04.009

TN957.5

A

1009-086X(2016)-04-0051-05