锥导乘波体气动外形优化与分析
孟希慧,张庆兵
(北京电子工程总体研究所,北京 100854)
锥导乘波体气动外形优化与分析
孟希慧,张庆兵
(北京电子工程总体研究所,北京100854)
以高超声速巡航飞行器为应用背景,在Ma=6,H=30 km设计条件下,对锥导乘波体进行气动外形优化设计。首先以升阻比为优化目标,利用遗传算法对锥导乘波体进行气动力优化;然后对基于气动力优化得到的乘波体进行前缘钝化研究,详细分析了乘波体前缘的3种钝化半径对其气动力与气动热的影响。结果表明,采用遗传算法对乘波体工程估算的气动力进行优化是可靠的。对乘波体进行前缘钝化可以有效降低最大热流密度,但同时也会降低其升阻比。随着钝化半径的增大,乘波体升阻比降低较为明显,但对热流密度的影响逐渐减弱,因此将乘波体应用于高超声速巡航飞行器时应综合考虑钝化对其气动力和气动热的影响,寻找最佳平衡点。
高超声速;乘波体;优化设计;钝化;气动力;气动热
0 引言
高超声速巡航飞行器需要具备射程长、机动性强的能力,所以需要使用高升阻比的气动外形。传统气动外形会随着马赫数的提高遇到升阻比屏障[1],而乘波体是追求高升阻比、突破高超声速飞行器“升阻比屏障”的一种有效手段。
国内外针对乘波体的生成方法、乘波体的气动力优化研究较多。在生成方法研究方面,1959年英国的Nonweiler[2]提出利用楔形流场构造“∧”形乘波体,被认为是最早的乘波体,但该构型容积率较小,且存在较多不利于气动热防护的锐边缘,因此实用价值不高。1980年Rasmussen等[3]提出基于锥形流场生成的乘波体,与“Λ”形乘波体相比,锥导乘波体显著提高了容积率和升阻比,但是这种构型的发动机进口截面流动存在横向流动,会对吸气式发动机的工作造成不利影响。Takashima 和 Lewis等[4]提出乘波体设计的楔锥法以及 Sobieczky[5]提出的吻切锥理论较好地解决了这个问题。在气动力优化方法研究方面,Rasmussen[6]等采用高超声速小扰动理论对锥导乘波体进行了无黏气动力优化。1987年,Boweutt等[7]将黏性效应引入乘波体的优化过程中,开展了轴对称体绕流的乘波体黏性优化研究。而乘波体在高超声速飞行条件下气动加热相当严重,可能造成乘波体结构的破坏失效,所以针对乘波体进行气动力热方面的研究是有必要的。
本文针对Ma=6,H=30 km设计条件下的乘波体进行气动力热研究,分析了3种钝化半径对乘波体气动力热的影响,得到了随着钝化半径的增大,乘波体升阻比降低较为明显,但对热流密度的影响逐渐减弱的结论,研究结果对未来乘波体设计具有较强的工程应用价值。
1 锥导乘波体的生成与气动力优化
1.1锥导乘波体的生成
基于锥型流场理论,在设计条件下(如表1所示)生成锥导乘波体,生成原理如图1所示,具体生成过程参照文献[8]。
1.2气动力的工程估算
升阻比是衡量飞行器气动性能的一个重要性能参数,也是乘波体区别于其他构型的重要性能指标。

表1 来流条件

图1 锥导乘波体生成原理Fig.1 Sketch of cone-derived waverider configuration design
利用Matlab软件编程得到乘波体表面各面元的压力系数和摩擦力系数,从而通过数值积分来求得乘波体的升力系数、阻力系数和升阻比,具体计算过程参照文献[8-9]。
1.2.1无黏气动力计算
由于乘波体的上表面被设计为平行于来流方向的自由流面,压强系数为0,所以不提供升力,只需考虑下表面的压强系数cp即可。将下表面划分为三角微元后,根据各点气动参数便可利用式(1)求得压强系数cp,从而利用式(2)和(3)求得无黏升力系数cLP和波阻系数cDP。

(1)

(2)

(3)
式中:Ayn为各面元面积在Oxz平面上的投影;Azn为各面元面积在Oxy平面上的投影Sp为乘波体浸湿面积。
1.2.2有黏气动力计算
对于真实流动需要考虑黏性,利用米多尔-斯马特参考温度法可以确定出各面元的摩擦力系数cf,从而利用式(7)和(8)求得由摩擦力引起的升力系数cLf和阻力系数cDf。
高超声速层流到湍流的转捩问题还没有成熟的解决方法,因此本文假定乘波体的全表面均为充分发展的湍流。
米多尔-斯马特参考温度法给出平板上的湍流局部摩擦系数为

(4)
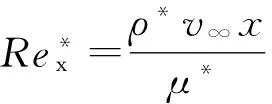
(5)


(6)

从而可求得各微元由摩擦力引起的升力系数cLf和阻力系数cDf:

(7)

(8)
式中:Avyn为各面元面积在微元y方向速度上的投影;Avzn为各面元面积在微元z方向速度上的投影。
1.3锥导乘波体的气动力优化
1.3.1优化方法
遗传算法是一种现代智能全局寻优算法,其原理是效仿生物界中的“物竞天择,适者生存”。遗传算法可以反复修改对于个体解决方案的种群,在每一步中随机地从当前种群中选择若干个体作为父代,使用它们产生子代,在连续若干代后,种群朝着优化解的方向进化。该算法不受搜索空间限制性条件(如可微、连续、单峰)的制约,不需要其他辅助性信息(如导数),这些特点使得遗传算法已成功地应用到难以用传统方法求解的复杂优化问题之中[10-11]。

P=(x2,x3,x4,x5,y1,y2,y3,y4).
(9)
未优化的乘波体前缘线在底面内(Oxy平面)的投影如图2所示。

图2 未优化的乘波体前缘线在底面内的投影Fig.2 Projection of the leading edge of non-optimized waverider
为了减少数学模型的自由度,提高优化速率,将5个点取为等间距,所以有
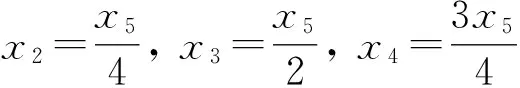
(10)
描述前缘线的数学模型简化为
P=(x5,y1,y2,y3,y4).
(11)
本文针对激波角为12°,在设计条件下,以升阻比最大作为优化目标,利用Matlab软件中的遗传算法工具箱对乘波体的外形进行优化。
1.3.2优化结果
图3给出Ma=6,H=30 km,β=12°条件下乘波体的优化收敛曲线,可以看出结果在第51代基本收敛,升阻比达到最大值5.874 61,与第1代相比提升了约14%,最大升阻比对应的最优个体值为xbest=(0.830 9,0.416 9,0.466 0,0.570 5,0.670 2),因此采用遗传算法对乘波体工程估算的升阻比进行优化是可行的。

图3 Ma=6,H=30 km,β=12°条件下乘波体的优化收敛曲线Fig.3 Optimization history at Ma=6, H=30 km,β=12°for waverider
从优化得到的前缘线出发,利用流线追踪技术得到乘波体下表面的点云坐标,将点云输入Pro/E工程软件进行曲面拟合,得到下表面,而乘波体上表面为自由来流流面,便可获得最优乘波体的三维模型, 如图4所示,其外形参数见表2。

图4 最优乘波体三维图(Ma=6,H=30 km)Fig.4 View of optimum waverider(Ma=6,H=30 km)
表2Ma=6,H=30 km,β=12°时最优乘波体的外形参数
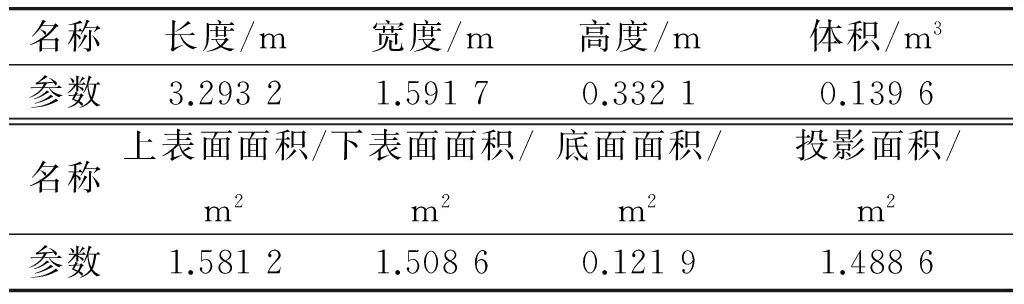
Table 2 Geometry parameters of optimum waverider at Ma=6,H=30 km, β=12°
2 优化后的乘波体气动力数值模拟
对于上述工程算法,采用数值计算方法对Ma=6,H=30 km,β=12°条件下最优乘波体的气动力性能参数进行验证,对比结果如表3所示。

表3 Ma=6,H=30 km,β=12°条件下最优乘波体气动力性能参数
由上表可以看出,数值模拟的计算结果与优化过程中采用的工程估算方法能够较好吻合,3组气动力参数的最大误差在5%之内。
3 前缘钝化对乘波体气动力热影响分析
3.1计算模型的前缘钝化
在用于计算气动力性能的乘波体模型中,其前缘是趋近于无限薄的,但在实际应用中,无论是从加工的角度还是从热防护的角度,乘波体前缘都应是进行一定钝化的。
本文采用的钝化方式为保持乘波体下表面不变,将上表面向上偏移一段距离(偏移距离为钝化直径),之后将上下表面采用圆弧过渡。采用这样的钝化方法优点在于可以尽量减少原有前缘线的位置变化,以减少其对于乘波体气动力性能的影响[12-13],钝化后的乘波体如图5所示。

图5 钝化后的乘波体Fig.5 Waverider with blunt leading edge
3.2计算格式与网格
根据文献[14-15]中的结论,Roe格式在热流计算精确性方面具有优势;与格式效应相比,网格对热流影响更大,而且驻点附近切向网格尺度对热流计算结果影响甚微,法向网格方面仅有物面第1层网格高度对热流影响巨大。本文计算中壁面附近网格高度达到1e-5 m,如图6所示。

图6 乘波体头部壁面局部网格Fig.6 Local mesh of the nose of waverider
3.3计算结果与分析
Vanmol在文献[16]中提出对于主动冷却来说,前缘半径最少需要 1 cm。利用上述钝化方法,对乘波体分别以1,1.5,2 cm 3种钝化半径值进行钝化,在设计条件下进行数值计算,得到气动力参数见表4。

表4 3种钝化半径对应的气动力参数
表4为利用CFD数值模拟得到的3种钝化半径后的气动力参数,可以看出,钝化后乘波体的阻力系数有所上升,而升力系数几乎不变,导致升阻比随钝化半径增大而变小。但对于这里所讨论的长度为3.2 m的乘波体,考虑到防热需求的前缘钝化半径并没有从本质上降低乘波体的气动力性能,仍具有较高升阻比。
钝化半径为1 cm时乘波体升阻比为4.721 8,钝化半径为1.5 cm时乘波体升阻比为4.548 2,与1 cm钝化相比降低了3.68%;当钝化半径为2 cm时乘波体升阻比为4.126 0,与1.5 cm钝化相比降低了9.28%。从图7可以看出,随着钝化半径的增大,前缘钝化对于升阻比的负面影响越来越强。

图7 升阻比随钝化半径变化趋势Fig.7 L/D at different blunt radius
对比钝化前后对称面处压力云图如图8,9所示,可以看出未钝化时,激波基本附着于前缘上;钝化半径为2 cm时,前缘激波脱体,局部形成弓形激波,导致乘波体受到的波阻增加。将未钝化和钝化半径为2 cm的波阻系数和摩阻系数结果列表,如表5所示,发现钝化后阻力系数显著增大主要是因为波阻系数显著增大,而摩擦阻力系数基本不变。

表5 钝化前后的压差阻力系数与摩擦阻力系数

图8 未钝化时对称面处压力云图Fig.8 Contours of static pressure with non-blunt leading edge

图9 钝化半径为2 cm时对称面处压力云图Fig.9 Pressure contours at symmetry plane with 2 cm blunt radius
采用Roe计算格式进行气动热计算,为了说明利用CFD数值仿真方法计算气动热的效果,本文结合半球模型进行验证。将半球模型的CFD结果与精度较高的Kemp-Riddle驻点热流计算公式[17](式(12))计算结果进行对比,如表6所示。

(12)
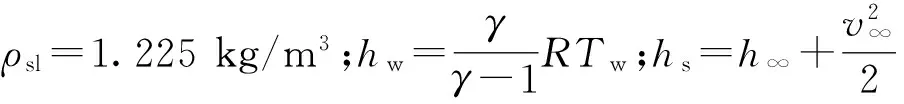

表6 半球模型3种半径对应的驻点热流
由表6可以看出,半球模型CFD的计算结果与Kemp-Riddle驻点热流计算公式的结果相差较小,3种半径对应的结果最大相差10.4%,因此可以认为利用CFD数值模拟计算热流的结果是可靠的。利用CFD数值模拟方法计算乘波体外形的驻点热流结果如表7所示,最大热流密度随半径变化趋势如图10所示。

表7 3种钝化半径对应的驻点热流
钝化半径为1 cm时乘波体最大热流密度为387.081 1 kW/m2,钝化半径为1.5 cm时乘波体最大热流密度降至335.960 4 kW/m2,与1 cm钝化相比降低了13.21%;当钝化半径增大到2 cm时,乘波体最大热流密度降至306.621 5 kW/m2,与1.5 cm钝化相比降低了8.73%。从图10可以看出,随着钝化半径的增大,前缘钝化对于最大热流密度的影响越来越小。
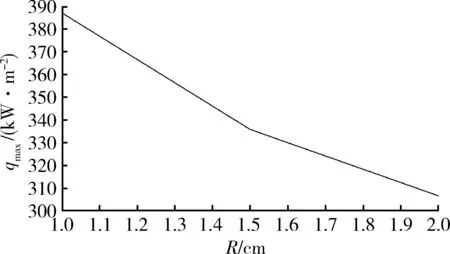
图10 最大热流密度随钝化半径变化趋势Fig.10 qmax at different blunt radiuses
4 结论
本文在Ma=6,H=30 km设计条件下,针对锥导乘波体进行气动外形优化研究,详细分析了3种前缘钝化半径对气动力热的影响,主要研究结论如下:
(1) 采用遗传算法对乘波体进行气动力优化,并将采用遗传算法优化后得到的工程估算结果与CFD数值模拟结果进行对比,发现2种方法的计算结果能够较好地吻合,表明采用遗传算法对乘波体工程估算的气动力进行优化是可靠的。
(2) 对乘波体进行前缘钝化可以有效降低最大热流密度,但同时也会降低其升阻比。
(3) 随着乘波体前缘钝化半径的增大,钝化对升阻比的影响越来越强,而对最大热流密度的影响越来越弱。因此在进行乘波体设计时,应综合考虑气动力和气动热的设计指标,选择合理的前缘钝化半径,从而达到既能有效地降低热流密度又能保证高升阻比的目的。
[1]KUCHEMANN D. The Aerodynamic Design of Aircraft[M].Oxford: Pergamon Press, 1978.
[2]NOWEILER T R F. Aerodynamic Problems of Manned Space Vehicles [J]. Journal of the Royal Aeronautical Society, 1963,67(9):521-528.
[3]RASMUSSEN M L. Waverider Configurations Derived from Inclined Circular and Elliptic Cones[J]. Journal of Spacecraft and Rocket,1980,17(6):537-545.
[4]TAKASHIMA N, LEWIS M J. Waverider Configurations Based on Nonaxisymmetric Flow Fields for Engine-AirFrame Integration[R]. AIAA-94-0380, 1994.
[5]SOBIECZKY H. Hypersonic Waverider Design from Given Shock Waves[C]∥ Proceedings of the First International Hypersonic Waverider Symposium. Maryland University of Maryland, 1990.
[6]KIM B S, RASMUSSEN M L, JISEHKE M C. Optimization of Waverider Configurations Generated from Axisymmetric Conical Flows[J]. Journal of Spacecraft and Rocket,1983,20(5):461-469.
[7]BOWCUTT K G, ANDERSON J D. Viscous Optimized Waveriders[R]. AIAA-87-0272,1987.
[8]杨海江.乘波体气动外形设计与计算[D].南京:南京航空航天大学,2008.
YANG Hai-jiang. Waverider Aerodynamic Configuration Design and Aerodynamic Performance Calculation [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008.
[9]小约翰 D 安德森.高超声速和高温气体动力学[M].杨永,李栋,译.北京:航空工业出版社,2013.
John D Anderson Jr. Hypersonic and High-Temperature Gas Dynamics[M].YANG Yong,LI Dong,Translated.Beijing: Aviation Industry Press,2013.
[10]雷英杰,张善文.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2004:1-10.
LEI Ying-jie, ZHANG Shan-wen. The Genetic Algorithm Toolbox of MATLAB and Its Application [M].Xi′an:Xidian University Press, 2004:1-10.
[11]史峰,王辉,郁磊.MATLAB智能算法30个案例分析 [M].北京:北京航空航天大学出版社, 2011:1-2.
SHI Feng, WANG Hui, YU Lei. 30 Cases of MATLAB Intelligent Algorithm[M].Beijing: Beihang University Press, 2011:1-2.[12]梅东牧,武哲,李天.乘波飞行器的优化设计和气动热计算研究[J]. 航空计算技术,2008,38(6):15-16.
MEI Dong-mu, WU Zhe, LI Tian. Research of the Waverider Optimization Design and Aerothermo Dynamics[J].Aeronautical Computing Technique, 2008,38(6):15-16.
[13]Wilson Santos. Bluntness Effects on Lift-to-Drag Ratio of Leading Edges for Hypersonic Waverider Configurations[C]∥The 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference, France, September 24-28, 2012.
[14]闫超,禹建军,李君哲.热流CFD计算中格式和网格效应若干问题研究[J].空气动力学报,2006, 24(1): 125-130.
YAN Chao, YU Jian-jun, LI Jun-zhe. Scheme Effect and Grid Dependency in CFD Computations of Heat Transfer[J]. Acta Aerodynamica Sinica, 2006, 24(1): 125-130.
[15]张建伟.高超声速再入体气动热数值模拟研究[D].济南:山东大学,2012.
ZHANG Jian-wei. Numberical Study of Aeroheating for Hypersonic Reentry Bodies[D]. Jinan:Shandong University,2012.
[16]VANMOL D. Heat Transfer Characteristics of Hypersonic Waveriders with Emphasis on the Leading Edge Effects[D].University of Maryland, College Park, 1991.
[17]姜贵庆,刘连元.高速气流传热与烧蚀热防护[M].北京:国防工业出版社,2003: 35-36.
JIANG Gui-qing, LIU Lian-yuan. Heat Transfer of Hypersonic Gas and Ablation Thermal Protection[M]. Beijing: National Defence Industry Press,2003: 35-36.
Optimization and Analysis of Cone-Derived Waverider
MENG Xi-hui, ZHANG Qing-bing
(Beijing Institute of Electronic System Engineering, Beijing 100854,China )
The optimization and analysis of cone-derived waverider is completed at the conditions ofMa=6,H=30 km. This design condition corresponds to typical hypersonic cruise conditions. The optimization of aerodynamics is completed with maximum lift over drag ratio as the first optimized objection. The CFD is used to analyze the influence of bluntness on the performance of waverider.The relations of aerodynamics and aerodynamic heating to blunt radius are obtained at three blunt radiuses. The results show that bluntness could reduce the maximum heat flux effectively, but it also reduces the aerodynamic performance. As the blunt radius increases, the aerodynamic performance reduced significantly, but its influence to the heat flux wears drops. When the aerodynamic shape of waverider is designed, the influence of bluntness to aerodynamics and aerodynamic heating should be considered synthetically and a compromise should be made between them.
hypersonic; waverider; optimized design; blunt; aerodynamics; aerodynamic heating
2015-08-18;
2015-09-20
有
孟希慧(1990-),女,天津人。硕士生,研究方向为飞行器设计。
通信地址:100854北京142信箱30分箱E-mail:15802952724@163.com
10.3969/j.issn.1009-086x.2016.04.005
TJ761.6; TJ760.1
A
1009-086X(2016)-04-0024-07

