基于迭代积分卡尔曼PHD滤波多目标跟踪

穆祥强，王朝英，危璋，孔云波

(空军工程大学 信息与导航学院，陕西 西安　710011)



基于迭代积分卡尔曼PHD滤波多目标跟踪

穆祥强，王朝英，危璋，孔云波

(空军工程大学 信息与导航学院，陕西 西安710011)

在多目标跟踪环境下，通过对数值积分卡尔曼概率假设密度滤波器(QK-PHD)的误差分析，提出一种迭代QK-PHD算法。该算法基本思想是将一步预测作为第1次迭代的初始值，通过量测更新得到状态估计，然后将此状态估计作为下一步迭代的初始均值和方差。通过多次迭代后滤波输出精度更高方差更小。Matlab仿真结果表明，在不明显增加计算时间的基础上，迭代QK-PHD比QK-PHD的跟踪效果更加明显，滤波输出精度更高。

迭代；多目标跟踪；状态估计；数值积分；卡尔曼滤波；概率假设密度滤波

0　引言

非线性滤波问题广泛存在于导航、目标跟踪、数字通信等领域，其基本任务都是从当前时刻目标状态估计和量测去估计出下一时刻的目标状态。在多目标环境下，目标的新生、衍生、合并导致目标个数动态变化，而且在观测过程中会引入大量的噪声，这些噪声影响着目标的滤波精度。Mahler[1]根据有限集[2-4]提出概率假设密度滤波器(probability hypothesis density，PHD)。该方法不需要数据关联从而得到广泛应用。

当目标的运动模型为非线性高斯情况时，为了更加精确地跟踪目标，需要采用非线性滤波。Vo等人分别提出了扩展卡尔曼PHD(extended Kalman filter PHD,EKF-PHD)和无迹卡尔曼PHD(unscented Kalman filter PHD,UKF-PHD)。但是扩展卡尔曼滤波是展开泰勒级数来线性化模型，当模型非线性化程度较大时其滤波误差比较大。迭代扩展卡尔曼滤波(iterated EKF，IEKF)[5]是基于量测信息来纠正非线性观测函数的泰勒级数展开使之重新线性化，从而减小滤波的总体误差。无迹卡尔曼[6-9](UKF)滤波受尺度参数的影响较大，使得协方差矩阵非正定，从而影响系统稳定。文献[10]提出了数值积分卡尔曼概率假设密度滤波算法，这个方法相对于扩展卡尔曼PHD和无迹卡尔曼PHD在强非线性情况下具有更好的精度和跟踪效果。文献[11]将迭代理论与容积卡尔曼相结合使得滤波算法精度更高，本文在对此文献深入的研究之后将Gauss-Newton[12]的迭代理论与QKF-PHD相结合提出了迭代数值卡尔曼概率假设密度滤波方法。在量测过程中通过迭代方法充分利用新的量测对目标状态的更新，降低了非线性的影响提高跟踪精确度。仿真结果表明，基于迭代QKF-PHD相比于QKF-PHD跟踪精度更高，更加稳定。

1　概率假设密度算法(PHD)

传统的跟踪算法如概率数据关联等算法都是通过对量测进行分配，将多目标问题转化为并行的单目标跟踪处理问题，这类算法的核心问题都是数据关联。但是当目标数过多时就会出现计算量指数增长、组合爆炸问题。概率假设密度基于有限集，利用一阶统计距近似方法对目标后验概率函数求集合积分运算，避免了直接计算完全后验概率密度[13]。因此避免了传统方法需要的数据关联步骤，因此得到广泛应用。

假设用Dk|k和Dk|k-1分别表示pk(Xk|Z1:k)和pk|k-1(Xk|Z1:k-1)的PHD其递推过程为

Dk|k-1(xk|Z1:k-1)=γk(xk)+

fk|k-1(xk|xk-1)]*Dk-1|k-1(xk-1|Z1:k-1)dxk-1，

(1)

Dk|k(xk|Z1:k)=(1-PD(xk))Dk|k-1(xk|Z1:k-1)+

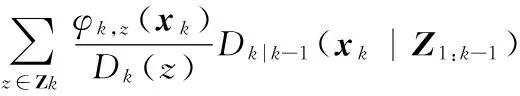
(2)

式中：D(·)表示目标强度；γk(xk)表示新生目标强度；βk|k-1(xk|xk-1)为前一时刻衍生目标强度；fk|k-1(xk|xk-1)为目标转移函数；ek|k-1(xk-1)为目标存活概率；PD(xk)为目标检测概率；φk,z(xk)=PD(xk)gk|k(z|xk)为目标似然函数;gk|k(z|xk)为单目标似然函数;Dk(z)=κk(z)+Ck(z)为量测的强度;κk(z)为杂波

Ck(z)=∫φk,z(xk)Dk|k-1(xk|Z1:k-1)dx.

2　基于迭代QKF-PHD滤波算法

2.1QKF-PHD滤波算法

非线性系统为

(3)

式中：xk∈Rm和zk∈Rm分别为状态向量和量测向量；wk-1和vk分别为系统噪声和量测噪声，服从零均值方差为Qk-1，Rk的高斯分布；f(·)和h(·)分别为状态转移函数和量测方程。

假设随机变量x，其概率密度分布服从标准的高斯分布x～N(0,1)，对于任意的关于x的函数g(x)，其积分为

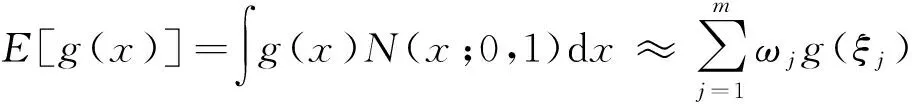
(4)

式中：ξj为积分点；ωj为权值；m为积分点个数，使用文献[14]提出了一种计算积分点的方法。构造一个三角对称矩阵J,其对角线的元素全部为0，其他元素为

(5)

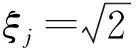
QKF-PHD的算法流程为：

设k-1时刻的后验概率假设密度的高斯形式表示为

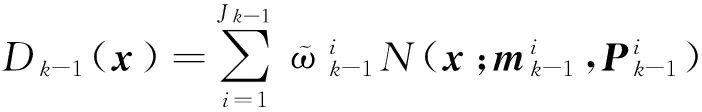
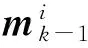
(1) 时间预测

1) 矩阵分解

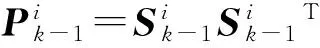
(6)

2) 求取积分点

(7)

3) 传播积分点

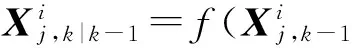
(8)

4) 状态一步预测与协方差

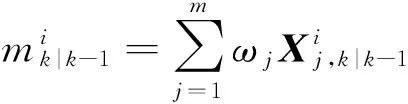
(9)

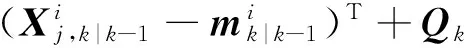
(10)

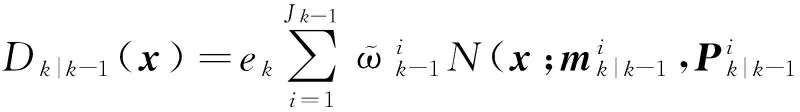
(11)

(2) 量测更新

1) 矩阵分解

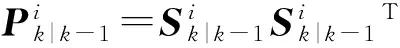
(12)

2) 求取积分点

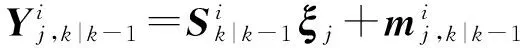
(13)

3) 传播积分点

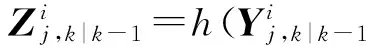
(14)

4) 量测预测以及协方差

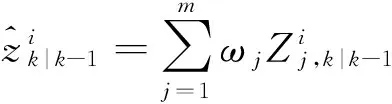
(15)

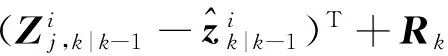
(16)

5) 互协方差

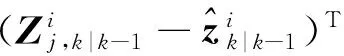
(17)

6) 滤波增益

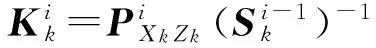
(18)

7) 计算量测更新与协方差

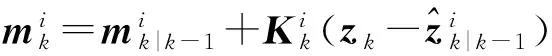
(19)

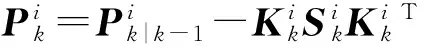
(20)

QKF-PHD的权值更新为

(21)

后验PHD为

Dk(x)=(1-Pd(x))Dk|k-1(x)+

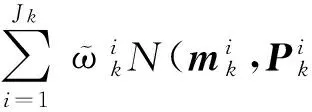
(22)

2.2迭代QKF-PHD(IQKF-PHD)算法的实现

因为在QKF的滤波算法中一步预测难免会出现误差，通过迭代不断地对量测新息与方差进行修正就可以降低误差，IQKF-PHD的时间预测方程仍如QKF-PHD，但是其量测步骤更新需改变。

IQKF-PHD算法的步骤如下：

时间更新

(23)

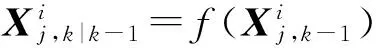
(24)

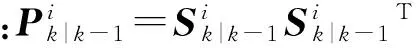
状态预测与协方差为

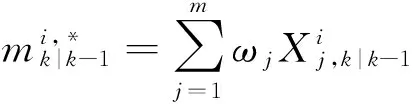
(25)

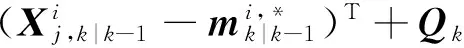
(26)

量测更新

首先计算第t次迭代的积分点与传递值为

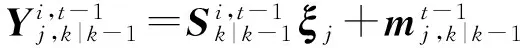
(27)

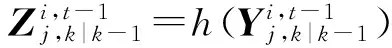
(28)

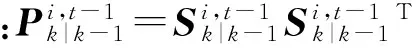
计算量测预测、新息协方差和协方差分别为

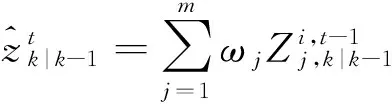
(29)

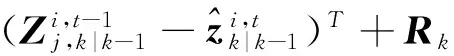
(30)

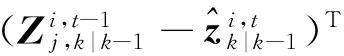
(31)

其次计算第i次迭代的滤波增益、状态估计以及协方差

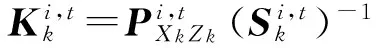
(32)

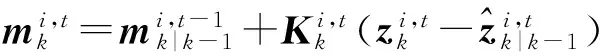
(33)

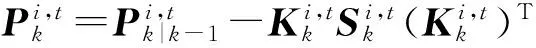
(34)

最后迭代的终止条件。终止条件为

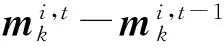
设迭代的终止的迭代次数为N，则k时刻的状态估计与方差为

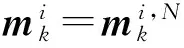
(35)

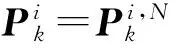
(36)

3　仿真与分析

通过试验，对比本文提出的算法与QKF-PHD，IEKF-PHD算法性能对比分析，证明本文提出算法的有效性。

(1) 试验仿真环境

设初始时刻存在2个目标，初始状态分别为(1 000,100,-1 000,-100)和(1 000,100,-3 000,100)，第3个目标出现时刻为20 s。目标做以ω=0.05 rad/s作圆周运动，目标1与目标2运动轨迹有交叉，假设目标存活概率为1，检验概率为0.95，观测站位于(0，0)。过程噪声wk-1为高斯白噪声，方差为10 m2/s2。vk为量测噪声其方差角误差为0.01 rad2，距离误差为100 m2。蒙特卡罗仿真次数为35次，选取积分点为2个。采用评价指标为最优子模型分配(optimal subpattern assignment，OSPA) 距离，在这次仿真中对势估计的惩罚程度和对状态估计的惩罚程度都取值为1。

目标跟踪模型如下

Xk=FXk-1+wk-1,

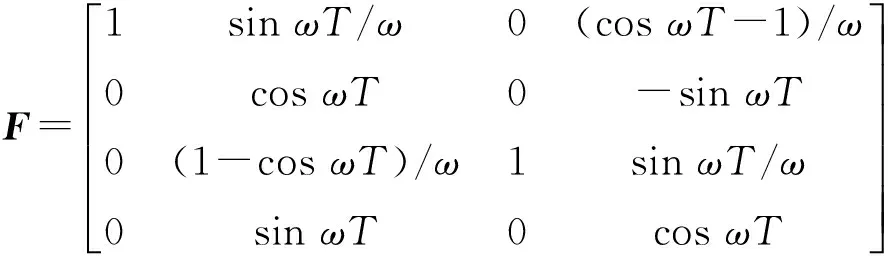
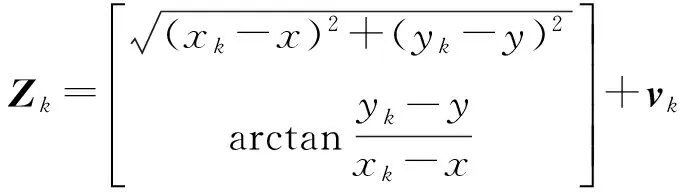
(2) 仿真结果分析

仿真结果如图1～5所示。

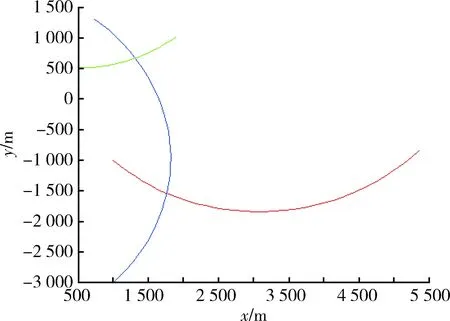
图1　目标运动轨迹Fig.1　Track of motional target

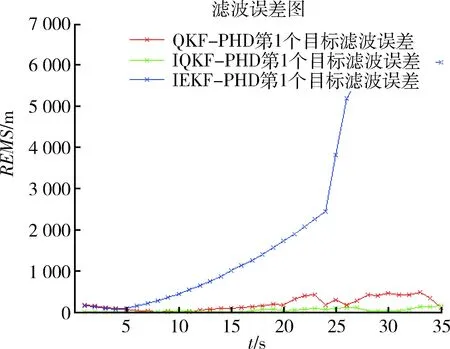
图2　第1个目标OSPA距离Fig.2　First target OSPA distance

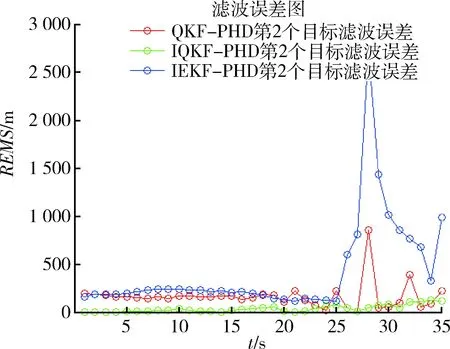
图3　第2个目标OSPA距离Fig.3　Second target OSPA distance

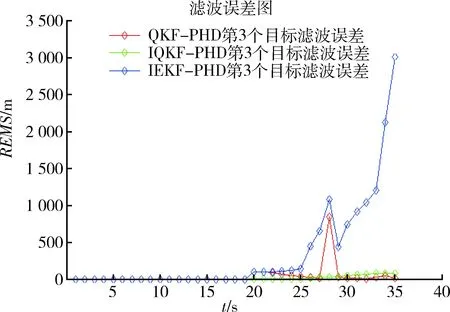
图4　第3个目标OSPA距离Fig.4　Third target OSPA distance

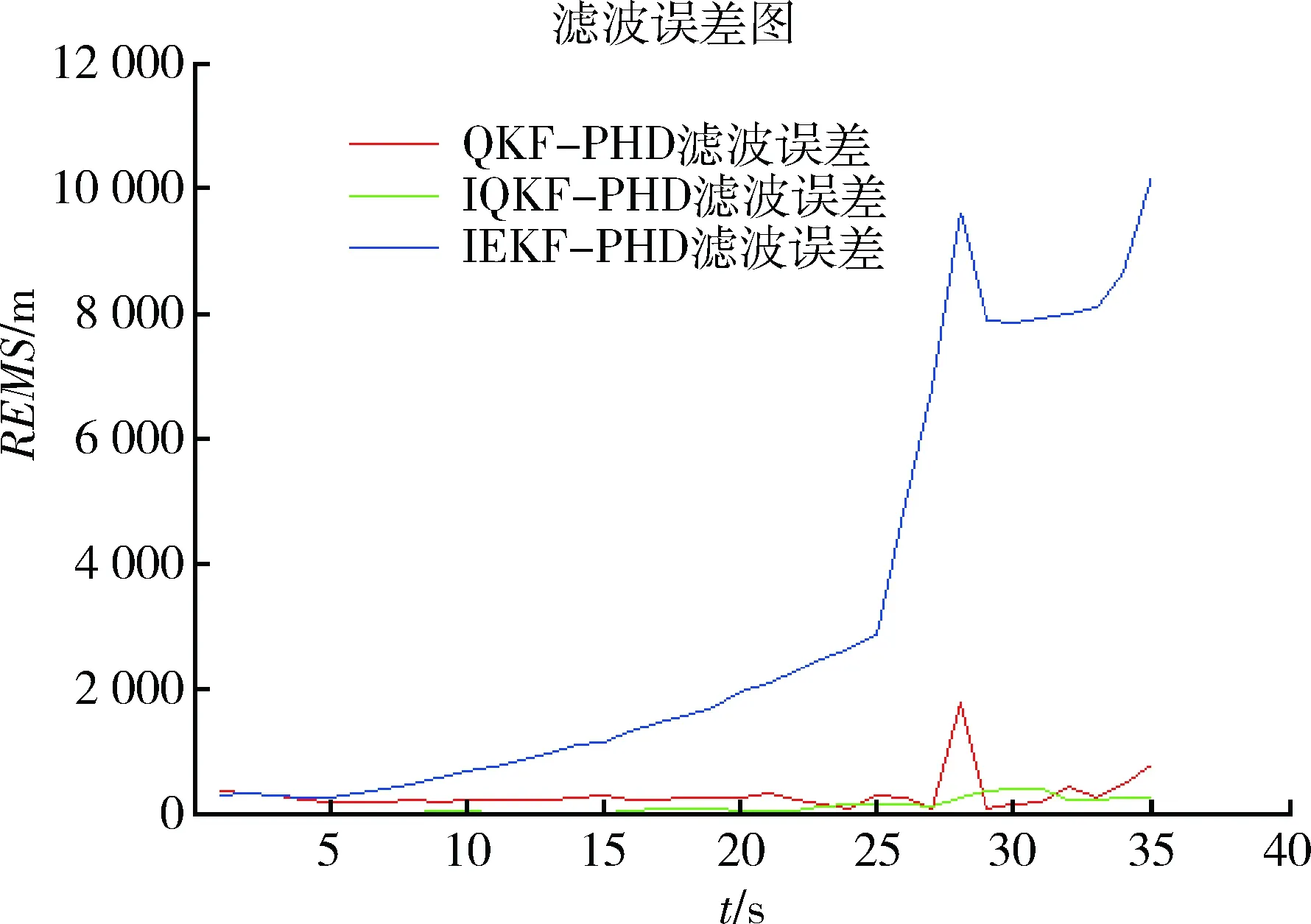
图5　目标总的OSPA距离Fig.5　Three-target OSPA distance

图1是目标的运动轨迹，其轨迹为曲线。在t=20 s时候出现第3个目标，也就是产生新的目标。从图2中可以看出IEKF-PHD算法在t=23～24 s时候还能跟踪上，但是之后算法跟踪开始发散无法跟踪目标运动。其他2种算法QKF-PHD和IQKF-PHD跟踪上了目标运动而且效果比IEKF-PHD效果要好得多。从后面2种算法的性能比较可以看出，IQKF-PHD算法的跟踪精度更高，跟踪效果最好。从图3～5中可以看出QKF-PHD与IQKF-PHD算法在跟踪目标1时后一种算法更加平稳，对每一个目标的跟踪其OSPA距离都是最低的。当t=27 s时刻目标3的运动轨迹与目标2的运动轨迹交叉，从图5可以看出其他2个算法在此时刻都出现了误差增大，而本文算法则没有。由此可得，本文提出的IQKF-PHD散发跟踪精度要明显优于其他2个跟踪算法，体现了该算法的优越性。

4　结束语

本文结合了迭代思想与QKF-PHD算法的优点提出了迭代QKF-PHD算法。该算法利用迭代思想对量测更新步骤进行迭代，充分利用了新的量测对目标状态的更新，提高了数值卡尔曼概率假设密度算法对目标跟踪精度。仿真结果表明，本文提出的算法相对与其他2种算法具有更好的跟踪效果，其稳定性与鲁棒性得到明显的提升。

[1]MAHLER R P S.Multitarget Bayes Filtering via First-Order Multitarget Moments[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1152-1178

[2]杨峰,王永齐,梁彦.基于概率假设密度滤波方法的多目标跟踪技术综述[J].自动化学报,2013,39(11):1944-1956.

YANG Feng, WANG Yong-qi, LIANG Yan.A Suivey of PHD Filter Based Multi-Target tracking[J]. Acta Automatic Sinica, 2013,39(11):1944-1956.

[3]邹其兵.多伯努利滤波器及其在检测前跟踪中的应用[D].西安：西安电子科技大学,2012.

ZOU Qi-bing. Study of Multi-Bernoulli Filter and Its Applications to Track Before Detection[D]. Xi′an:Xidian University,2012.

[4]张鹤冰.概率假设密度滤波算法及其在多目标跟踪中的应用[D].哈尔滨：哈尔滨工程大学,2012.

ZHANG He-bing.Probability Hypothesis Density Filter Algorithm and Its Application in Multi-Targets Tracking[D].Harbin:Harbin Engineering University,2012.

[5]BELL B M，CATHEY F W. The Iterated Kalman Filter Update as a Gauss-Newton Method [J]. IEEE Trans on Automatic Control, 1993, 38(2): 294-297.

[6]JULIER S J, UHLMANN J K, DURRANT-WHYTE H F.A New Method for the Nonlinear Transformation of Means and Covariance in Filters and Estimators [J]. IEEE. Transactions on Automatic Control , 2000,45(3):477-482.

[7]JULIER S J,UHLMANN J K. A New Extension of the Kalman Filter to Nonlinear System [C]∥SPIE,1997:3068,182-193.

[8]伊建君,张建秋,林青.Unsecented卡尔曼滤波-卡尔曼滤波算法[J].系统工程与电子技术，2008,30(4):617-620.

YI Jian-jun,ZHANG Jian-qiu,LIN Qing.Filter Algorithm Based on Unsented Kalman Filter [J]. Systems Engineering and Electronics,2008,30(4):617-620.

[9]JULIER S J. The Spherical Simplex Unscented Transformation[C]∥ Proc. Am. Contr. Conf. Denver, Colorado, 2003: 2430-2434.

[10]陈里铭, 陈喆, 殷福亮,等. 基于数值积分卡尔曼概率假设密度滤波的多说话人的跟踪方法[J]. 信号处理, 2012, 25(10): 1209-1214.

CHEN Li-ming, CHEN Zhe, YIN Fu-liang, et al. Quadrature Kalman PHD Filter for Multiple Speakers Tracking[J].Signal Processing,2012,25(10):1209-1214.

[11]穆静, 蔡远利. 迭代容积卡尔曼滤波算法及其应用[J]. 系统工程与电子技术，2011, 33(7): 1454-1457.

MU Jing,CAI Yuan-li. Interated Cubature Kalman Filter and Its Application[J].Systems Engineering and Electronics,2011,33(7):1454-1457.

[12]武良丹,贺西平,张小凤.超声回波参数的高斯与牛顿迭代计算[J].陕西师范大学学报,2006,34(3):56-58.

WU Liang-dan,HE Xi-ping,ZHANG Xiao-feng.The Calculation of Ultrasonic Echo Parameter by Gauss-Newton Iterative Method[J].Journal of Shaanxi Normal University,2006,34(3):56-58.

[13]王晓, 韩崇昭, 连峰. 基于随机有限集的目标跟踪方法研究及最新进展[J]. 工程数学学报, 2012, 29(4): 568-578.

WANG Xiao,HAN Chong-zhao,LIAN Feng.Survey of Target Tracking Based on Random Finite Set[J]. Chinese Journal of Engineering Mathematics, 2012,29(4):568-578.

[14]巫春玲, 韩崇昭.平方根求积分卡尔曼滤波器[J].电子学报, 2009,37(5):987-992.

WU Chun-ling,HAN Chong-zhao.Square Root Quadrature Kalman Filter[J]. Acta Electronica Sinica,2009,37(5):987-992.

[15]刘玉磊,冯新喜,鹿传国,等.带渐消因子的Quandrature卡尔曼滤波[J].宇航学报,2013,37(8):1328-1338.

LIU Yu-lei, FENG Xin-xi,LU Chuan-guo,et al.A Fading Quadrature Kalman Filter for Nonlinear Systems[J]. Journal of Astronautics,2013,37(8):1328-1338.

Probability Hypothesis Density Filter Algorithm Based on Iterated Quadrature Kalman Filter

MU Xiang-qiang，WANG Zhao-ying，WEI Zhang，KONG Yun-bo

(AFEU,Infornmation and Navigation College,Shaanxi Xi’an 710077,China)

Under the condition of multi-target tracking, by analyzing the error of quadrature Kalman probability hypothesis density filter (QK-PHD), the iterated QKF algorithm is proposed. The IQKF-PHD is used to re-estimate the one-step state and measurement predictions by virtue of the measurement updated state variable, and then the mean and variance of state variable are estimated. After several iterations, the outputs of IQKF-PHD have higher accuracy and less variance. Matlab simulation results demonstrate that the tracking accuracy and the outputs of IQKF-PHD are superior to those of QKF-PHD.

iterated;multitarget tracking;state variable; quadrature;Kalman filter; probability hypothesis density(PHD)

2015-06-19；

2015-09-21

陕西省自然科学基金(2011JM.8023)

穆祥强(1989-)，男，江苏宿迁人。硕士生，研究方向为多目标跟踪。

通信地址：201600上海市松江区九亭镇王家库路775楼2号1404室E-mail：1097516121@qq.com

10.3969/j.issn.1009-086x.2016.04.016

TN713；TP391.9

A

1009-086X(2016)-04-0095-06