浅谈风压对窗的影响
黄 锋
浅谈风压对窗的影响
黄锋
窗在风压作用下,绕定轴旋转并发生碰撞,碰撞的反力作用在窗扇的旋转轴和联接部件上;旋转轴和联接部件是窗扇受到外力作用时的主要受力部件。本文从碰撞和联接强度入手,探讨了内平开窗、外平开窗和上悬窗在风压作用下,关键受力零件强度的计算。
刚体定轴旋转;刚体碰撞;旋转轴强度;铝型材联接处强度
1.前言
现实生活中窗在风压的作用下受到损坏或掉下的现象时有发生,所以对受风压影响的窗进行力学分析非常必要。如果用流体力学理论对窗的撞击进行分析,计算过程非常麻烦,而且得出的结果多为逼近法,需经过风洞实验去验证。本文从动力学角度,根据刚体定轴旋转和刚体碰撞理论进行分析,再结合静力学理论,推导出在风的作用下旋转轴和联接受力零件的强度校核公式;并以常用产品的实际参数为例子,按佛山地区38m高度的基本风压,计算出受力零件实际承受的强度,计算结果显示:受力零件实际承受的强度小于许用强度,零件没有受到破坏,说明50年一遇的基本风压对受力零件不会产生破坏,受力零件的选材、结构设计和螺钉固定联接方式都符合日常使用要求。但现实生活中窗在风作用下有损坏和掉下现象,笔者认为原因有三个:第一受到了更高风压的作用;第二没有控制好自攻螺钉固定孔的开孔工艺尺寸;第三没有合理选择自攻螺钉的规格。
2.各种窗型开启状态下受风压的影响
2.1内平开窗开启状态下受风压的影响
2.1.1风荷载计算公式
根据《建筑结构荷载规范》(GB 50009-2012),风荷载计算公式为:

佛山地区的相关参数:
Wk—风荷载标准值(kN/m2);
µs—风荷载体型系数: 取值1.2;
µz—风压高度变化系数:取地面粗糙度类别C类,取值为1;
WO—基本风压(kN/m2):取50年一遇的基本风压为0.5kN/ m2。
佛山地区本文风荷载标准值为:

2.1.2窗扇与撑挡扇上部件碰撞的力学计算
把整窗扇当成刚体,窗扇绕合页轴定轴旋转,建立绕定轴旋转的刚体的力学模型,如图1:

图1 绕定轴旋转的刚体的力学模型示意图
S为窗扇的面积,风产生的压力为:
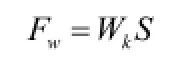
设撑挡摩擦力为40N,窗扇旋转受到的合力为:

假设窗突然受到风作用产生转动,根据刚体转动动能定理:


综合(1)(2)式得:

当窗扇旋转至90°,此时刚体与撑挡扇上部件发生碰撞,碰撞点为A;设碰撞开始和结束时,刚体的角速度分别为1ω和2ω;

又r·=ων
碰撞时,根据冲量矩定理,对旋转轴O点的冲量矩为:

由公式(1)(2)(4)(5)(6)(7)式可得:
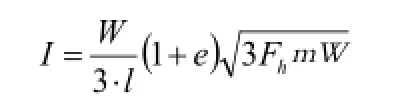
碰撞时,对于旋转O点,根据冲量定理:

由公式(4)(5)(8)(9)可得,合页轴受到的冲量为:
因e>0,由(10)式可以推断出:
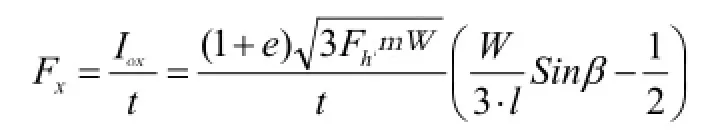
2.1.3合页轴为研究对象
2.1.3.1碰撞时合页轴的力学计算
窗只在窗重作用状态下,在yoz平面,分析合页轴受到的作用力,建立力学模型,如图2:
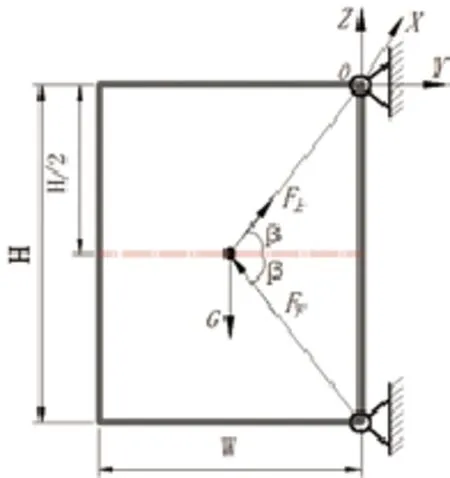
图2 合页轴受窗重作用受力模型示意图
根据力的平衡方程得:

依上述两式可得:

撞击时,单个合页轴在坐标系受到的力为:
合页扇圆环受到的力与配合的合页轴受到的力大小相等,合页扇圆环可按简支梁进行受力分析,如图3:
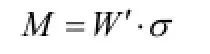
合页扇圆环到与中心轴垂直的力为xF,合页扇圆环为等截面直梁,圆环的抗弯截面模量为:
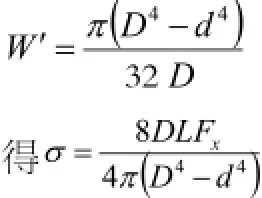
假设扇边材质为铝型材6063-T5,通过上式我们可以计算出梁的正应力,如果大于铝型材的剪切强度128MPa(抗拉强度的0.8倍),说明风作用导致的碰撞使扇边圆环失效。
2.1.3.2计算举例
按佛山地区本文风荷载标准值,假设内平开窗尺寸:W=0.75m,H=1.5m,玻璃厚度t=18mm,密度取2.6,系数为1.2,e=0.6,β=45°,l=0.17m,碰撞时间为0.01S,Dφ=15mm,dφ=10mm,L=30mm。

扇边圆环在风压引起碰撞的作用力下,实际受到的剪切强度为112.6MPa,小于铝型材6063-T5的剪切强度128MPa,扇边圆环不会受到破坏,可以承受该风压。

图3 合页扇圆环受力模型示意图
2.2外平开窗开启状态下受风压的影响
2.2.1窗与框撞击的力学计算
把整窗扇当成刚体,设窗扇绕平开滑撑作定轴旋转,建立绕定轴旋转的刚体的力学模型,如图4:

图4 绕定轴旋转的刚体的力学模型示意图
假设窗受到的合力恒定,窗处于最大开启角度上图垂直位置时开始突然受到风作用;当窗受风作用转动到上图水平位置时,与窗框四周的密封条发生撞击,根据刚体转动动能定理:
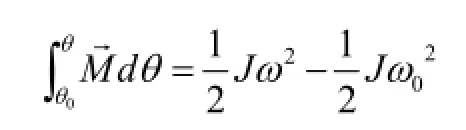

设窗扇被风作用旋转至水平位时,与窗框胶条撞击后停止,设撞击时间为t,00=t;撞击对刚体产生冲击力为'F,根据冲量矩定理:
展开得:

2.2.2旋转轴为研究对象
2.2.2.1碰撞时平开滑撑旋转轴的力学计算
以刚体为研究对象,根据力的平衡方程,对旋转轴受力分析:
窗只在窗重作用下,在yoz平面,分析旋转轴受到的作用力,建立力学模型,如图5:
根据力的平衡
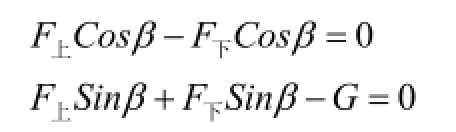
撞击时,单个外开窗滑撑的旋转轴在坐标系受到的力为:
外开窗滑撑的旋转轴为铆钉,铆钉的力学模型为悬臂梁,见图6:
对悬臂梁A点根据弯矩公式:F LM=
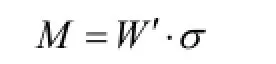
铆钉受到与中心轴垂直的力为x方向和y方向的合力

因铆钉为等截面圆直梁,圆的抗弯截面模量为:

假设铆钉材质为不锈钢,通过上式我们可以计算出梁实际承受的正应力,如果大于不锈钢的屈服强度205MPa,说明撞击使铆钉失效,最终将导致窗扇受到破坏。
2.2.2.2计算举例
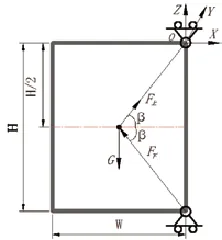
图5 旋转轴在窗重作用下的力学模型示意图

图6 铆钉的力学模型示意图
按佛山地区本文风荷载标准值,假设外平开窗尺寸:W=0.75m,H=1.2m,玻璃厚度t=18mm,密度取2.6,系数为1.2,碰撞时间为0.1S,dφ=6mm,L=3mm。

铆钉在风压引起撞击的作用力下,实际受到的正应力88MPa,小于不锈钢的屈服强度205MPa,铆钉不会受到破坏,可以承受该风压。
2.2.3碰撞时铝型材的力学计算
实际使用中,铆钉的强度一般满足要求。用于联接的滑撑、螺钉和型材,通常是应力强度最薄弱的铝型材被破坏,导致联接失效;联接通常使用自攻螺钉,下面分析撞击时窗扇铝型材联接处受剪和受拉的情况,两种情况都需校核。
2.2.3.1型材联接处受拉情况
a.窗扇铝型材受拉的力学计算
设滑撑与窗扇的安装螺钉为4个,窗扇上下一共有8个自攻螺钉,每个螺钉联接处铝型材受到的拉力为:
S为自攻螺钉对应铝板的开孔的孔壁表面积,上式求得的抗拉强度如果大于铝型材6063-T5的抗拉强度160MPa,说明撞击使螺钉联接处的铝型材受到破坏,将导致联接失效。
b.铝型材受拉计算举例
按佛山地区本文风荷载标准值,假设外平开窗尺寸:W=0.75m,H=1.2m,玻璃厚度t=18mm,密度取2.6,系数为1.2,碰撞时间为0.1S,联接铝型材板厚1.4mm,自攻螺钉孔dφ=3.5mm。
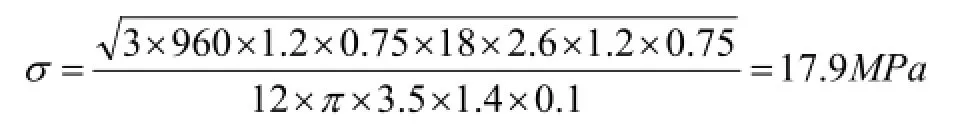
自攻螺钉联接处的铝型材在风压引起碰撞的作用力下,实际受到的拉应力为17.9MPa,小于铝型材6063-T5的抗拉强度160MPa,铝型材不会受到破坏,可以承受该风压的拉力。
2.2.3.2型材联接处受剪情况
a.窗扇铝型材受剪力的力学计算
式中: ][F — 许用联接力;
n— 一对滑撑单边(与框连接边或与扇连接边)用连接点数量,本文取4;
δ— 型材壁厚,本文取1.4;
p— 联接用螺纹的螺距,本文取1.6(ST4.8);
τ— 型材抗剪强度,一般取型材抗拉强度的0.8倍;
ξ — 多点受力不均匀系数,取1.35;
γW— 风荷载分项系数,取1.4;
α— 联接用螺纹的升角,本文取8.5°(ST4.8)。
m为窗的质量,上两式综合可得:

实际受到的拉应力,如果大于铝型材6063-T5的剪切强度说明联接处的铝型材受到破坏,将导致联接失效,最终使窗扇受到破坏或脱落。
自攻螺钉联接处的铝型材在风压引起碰撞的作用力下,实际受到的剪应力为3.87MPa,小于铝型材6063-T5的抗拉强度160MPa,铝型材不会受到破坏,可以承受该风压的剪力。
只有同时能承受风压的拉力和剪力,铝型材才不会受到破坏,否则联接失效,可能导致窗被损坏和脱落。
2.3上悬窗开启状态下受风压的影响
2.3.1窗与框撞击的力学计算
把整窗扇当成刚体,设窗绕悬窗滑撑定轴旋转,建立绕定轴旋转的刚体的力学模型,如图7:
假设窗受到的合力恒定,窗处于最大开启角度(上图虚线位置θ)时开始突然受到风作用;当窗转动到上图垂直位置时,与窗框四周的密封条发生撞击,密封条为非刚体,根据刚体转动动能定理:
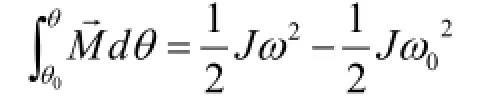
重力和F做功,根据力矩的功:

窗扇在垂直位与窗框胶条撞击后停止,根据冲量矩定理:
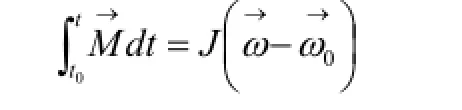
设撞击时间为t,00=t;撞击对刚体产生冲击力为'F,上式展开得:
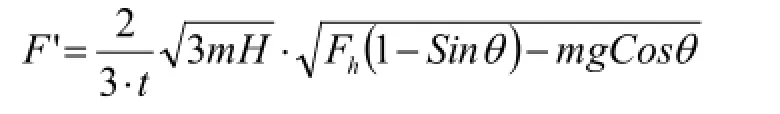
2.3.2旋转轴为研究对象
2.3.2.1碰撞时悬窗滑撑旋转轴的力学计算
以刚体为研究对象,根据力的平衡方程,撞击时,在xoy平面,悬窗滑撑每个旋转轴在x轴方向受到的作用力为:
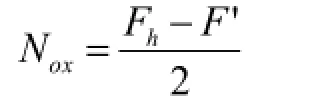
窗只在窗重作用下,在yoz平面,分析旋转轴受到的作用力,建立力学模型,如图8:
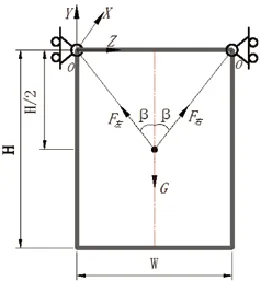
图8 窗重作用下旋转轴力学模型示意图
根据力的平衡
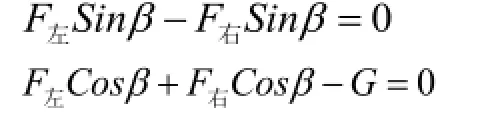
撞击时,单个悬窗滑撑的旋转轴在坐标系受到的力为:
悬窗滑撑的旋转轴为铆钉,铆钉的力学模型为悬臂梁,见图9:
对悬臂梁A点根据弯矩公式:M = FL
铆钉受到与中心轴垂直的力为x方向和y方向的合力

假设铆钉材质为不锈钢,通过上式我们可以计算出梁的正应力,如果大于不锈钢的屈服强度205MPa,说明撞击使铆钉失效,将导致窗受到破坏。
2.3.2.2计算举例
按佛山地区本文风荷载标准值,假设悬窗尺寸:W=1.2m,H=1.2m,玻璃厚度t=18mm,密度取2.6,系数为1.2,碰撞时间为0.1S,θ0=60°,dφ=6mm,L=3mm。

铆钉在风压引起撞击的作用力下,实际受到的正应力85.4MPa,小于不锈钢的屈服强度205MPa,铆钉不会受到破坏,可以承受该风压。
2.3.3碰撞时铝型材的力学计算
实际使用中,铆钉的强度一般满足要求。用于联接的滑撑、螺钉和型材中,通常是应力强度最薄弱的铝型材被破坏,导致联接失效;联接通常使用自攻螺钉,下面分析撞击时窗扇铝型材联接处受剪力和受拉力作用的情况。
2.3.3.1铝型材受拉情况
a.窗扇铝型材受拉力的力学计算
设滑撑与窗扇的安装螺钉为4个,窗扇上下一共8个自攻螺钉,每个螺钉联接处铝型材碰撞时受到的拉力为:

S为自攻螺钉对应铝板的开孔的孔壁表面积,上式求得的抗拉强度如果大于铝型材6063-T5的抗拉强度160MPa,说明撞击使螺钉联接处铝型材受到破坏,使联接失效。
b.铝型材受拉计算举例
按佛山地区本文风荷载标准值,假设悬窗尺寸:W=1.2m,H=1.2m,玻璃厚度t=18mm,密度取2.6,系数为1.2,碰撞时间为0.1S,θ0=60°,联接铝型材板厚1.4mm,自攻螺钉孔dφ=3.5mm。
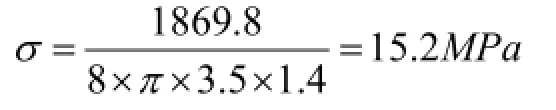
自攻螺钉联接处的铝型材在风压引起碰撞的作用力下,实际受到的拉应力为15.2MPa,小于铝型材6063-T5的抗拉强度160MPa,铝型材可以承受该风压对铝型材的拉力。
2.3.3.2铝型材受剪情况
a.窗扇铝型材受剪力的力学计算
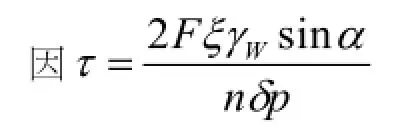
上式求得的抗拉强度如果大于铝型材6063-T5的剪切强度时,撞击使螺钉联接处铝型材受到破坏,使联接失效。
b.铝型材受剪计算举例
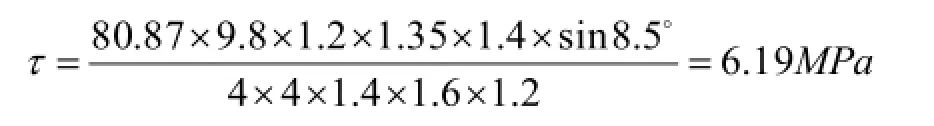
自攻螺钉联接处的铝型材在风压引起碰撞的作用力下,实际受到的剪应力为6.19MPa,小于铝型材6063-T5的抗拉强度160MPa,铝型材不会受到破坏,可以承受该风压引起对螺孔的剪力。
铝型材只有同时能承受风压的拉力和剪力,才不会受到破坏,否则联接失效,可能导致窗被破坏和脱落。
3.在实际工作中的应用
3.2本文得出三种窗型在风压作用下关键部件的强度校核公式,可根据当地风压和窗型等实际数据,计算出对应的强度值,同时与该零件材质的许用强度值进行比较,判断出门窗是否存在损坏或脱落的隐患。
3.3本文得出的关键零部件的强度校核公式,可以运用于产品研发阶段的设计计算。根据当地风压、窗型尺寸、零件的材质等条件,计算出受力零件的尺寸,确保设计的可靠性,提高研发效率。
3.4重视螺孔尺寸与螺钉长度的选用。用于联接用的自攻螺钉孔,一定要严格按照要求控制开孔的工艺尺寸。对于自攻螺钉长度的选择,以螺钉杆部刚好露出板厚为最佳,此时螺孔磨损最小,与螺钉配合最紧密。但实际工程操作中,螺孔尺寸偏大、自攻螺钉过长现象经常可见,这样大大降低了自攻螺钉的锁紧力,特别在风吹窗扇产生碰撞、震动的情况下,因型材厚度一般只有1.4mm,自攻螺钉很容易松动,这现象日积月累,窗扇脱落的可能性非常大。
4.结论
国内外报道,在风作用下,窗掉下砸人事件时有发生,给人们造成很大的损失,对社会造成不良的影响。所以当人离开家外出时,要关好窗,以免风对窗造成破坏或脱落。
[1] 《大学物理》.高等教育出版社
[2] 《理论力学》.高等教育出版社
[3] 《材料力学》.高等教育出版社
[4] 《建筑节能门窗配套件技术问答》.化工工业出版社
[5] 《论文汇编》.中国建筑金属结构协会
(作者单位:广东合和建筑五金制品有限公司)
TU228
B
1671-3362(2016)09-0050-06

