光伏逆变器对称短路电流特性及等效模型研究

张铭路，刘海涛，王新宝

（1.南京工程学院电力工程学院，江苏 南京 211167；2.南京南瑞继保电气有限公司，江苏 南京 211100）

光伏逆变器对称短路电流特性及等效模型研究

张铭路1，刘海涛1，王新宝2

（1.南京工程学院电力工程学院，江苏 南京 211167；2.南京南瑞继保电气有限公司，江苏 南京 211100）

随着光伏发电渗透率的提高，其短路电流特性已经无法忽视。详细阐述了单级式光伏逆变器的拓扑结构、数学模型及并网控制，提出了一种基于无功电流注入的低电压控制策略。在此基础上定性分析了光伏逆变器对称短路电流特性，通过电流环控制参数设计并忽略直流电压的动态过程将其简化为受控电流源。最后，基于DIgSILENT/PowerFactory建立了详细的单级式光伏发电系统电磁暂态及受控源等值模型。仿真结果表明：当并网点电压因对称三相短路故障而导致轻度跌落或重度跌落时，电压环的动态响应是可以忽略的；当发生较深跌落但尚未使逆变器过流时，逆变器输出电流的暂态特性主要受有功电流影响；控制策略切换前后逆变器输出电流相位将发生偏移。实例分析验证了简化模型的有效性，为深入研究逆变型接口电源的故障特性奠定了基础。

光伏逆变器；低电压穿越；短路电流；等值模型；电压跌落

光伏发电系统通过逆变器和电网相连，其输出电流特性取决于逆变器控制策略，为准确计算短路故障时逆变器的输出电流，可对光伏系统各环节进行详细地动态建模，但这种方法耗时费力，因此研究光伏逆变器在短路电流分析中的等效模型很有必要。

针对逆变型电源的短路特性，国内外学者已经进行了相关的研究工作。文献［1-3］基于时域仿真结果分析了含光伏发电系统的短路特性，指出光伏逆变器可在故障期间助增短路电流，但影响有限，各种故障类型下三相电流差别不大，其大小和逆变器端口电压有关。文献［4-6］均对含逆变型电源的短路电流计算方法进行了改进。文献［4］分析逆变型电源短路电流计算方法时，假定故障前后逆变器的输出功率恒定，事实上故障时的输出功率取决于逆变器的控制策略，且分析时并未考虑逆变器限流保护。文献［5］基于前推回代法计算稳态电流，通过求解系统微分方程计算暂态电流。文献［6］指出逆变器接口电源贡献的短路电流不含暂态直流分量，视为恒定电流源。文献［5-6］在故障计算时基于较多假设和简化，计算结果误差是比较大的。

实际上，随着并网容量的增大，逆变型电源应具有一定的低电压穿越能力，因此，故障期间，其控制策略往往要做出相应调整，其故障电流特性也要发生变化。文献［7］采用含低穿的基于电网电压定向的矢量控制，通过低穿控制保证并网点电压跌落时逆变器不过流，并能根据跌落深度发出一定的无功电流来支撑并网点电压，使逆变器继续运行。文献［8-11］分析逆变型电源短路电流特性时均考虑了逆变器的低电压控制策略，但文献［9-11］中逆变器的低电压控制策略皆以德国的并网要求为准，不符合我国的工程实际。

由于故障前后，计及低电压控制的逆变器控制策略将发生改变，且故障期间，逆变器限流环节是否动作不仅和电压跌落有关还和故障前电源出力有关，因此假设故障前后功率恒定或者故障后仅考虑低穿控制使得逆变器输出电流达到限值［12］显然是不合理的。本文阐述了单级式光伏逆变器的拓扑结构及数学模型，提出了基于无功电流注入的低电压动态无功控制策略，定性分析了计及低电压控制的光伏逆变器对称短路电流特性，通过合理的假设及控制参数设计将其简化为受控电流源模型，并通过DIgSILENT仿真软件分别建立了详细的单级光伏发电系统电磁暂态模型与简化受控源模型，验证了等值模型的有效性。

1　单级式光伏逆变器拓扑结构及控制策略

1.1拓扑结构及并网控制

单级式光伏逆变器的典型拓扑结构如图1所示。

图1　单级式光伏逆变器拓扑Fig.1　Topology of single-stage photovoltaic inverter

d-q坐标系下，逆变器的数学模型如下：

式中：ugd,ugq为逆变器输出电压的d，q分量；vgd, vgq为网侧电压的d，q分量；igd,igq为网侧输入逆变器电流的d，q分量；Lf,Rf分别为网侧逆变器滤波电感和电阻；ω为电网角频率；p为微分算符。

d-q坐标系下，其网侧有功和无功功率表达式如下式：

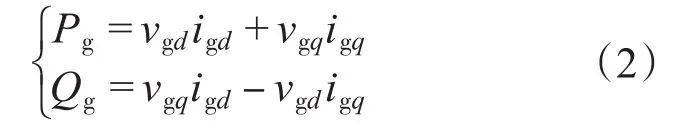
采用电网电压定向的矢量控制，将网侧电压定向在d轴上，因此有：

式中：Vg为网侧电压的有效值。

将式（3）代入式（2）可得到解耦的有功无功表达式：

正常并网时，采用定直流电压的电压外环、电流内环双闭环单位功率因数控制，即外环控制保证单级式光伏逆变器时刻处于最大功率跟踪状态，直流电压指令值Vdcref由最大功率跟踪策略得到，同时控制仅输出有功功率，将无功电流指令值igqref置零。

1.2低电压动态无功控制

对于大型光伏电站，通常要求其具有动态无功支撑能力，特别是在电力系统发生因短路故障引起的电压跌落时，光伏电站需提供无功支撑以提高低电压穿越能力。本文参考我国光伏发电站接入电力系统技术规定的国家标准［13］，采用一种基于无功电流注入的低电压动态无功控制策略，即故障期间，逆变器注入系统的无功电流igq应能跟随并网点电压变化，因此，当检测到电网发生短路故障而导致并网点电压跌落时，修正无功电流指令值igqref，使得满足下式：

式中：UT为并网点电压；IN为逆变器额定电流；均采用标幺值形式。

考虑到逆变器限流，此时，有功电流指定值igqref满足下式：

式中：imax为逆变器限流值；KP_dc,KI_dc分别为电压外环的PI增益；Vdcref,Vdc分别为直流电压指令值及实测值。

当逆变器不过流时，仍然采用定直流电压控制的并网策略给定有功电流指令值igdref，否则，闭锁电压外环，直接根据限流值关系给定。

2　逆变器电流环参数设计及简化建模

2.1逆变器电流环参数设计

基于电网电压定向矢量控制的逆变器电流内环，通过分别控制dq轴电流跟随指令值实现有功和无功的独立解耦控制。以d轴电流控制为例，其控制框图可用图2近似表示。

图2　d轴电流简化控制框图Fig.2　Simplified control block diagram of d-axis current

图2中的一阶惯性环节用来模拟电流信号采样及PWM控制的小惯性特性［14-15］，其中，Kp，Ti分别为PI控制器的比例增益和积分时间常数；KPWM为逆变器等效增益；TPWM为开关周期；Rf，Lf分别为滤波电阻和电感。d轴电流控制的近似开环传递函数为

显然，系统为典型的Ⅰ型系统，进行PI设计时，采用PI控制器的零点和阻感滤波环节的极点进行零极点对消，即令Ti=Lf/Rf，可得到标准二阶系统的闭环传递函数如下式：

根据系统参数即可计算出比例增益及积分时间常数的初值，再根据实际控制效果进行微调。同理可获得q轴电流控制的PI控制器参数。

2.2逆变器简化建模

逆变器电流内环控制的闭环传递函数，在经过前述的PI控制器参数设计后，其闭环传递函数可简化为下式：

当PWM开关频率很高时，TPWM足够小，此时，闭环传递函数的二次项系数远远小于一次项系数，因此，可忽略其二次项，最终电流环控制的闭环传递函数简化为一阶惯性环节如下式：

研究逆变器在三相对称短路故障情况下的输出短路电流特性，实际上就是分析并网点电压因故障跌落时逆变器的动态响应，而逆变器的输出主要由其控制策略决定，即便在故障情况下，输出电流特性依然可控。对应前述的单级式光伏逆变器的低电压动态无功控制策略，可知对称故障引起网侧电压跌落时，逆变器的无功电流指令值完全受并网点电压控制。而有功电流指令值根据逆变器的限流值存在2种模式：其一是未超过限流值，则继续运行于定直流电压控制的最大功率跟踪模式；其二是超过限流值，则根据限流值及无功电流指令值的关系给定。

光伏发电系统发电侧的有功输入主要与温度、光照强度等环境因素有关，而环境的变化相对缓慢，可以忽略。同时，假设直流侧大电容能维持直流电压基本恒定于满足最大功率跟踪的电压指令值，即忽略直流电压的动态调节过程，因此，考虑逆变器限值的有功电流指令值可简化为下式：

式中：P为故障前有功出力。

无功电流指令值按前述受控于并网点电压的方式给定，这样简化以后，其dq轴电流便完全受并网点电压控制，因此可将逆变器等效为一受并网点电压控制的电流源，且电流内环的动态响应用前述式（11）的一阶惯性环节模拟。由正常的并网控制策略切换至故障时的低电压动态无功控制策略后，输出三相电流的相位将发生偏移，相位差如下式：

上述的简化建模实际上是忽略了直流电压的动态调节过程，当网侧发生三相短路故障而导致并网点电压发生轻度跌落时，直流电压的波动可以忽略，或者当并网点电压发生严重跌落时，由于有功电流超过逆变器限值，电压外环迅速闭锁，这两种情况下，上述的简化建模才是合理的。若并网点电压发生较大跌落，但尚未超过逆变器限流时，直流电压波动明显，有功电流将经过一个短暂的过渡过程才能达到稳态，这种情况下，直流电压的动态调节不可忽略，上述简化建模无法模拟这种情况下的暂态过渡过程，但仍可计算其稳态下的输出电流特性。

3　实例仿真分析

为了验证前述简化建模及分析的正确性，基于德国电力系统仿真软件DIgSILENT/PowerFactory建立了详细的单级式光伏发电系统并网的电磁暂态模型及简化的压控电流源模型。其中，详细的并网模型单线图如图3所示，各母线电压等级均已在图中注明。

图3　单级式光伏发电系统并网单线图Fig.3　Single line diagram of single-stage photovoltaic system

简化建模时，将图3中虚线框内的部分用前述压控电流源代替，其余系统参数与详细建模时一致。这里采用PowerFactory自带的交流电流源并通过DIgSILENT仿真语言（DSL）编写代码使得交流电流源的输出电流受控。光伏并网系统的主要参数为：容量SN=1 MV·A，并网点电压UT= 0.38 kV，滤波电阻R=1 mΩ，滤波电感L=0.1 mH，直流稳压电容C=5 000 μF。

逆变器电流限值取其额定电流的1.5倍，考虑电流内环的动态响应，KPWM取1，fPWM取1 500 Hz，由系统参数及前述式（9）可得Kp=0.2，Ti=0.1，经实际调节，最终电流内环的PI参数为：Kp=0.4，Ti=0.1，电压外环PI参数KP_dc=0.002，KI_dc=0.05。假设系统发生三相短路故障前稳态运行时有功满发，即P=1，2 s时设置0.38 kV母线LV处发生对称三相短路故障，通过设置故障阻抗来改变并网点LV处电压的跌落深度。

1）轻度跌落。设置故障电阻为15 mΩ，故障电抗为25 mΩ，该情况下，并网点电压跌落至0.88（标幺值）左右，则其详细模型和等值模型仿真结果对比如图4所示。从上到下依次为并网点电压、单级式光伏发电系统/等值压控电流源的三相电流、电流幅值和电流幅值相对误差。

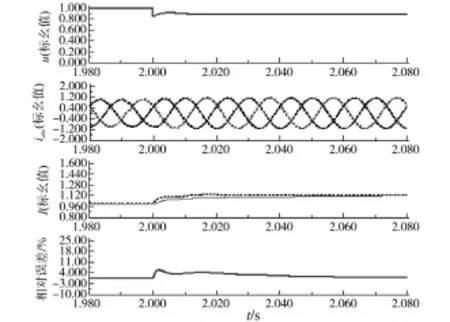
图4　轻度跌落仿真结果Fig.4　Simulation results under slight voltage sag

图4中虚线对应等值压控电流源模型的仿真结果，实线则对应详细模型。可以看出等值模型的三相电流和详细模型基本吻合，电流幅值在故障发生极短时间内稍大于详细模型，但也迅速逼近，电流幅值的最大相对误差为5.8%。这也说明，当并网点电压由于对称三相短路故障而导致轻度跌落时，电容电压基本能维持恒定，此时，可以忽略电压环的动态响应，验证了等值模型的有效性。

2）较深跌落。设置故障电阻为4.2 mΩ，故障电抗为7 mΩ，该情况下，并网点电压跌落至0.68（标幺值）左右，其详细模型和等值模型仿真结果对比如图5所示。

图5　较深跌落仿真结果Fig.5　Simulation results under deeper voltage sag

显然，当并网点电压跌落较深时，等值模型的三相电流及电流幅值均明显大于详细模型，但有逐渐吻合的趋势（2.15 s时基本吻合，限于篇幅，此处不再列出仿真结果），电流幅值最大相对误差高达24.1%。这是由于受并网点电压跌落影响，短路瞬间逆变器输出有功减小使得电源侧有功高于网侧有功，不平衡有功将引起直流电容充电导致直流电压上升，而直流电压上升将使光伏逆变器脱离最大功率跟踪状态，即直流电压高于最大功率点电压，此时电源侧发出有功将减小，而简化等值时是假设有功不变的，故简化模型输出的电流幅值在短路初期将大于详细模型，这也是误差的主要来源。经电压外环调节，一定时间后电容电压稳定于最大功率点电压，电流幅值稳定于1.49（标幺值），尚未超出逆变器电流限值。因此，这种情况下，有功电流受电压外环控制的动态特性是不能忽略的，这和前述一致。

3）重度跌落。设置故障电阻为0.6 mΩ，故障电抗为1 mΩ，该情况下，并网点电压跌落至0.28（标幺值）左右，其详细模型和等值模型仿真结果对比如图6所示。

图6中，等值模型的三相电流及电流幅值均和详细模型高度吻合，电流幅值在极短时间内便稳定于逆变器限流值，电流幅值最大相对误差为2.4%。由于并网点电压发生严重跌落，有功不平衡使得直流电容迅速充电，电压外环控制输出的有功电流指令值超过逆变器限值，电压外环迅速闭锁，此时逆变器仅由电流环控制。从并网点电压严重跌落到电压外环闭锁的时间极短，这种情况下完全可以忽略电压环的动态特性，因此等值模型的仿真结果是较为精确的，这也再次验证了等值模型的有效性。

上述3种情况下，故障前均为单位功率因数控制，三相电流与网侧电压同相位，故障后并网点电压均跌落至0.9（标幺值）以下，因此，故障后逆变器均向网侧注入无功电流，此时三相电流滞后于网侧电压，仿真计算结果分别为滞后1.0°，12.5°和42.4°，即故障后三相电流相位均发生偏移，与前述一致。

图6　重度跌落仿真结果Fig.6　Simulation results under severe voltage sag

4　结论

光伏逆变器的输出短路电流特性主要取决于逆变器的控制策略，故障情况下，控制策略往往有别于正常运行时的并网控制，需要根据故障程度做出相应调整。考虑光伏逆变器的低电压动态无功控制，通过理论分析及控制器参数设计，对详细的光伏并网电磁暂态模型进行合理简化后，等值为完全受并网点电压控制的电流源模型，仿真结果表明：

1）并网点因对称三相短路故障而发生轻度跌落时，直流电压的波动较小，可以近似保持恒定；发生重度跌落时，因逆变器的限流保护使得电压外环迅速闭锁，输出特性仅由电流环决定。两种情况下，逆变器输出电流完全受并网点电压控制，等值模型具有较高的精度。

2）并网点电压跌落较深，但尚未达到能使逆变器过流的程度时，逆变器的输出电流暂态特性主要受有功电流影响，即电压环的动态控制作用。这种情况下，输出电流幅值逐渐增大，电压环的动态响应不可忽略，等值模型仅能模拟稳态后的输出电流。

3）若对称三相短路故障使得逆变器由正常的单位功率因数并网控制过渡到注入无功电流的低电压控制时，逆变器输出的三相电流相位将由与网侧电压同相偏移至滞后于网侧电压。

［1］Afifi S N，Darwish M K，Taylor G A.Impact of Photovoltaic Penetration on Short Circuit Levels in Distribution Networks［C］//International Conference on Renewable Energy and Power Quality Conference，2014，（12）：8-10.

［2］Pandey R，Singh U，Sachdeva V，et al.Solar Photovoltaic Inverter Current Distribution During Fault on Distribution and Transmission System［J］.International Journal of Advance Research and Innovation，2014，2（1）：261-265.

［3］习伟，张哲，陈卫，等.光伏逆变器短路特性分析［J］.电力系统保护与控制，2015，43（7）：70-75.

［4］王成山，孙晓倩.含分布式电源配电网短路计算的改进方法［J］.电力系统自动化，2012，36（23）：54-58.

［5］Rajaei N，Ahmed M H，Salama M M，et al.Analysis of Fault Current Contribution from Inverter Based Distributed Generation［C］//PES General Meeting Conference&Exposition， 2014 IEEE.IEEE，2014：1-5.

［6］Cao W，Do C N，Cao J L，et al.Short-circuit Current Calculation of a Power System with a Grid-connected Inverter［C］//Advanced Materials Research，2015：823-828.

［7］王京保，曾国宏，荆龙，等.光伏并网逆变器及其低电压穿越技术［J］.低压电器，2012（17）：26-30.

［8］潘国清，曾德辉，王钢，等.含PQ控制逆变型分布式电源的配电网故障分析方法［J］.中国电机工程学报，2014，34（4）：555-561.

［9］孔祥平，张哲，尹项根，等.含逆变型分布式电源的电网故障电流特性与故障分析方法研究［J］.中国电机工程学报，2013，33（34）：65-74.

［10］吴争荣，王钢，李海锋，等.计及逆变型分布式电源控制特性的配电网故障分析方法［J］.电力系统自动化，2012，36（18）：92-96.

［11］吴争荣，王钢，李海锋，等.含分布式电源配电网的相间短路故障分析［J］.中国电机工程学报，2013，33（1）：130-136.

［12］宋国兵，常仲学，王晨清，等.直驱风机三相短路电流特性分析［J］.西安交通大学学报，2015，49（10）：1-8.

［13］GB/T 19964—2012.光伏发电站接入电力系统技术规定［S］.

［14］文珊，陈兵.分布式光伏逆变器并网侧短路暂态特性分析［J］.江苏电机工程，2014，33（6）：34-37.

［15］戴金水，吕敬.风力发电并网逆变器双闭环PI调节器的设计［J］.电工电气，2011（9）：5-9.

Research on the Characteristics of Symmetrical Short-circuit Current and Equivalent Model for the Photovoltaic Inverter

ZHANG Minglu1，LIU Haitao1，WANG Xinbao2
（1.School of Power Engineering，Nanjing Institute of Technology，Nanjing 211167，Jiangsu，China；2.NARI-Relays Electric Co.，Ltd.，Nanjing 211100，Jiangsu，China）

With the increased penetration of photovoltaic（PV）system，the short-circuit current characteristics can not be ignored.The topology，mathematical model and grid-connection method of single-stage PV inverter were described in detail.A low voltage control strategy based on the injection of reactive current was proposed.On this basis，the symmetrical short-circuit current characteristics of inverter were analyzed qualitatively，and the inverter was simplified as a controlled current source through the control parameter design of current loop and neglecting the dynamic process of the DC voltage.Finally，a detailed electromagnetic transient model and an equivalent model of single-stage PV system were established based on DIgSILENT/PowerFactory.The simulation results show that the dynamic response of the voltage loop can be neglected when the voltage of the point of interconnection sags slightly or deeply.When sag occurs and inverter current is no more than the maximum，the transient characteristics are mainly affected by the active component.The phase of inverter current will shift when control strategy is changed.Example analysis verify the validity of the equivalent model，which laid the foundation for further research.

photovoltaic inverter；low voltage ride through；short-circuit current；equivalent model；voltage sag

TM464

A

2015-08-20

修改稿日期：2016-04-10

张铭路（1990-），男，硕士研究生，Email：mingluz_njit@163.com