带有死区和摩擦补偿的机械臂伺服系统自适应神经网络控制
陈强,余梦梦,魏倩
带有死区和摩擦补偿的机械臂伺服系统自适应神经网络控制
陈强1,余梦梦1,魏倩2
(1.浙江工业大学 信息工程学院,浙江杭州 310023;2.保定市计量测试所,河北保定 071000)
针对带有输入死区和未知摩擦的机械臂伺服系统,本文提出了一种基于神经网络的自适应轨迹跟踪控制策略。首先,建立死区的逆模型,解决死区的非线性输入问题。其次,构建摩擦力动态模型,并采用径向基核神经网络来逼近系统中的不确定项。然后,通过反演法和一阶动态面,递归设计控制虚拟量和控制器,以保证系统输出能快速跟踪期望信号,提高跟踪误差的收敛性能。最后,仿真结果验证了该方法的有效性。
死区;摩擦;机械臂;自适应控制;神经网络
本文引用格式:陈强,余梦梦,魏倩.带有死区和摩擦补偿的机械臂伺服系统自适应神经网络控制[J]. 新型工业化,2016,6(8):1-8. DOI:10.19335/j.cnki.2095-6649.2016.08.001
0 引言
随着机械臂伺服系统在机器人、航空飞行器等高性能系统中的广泛应用,如何实现机械臂伺服系统的快速精确控制已经成为了一个热点问题。由于伺服系统本身具有多变量,强耦合等非线性特性,传统的PID控制器往往无法满足其高精度的控制要求[1,2]。其次,机械臂伺服系统中存在摩擦力和未知死区等非线性环节,不仅会导致控制系统的效率降低,严重时还会导致系统产生不稳定现象。因此,为提高伺服系统的控制性能,补偿死区和摩擦力等非线性环节,需要设计合适的控制方法以减弱其不良影响。
目前,针对系统中存在的死区,国内外学者已开展研究而且取得了一定的成果。其中,传统的解决死区非线性的方法一般是建立死区的逆模型或近似逆模型[3-6],并通过估计死区的上下界参数设计自适应控制器,以消除死区非线性的影响。同时,这几年在摩擦补偿控制方面有大量的研究,提出了自适应的摩擦力补偿方法[7,8],然而,这种静态模型往往并不能准确的表示摩擦力。因此,人们提出了建立动态摩擦模型[9,10],补偿摩擦对系统的影响。此外,针对系统中存在的未知函数和未知项,许多学者研究了基于神经网络[11-13]的估计方法。其中,径向基核神经网络(RBFNN),因其有效性,被广泛地应用。在提高伺服系统控制性能方面,也提出了许多先进的控制方法。其中,基于李亚普诺夫的反演法,往往能够稳定地跟踪系统的期望信号。但在反演递归步骤中,往往会因出现微分项导致微分爆炸等问题。学者提出一种动态面(DSC)控制方法[14,15],可以避免这一问题。因此,结合反演法和一阶动态面,可以简化控制器的结构,并保证系统的快速跟踪。
本文针对带有死区和摩擦的机械臂伺服系统,提出了一种基于神经网络的自适应轨迹跟踪控制方法。首先,建立死区的逆模型和摩擦动态的模型,对其进行补偿,以消除死区和摩擦对系统的影响。同时,在设计的过程中,采用神经网络来逼近系统中的不确定项,简化了控制器的设计结构。其次,结合反演法和一阶滤波器,在递归步骤中设计系统的控制虚拟量来解决反演带来的复杂爆炸度问题,提高系统的控制性能。该方法不仅能准确补偿摩擦和死区等非线性环节,而且能保证系统输出对期望信号完成有效的跟踪,提高系统的鲁棒性。
1 系统模型建立
1.1机械臂模型
机械臂是机器人运动和控制的结合点,其传统控制方法是直接转矩控制,但此类控制方法往往会存在较大误差。因此,本文中基于电压输入的机械臂系统,建立系统数学模型如下:


其中,下标n代表系统参数;gn(q)=M-1(q);Tu是系统中几种的不确定项之和,被定义为和Tf的未知不确定项,同时,不确定项是有界的,边界用ρi(i=m,c,g,f )表示,即]是系统的干扰项,对所有T∈[0,∞)来说,TL也是在边界ρd:TL≤ρd内。因此,Tu可以被限制在一定的边界内。
1.2非线性死区模型
对系统中存在的非线性死区D(ô)可以表示为

其中,τ是死区的输入;D(τ)是死区的数学模型输出;mr和ml表示死区的未知斜率;br和bl代表死区的未知宽度界限。一般情况下,假设mr>0,ml>0,br≥0和bl≤0。
对死区进行逆变换处理,使死区线性化再对其补偿,可以有效地消除死区的影响。建立死区的逆模型,τ的表达式为

则τ和D(τ)之间的误差为


2 摩擦动态模型建立
摩擦力广泛存在于伺服系统中,影响系统的控制性能,因此,首先需要对未知摩擦进行补偿。系统的非线性摩擦力可以表示为

其中,z是系统摩擦力的鬃毛形变量;x1是系统的跟踪轨迹;σ0表示刚硬强度,σ1表示阻尼系数,σ2是粘性摩擦系数。
考虑系统中的鬃毛形变量,其一阶导数可以表示为

上式鬃毛形变量z是有界的,摩擦力的模型由其一阶导的表示式推导,可表示为

其中,z的弯曲程度接近一个稳态值zs,,因此,定义
3 神经网络
在机器学习及相关领域,神经网络作为一种先进的算法,能够很好的逼近系统中存在的未知参数。因此,在本中采用神经网络函数来逼近系统中存在的不确定项。假设存在理想权重,不确定函数f可以表示为

其中,*ε为神经网络理想误差值,且满足则是一个正的常数;表输入矢量;是神经网络的基本函数;φi(X)取为以下高斯函数

其中,ci代表高斯函数的核参数;σi代表高斯函数的宽度;exp(·)代表以自然常数e为底的指数函数。
4 自适应控制和稳定性证明
4.1控制输入的设计
在本节,首先采用自适应动态面控制方法设计虚拟控制量和控制输入信号,然后利用李亚普诺夫理论证明系统的稳定性。
定义跟踪轨迹误差

对(13)求导可得


设计虚拟控制量z1为

其中,k1是设计的常数。我们设计一阶滤波器,时间常数为τ1,让z1通过一阶滤波器,α1为一阶滤波器的输出,表达式为

定义滤波误差y2为可以得到


对(18)进行转换,可得到滤波误差的导数为



对s2求导为


其中,输入矢量X1为

设计虚拟控制量z2为

其中,k2是设计的控制参数。ˆ1µ被用来估计ε1。同时,设计一阶滤波器,时间常数为τ2,使z2通过一阶滤波器,α2为一阶滤波器的输出,则表达式为






因此可以得到s3的一阶导数为


其中,输入矢量X2为

则控制输入u可设计为

其中,k3是设计的控制参数。被用来估计ε2值。
将(36)代入(35)得


其中,j=1,2。
4.2稳定性证明
定义以下李亚普诺夫函数

将(19),(29)和(37)代入到(41)中,并求导可得



5 仿真结果及分析
5.1仿真参数设置
5.2仿真结果分析

图1 关节1跟踪效果示意图Fig.1 Tracking performance of link 1

图2 关节2跟踪效果示意图Fig.2 Tracking performance of link 2
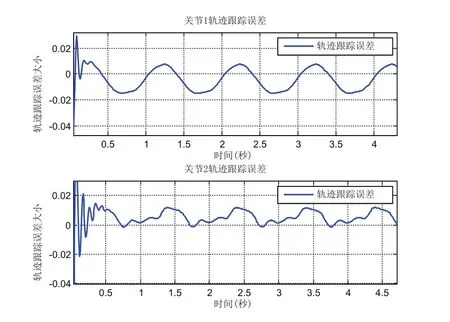
图3 系统轨迹跟踪误差示意图Fig.3 Tracking error of the system

图4 系统电压输入示意图Fig.4 Voltage input of the system
6 结论
本文针对机械臂伺服系统存在的未知摩擦和死区问题,提出一种基于神经网络的自适应控制方法。首先,分别对死区和摩擦进行建模,补偿死区和摩擦对系统的影响,有效提高系统跟踪控制性能。同时,在设计控制器的过程,本文利用神经网络来估计系统中的不确定项,简化控制器结构。然后,结合反演法和一阶动态面,避免了反演复杂度爆炸问题,保证系统误差的收敛性,并提高了系统控制性能。最后通过仿真实例,来验证该方法的有效性和优越性。上述结果表明,本文提出的方法能实现快速稳定的位置跟踪,有效补偿死区和摩擦对系统的影响,即该方法具备良好的控制性能。
[1] 解小刚,陈进.采用id=0的永磁同步电机矢量控制系统MATLAB/Simulink仿真[J].新型工业化,2016,6(5):47-54.
X G Xie,J Chen. Vector Control With id=0 Simulation of PMSM Based on Matlab/Simulink[J]. The Journal of New Industrialization,2016,6(5):47-54.
[2] 陈强,吴根忠,叶雷.永磁同步电机变负载自适应神经网络控制[J]. 新型工业化,2014,4(4):17-22.
Q Chen,G Z Wu,L Ye. Adaptive Neural Control of Permanent Magnet Synchronous Motor with Variable Load[J]. The Journal of New Industrialization,2014,4(4):17-22.
[3] J Na. Adaptive Prescribed Performance Control of Nonlinear Systems With Unknown Dead Zone[J]. International Journal of adaptive control and signal Processing,2013,27(5):426-446.
[4] J Na,X M Ren,Guido Herrmann,Q Zhi. Adaptive Neural Dynamic Surface Control for Servo Systems with Unknown Dead-zone[J]. Control Engineering Practice,2011,19(11):1328-1343.
[5] Q Chen,X Ren ,J Na,et al. Adaptive Robust Finite-Time Neural Control of Uncertain PMSM Servo System With Nonlinear Dead Zone[J]. Neural Computing & Applications,2016. DOI:10.1007/s00521-016-2260-5.
[6] G Tao,Kokotovic,et al. Adaptive Control of Plants With Unknown Hysteresis[J]. IEEE Transactions on Automatic Control,1995,40(2):200-212.
[7] J Na,Q Chen,X M Ren,et al. Adaptive Prescribed Performance Motion Control of Servo Mechanisms With Friction Compensation[J]. IEEE Transactions on Industrial Electronics,2014,61(1):486-494.
[8] Vedagarbha P,Dawson D M,Feemster M. Tracking control of mechanical systems in the presence of nonlinear dynamic friction effects[J]. IEEE Transactions on Control Systems Technology,1999,7(4):446-456.
[9] Q Chen,L Tao ,Y Nan ,et al. Adaptive Nonlinear Sliding Mode Control of Mechanical Servo System With LuGre Friction Compensation[J]. Journal of Dynamic Systems Measurement & Control,2015,138(2):021003-1-9.
[10] C I Huang,L C Fu. Adaptive Approach to Motion Controller of Linear Induction Motor with Friction Compensation[J]. IEEE/ASME Transactions on Mechatronics,2007,12(4):480-490.
[11] X M Ren,X M Rad. Identification of Nonlinear Systems With Unknown Time Delay Based on Time-Delay Neural Networks[J]. IEEE Transactions on Neural Networks,2007,18(5):1536-41.
[12] Fabri S,Kadirkamanathan V.Dynamic structure neural networks for stable adaptive control of nonlinear systems[J]. IEEE Transactions on Neural Networks,1996,7(5):1151-1167.
[13] T Zhang,S S Ge. Adaptive Neural Network Tracking Control of MIMO Nonlinear Systems With Unknown Dead Zones and Control Directions[J]. IEEE Transactions on Neural Networks,2009,20(3):483-97.
[14] W W Chen. Adaptive Backstepping Dynamic Surface Control for Systems With Periodic Disturbances Using Neural Networks[J]. IET Control Theory Appl,2009,3(10):1383-94.
[15] Q Chen,X Ren ,J A Oliver . Identifier-Based Adaptive Neural Dynamic Surface Control for Uncertain DC-DC Buck Converter System With Input Constraint[J]. Communications in Nonlinear Science & Numerical Simulation,2012,17(4):1871-1883.
Adaptive Neural Network Control of Robotic Manipulators Servo System with Friction and Dead Zone Compensation
CHEN Qiang1, YU Meng-meng1, WEI Qian2
(1College of Information Engineering, Zhejiang University of Technology, Hangzhou 310023, China; 2Baoding Institute of Measurement and Test, Baoding 071000, China)
In this paper, an adaptive control scheme based on the neural network is proposed for robotic manipulators with input dead zone and unknown friction. Firstly, the inverse model of dead zone is established to overcome the issue of input nonlinearity. Secondly, the friction behavior is described by a nonlinear dynamical model, and a radial basis function neural network (RBFNN) is employed to approximate the uncertainties in the system. Then, virtual control variables and the controller are designed by combing the backstepping technique and the dynamic surface control in each step to guarantee that the system output can rapidly track the desired signal and the convergence performance of track error can be improved. Finally, simulation results are given to verify the effectiveness of the proposed scheme.
Dead zone; Friction; Manipulator; Adaptive control; Neural network
CHEN Qiang, YU Meng-meng, WEI Qian. Adaptive Neural Network Control of Robotic Manipulators Servo System with Friction and Dead Zone Compensation[J]. The Journal of New Industrialization,2016,6(8): 1-8.
国家自然科学基金(61403343),中国博士后科学基金(2015M580521),浙江工业大学国家级大学生创新创业训练计划项目(201610337034)
陈强(1984-),男,博士,讲师,主要研究方向:非线性伺服系统建模与控制;余梦梦(1996-),女,本科生,主要研究方向:机械臂伺服系统自适应控制;魏倩(1983-),女,学士,主要研究方向:机电伺服系统计量检测与控制

