智能电网中基于自适应一致性的自动发电控制与优化
郑宇,张睿,李正佳
智能电网中基于自适应一致性的自动发电控制与优化
郑宇1,张睿1,李正佳2
(1. 南方电网科学研究院,广州 510080; 2. 苏州华天国科电力科技有限公司,苏州 215000)
针对智能电网的自动发电控制中智能体一致性问题,优化了分布式一致性协议,即提出了自适应一致性算法。设计了将分布式一致性协议中的参数不断更新的策略,并分析了自适应一致性策略的稳定性。在4区域全连通发电厂构成的智能电网中进行数值仿真,对比了无控制协议、分布式一致性协议和自适应一致性协议的控制效果,仿真结果说明了自适应一致性策略的控制效果优于分布式一致性策略,该数值仿真实验验证了所提自适应一致性协议的可行性和有效性。
智能电网;分布式控制;自适应一致性协议;负荷频率控制
0 引言
在现如今智能电网的浪潮下,分布式控制显的尤为重要。众所周知的2003年的北美大停电事件[1]也给我们提示了分布式的智能电网的重要性。而智能电网的则需有自愈和自组织能力,且需具备鲁棒性,特别是在物理因素的通讯延迟和失败的情况下[2-3]。而当大量的微电网和分布式电源接入时,分布式控制或者分层分布式控制则非常具有必要性[4-6]。为保证智能大电网的一致性,一致性控制策略则显出了重要的地位,而在通讯延迟或者失败的情况下的一致性是诸多电网一致性研究的重点[7-11]。
将电网中的每个区域看作一个智能体时,则大电网的分布式控制可看作为多智能体的分布式控制,当涉及到具体的问题时,如LFC或AGC问题时,则为多智能体的AGC一致性问题[12-13]。当电网处于稍微极端一点的情况下,网络通讯延迟或者失败造成网络拓扑结构不断发生变化,此时的一致性控制问题则为诸多学者所研究[2,14]。
一般情况下,一旦通讯拓扑检测器[2]确定了当前的通讯拓扑结构,则该控制系统的矩阵已确定。而在此时若要加快系统的收敛速度,则需要改进系统的控制策略。一致性问题的最终解决则是将系统状态变量控制到一致(一般为0),或称为收敛,其收敛的速度则由控制策略决定[15]。
而系统的控制策略在无超调的情况下,一般收敛速度较慢,而在有超调的情况下,误差减少的速度较快。若能在系统的状态变量的相对偏差较大时,采用超调较大而收敛速度较快的控制策略,待系统的状态变量的相对偏差较小时,则改为无超调而收敛速度较慢的控制策略。因此提出了一种具有自适应能力的一致性算法,并称为“自适应一致性算法”。
1 原有分布式系统的结构
原有的控制策略是集中式控制策略,其控制的结构图如图1集中式和分布式控制结构图的(a)所示。
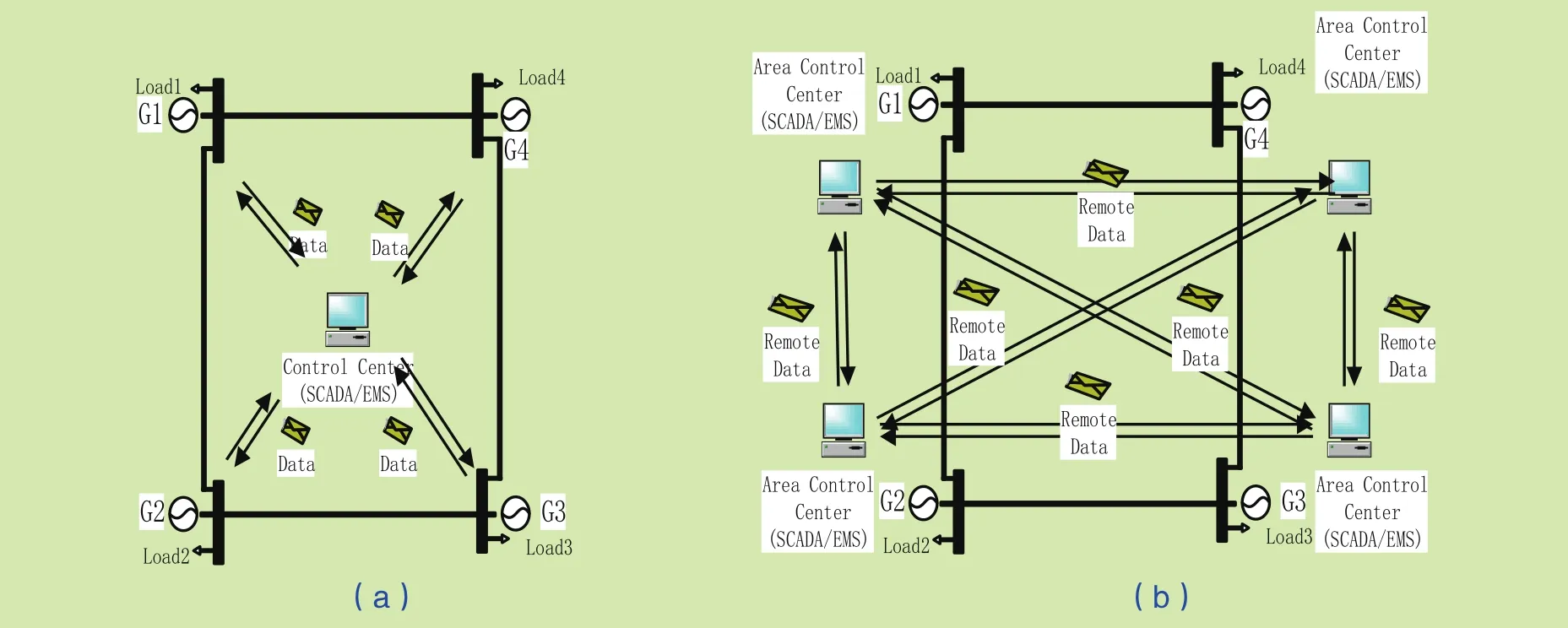
图1 集中式和分布式控制结构图Fig.1 Centralized and distributed control structure diagram
为防止随机误差且提高控制系统的鲁棒性,AGC控制需将集中式控制改为分布式控制,分布式控制结构图如图 1集中式和分布式控制结构图的(b)所示。特别是在存在分布式电源时,分布式控制策略显得尤为重要。分布式控制在子系统中则为采用局域网通讯的方式,在整个大电力系统中则采用广域网的通讯方式,其通讯的信息交流方式必须满足IEC 61850 标准。
每个区域等效为单发电机的情况,对于其区域i,其动态模型描述为


2 一致性协议设计
在实际系统中,文[2]中,每个系统的量必须和该区域本身和临近的区域相关,因此,输入变量应为

式中,Ki和Kij为常数反馈增益矩阵。将控制器纳入到大电力系统中,得到闭环的系统为
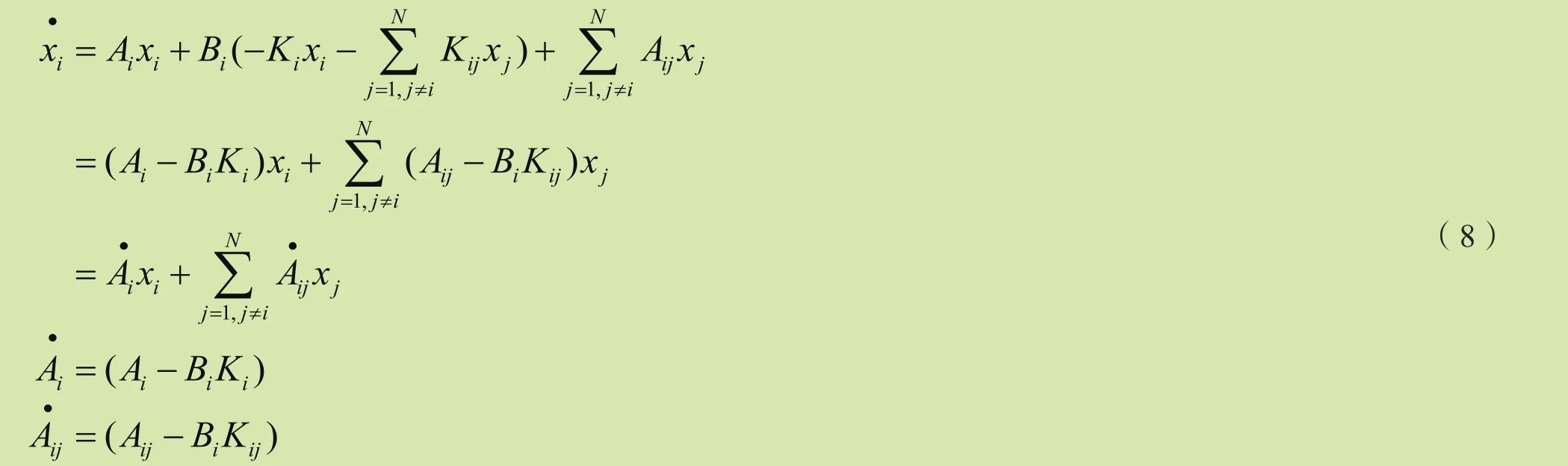
可以看出该系统的参数由Ki和Kij确定。一旦该参数确定,则系统的响应曲线都确定了。若参数选择较大则系统相应较快,然而此时的系统超调特别严重。反之当参数选择的较小时,系统不出现超调,但是其稳定的时间相应则较长。为使系统在无超调的同时达到稳定的时间小,本文设计了自适应一致性协议(或称为自适应一致性算法)。
3 一致性协议设计
从前文各式中可以看出,若不断地修正一致性协议的参数,则能达到即无超调又稳定性强的要求。因此须将此系统进行离散化处理,并在每次迭代的过程中修正一致性协议的参数。
当需处理的变量的偏差较大时,应当加大自适应一致性协议的两个参数,当需处理的变量的偏差较小时,即趋近一致时,应当减小自适应一致性协议的两个参数,因此设计一种在不断迭代过程中的自适应一致性的协议,如在第k次迭代时其不断更新的控制协议为



式中的Ka为算法自适应参数,F为非一致性协议算法的范围常数。从式子可以看出当状态变量的值小于范围常数时则令自适应算法参数为0。
4 一致性协议算法稳定性证明
文[2]中的有,将控制器纳入到大电力系统中,得到闭环的系统为

4.1引理1
当且仅当W为M矩阵时(M矩阵是L矩阵的一种,M矩阵要求它自身的逆矩阵为一个非负矩阵[14]),存在正对角矩阵D,使得DW+WTD为正定矩阵。

4.2引理2


λm,λM为通讯拓扑矩阵的最小和最大特征值。
4.3引理3
4区域中的每个区域都有局域区域控制中心,当每个区域进行通讯时,需传递的是区域的行向量信息Ri,首先假定键值(Ai,Bi)对是可控的。为寻找优化的控制器ui(t)=—Kixi(t),则在[0,tf]内代价函数最小
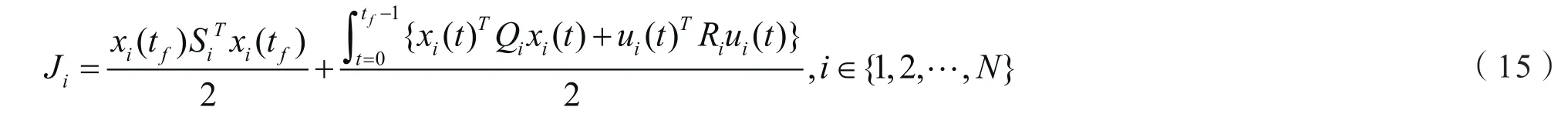
式中,Si, Qi为半正定矩阵,Ri为正定矩阵。基于有限时间范围函数的线性二次型调节器反馈控制方程为

因此解代数Riccati方程(ARE)得到正定矩阵Pi( t)

其终止条件为

为提高系统的收敛性,选择稳定状态反馈为

因Pi(∞)和Ki(∞)为在稳定状态为常数,固无需递归地证明该反馈阵的稳定性,且在不影响收敛性的情况下减少了计算负担。根据定理2,若能找到属于M矩阵的矩阵,则能推导该系统的稳定性。
存在非奇异线性变换矩阵Ti将变为,

式中Ti为

式中tik为由的第k个特征值构成的第k个右特征向量。
因此该系统的对角形式为

定义二次型李雅普诺夫函数为



5 算例与仿真
采用4个发电区域构成多智能体系统,采用所提出的自适应一致性控制协议。选择状态变量作为4区域性能指标。所有参数均由附录给出。
其单位计算功率为100MVA,采样周期为T=0.01s,每次仿真的持续时间为200s,每个异构的发电区域初始化的频率偏差0.5Hz,且假定所有的区域都处在网络全连通的情况下进行。采用MATLAB进行仿真,在相同的参数条件下,得到的无控制协议、文[2]中控制协议和自适应控制协议的对比效果,如图2ΔPtie变量的仿真效果、图3ΔPv变量的仿真效果、图 4 ΔPm变量的仿真效果、图 5 Δf变量的仿真效果和图 6所有状态变量x的仿真效果所示。
从上图可以看出,在无控制协议的情况下,系统无法稳定在同一个值,而采用文[2]中的协议,则其在相同参数的条件下稳定时间比自适应算法时间长。可以看出无控制协议时,系统无法稳定,当采用文[2]中的协议时系统的稳定时间为152.49s;当采用自适应一致性算法时系统的稳定时间为75.48s,比文[2]中的算法快50%。该仿真结果验证了自适应一致性算法的有效性和可行性。
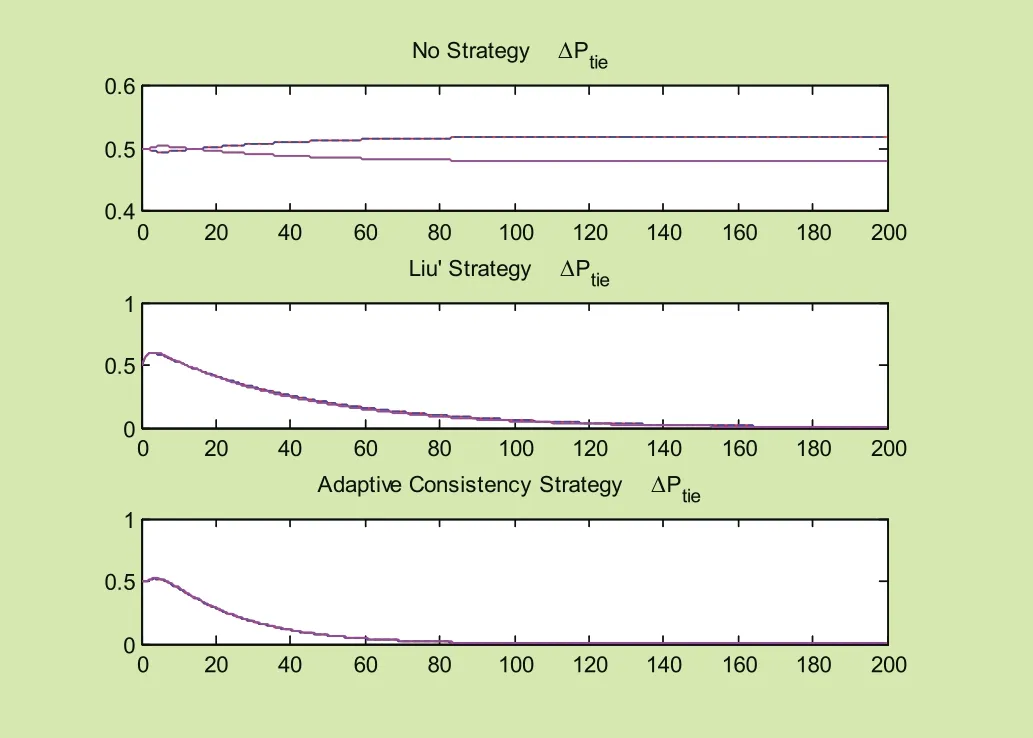
图2 ΔPtie变量的仿真效果Fig.2 Simulation results of ΔPtie
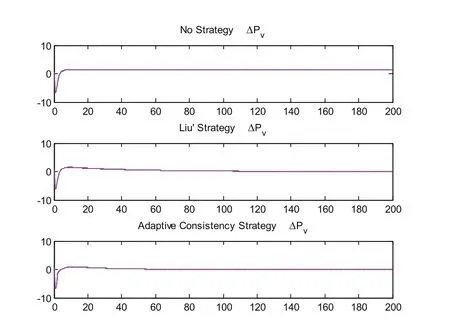
图3 ΔPv变量的仿真效果Fig.3 Simulation results of ΔPv
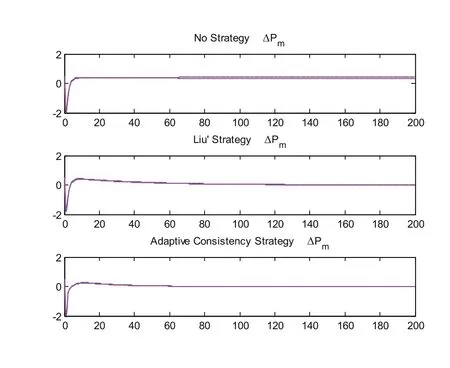
图4 ΔPm变量的仿真效果Fig.4 Simulation results of ΔPm
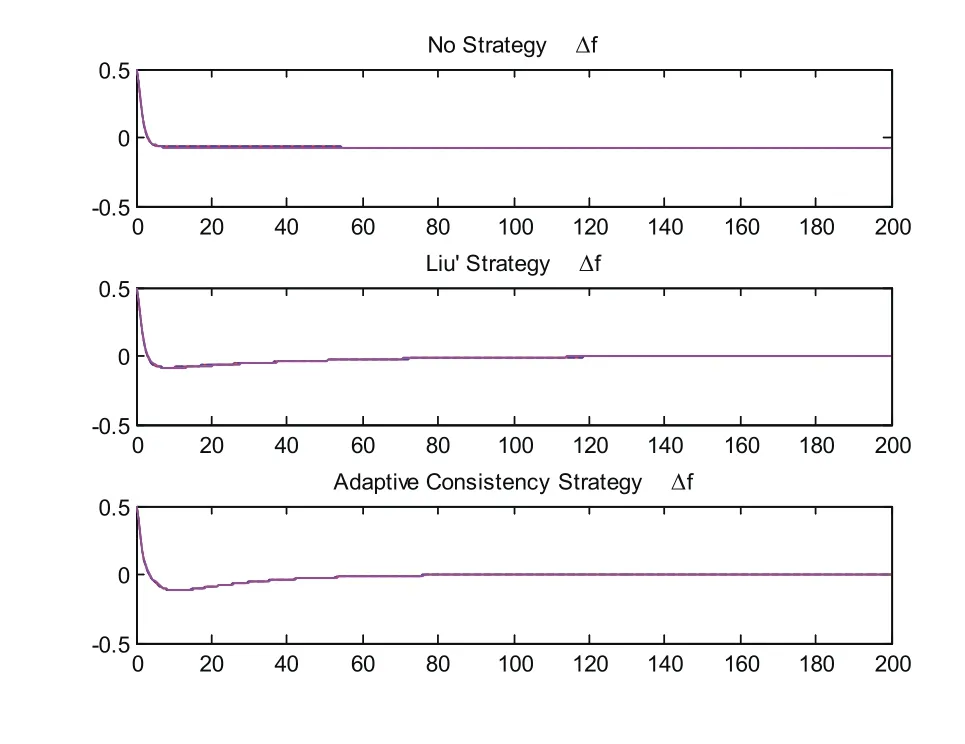
图5 Δf变量的仿真效果Fig.5 Simulation results of Δf

图6 所有状态变量x的仿真效果Fig.5 Simulation results of all state variable x
6 结论
本文在4区域全连通的通讯拓扑结构下,分析闭环系统的稳定性。提出了优化的分布式增益策略,即自适应一致性策略,并分析自适应一致性LFC协议的稳定性。针对无控制协议、分布式控制协议和自适应一致性协议三种方法,进行了对比数值仿真,数值仿真结果验证了所提自适应一致性协议优化了控制效果,减少了系统的稳定时间,所提的自适应一致性算法也被验证。
[1] Anderson G,Donalek P,et al. Causes of the 2003 major grid blackouts in North America and Europe,and recommended means to improve system dynamic performance[J]. IEEE Transactions on Power Systems 2005; 20 (4):1922 - 8.
[2] Shichao Liu,Xiaoping P. Liu,Abdulmotaleb El Saddik. Modeling and distributed gain scheduling strategy for load frequency control in smart grids with communication topology changes[J].ISA Transactions,2014,2,454-461.
[3] Healer reinforcement:A cybernetic approach to self-healing in smart grid Fereidunian,Alireza (Faculty of Electrical Engineering,K. N. Toosi University of Technology,Tehran,Iran) Source:Smart Grid Conference 2014,SGC 2014,April 20,2015.
[4] Integration of distributed generation in the power distribution network:The need for smart grid control systems,communication and equipment for a smart city - Use cases Ruiz-Romero,Salvador (Department of Control System,Electronics,and Electrical Engineering,UNED,Ciudad Universitaria,28040 Madrid,Spain); Colmenar-Santos,Antonio; Mur-Pé;rez,Francisco; Ló;pez-Rey,Á;frica Source:Renewable and Sustainable Energy Reviews,2014,38,223-234.
[5] Fault diagnosis of the smart grid with distributed generation based on limited data drive Guan,Huanxin (Shenyang Institute of Engineering,Shenyang,China); Hao,Ganggang; Zhao,Yan Source:International Journal of Grid and Distributed Computing ,2015,8(3):23-34.
[6] Electrical distribution network operation with a presence of distributed generation units in a Pre Smart Grid environment using a clusteringbased methodology Donadel,Clainer Bravin (IFES,Federal Institute of Espí;rito Santo,Av. Vitó;ria,1729,Jucutuquara,Vitoria; ES,Brazil); Fardin,Jussara Farias; Encarnaç;ã;o,Lucas Frizera Source:Energy Systems,2015,6(4):455-477.
[7] 陈鑫,余涛,席磊,等. 一种新颖的智能发电控制策略[J]. 新型工业化,2015(5):40-48.
X Chen,T YU,L Xi,et al. A Novel Policy for Smart Generation Control [J]. The Journal of New Industrialization,2015(5):40-48.
[8] 席磊,张孝顺,程乐峰,等. 基于JADE多智能体动态博弈的自动发电控制仿真平台研究[J]. 新型工业化,2014(11):5-18.
L Xi,X S Zhang,L F Cheng,et al. Research on Muti-agent simulation Platform for AGC based on JADE [J]. The Journal of New Industrialization,2014(11):5-18.
[9] K Watfa,M.,Miniaoui,S.,Al-Hassanieh,H.,& Selman,S. (2016). A Wireless Charging Infrastructure for Future Electrical Vehicular Adhoc Networks. Journal of Networks,10(9),487-500.
[10] Khalghani,M. R.,Khooban,M. H.,Mahboubi-Moghaddam,E.,Vafamand,N.,& Goodarzi,M. (2016). A self-tuning load frequency control strategy for microgrids:Human brain emotional learning. International Journal of Electrical Power & Energy Systems,75,311-319.
[11] Ropa,J.,Olak,J.,Jałmużny,W.,& Wlazło,P. Intelligent MV Switchgear as an Element of Smart Grid Network. 4/25 (2015) | 99-105
[12] Pham,T. N.,Trinh,H.,& Hien,L. V. (2016). Load Frequency Control of Power Systems With Electric Vehicles and Diverse Transmission Links Using Distributed Functional Observers. Smart Grid,IEEE Transactions on,7(1),238-252.
[13] Sambariya,D. K.,& Nath,V. Load Frequency Control Using Fuzzy Logic Based Controller for Multi-area Power System. 13(5):1-19,2016.
[14] S. Baghya Shree,N. Kamaraj,Hybrid Neuro Fuzzy approach for automatic generation control in restructured power system,International Journal of Electrical Power & Energy Systems,2016,74,274-285.
[15] Chen,Y.,Ho,D. W. C.,Lu,J.,& Lin,Z. (2016). Convergence rate for discrete-time multiagent systems with time-varying delays and general coupling coefficients. IEEE Transactions on Neural Networks & Learning Systems,27(1),178-189.
[16] K Watfa,M.,Miniaoui,S.,Al-Hassanieh,H.,& Selman,S. (2016). A Wireless Charging Infrastructure for Future Electrical Vehicular Adhoc Networks. Journal of Networks,10(9),487-500.
[17] Khalil HK.Nonlinearsystems.3rded..NewJersey:Prentice-Hall;2002.
附录
各区域的参数
Optimizing Distributed Gain Scheduling Strategy for Load Frequency Control in Smart Grids Based on Adaptive Consensus Protocol
ZHENG Yu1, ZHANG Rui1, LI Zheng-jia2
(1.Electric Power Research Institute, China Southern Power Grid Co., Ltd., Guangzhou 510080, China; 2.Suzhou Huatian Power Technology Co., Ltd., Suzhou 215000, China)
In order to solve the consensus problem of Load Frequency Control (LFC, or Automatic Generation Control,AGC) in smart grids, a distributed consensus protocol is optimized and an Adaptive Consensus Protocol (ACP) is proposed. The ACP parameters continuously updated strategy is designed, and the stability of the ACP is analyzed. Simulated with four power area all connected in smart grids, comparing with the three control protocols include none protocol, distributed consensus protocol and the ACP. The simulation results show that the ACP is better than the others. The correctness and effectiveness of the ACP is verified form the simulation result.
Smart grids; Distributed consensus control; Adaptive consensus protocol; Load frequency control
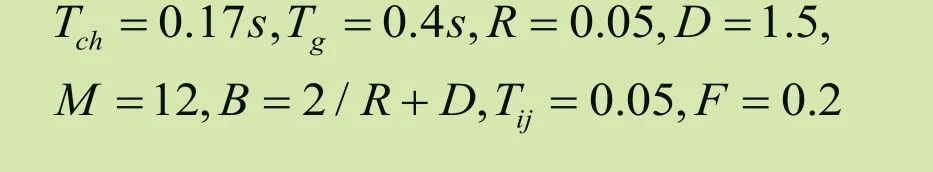
10.19335/j.cnki.2095-6649.2016.08.006
ZHENG Yu, ZHANG Rui, LI Zheng-jia. Optimizing Distributed Gain Scheduling Strategy for Load Frequency Control in Smart Grids Based on Adaptive Consensus Protocol[J]. The Journal of New Industrialization,2016,6(8): 41-48.
中国南方电网科技项目资助(WYKJ00000027).
张睿(1983-),女,工学博士,博士后。主要从事电力系统运行和控制、数据挖掘、智能电网、能源互联网等方面的研究工作;郑宇(1987-),男,工学博士,博士后。主要从事电力系统规划、智能电网、能源互联网等方面的研究工作;李正佳(1972-),男,高级工程师,硕士。主要从事电力通信、电力系统行业等研究工作
本文引用格式:郑宇,张睿,李正佳.智能电网中基于自适应一致性的自动发电控制与优化 [J]. 新型工业化,2016,6(8):41-48.

