GPS起算点对于其精度的影响
张发平
【摘 要】通过分析介绍GPS起算点精度和网形选择对于GPS解算成果精度的影响,在GPS起算点选择上提出了介于实际可操作的方案和方法,并结合起算点选择对网形的布置提出了优化方案,为保证GPS网在约束条件下解算成果的精度提供参考依据;最后结合项目实地测绘的成果对结论进行了验证。
【关键词】GPS测量;起算点;约束平差;高程拟合
随着GPS定位的技术越来越完善,GPS定位技术已经在大地测量、精密工程测量、一级变形监测与分析等诸多领域得到了广泛的应用,而利用GPS定位技术建立控制网已成为一种主要的测量技术手段,特别是在工程测量控制网领域,GPS定位技术已经几乎完全取代了常规测量方法。GPS控制网的合理布设对保证控制网的精度,提高控制网布设的效率和降低建网费用提出了更高的要求。为此文章通过在联测起算点,基于起算点的网形选择等方面进行了论述。
一、起算点验证的意义
我们都知道GPS测量的直接坐标成果属于WGS-84地心坐标系,而在工程领域我们常用的国家坐标系或者地方坐标系等属于参心坐标系统,因此需要将GPS测量成果转换为国家(或地方)的二维(或三维)坐标系统的相应成果。转换的主要方法是利用布尔莎七参数模型将地面控制点(已知点)作为约束条件,GPS网强制符合到地面控制点(已知点)所在的坐标系中,我们将这些两个网中都有的点称为重合点。由于我国的国家控制点布设时间较久,在许多地区破坏严重,加之由于当时技术条件的限制,我国西部地区的平差方法本来就较之东部缺乏严谨,使得原有控制点的坐标精度的可靠性降低。
重合点的误差和点位分布对于GPS网约束平差的精度有着至关重要的作用,若将存在粗差或者较大明显误差的已知点作为平差计算或坐标转换的约束条件,其结果必使得GPS无约束平差的观测结果可靠性降低,严重的情况可能会使GPS定位结果失去测量意义。因此,在对GPS网进行约束平差前,对GPS控制网的已知点进行粗差探析是十分必要的。故在布设GPS控制网点时,对起算数据(已知点)的可靠性探析是保证GPS精度的前提条件。
二、起算数据的验证方法
在进行GPS网的约束平差或联合平差时,为保证GPS解算结果的精度不随约束数据的影响而显著降低,对起算数据进行误差探析和验证是必要的。传统的起算数据验证方法主要有:
方差检验法:在进行约束平差时,以三维无约束平差所得到的验后的单位权方差作为先验的单位权中方差,逐个加入起算数据进行平差计算,同时检验验后的单位权方差与先验的单位权方差的相容性:当在加入某一起算数据后发现不一致,则说明起算数据可能存在质量问题。
附和线路法:采用多条附和路线,从一个起算点通过一个由GPS导线推算另一个计算点的坐标,将此坐标和已知值作比较,根据他们的差异值的大小来判断起算点的质量。
检查点法:平差计算时,不是将所有的起算点坐标固定,而是保留一个点作为检查点,平差后比较该点坐标的平差值和已知值,根据他们的大小来判断起算点质量的好坏。为了准确的判断起算点质量的好坏,一般需要轮换地将各个起算点分别作为检查点。
三、起算点精度和其分布对解算结果的影响
通过以上的论述和实际测绘工作的经验,在当前技术情况下,约束平差的精度通常比无约束平差的精度低。当起算数据有4个或4个以上时,可以利用附和线路法和检查点法对起算点进行验证,剔除误差相对大的起算点,以保证约束平差后,GPS单位权中误差符合规范要求。然而在实际工程中经常遇到的起算数据只有3个,起算数据精度本身不匹配(人为破坏、自然环境(风化、沉降等)引起的变化、技术条件限制等)、位置关系不理想的情况,我们不能简单的以数据平差处理后平差的中误差来判定起算数据精度的好坏。
GPS控制网的布设中,GPS已知点位的分布作为GPS解算的约束条件,对于GPS的解算成果有至关重要的作用。我们得知,某个未知点位距离已知点越远,其可靠性越低,解算成果的精度越低。为此,在布设GPS网点时应在满足规范要求的范围内尽可能的均匀分布,且已知点能够构成一定的图形强度(三角形或者多边形,且最小内角大于15°),对于解算未知点成果的精度有较强的保证。
四、实例分析
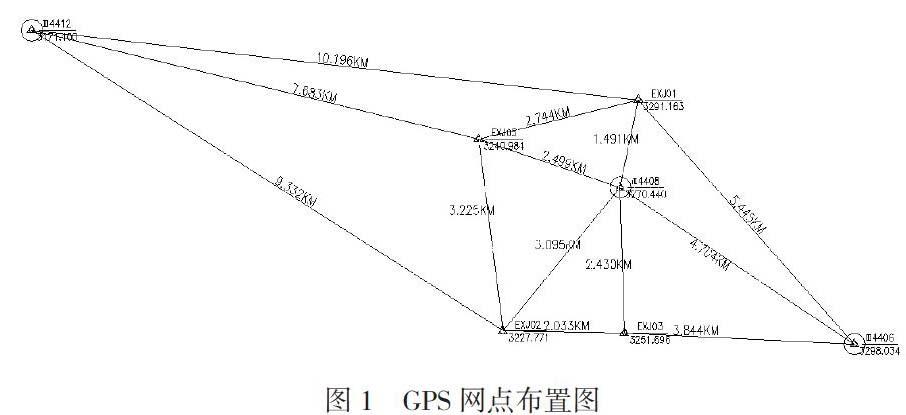
以西部某项目为例,需要布设E级控制网,解算结果为1980年西安国家坐标系,高程系统采用1985国家高程基准,采用高斯3°带投影。观测人员严格按照早做规范、作业指令进行操作,使用4台南方灵锐S82双频接收机,作业前通过检验站检测,性能和指标均符合要求。由于测区附近国家点人为破坏严重,加上风化等自然环境的影响,在测区找到3个控制点,且分布不均匀。如图1所示,EXJ01-EXJ05是测区布设的未知点,4406、4408、4412是已知的GPS控制点,它们的分布几乎成一条直线,且不均匀,4406和4408距离较近。
本次项目采用南方测绘GNSS数据处理软件进行基线处理、自由网平差、最小约束平差及约束平差,为了检验起算数据的精度,进行如下数据处理:
(1)进行自由网平差。平差结果显示:XJ05点的自由误差最小为0.014m,高程为3245.919m;XJ02点的自由误差最大为0.027m,高程为3182.535m。
(2)用控制点4412、4408、4406进行约束平差。平差结果显示:XJ05点的自由误差最小为0.031m,高程为3290.542m;XJ02点的自由误差最大为0.031m,高程为3227.154m。
(3)用控制点4412、4408进行平差。平差结果显示:XJ05点的自由误差最小为0.014m,高程为3291.163m:XJ02点的自由误差最大为0.021m,高程为3227.771m。
通过数据对比分析,我们发现用两种方法进行约束平差时,控制点的平面位置拟合较好,但高程变化较大,说明起算数据平面匹配较好,高程匹配精度较差。同一个未知点两次平差结果高程最大变化量0.621m,而高程中误差最大值为0.031m,说明高程拟合的中误差存在粗差(或者是错误),不能很好的表示实际起算数据高程之间的拟合精度。基于此,我们有必要对GPS高程拟合的中误差的可靠性进行探讨和分析。通过数据分析,进行高程拟合时,距离已知控制点越远高程变化量越大。同一个点两种方法高程拟合最大变化量是0.621m,而最大中误差只有0.031m,此时的中误差已经不能反映该点的实际精度。
由于只有3个起算数据,没有多于的起算数据判定具体哪个起算数据的高程有问题来剔除粗差点,然而我们可以通过高程拟合变化规律和理论分析得出结果。
五、结语
通过以上的论述,我们得出:
(1)GPS高程拟合时,若控制点只有3个,且有一个起算点高程数据不准确,GPS的高程误差就会在不准确起算数据方向两侧逐渐增大。这是由于3个起算数据可以确定一个高程基准面,若一个起算数据高程不准确,则相当于把正确的高程基准面倾斜,距离不准确点越远,高程变化量越大。
(2)高程拟合时,我们可以先进行自由网平差,在进行约束平差。若两种方法拟合成果变化量很小,则说明起算数据高程之间匹配较好;若差值变化量很大,则说明起算数据的高程精度匹配精度不高。这是由于自由网平差的高程成果相当于形成一个高程基准面,而约束平差相当于重新定义一个高程基准面,它们的高程成果在相对一个小区域内(≤10KM)理论是一个固定的差值。若这个差值变化量较大,则说明起算数据之间的高程匹配精度不高。
综上所述,在工程测绘的领域,平面拟合的中误差可以作为起算数据进行平面精度匹配的依據,而高程拟合的中误差不可靠。为此,建议在GPS工程控制网进行高程拟合时,条件允许的情况下尽量有5个或5个以上的起算点数据,且均匀分布在测区中。当联测点多于3个时,内业计算时可分组计算,选择符合条件较好的点作为起算数据,求得最优结算结果。
参考文献
[1] 刘基余.全球定位系统原理及其应用[M].北京:测绘出版社,1999.
[2] 张戈,王宇.GPS在工程测量中的作业方法[J].测绘通报,2000(03):33-41.
[3] 叶世榕.GPS非差相位精密单点定位[D].武汉:武汉大学,2002.
[4] 徐绍铨等.GPS测量原理及应用[M].武汉:武汉大学出版社,2007.
[5] 陈芳等.GPS测量误差中关于对流层延迟的探讨[J].西部探矿工程,2005(106).

