水体大气复氧系数计算公式研究综述
乔 丹
(杨凌职业技术学院陕西杨凌712100)
水体大气复氧系数计算公式研究综述
乔丹
(杨凌职业技术学院陕西杨凌712100)
水体中溶解氧的含量是表征水体生态功能的重要指标和控制性因素,其主要来源是大气复氧,因此水体大气复氧机理和影响因素是水体生态环境研究的重要课题,目前主要集中于水体大气复氧系数计算方面。本文通过对水体大气复氧系数计算公式的研究进行总结,概括了水体大气复氧系数计算方程的基本形式,并指出了它们的应用条件和存在问题。以期为今后其他学者研究水体大气复氧提供依据。
水体大气复氧;复氧理论;表面传质系数;复氧系数
1 水体大气复氧系数的研究意义与背景
天然水体都具有一定的自净能力,即受污染的水体通过物理、化学、生物等因素的作用,使污染物的浓度和毒性逐渐降低,并基本恢复或完全恢复到污染前的状态,从而保持水质良好。溶解氧的含量高低是衡量水体自净能力强弱的先决条件。天然水体中的溶解氧来源于大气复氧、绿色水生植物的光合作用以及外来水体携带的溶解氧,其中大气复氧是水体溶解氧的主要来源。增加水体中的溶解氧含量对于维持良好的水质及保持其正常的生态功能具有重要的现实意义。
水体的大气复氧是一个极为复杂的气液两相间的传质过程,至今有许多研究,提出了各种描述传质过程的理论模型,如双膜理论、溶质渗透理论、表面更新理论等,这些模型大都给出了传质系数KL的计算公式。但这些模型都建立在一定的假设条件基础上,具有一定的适用范围,对于天然水体而言具有局限性。模型当中的某些参数由于实验条件和科学技术的限制而无法获得。因此,将理论模型用于实际当中是有难度的。鉴于以上理论模型应用的局限性,一些学者针对未知气液两相接触面积a时的气液总传质系数K2,根据不同水力学条件和影响因素,提出了计算水体复氧速率系数的公式。
2 复氧系数K2计算公式
关于复氧系数K2的研究,大量学者利用原型或模型试验所得到的数据,根据其相关性,用回归分析或量纲分析等方法推导一个与实测数据相吻合的经验或半经验公式。这些公式大多以河流水力学特性为参数,其主要分为以下几组:
(1)以河流流速和水深为基本参数,这类计算公式的表达式如下:

式中:u为流速;H为水深;α为有量纲系数;x、y为常量指数。
国外有许多学者通过对天然河流中的溶解氧进行实地观测,最终拟合分析得到了复氧系数与平均流速和平均水深的关系式。但是,不同的学者是根据不同的河流实测值得到的结果,由于受河流特征、气候环境等因素的影响,没有哪个公式可以普遍的适用于所有的天然河流。Omole[1]对下列公式进行了比较:
笔者分别采用统计学方法和图表分析法对各公式进行比较,最终表明:误差最小,直观表示最佳的模型是O’Connor模型;表明根据多条河流的实测数据而得来的模型方程具有更好的拟合效果。
Omole和Longe等人[2]按相对似然的顺序对以上前10个模型进行排序。研究结果表明,不同季节的数据宜选用不同的模型方程。这进一步说明,这些公式只是针对于某一特定的环境条件和水流特征而得出的经验公式,并不具有普遍适用性。
(2)Melching和Flores[3]利用多个河段的复氧系数数据对K2的计算公式进行拟合。根据河流水流的流态将其分为两组:水流特性相对均匀的柱状流和浅滩。K2随流速增大而增大,随水深增大而减小,而流速和水深通常又随流量增大而增大,因此,随流量增大,流速和水深对K2的相对影响会变化。通过多元线性回归得到了以下的K2计算方程:
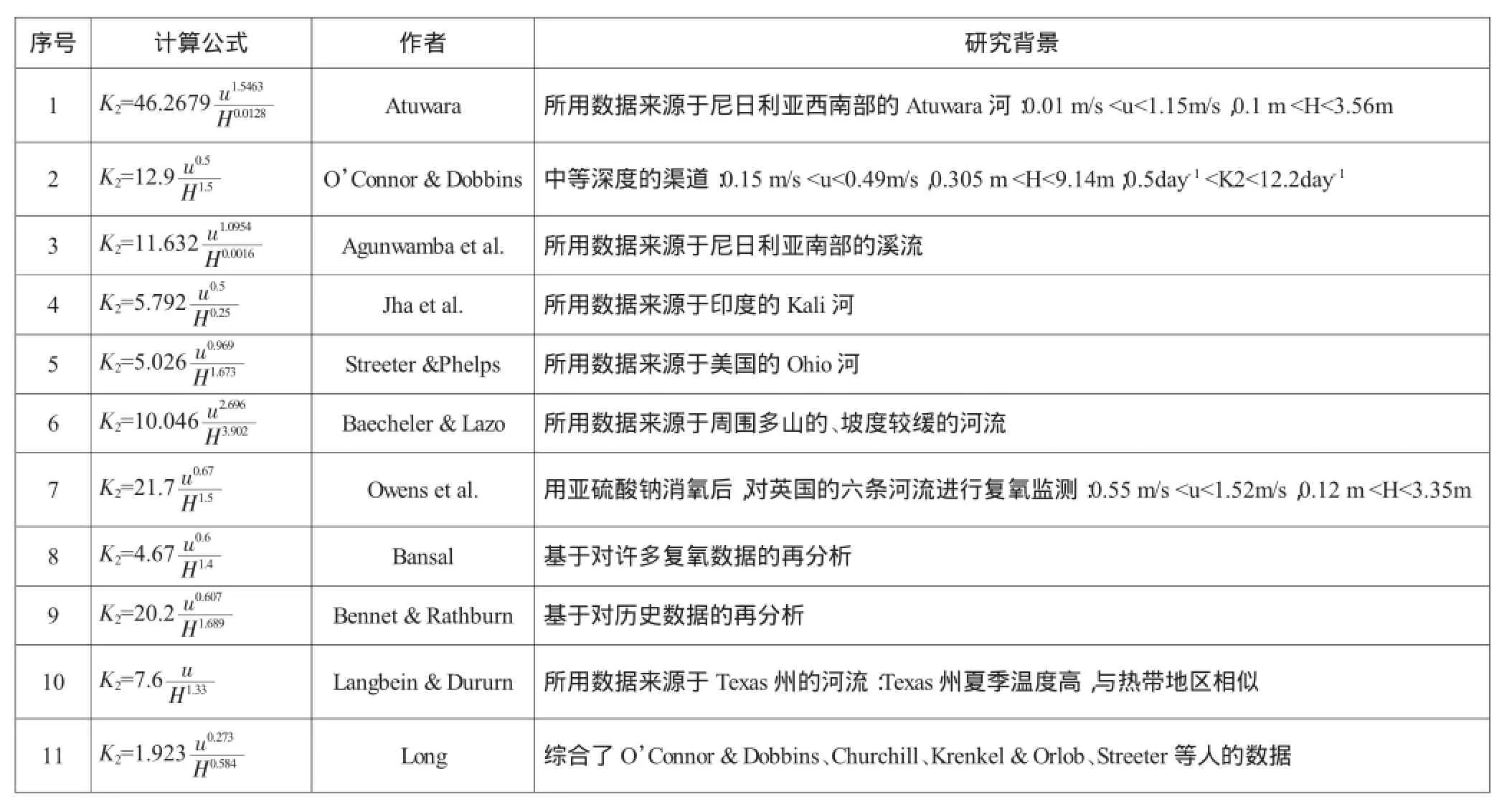
表1 以平均流速、平均水深为参数的复氧系数计算公式[1]

式中:u为平均流速;i为水面坡降;ui能量耗散率;H水深;W为水面宽度;复氧系数K2单位为day-1。
(3)描述河流水质的第一个模型是由H. Streeter和E.Phelps在1925年提出的,简称S-P模型,该模型给出的复氧系数K2计算公式为,u为流速,T为实测水温,R为水力半径,此公式计算结果较实测值偏小。因此,Agunwamba等人[4]根据在阿马迪溪(Amadi Creek)测得的一系列数据,通过多元回归分析,提出了新的复氧系数计算公式:

通过用一组独立的数据对该公式进行验证,结果表明,该公式的计算值可以与实测值达成很好的一致性。此公式与其他公式类似,实质上也是反映了复氧系数与河流几何参数、流速之间的关系。
(4)不同的弗劳德数Fr对应不同的水流流态,在Fr和流速越大的情况下,水流表面变得更加参差不齐,产生波浪,水流破碎程度加剧。在此理论基础上,早在1969年时,Thackston和Krenkel[5]根据在耗氧环境下宽为0.61m的水槽中所得的试验数据,通过非线性回归分析得出K2=24.9(1+Fr0.5)u*H-1.0,u*为剪切速度,适用条件为0.015m≤H≤0.091m。但是,在低Fr或者低流速和水面坡降的情况下,此公式对复氧系数有所高估。后来,笔者用其他一些学者的实测数据将上式进行重新率定,得出以下的率定公式[6]:K2=4.98(1+9Fr0.25)u*H-1.0。对于Fr适中的水流,原始方程对于K2的估算是准确的。但是,在低流速和低弗劳德数的情况下,校正方程对于K2的估算更加准确一些。
(5)以河流流速、水面坡降和水深为基本参数,这类计算公式的表达式如下:

式中:β为有量纲系数;i为水面坡降;x、y、z为常量指数。
(6)Dobbins基于薄膜渗透理论,结合自然河流中和Krenkel&Orlob实验水槽中的实验数据建立了如下的半经验公式[7]:
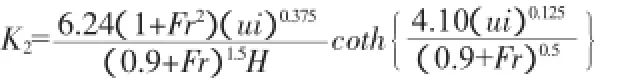
Dobbins基于能量耗散模型和分子扩散模型给出的半经验公式为:

(7)大多数学者给出的复氧系数估算公式都受到水动力条件和环境条件的限制。Gualtieri等人[8]考虑了除风速以外,影响K2的14个参数,即K2=f[H,u,W,ψ,Fr,g,i,u*,Q,v,Dm,Ts,n],其中:ψ为横断面的形状因子,Fr为弗劳德数,g为重力加速度,u*为剪切速度,,Ts为水表面张力,n为曼宁粗糙系数,gui为单位质量的能量耗散率,其他符号意义同前。通过无量纲分析,最终得到以下一组复氧系数K2的表达式:
Re和S的情况;
Gualtieri等人综合考虑了复氧过程当中多种影响因素的存在,给出了在忽略风速影响与温度恒定的情况下,矩形截面的水流的复氧系数表达式。该组表达式在推导过程中,始终紧密联系相关理论公式,使所得公式具有理论基础,能更好地适用于一般情况,不具有针对性。此组公式为以后学者研究复氧系数的定量表达式奠定了可靠的理论基础。
3 结论与展望
关于水体大气复氧系数计算,有不少学者已经进行了比较广泛的实验研究和实践,基本上可以得出以下几点结论:
(1)许多学者对自由液面传质系数(复氧系数)进行了大量的研究,成果较多。多以平均流速、平均水深、平均紊动强度、水面坡降和弗劳德数等作为参数来进行计算公式的推求。然而,这些公式都是根据一定环境条件和水动力条件下所测得的数据分析得来的,因此,没有哪一个公式对所有河流都有较好的适用性。即使是误差较小的公式,也可能忽略了一个或多个主要的影响因素。
(2)水体大气复氧是气液两相之间质量传递的一个较复杂的过程,涉及多个研究领域。目前已经进行了大量的复氧能力研究工作,具有了较好的基础。但是,就复氧系数的研究而言,考虑的影响因素还不够全面,计算公式的普适性较差。因此,在以后的研究中,应理论与实际相结合、大量采集各种条件下的监测数据,综合考虑多种影响因素,建立一个更加完善、更具有普适性的复氧系数计算方程,为实际工程提供可靠的预测分析。陕西水利
[1]Omole D O.Composite Goodness of Fit inReaerationCoeffcientModeling[J]. Environment&Natural ResourcesResearch,2012,2(3):71-83.
[2]Omole D O,Longe E O,Musa A G.An Approach to Reaeration Coefficient Modeling in Local Surface Water Quality Monitoring[J]. Environmental Modeling&Assessment,2013,18(1):85-94.
[3]Melching C S,Flores H E.Reaeration equations derived from US Geological Survey database[J].JournalofEnvironmental Engineering,1999,125(5):407-414.
[4]Agunwamba JC,Maduka C N,Ofosaren A M.Analysisof pollution statusof Amadi Creek and its management[J].Journal of Water Supply:Research&Technology-AQUA,2006,55(6):427-435..
[5]Thackston E L,Krenkel P A.Reaeration prediction in natural streams[J].1969.
[6]ThackstonEL,DawsonIIIJW. Recalibration of a reaeration equation[J]. Journal of environmental engineering,2001,127(4):317-321.
[7]雒文生,李莉红,贺涛.水体大气复氧理论和复氧系数研究进展与展望[J].水利学报,2003,11:64-72.
[8]GualtieriC,Gualtieri P,Doria GP. Dimensional analysis of reaeration rate in streams[J].Journalofenvironmentalengineering,2002,128(1):12-18.
(责任编辑:畅妮)
X143,TV131.2
A

