基于跳距与改进粒子群算法的DV-Hop定位算法*

范时平，罗丹，刘艳林

（重庆邮电大学通信与信息工程学院，重庆400065）

基于跳距与改进粒子群算法的DV-Hop定位算法*

范时平*，罗丹，刘艳林

（重庆邮电大学通信与信息工程学院，重庆400065）

针对DV-Hop定位算法定位精度不高的问题，提出一种带改进的权重平均每跳距离与改进的粒子群算法以改进经典DV-Hop算法。一方面，提出跳距误差与估计距离误差的加权平均值，修正原始的平均每跳距离。另一方面，采用分段的指数、对数递减权重改进粒子群的权重；同时，结合人工鱼群位置更新的优点来改进粒子群算法的位置更新。用改进的粒子群算法求解未知节点坐标，以提高定位精度。实验仿真表明，该算法的定位精度和稳定性与其他算法相比有明显的改善。

无线传感器网络；Distance Vector-Hop Algorithm；改进的粒子群算法；平均每跳距离

EEACC：7230doi：10.3969/j.issn.1004-1699.2016.09.020

无线传感器网络是由大量廉价、小体积、能量及通信能力有限的无线传感器节点以自组织方式组成的网络，已被广泛应用于国家防卫、环境监测、目标跟踪定位、生产安全等领域［1］。节点定位技术是无线传感器网络应用的基础和关键技术之一，具体体现在无线传感器网络主要工作是在指定区域执行各种监测任务，位置信息对传感器网络的监测至关重要，事件发生位置或者获取信息节点位置是传感器节点监测消息中包含的重要信息，位置信息的准确性直接影响传感器节点采集数据的有效性［2］。因此，只获取节点监测的数据而不知该节点的位置信息是毫无意义。

目前，无线传感器网络定位算法［3-6］分为基于距离（Range-based）定位算法和基于距离无关（Rangefree）定位算法。基于距离的定位精度相对于无需测距定位精度高但需要额外的硬件设施，成本高，不适合大规模网络；无需测距定位算法，其精度相对低，但无需测距定位具有低能耗，通信开销小、无需硬件设施支撑以及成本低等优势，因此无需测距定位更适合大规模网络以及未来的发展。

DV-Hop定位算法目前仍然处于研究阶段，现已有大量文献对其进行研究。文献［7］提出采用加权思想计算未知节点的平均每跳距离，能够提高DV-Hop定位算法的精度；文献［8］采用网络中信标节点的最小与最大的平均每跳距离作为所有未知节点的平均每跳距离，实验结果表明能提高精度。其次，由于最小二乘求解未知节点坐标存在误差，文献［9-11］提出在DV-Hop算法的未知节点求解坐标阶段利用改进的粒子群算法代替传统的最小二乘法估计未知节点坐标；文献［12］提出首先采用离散粒子群算法选出一组最优的信标节点，然后再采用粒子群算法求解未知节点坐标，虽然采用此方法能提高精度，但是网络节点密度过大。在上述文献中，它们都是分别从第二阶段和第三阶段改进DV-Hop算法，而文献［13］中指出DV-Hop定位算法中的信标节点的平均每跳距离具有较大的误差，而定位需要依赖于平均每跳距离。针对现有的不足，本文将从两方面进行研究，首先对平均跳段距离优化，其次采用改进的粒子群算法求解未知节点的坐标。

1　DV-Hop定位算法及其误差分析

1.1经典DV-Hop算法介绍

1.1.1计算最小跳数

信标节点向其他节点广播初始化跳数为0以及其他信息（位置信息），其他节点记录同一信标节点最小跳数信息并将跳数加一后转发给其他节点，最后求得每个信标节点到未知节点的最小跳数。

1.1.2平均跳距的计算

经过第一阶段后，整个网络知道信标节点与信标节点和未知节点之间的最小跳数，网络中信标节点的平均每跳距离按下式计算：

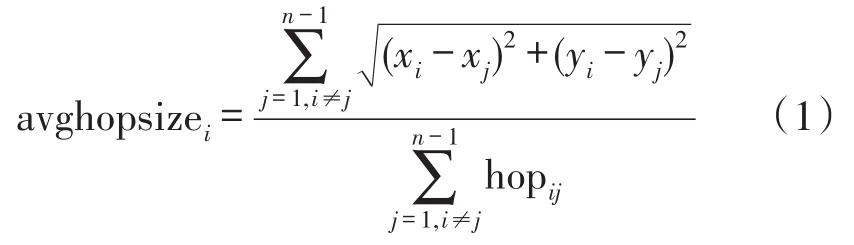
其中，n为信标节点的个数，（xi，yi）、（xj，yj）分别为信标节点i、j的坐标，hopij为信标节i、j之间的跳数。

1.1.3未知节点的估计

假设未知节点k的坐标为（xk，yk）和信标节点i的坐标为（xi，yi），未知节点k到信标节点i间的距离采用式（2）计算

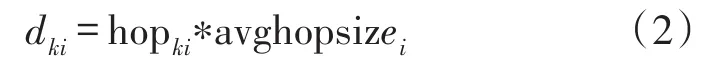
网络中所有未知节点到信标节点的距离采用式（2）计算。

传统的DV-Hop定位算法利用最小二乘法估计未知节点坐标，如下式：

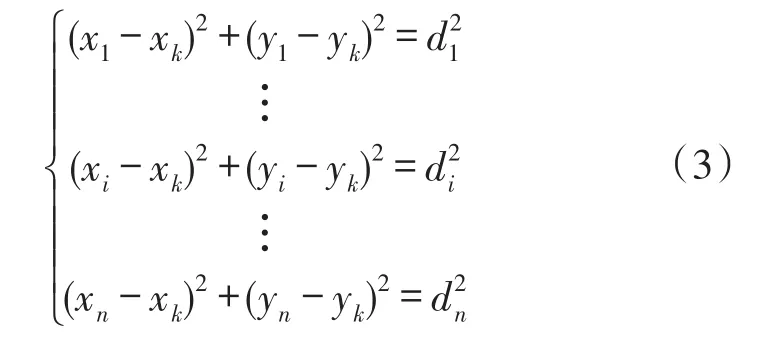
上式利用前n-1项分别减去第n项可转化最小平方差估计未知节点坐标

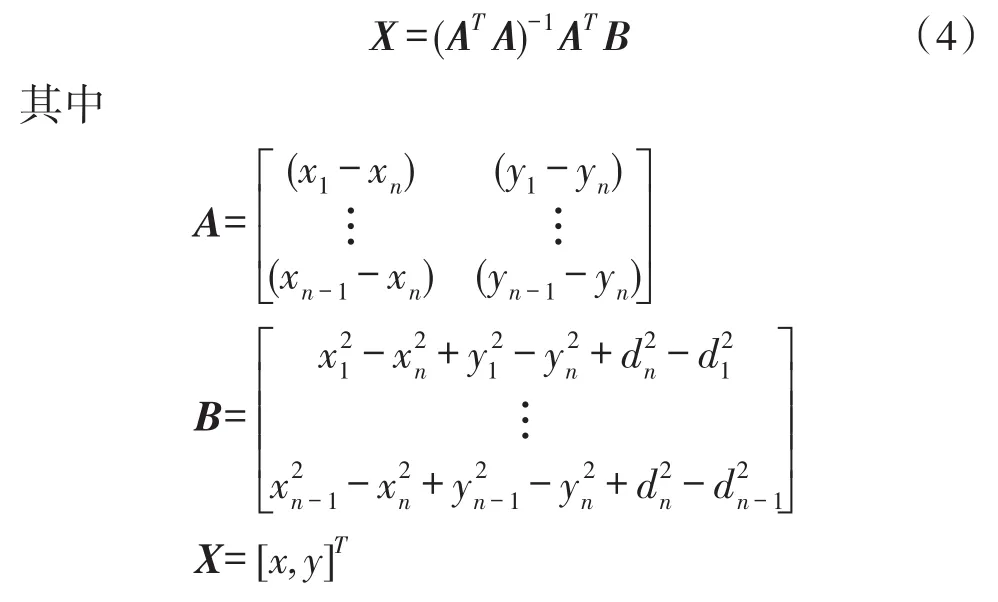
1.2DV-Hop定位算法误差分析

影响无线传感器网络定位精度较低的原因很多，但主要原因有节点非均匀分布、DV-Hop定位算法自身因素。本文分别从以下几个方面进行分析：

（1）无线传感器网络中的节点一般由飞机抛洒节点，网络中的节点通常呈非均匀分布。因此，网络中平均每跳距离有较大的差异。其次，传统的DV-Hop算法利用信标节点间的直线距离和跳数计算平均跳距，但信标节点间的最小跳数经过的距离是折线。如图1所示：假设节点通信半径为15 m，信标节点A、B之间真实距离为22 m而在DV-Hop算法中平均每跳距离利用式（1）计算，计算得到的平均每跳距离约为7.33 m，但实际平均每跳距离约为9.33 m，所以传统的DV-Hop算法计算的平均每跳距离会产生很大的误差。

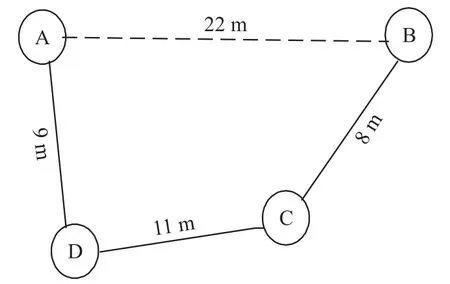
图1　两信标节点间部分拓扑关系

（2）传统的DV-Hop算法直接利用第二阶段计算的平均跳距作为未知节点到信标节点的每跳距离，这样计算的未知节点到信标节点的距离会产生极大误差，若不对第二阶段的平均每跳距离误差处理必会对后面的计算产生影响；同时，由于最小二乘法本身存在计算误差，未知节点的估计位置会受累计误差的影响，导致传统DV-Hop定位精度不高。

针对上述存在的问题提出改进，首先利用加权的思想改进平均每跳距离。其次，最小二乘法计算本身存在误差以及无效信标的存在，在估计未知节点坐标时利用改进的粒子群算法代替最小二乘求解未知节点坐标。

2　本文的优化算法

本文对信标节点的平均每跳距离和粒子群算法进行优化，因此，分别从这两方面提出改进。

2.1改进的平均跳距

DV-Hop的主要误差是由平均每跳距离引起，本文引入平均每跳距离均方加权误差的思想对信标节点平均每跳距离进行优化。具体步骤如下：

第1步假设网络中有n个信标节点，计算所有信标节点的平均每跳距离，并记为avg，则有

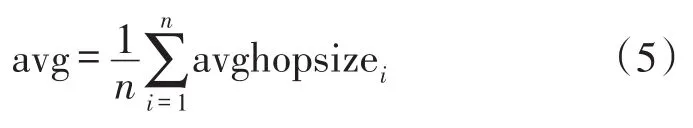
第2步利用信标节点i的平均每跳距离与所有信标节点的平均每跳距离之差计算误差Di1，如下式：

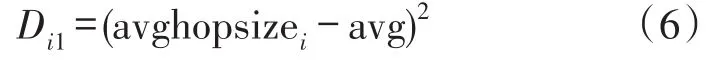
第3步由于节点间的估计距离利用式（2）计算得到，容易产生累积误差。因此，节点间的估计距离也是评判信标节点平均每跳距离是否精确的另一标准。利用信标节点i、j间的实际距离与其估计距离间的平均每跳距离误差Di2下式计算：

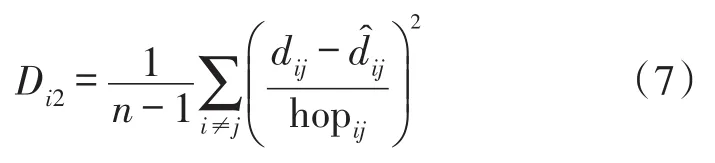
其中，dij为信标节点的实际距离，dˆij=avghopsizei· hopij为信标节点i、j的估计距离。

第4步综合考虑信标节点i的平均每跳距离误差，得到自身平均每跳距离误差系数，并把此误差系数作为其余信标节点计算平均每跳距离的权值，权值计算表达式为：

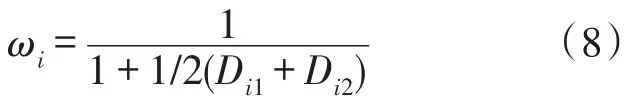
第5步重新估算信标节点i的平均每跳距离avginew，由于均方误差差越小，则真实度越高，相应的权值越大。本文提出采用带加权值方法优化信标节点i的平均每跳距离。计算信标节点i的平均每跳距离方案如下：

①信标节点i、j两节点间的平均每跳距离为avghopsizeij即：

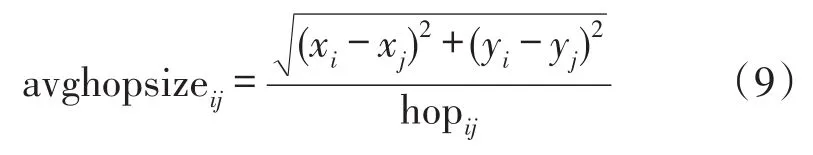
②改进的信标节点i的平均每跳距离为信标节点i与其余m-1个信标节点的平均每跳距离的加权，即

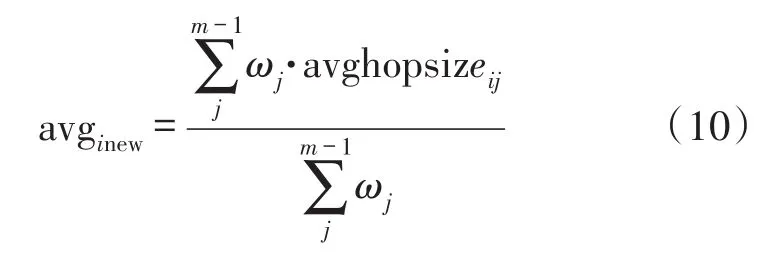
2.2改进的粒子群算法

粒子群优化算法是由Eberhart和Kennedy博士提出的新型智能算法。粒子群优化算法与其他智能算法相比，它具有简单，易实现以及较强的优化能力。粒子群算法的数学描述如下：假设种群数为N，每个粒子i包括一个D维坐标和速度向量Xi=（xi1，xi2，…，xiD），Vi=（vi1，vi2，…，viD）；ω为惯性权重，粒子i的历史最优位置pbesti=（pbesti1，pbesti2，…，pbestiD），全局历史最优位置gbesti=（gbesi1，gbesi2，…，gbesiD）；c1、c2加速因子（一般取2），r1、r2为在［0，1］上服从均匀分布的随机数，r为约束因子，速度和位置更新如下式：

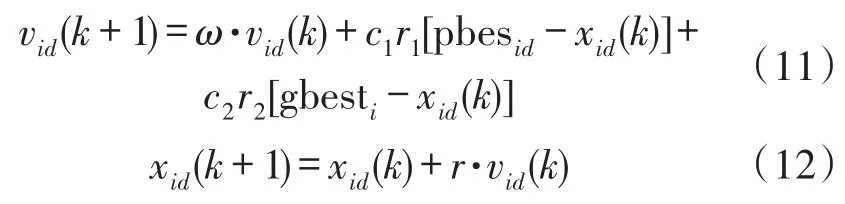
虽然粒子群优化算法具有较强的全局搜索能力，且初期收敛较快，但在后期由于粒子的速度减小慢，导致位置变化慢，所以粒子群容易陷入早熟和收敛慢等问题，这样粒子就难以跳出局部最优解。针对此问题分别优化粒子群的惯性权重和变异步长，以给后期搜索时提供多样化的解空间。

2.2.1权重的改进

惯性权值会影响粒子的全局搜索能力与局部搜索能力之间的平衡，即使用较大的惯性权值，算法具有较强的全局搜索能力，较小的权值有利于局部搜索能力和加速算法的收敛。根据上述思想，本文提出采用指数递减与随机对数递减分段的惯性权值。这样做的好处在于，搜索初期具有较大的权重可以得到较大的解空间，采用此方法可以使得到的粒子具有多样性；在搜索中后期，利用随机对数递减惯性权值不仅有利于加快算法收敛速度，而且更有利于增大局部解的多样性，在一定程度上使粒子跳出局部解，从而提高粒子群算法的效率和精度。k为当前迭代次数，K为总的迭代次数，设ωmax=0.9，ωmin=0.4，如图2所示，k小于60时，采用递减的指数权重；k大于60时，采用随机对数递减权重。

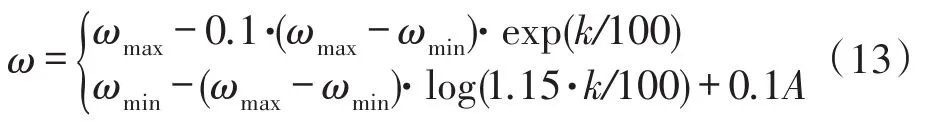
其中A=0.5·rand（）。

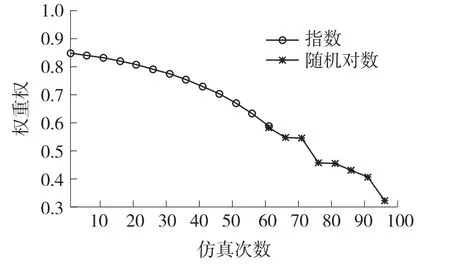
图2　权重与迭代次数图

2.2.2改进的位置更新

在后期为了使算法更快速有效达到收敛，跳出局部解。人工鱼群算法中鱼群觅食、聚群、追尾阶段等行为中的位置更新具有较大的随机性［14］，因此可以增加解的多样性，并跳出局部解等优点。因此，本文采用人工鱼群的位置更新进行改进粒子群的位置更新。改进粒子的位置更新采用下式计算：

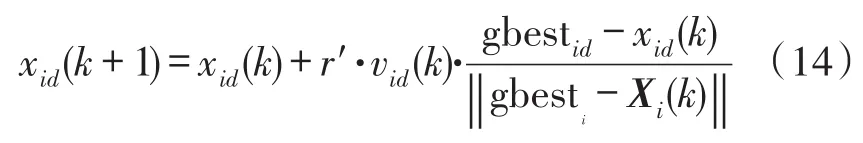
其中r′=1+0.3·rand（）

2.2.3适应度函数

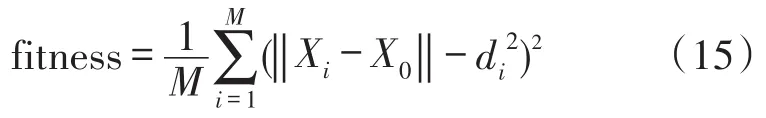
其中M大于等于3，为未知节点选用信标节点的数目；Xi为信标节点的坐标；X0选用粒子群算法中的全局最优解；di为未知节点与信标节点i计算的距离。

3　本文的算法步骤

①初始化相关参数。包括：网络区域大小、网络中的节点数、节点跳数。

②利用DV-Hop算法的第一、二阶段获得每个信标节点与未知节点的最小跳数和信标节点i的平均每跳距离。

③利用改进的平均每跳距离的方法重新计算信标节点的平均每跳距离，即根据式（5）～式（10）计算avginew，代替原始的平均每跳距离avghopsizei。

④初始化种群。初始化粒子i的位置Xi=（xi1，xi2，…，xiD）与速度Vi=（vi1，vi2，…，viD），自身历史最优位置pbesti=Xi，根据式（15），计算种群的适应度函数值，全局最优gbesti为初始种群的最有位置，并初始化k=0。

⑤令k=k+1。根据式（11）～式（14）更新粒子的速度和位置。

⑥比较当前位置与粒子历史最优位置的适应度值的大小。若当前位置粒子的适应度值比粒子历史最优位置适应度值，则更新粒子历史最优位置；否则，保持粒子历史最优位置。

⑦比较粒子历史最优位置与全局最优位置的适应度值的大小。若粒子历史最优位置的适应度值比全局最优位置的适应度值大，则更新粒子的全局最优位置；否则，保持粒子的全局最优位置。

⑧若满足终止条件，则输出全局最优解。否则重复执行步骤⑤～步骤⑦。

4　实验与仿真

4.1实验环境和参数设置

在Windows7的MATLAB2010平台下进行仿真模拟实验。将100个传感器节点，随机部署在100 m×100 m的网络中，未知节点和信标节点分布如图3所示。假设所有传感器网络节点具有相同的通信半径R。为了证明本文算法BDV-Hop更具有优越性，选择经典DV-Hop定位算法、文献［8］中的IDV-Hop以及文献［10］中的IPSO-DVHop算法进行实验对比，粒子种群数最大为30，最大迭代次数100，粒子最大速度为4 m/s。每个未知节点的定位误差公式

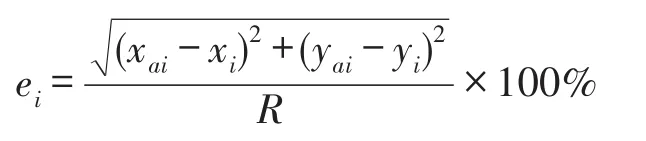
其中（xai，yai）是未知节点的真实坐标，（xi，yi）是未知节点的估计坐标，全网的定位性能估计采用归一化的相对误差公式计算，n为未知节点的个数，

图3　未知节点与信标节点的分布

4.2实验结果分析

4.2.1信标节点对定位误差影响

假设通信半径为30 m时，改变信标节点数目对定位性能进行仿真。本文算法与经典DV-Hop定位算法、IDV-Hop以及IPSO-DVHop进行对比，相应得到平均定位误差与信标节点数关系如图4所示。从图中得到定位误差随信标节点数目增加而减小，这是由于信标节点增加不但提高了跳距估计的准确性，而且降低了未知节点与信标节点之间因跳数过多而带来的积累误差。当信标节点数小于20时，定位误差受信标节点数目影响较大，信标数目大于20时，定位误差受信标数目影响较小，有趋于平稳状态。本文采用的算法分别比DV-Hop、IDV-Hop以及IPSO-DVHop的定位精度大约提高13.4%、8.2%、5.3%，且它的平均定位误差曲线更平滑，表明其稳定性更好。

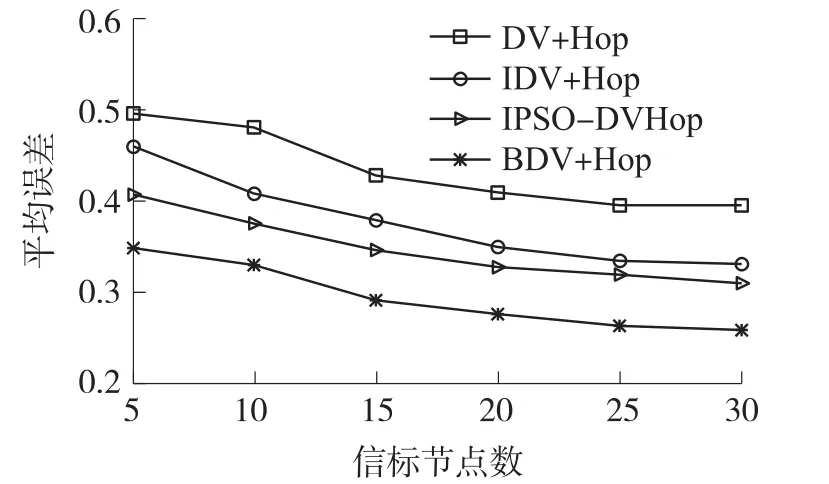
图4　定位误差与信标节点关系

4.2.2通信半径对定位误差影响

假设信标节点为20时，改变通信半径的情况下，从图中得到本文算法与其他3种算法相比具有更高的定位精度。如图5所示，通信半径在30 m以前，节点的定位误差随通信半径的增加呈减小的趋势。这是因为通信半径越大，节点的连通度越大，计算的平均每跳距离越精确；在30 m到40 m之间呈现出平滑的趋势；但当通信半径增加到40 m后，节点的定位误差有微小的上升趋势。这是因为通信半径增加到一定程度后信标节点的平均每跳距离有更大的误差，使定位精度下降。因此，通信半径并不是越大越好。总之，本文提出的算法优于其余三种定位算法。

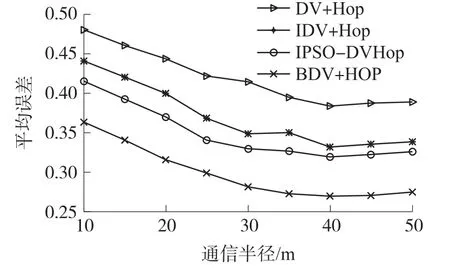
图5　定位误差与通信半径的关系

4.2.3定位稳定性分析

在网络区域为100 m×100 m的区域内，部署100个传感器节点，其中信标节点为20个，并固定通信半径为30 m。分别对经典DV-Hop定位算法、IDV-Hop、IPSO-DVHop以及本文算法进行20次仿真，得到平均归一化误差。从中得出本文采用的改进方法比其余3种算法的平均归一化误差与方差都要小，其稳定性更好。

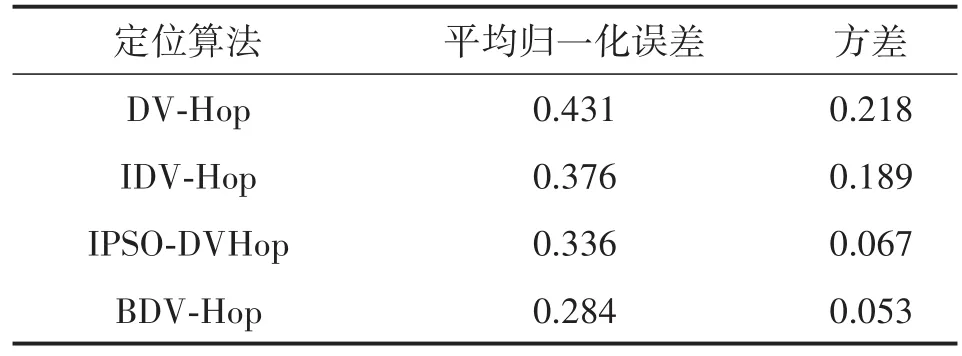
表1　定位算法的平均归一化误差与方差

5　结束语

本文通过介绍传统DV-Hop算法，并分析其主要误差来源，针对此误差提出采用平均每跳距离误差加权方法修正信标节点的平均每跳距离，并结合改进的粒子群算法求解未知节点坐标，以综合提高定位精度，通过MATLAB仿真实验，并得出实验结果。实验结果表明，在固定通信半径，改变信标节点数目的情况下，定位误差随信标节点数目增大而减小且本文的算法优于其他三种算法；在通信半径可变的情况，也得出了相应的结论。由此可知，本文的算法能提高定位精度。但是，采用粒子群算法增加了计算复杂，使网络计算开销增大。因此，高精度低复杂度的算法待进一步研究。

［1］彭宇，王丹.无线传感器网络定位技术综述［J］.电子测量与仪器学报，2011，25（5）：389-399.

［2］李晓维，徐勇军，任丰原.无线传感器网络技术［M］.北京：北京理工大学，2007：191-194.

［3］Rudafshani M，Datta S.Localization in Wireless Sensor Networks［C］//Information Processing in Sensor Networks，2007.IPSN 2007.6th International Symposium on.IEEE，2007：51-60.

［4］刘士兴，黄俊杰，刘宏银，等.基于多通信半径的加权DV-Hop定位算法［J］.传感技术学报，2015，28（6）：883-887.

［5］程秀芝，朱达荣，张申，等.基于RSSI差分校正的最小二乘-拟牛顿定位算法［J］.传感技术学报，2014，27（1）：123-127.

［6］Han G，Xu H，Duong T Q，et al.Localization Algorithms of Wire⁃less Sensor Networks：A Survey［J］.Telecommunication Systems，2013，52（4）：2419-2436.

［7］Fu C，Qian Z，Ji G，et al.An Improved DV-Hop Localization Algo⁃rithm in Wireless Sensor Network［C］//Information Technology and Applications（ITA），2013 International Conference on.IEEE，2013：13-16.

［8］Hadir A，Zine-Dine K，Bakhouya M，et al.An Improved DV-Hop Localization Algorithm for Wireless Sensor Networks［C］//Next Generation Networks and Services（NGNS），2014 Fifth Interna⁃tional Conference on.IEEE，2014：330-334.

［9］刘志坤，刘忠，唐小明.基于改进型粒子群优化的节点自定位算法［J］.中南大学学报（自然科学版），2012，43（4）：1371-1376.

［10］裴祥，李巧君.基于改进粒子群优化算法的无线传感器网络定位［J］.计算机与现代化，2015（7）：81-84.

［11］王亚子，杨建辉.改进粒子群算法的无线传感器网络节点定位［J］.计算机工程与应用，2014，50（18）：99-102.

［12］曹欲晓，严奎，徐金宝.一种最优锚节点集合上的两重粒子群优化DV-Hop定位算法［J］.传感技术学报，2015，28（3）：424-429.

［13］Zine-Dine K，Hadir A，Madani A，et al.Comparative Study of Lo⁃calization Algorithms Performance in Wireless Sensors Network［J］.International Journal of Research in Engineering&Ad⁃vanced Technology，2014：1-9.

［14］Neshat M，Sepidnam G，Sargolzaei M，et al.Artificial Fish Swarm Algorithm：A Survey of the State-of-the-Art，Hybridization，Combi⁃natorial and Indicative Applications［J］.Artificial Intelligence Re⁃view，2014，42（4）：965-997.

范时平（1970-），男，硕士，副教授，主要研究方向为无线传感器网络、嵌入式系统；

罗丹（1991-），女，硕士研究生，主要研究方向为无线传感器网络，1097342405@qq.com；

刘艳林（1990-），女，硕士，硕士研究生，主要研究方向为大数据。

DV-Hop Localization Algorithm Based on Hop-Size and Improvement Particle Swarm Optimization*

FAN Shiping*，LUO Dan，LIU Yanlin
（College of Communication and Information Engineering，Chongqing University of Posts and Telecommunication，Chongqing 400065，China）

In order to solve DV-Hop low localization accuracy，a novel localization method based on modified weighted average hop-size and improved particle swarm optimization algorithm is proposed.On the one hand，weighted average both hop-size error and estimated distance error modify initial average hop-size.On the other hand，index and logarithmic decrement of piecewise function improve inertia weight of PSO.Furthermore，combin⁃ing with localization update of Atificial Fish Swarm Algorithm improve PSO’s localization update.Then，improved algorithm estimate unknown node coordination.The experiment shows localization accuracy and stability of the method is greatly improved.

wireless sensors networks（WSN）；DV-Hop Algorithm；improved particle swarm optimization algorithm（PSO）average hop-size

TP393

A

1004-1699（2016）09-1410-06

项目来源：基于物联网技术的呼吸、脉搏异变及跌落的实时监测与报警的关键技术研究项目（61171190）

2016-03-14修改日期：2016-04-07