徒步导航系统中的自适应步态优化检测方法研究*
孙伟,丁伟,李瑞豹
(辽宁工程技术大学测绘与地理科学学院,辽宁阜新123000)
徒步导航系统中的自适应步态优化检测方法研究*
孙伟*,丁伟,李瑞豹
(辽宁工程技术大学测绘与地理科学学院,辽宁阜新123000)
针对步态检测的可靠性和准确性成为制约个人徒步导航定位系统高精度定位的主要因素,提出一种基于K均值聚类参数调整的自适应步态检测算法。首先研究行走过程的足部运动规律,并分析惯性测量单元输出加速度和角速率的数据特征,提出采用比力幅值滑动方差作为检测依据的步伐检测方案;分析滑动方差窗口参数、初始检测阈值参数和误检修正时间参数对于检测结果的影响并指出三者的关系,确定窗口参数、初始阈值选择的一般准则以及利用K均值聚类自适应确定时间参数以纠正初始检测结果中误检步态的可行性。利用实验室现有MEMS传感器开展了5组不同状态下的徒步实验,实验结果验证了步态检测算法的可行性和有效性。
人员定位系统;步态检测;滑动方差;K均值聚类;自适应
EEACC:7120;7230M;7320Edoi:10.3969/j.issn.1004-1699.2016.09.016
徒步导航系统是一种典型的个人连续定位系统,根据加速度计、陀螺仪输出信息研究行走过程的运动规律进而推算行人的实时位置[1-3]。MEMS惯性技术的发展推动了徒步导航技术的发展并为其实现工程化提供保障。人员定位系统可根据其特有步态规律实施步态检测算法区分步态静止阶段和摆动阶段,对静止步态阶段应用零速修正算法及时修正器件漂移引起的位置误差[4-5]。因此步态检测结果的有效性和准确度将直接影响定位结果的可靠性和精度,国内外学者以提高检测结果的准确度为目的开展了大量的研究工作并提出了多种检测方法。利用的检测量包括比力模值、比力滑动均值、比力滑动方差、角速度模值、角速度滑动均值、角速度能量等一种或多种相结合,检测涉及的参数包括滑动方差窗口大小、检测阈值以及同一步态持续时间长短[6-9]。已有检测算法大都基于特定的步态环境,检测参数大小固定,对不同个体、不同运动环境适应性较差。本文提出一种以比力滑动方差为检测量,结合MEMS器件数据特点确定窗口参数和阈值参数,利用聚类方法自适应的确定时间参数并纠正初始分类结果,取得较为理想的测试结果。
1 步态规律分析
1.1传感器安装位置的确定
一个完整的步态周期包括脚跟离地HO(Heel Off)、脚尖离地TO(Toe Off)、脚跟着地HS(Heel Strike)、脚尖着地TS(Toe Strike)4个过程(图1)[10]。其中TS至HO为静止阶段,其余各状态构成摆动阶段。静止阶段脚的速度理论上应当为零,对应于IMU输出比力应等于当地重力加速度,角速度为零。但实际情况由于器件偏差及测量误差的存在,IMU输出与理想值存在偏差,进而导致惯性解算脚的实际速度不为零。步态检测的目的就是辨识人行走周期中的静止阶段,是零速修正得以实施的前提。
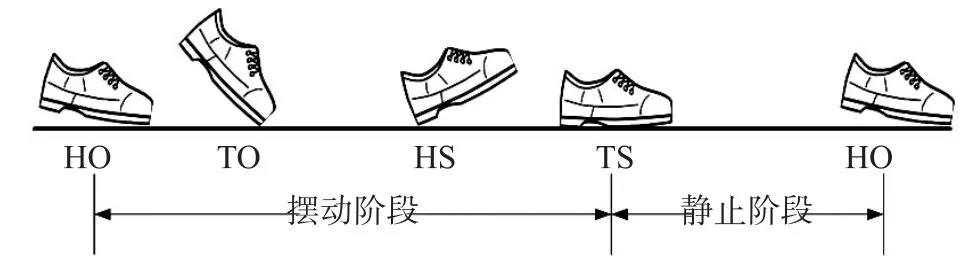
图1 步态示意图
徒步导航系统中的惯性测量单元IMU(Inertial Measurement Unit)安装位置各有不同,如安装在鞋跟侧面、鞋底中央、鞋面[8-9,11]。依据如上分析,将传感器安装于鞋面时可以获得最长的静止时间,可为零速修正提供充足的执行时间,因此,本文将MEMS安装于鞋面(图2),并定义载体坐标系(b系)的xb沿传感器纵轴指前,yb沿传感器横轴指左,zb与xb、yb构成右手空间直角坐标系指天。

图2 系统结构图
1.2步态特征提取
为寻求最优判别依据,进一步确定步态变化对于惯性器件输出数据的影响,截取某次测试后的惯性器件输出进行比对分析(如图3)。

图3 行走过程IMU输出
可以看出,足部静止阶段三轴加速度计输出及三轴陀螺仪输出都保持较长时间的稳定状态,但是3个正交方向的角速度近似为零,由于IMU安装角的存在导致重力分量作用于xb轴、yb轴加速度计导致加速度分别稳定于3个固定值;足部摆动阶段的数据波动变化较为剧烈,三方向加速度变化规律类似,而三方向角速度中y轴变化幅度显著大于其余两轴,这与人行走过程中足部运动规律及IMU传感器坐标轴指向对应。
步态检测用于判别行走过程中足部是否完全处于静止状态。因此步态检测算法可转化为模式识别问题,且检测结果仅有0、1两种状态(0表示静止,1表示运动)[12-13]。检测量的选择是步态检测的前提,不同检测量具有不同的数据特征,检测结果的有效性和准确率也有所区别。考虑MEMS加速度计性能比MEMS陀螺性能稳定、精度高[14-15],且由图3可知行走过程仅一个方向陀螺数据变化明显,因而选取加速度计输出构造检测量。
采用加速度幅值|fb|作为检测量,通过选择适当检测阈值可实现步态的辨识,但是通过对图4加速度幅值数据分析可发现,足部摆动阶段加速度幅值波动大,这将导致检测结果中摆动阶段出现许多错误的短时静止状态,易导致步态误判现象的出现。
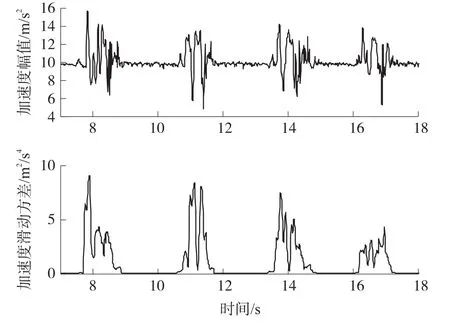
图4 加速度幅值与滑动方差
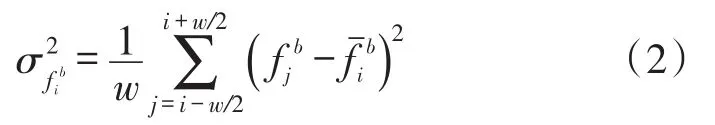

则步态(Gait)检测结果可表示为:

其中,σGate表示方差阈值。
2 自适应步态优化检测
步态检测涉及计算加速度滑动方差的窗口大小、判断静止状态的加速度方差阈值、误检纠正的时间参数。根据图5所示的检测流程可以看出,初始步态检测直接由加速度计数据通过选择适当窗口参数和方差阈值得到初始静态及动态。根据初始检测结果对误检步态的进一步纠正以提高最终步态的准确性,时间参数的选取应用了K均值聚类方法,具有自适应性。
2.1窗口大小设定
窗口参数是计算加速度滑动方差的关键参数,窗口大小决定参与计算滑动方差的数据量,不同窗口大小内的滑动方差不同。为说明窗口参数的特征,分别取w=10、w=20、w=30、w=40计算加速度滑动方差(如图6),对比发现w过小时导致阈值范围小,容易出现摆动阶段被误检为静止,随着w的取值增大,滑动方差越平滑,可供选择的阈值范围越大。但窗口参数并不是越大越好,因为计算时采用中心点前后各w/2的数据,导航窗口长度产生一半的时间延迟,延迟时间取决于IMU采样率。此外,当窗口参数过大时将导致部分摆动时刻滑动方差过于平滑,通过缩小阈值的可选择范围,避免出现摆动状态漏检。
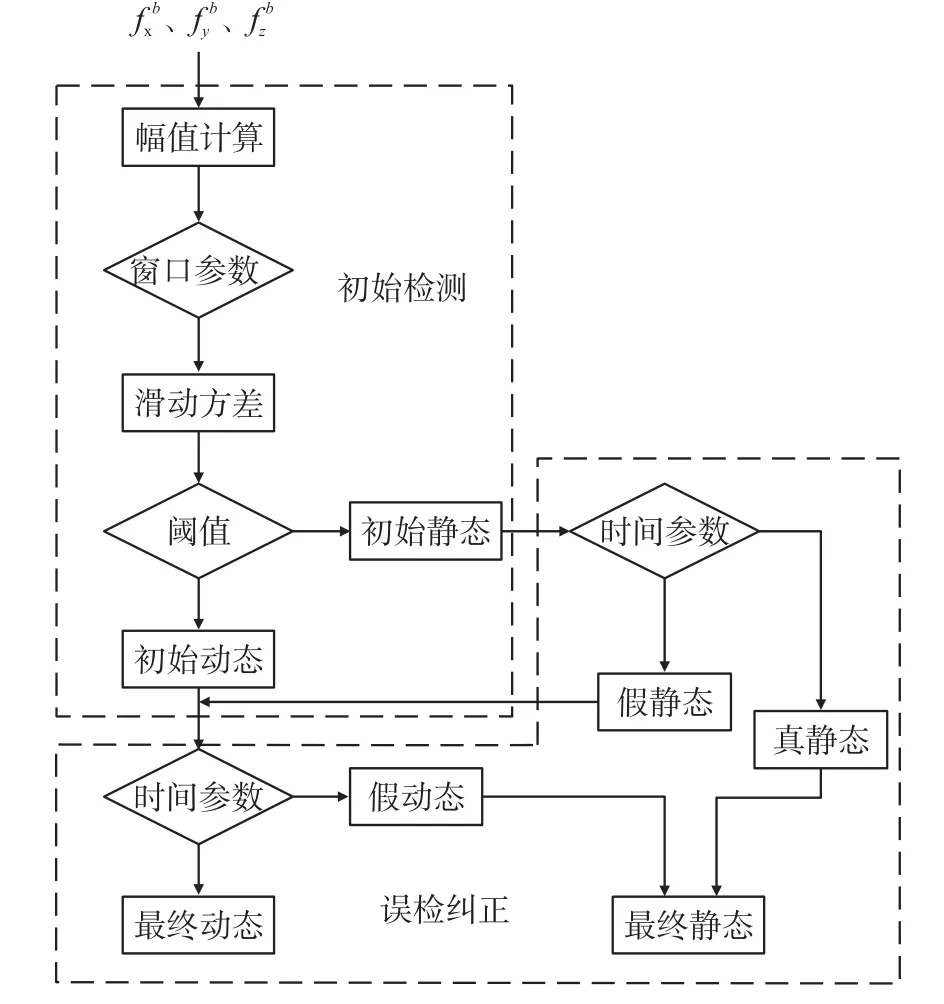
图5 自适应步态检测流程图
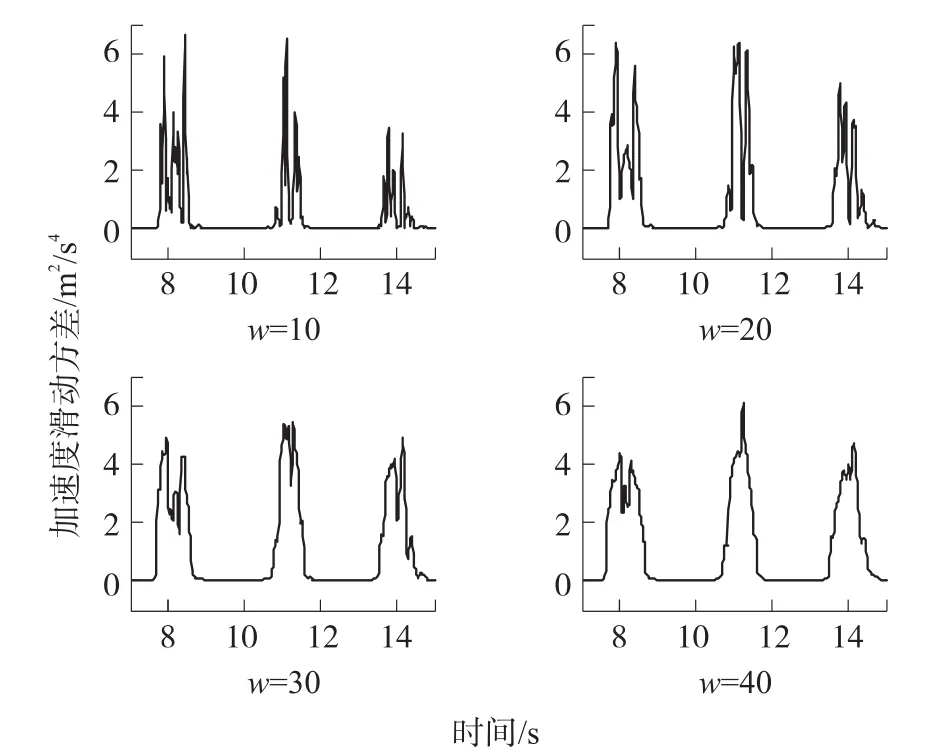
图6 窗口大小对加速度滑动方差的影响
2.2阈值设定
阈值是直接区分行人足部状态的核心参数,不同个体、不同行走速度的行走数据多对应的阈值参数各不相同,一般需要根据具体数据进行分析确定。通过对加速度滑动方差数据分析后发现:测量误差导致静止阶段滑动方差不为零,而是存在一些局部小幅度波动,同样摆动阶段也存在较大幅度波动。根据加速度滑动方差数据特点,阈值选择及对应的检测结果存在以下几种可能性:
③若取σ1<σGait<σ2,则不会漏检所有静态,但将出现部分摆动阶段被误检为短时静态。
④若σGait大于摆动低谷最大值小于摆动尖峰最小值,则步态检测退化为计步器,部分摆动阶段被误检为静态。
⑤若σGait大于所有摆动尖峰的最小值而小于摆动尖峰最大值,则将完全漏检部分摆动阶段,而相应时段被认为处于静态从而导致检测步数少于实际行走步数。
⑥若σGait大于所有摆动尖峰的最大值,则将漏检所有步态,检测步数为零,整个行走过程被视为静态。
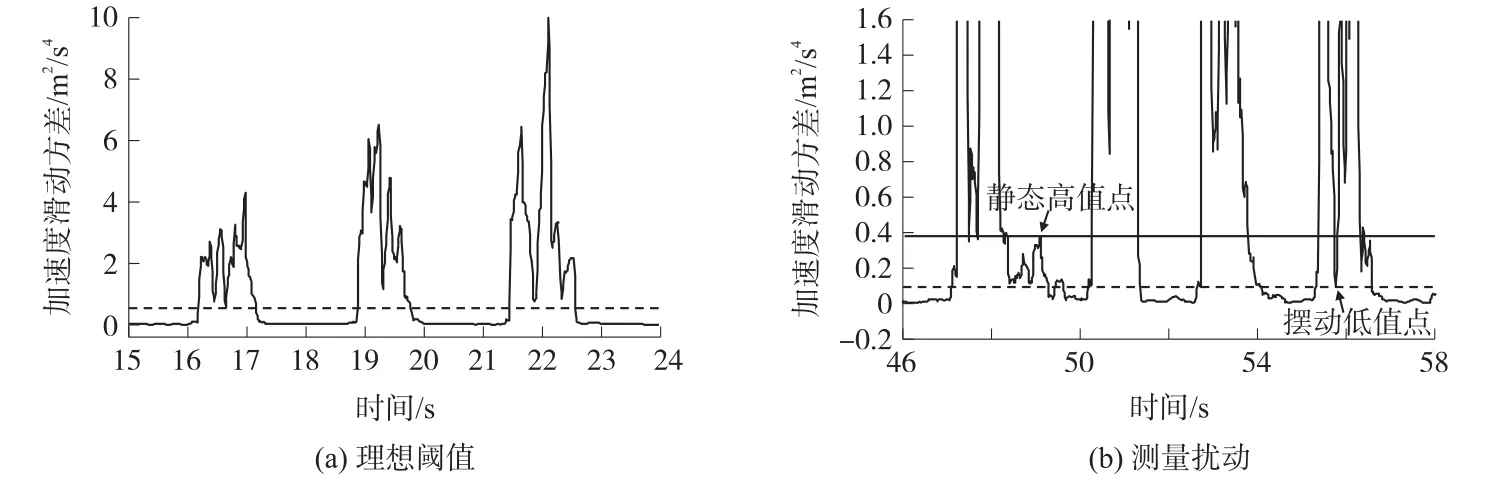
图7 阈值参数选取
2.3时间参数选取
通过对阈值参数的分析可发现阈值的准确选取较为困难,当出现图7(b)的情况时,无论怎样选择阈值都会产生误检并会出现与实际行走不符的短时静态或短时动态。为进一步提高步态检测方法的准确度,需对原始检测结果进行纠正,剔除不正确的步态结果。其中一种有效的方法是比较所有初始检测的静态阶段持续的时间,然后设置一时间阈值将所有小于阈值的短时静态阶段滤除。虽然该方法具有一定效果但可实现性差,原因在于时间参数选取存在困难,且不恰当的选取可能导致纠正结果呈现更大的偏离误差。
通过实现时间参数的自适应选择,可分别计算初始检测静态和动态的每一阶段持续时间,然后利用K均值聚类方法根据静态统计结果分为真、假静态。那么任何界于假静态持续最长时间和真静态持续最短时间之间的时间参数都可被准确区,并可实现对初始摆动的统计结果进行处理。具体实现过程如下:
①统计初始检测步态各次静态、摆动出现的时刻。对初始步态G作一次前向差分:
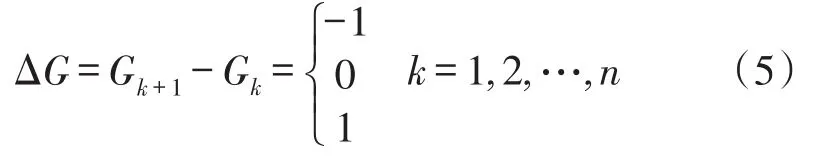
设定0表示静态,1表示摆动,因此式(5)中ΔG=-1即由摆动转为静态,ΔG=1为由静态转为摆动,ΔG=0则表示状态保持不变。记静态开始时刻(也即动态结束时刻)为tstance,动态开始时刻(也即静态结束时刻)为tswing,则有:
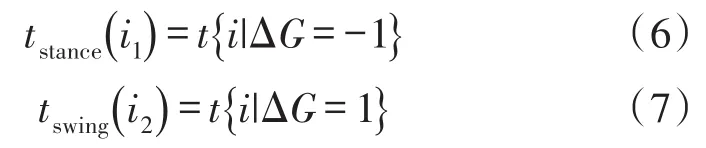
②分别根据tstance和tswing统计各次静态和动态持续时间内数据长度,记各次静态持续长度为Lstance,各次摆动持续长度为Lswing,则有:
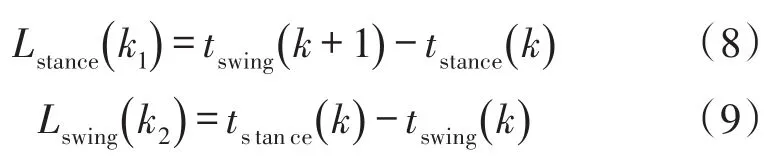
③K均值聚类,将Lstance聚类成真、假静态两类,Lswing聚类成真、假动态两类。
④根据聚类结果选择时间阈值,以静态为例,记真静态最小长度为Lmin,假静态最大长度为lmax,则可按下式选择时间参数(数据长度)阈值:
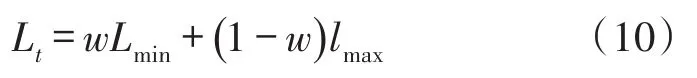
式中0<w<1为根据聚类效果选取的权重,若真静(动)态聚类效果优于假静(动)态,则取w>0.5的值,反之,w<0.5。
图8分别给出基于本文设计方案得到的一组正常行走数据初始检测结果静态和动态的聚类效果。其中,每一数据点代表一次静态或动态。
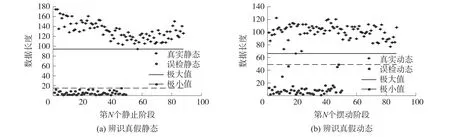
图8 K均值聚类辨识初始检测步态
3 实验结果与分析
为验证论文所提检测算法的可行性,开展一组直线行走实验。综合考虑数据平滑程度并尽可能降低时间延迟对导航精度影响,设定采样率fs=100 Hz,选择窗口参数w=20并计算时间延迟δt=w/2/fs=0.1 s;初始检测加速度滑动方差阈值设定为σGait=0.01m2/s4。通过对图9描述的初始检测步态曲线分析可以看出,由于选择的方差阈值较小,因测量扰动的存在导致部分处于实际静止阶段的信息被误检为短时动态,引起静止阶段呈现短时静态与短时动态交替出现。依托本文设计方案,通过对初始检测步态分别统计静态与动态出现的时刻并对每次持续的时间进行聚类,然后根据自适应时间参数对误检步态进行纠正,得到图9所示的纠正后步态检测结果。经过修正后的结果具有明显的步伐特征。
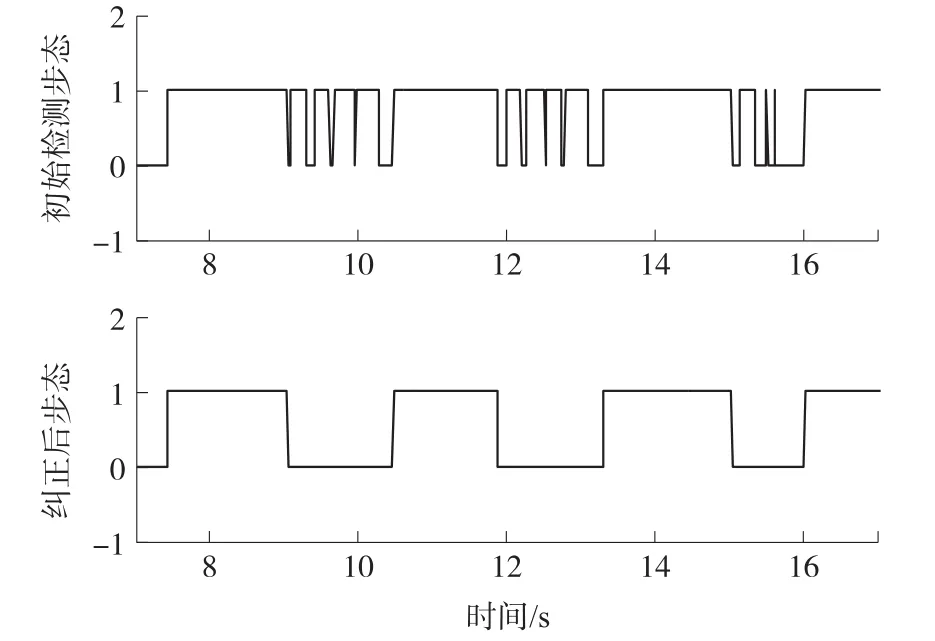
图9 初始检测步态与纠正后步态
将检测步态加经过重力值补偿后与惯性器件输出的加速度幅值进行比对(如图10)。结果表明,尽管足部静止阶段时器件输出存在小范围测量扰动,但是自适应时间参数检测算法仍能准确有效地纠正由于阈值参数选择不当引起的误检步态。
为验证算法可靠性,利用MEMS惯性测量单元分别采集慢速、较慢、常速、较快和快速5种不同行走速度环境下的惯性数据,同时记录真实行走步数。实验场地为测绘学院一楼直线走廊,行走距离70 m为定值,行走步数随行走速度变化而不同。依次对5组数据按提出算法进行步态检测,得到表1所描述的检测结果与真实步数比对值。结果表明在不同行走速度下检测准确率可达到99%以上。

图10 最终步态与加速度幅值
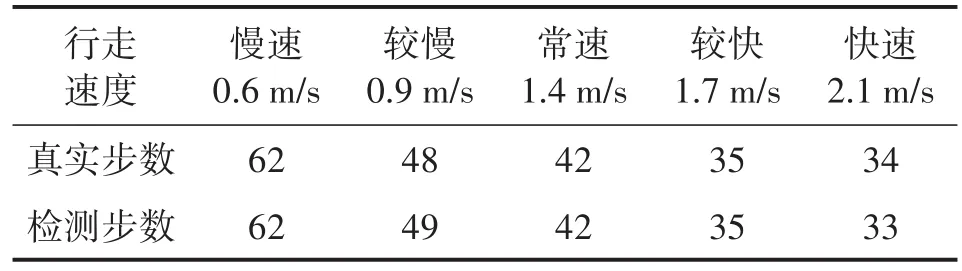
表1 不同行走速度检测结果
4 结论
通过分析人员徒步行走规律,提出采用窗口参数、方差阈值和时间长度3个参数的步态检测算法对行走过程的步态变化进行准确辨识。得出窗口参数和方差阈值用于初始检测步态,时间长度用于纠正初始检测结果的误检步态的结论。其中,窗口大小可由IMU的数据采样率确定,方差阈值仍需根据行走速度确定大致范围,而时间参数通过引入K均值聚类法可自适应确定。为验证算法的可行性,开展多种运动状态下的测试实验,结果表明步伐检测有效率可达到99%,该成果可为人员徒步导航系统的工程化提供技术参考。
[1]张金亮,秦永元,梅春波.基于MEMS惯性技术的鞋式个人导航系统[J].中国惯性技术学报,2011,19(3):253-256.Zhang J L,Qin Y Y,Mei C B.Shoe-Mounted Personal Navigation System Based on MEMS Inertial Technology[J].Journal of Chi⁃nese Inertial Technology,2011,19(03):253-256.
[2]孙伟,李婉秋,初婧,等.基于误差修正技术的井下人员MEMS定位方法[J].传感技术学报,2014,27(7):898-904.Sun W,Li W Q,Chu J,et al.MEMS Position Method for M Based on Error Correction[J].Chinese Journal of Sensors and Actuators,2014,27(7):898-904.
[3]崔潇,秦永元,周琪,等.鞋式个人导航系统算法和试验研究[J].测控技术,2013,32(3):138-142.Cui X,Qin Y Y,Zhou Q,et al.Algorithm and Test Research on Shoe-Mounted Personal Navigation System[J].Measurement& Control Technology,2013,32(3):138-142.
[4]钱伟行,朱欣华,苏岩.基于足部微惯性/地磁测量组件的个人导航方法[J].中国惯性技术学报,2012,20(5):567-572.Qian W X,Zhu X H,Su Y.Personal Navigation Method Based on Foot-Mounted MEMS Inertial/Magnetic Measurement Unit[J].Journal of Chinese Inertial Technology,2012,20(5):567-572.
[5]李超,苏中,朱嘉林.可穿戴式自主定位技术的零速触发算法研究[J].传感技术学报,2014,27(5):627-632.Li C,Su Z,Zhu J L.A Research about Zero Velocity Trigger Algo⁃rithm Used in the Wearable Autonomous Positioning Technology[J].Chinese Journal of Sensors and Actuators,2014,27(5):627-632.
[6]王普,潘凯,任明荣,等.基于伪自适应阈值零速检测法的室内个人导航系统[J].北京工业大学学报,2015,41(9):1308-1313.Wang P,Pan K,Ren M R,et al.Indoor Personal Navigation Sys⁃tem Based on Zero Velocity Detection of Pseudo Adaptive Thresh⁃old[J].Journal of Beijing University of Technology,2015,41(9):1308-1313.
[7]殷红,郭杭,邓晓华.基于Foot-Mounted的IMU室内行人航位推算研究[J].测绘科学,2014,39(1):20-23.Yin H,Guo H,Deng X H.A Research on IMU Indoor Pedestrian Dead Reckoning Based on Foot-Mounted[J].Science of Survey⁃ing and Mapping,2014,39(1):20-23.
[8]Wang Z,Zhao H,Qiu S,et al.Stance Phase Detection for ZUPTAided Foot-Mounted Pedestrian Navigation System[J].Mecha⁃tronics,IEEE/ASME Transactions on,2015,20(6):3170-3181.
[9]Skog I,Nilsson J O,Handel P.Evaluation of Zero-Velocity Detec⁃tors for Foot-Mounted Inertial Navigation Systems[C]//2010 Inter⁃national Conference on Indoor Positioning and Indoor Navigation.Switzerland.2010.
[10]李辰祥.基于MEMS行人惯性导航的零速度修正技术研究[D].厦门:厦门大学,2014.Li C X.Research on Zeero-Velocity Update Technology of Pedes⁃trian Inertial Navigation Based on MEMS[D].Xiamen:Xiamen University,2014.
[11]Skog I,Handel P,Nilsson J O,et al.Zero-Velocity Detection an Algorithm Evaluation[J].Biomedical Engineering,2010,57(11):2657-2666.
[12]万骏炜,曾庆化,陈磊江,等.行人惯性导航系统平台设计与实现[J].计算机应用与软件,2015,32(2):45-47.Wan J W,Zeng Q H,Chen L J,at.al.Design and Implementation of Pedestrian Inertial Navigation System[J].Computer Applica⁃tions and Software,2015,32(2):45-47.
[13]Jonas C,David T,Fredrik G.Probabilistic Stand Still Detection Using Foot Mounted IMU[C]//2010 13th Conference on Informa⁃tion Fusion(FUSION),2010.
[14]Groves P D.Navigation Using Inertial Sensors[Tutorial][J].Aero⁃space and Electronic Systems Magazine,IEEE,2015,30(2):42-69.
[15]Jimenez A R,Seco F,Prieto J C,et al.Indoor Pedestrian Naviga⁃tion Using an INS/EKF Framework for Yaw Drift Reduction and a Foot-Mounted IMU[C]//2010 7th Workshop on Positioning Navi⁃gation and Communication(WPNC),2010.
孙伟(1984-),男,教授,博士生导师,黑龙江萝北县人。2007年于哈尔滨工程大学获得学士学位,2011年于哈尔滨工程大学获得博士学位。长期从事惯性导航技术研究,sunwei-3775235@163.com;

丁伟(1992-),男,四川省巴中市人。现为辽宁工程技术大学测绘与地理科学学院硕士研究生。从事惯性导航与组合导航方法研究。
Research on Adaptive Gait Optimization Detection Method in Pedestrian Navigation System*
SUN Wei*,DING Wei,LI Ruibao
(School of Geomatics,Liaoning Technical University,Fuxin Liaoning 123000,China)
According to that the highly positioning precision of pedestrian navigation system depend heavily on the re⁃liability and accuracy of gait detection,an adaptive gait detection method was proposed,which adjust parameter based on K-means clustering.Foot motion during walking phases was studied firstly,and analyzed the data characteristics of inertial measurement output acceleration and angular velocity,then proposed gait detection scheme which using the amplify of specific force as its detection basis.The three key parameters,the window size of sliding variance,the ini⁃tial detection threshold and the time parameter in false correction and their relationship were also analyzed respective⁃ly,and find out the basic selection rules of the widow parameter and the initial threshold,while the time parameter can be adaptively selected using K-means clustering in order to correct the false detected gait in initial detection result.Five groups walking experiments under different conditions was carried out using laboratory existing MEMS sensors,the experimental results verified the feasibility and effectiveness of the proposed gait detection algorithm.
pedestrian navigation system;gait detection;moving variance;K-means clustering;adaptability

U666.12
A
1004-1699(2016)09-1389-06
项目来源:国家自然科学基金项目(41304032);高等学校博士学科点专项科研基金项目(新教师类)(20132121120005);第8批中国博士后科学基金特别项目(2015T80265);第58批中国博士后科学基金面上项目(2015M581360);辽宁省高等学校杰出青年学者成长计划项目(LJQ2015044);辽宁省“百千万人才工程”培养经费项目(辽百千万立项[2015]76号);辽宁省自然科学基金项目(2015020078);江西省数字国土重点实验室开放研究基金项目(DLLJ201501);精密工程与工业测量国家测绘地理信息局重点实验室开放基金项目(PF2015-13);地球空间环境与大地测量教育部重点实验室开放基金项目(14-01-05);对地观测技术国家测绘地理信息局重点实验室开放基金项目(K201401);海岛(礁)测绘技术国家测绘地理信息局重点实验室项目(2014B05)
2016-02-26修改日期:2016-03-28

