一种基于混杂系统的Boost变换器切换控制算法

方炜，丁辰晨，甘洋洋，刘晓东，刘宿城

（安徽工业大学电力电子与运动控制重点实验室，马鞍山243002）

一种基于混杂系统的Boost变换器切换控制算法

方炜，丁辰晨，甘洋洋，刘晓东，刘宿城

（安徽工业大学电力电子与运动控制重点实验室，马鞍山243002）

Boost变换器既有开关动作上的离散性，又有连续子系统，是典型的混杂动态系统。根据混杂切换理论建立Boost功率变换器的混杂模型，分别讨论变换器在CCM和DCM两种工作模式下的切换控制策略。在固定的系统工作频率下，通过检测电感纹波电流与理论值相比较来控制功率开关器件导通或关断，由此得到所需的占空比信号，从而实现Boost功率变换器的混杂切换的控制。根据电容电荷平衡原理，对负载电流进行估算，减少电路中被检测量，简化控制器的设计并提高了效率。最后，在Matlab/Simulink环境下进行仿真实验，验证了所提控制算法的有效性。

Boost变换器；混杂切换系统；控制算法；电感电流

引言

作为一种基本的电力电子功率开关变换器，Boost型DC/DC升压变换器已广泛地应用在航空、新能源开发、混合动力汽车等领域。利用基于状态空间平均法基础上的小信号建模对其进行分析和控制，是一种近似平均的方法，将非线性的Boost变换器模型线性化处理，并忽略了功率开关器件的离散动作。这种小信号建模方法得到的Boost变换器为非最小相位系统，系统动态响应缓慢，无法满足当前对Boost变换器性能指标的高要求。

近年来，国内外的研究学者在Boost功率变换器的建模以及控制方面做了大量的研究工作。文献［1-3］利用滑模控制设计滑模控制器实现对Boost变换器的控制，改善变换器的动态性能；文献［4-5］通过模型预测控制算法对Boost变换器进行研究，对系统进行优化；文献［6-7］利用模糊控制、文献［8］利用H∞控制、文献［9-11］利用非线性多环控制等方法都有对Boost变换器进行过研究。上述各方法在一定程度上改善了Boost变换器的动态性能，但有的方法仍然依赖小信号模型，或者算法以及控制器的设计较为繁琐，系统的鲁棒性能不佳，或者限于电感电流连续模式CCM（continuous current mode）模式下的控制。文献［12-13］利用混杂控制对Buck-Boost变换器进行建模，讨论CCM和电感电流断续模式DCM（discontinuous current mode）2种模式下的电感电流纹波的控制。

本文根据混杂系统理论对Boost变换器进行建模并控制，检测电感电流值并由此控制功率开关器件的动作，从而实现Boost变换器在CCM以及DCM条件下的混杂状态切换。当负载发生跃变时，利用电容电荷平衡原理，本文对新的负载电流进行估算，进而减少了被检测量，简化了控制器的设计。

1　Boost功率变换器的建模和状态切换

1.1模型建立

Boost变换器是典型的DC/DC升压型变换器，整个系统所呈现出的混杂特性构建模型来描述。图1所示为理想的Boost变换器结构拓扑。

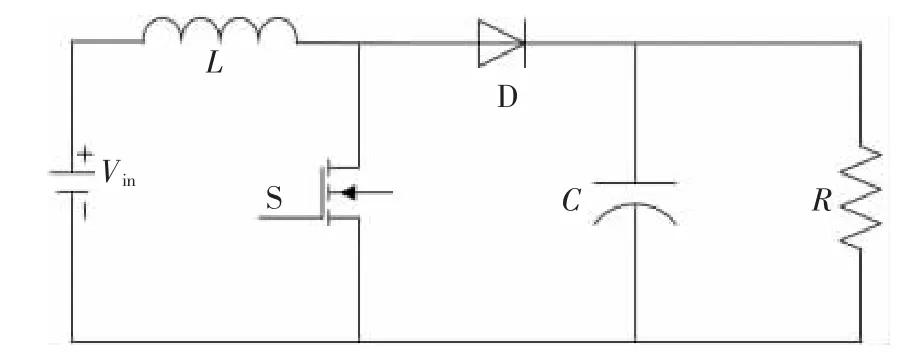
图1　理想Boost变换器结构拓扑Fig.1 Topology of ideal Boost converter structure

（1）CCM模式下系统的工作情况如下：电路分为开关S导通与二极管D交替导通两个阶段。开关S导通、D反向截止时，记工作状态为Q1，即电感L的储能阶段，此时电源Vin不断向电感L提供能量，负载R由存储于电容C中的能量维持工作；当开关S截止、D导通时，记工作状态为Q2，电源和电感同时向负载供电，电容C处于充电阶段。两个线性工作模态可描述为

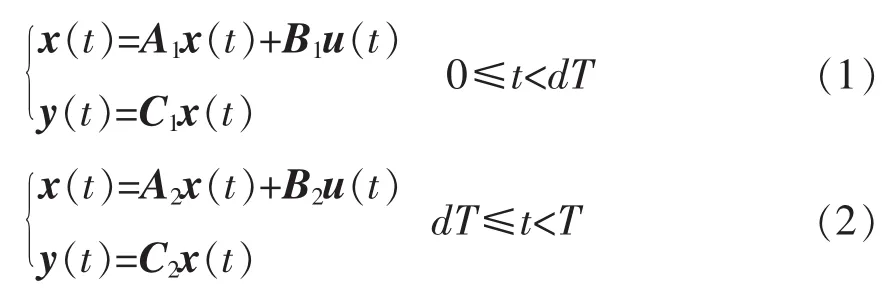
式中：d为开关管导通的占空比，d=ton/T，ton为导通时间，T为开关周期；x（t）=［iL（t）vo（t）］T，x为状态变量，iL为电感电流，vo为输出电压；u（t）=［vin（t）0］T，u为输入变量，vin为输入电压；y为输出状态变量；A1、B1、C1、A2、B2、C2为系统系数矩阵，与电路结构以及参数有关。

（2）当系统工作于DCM模式时，比连续模式多出一种工作状态记为Q3，即开关S和D同时截止，此时电感电流为0，负载由电容提供能量。其工作模态描述为

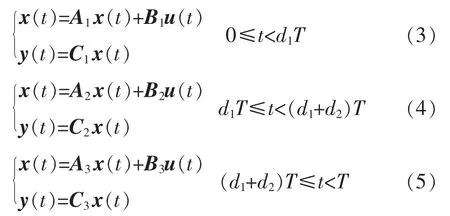
式中：d1为系统工作在Q1状态时的时间；d2为系统工作在Q2状态时的时间；A3、B3、C3为系统工作在Q3状态时系统的矩阵系数。

1.2状态切换

通过上面系统模型的建立，容易得到在整个Boost功率变换器工作过程中，共可能出现3种工作状态：Q1、Q2和Q3，系统要么稳定工作在任何一种状态，要么从一种状态切换到另一种状态。3种状态之间的切换［14］如图2所示。

图2中，当系统稳定工作在Qi（i=1，2，3）时，为连续事件；而当系统从一种状态向另一种状态转换时，为离散事件qij（i=1，2，3；j=1，2，3）。系统工作在Qi（i=1，2，3）时对应的状态方程已经由式（1）～式（5）给出，关键是设计一种控制规则使系统在一定条件下完成从一种状态向另一种状态的转换，即离散事件qij（i=1，2，3；j=1，2，3）的控制律。

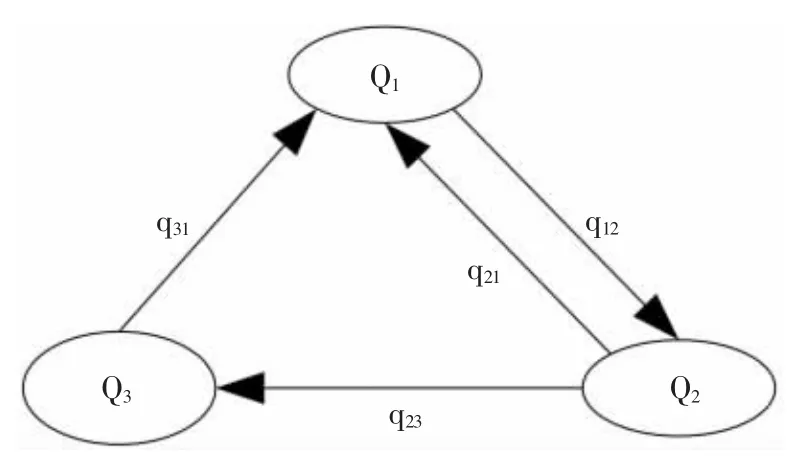
图2　系统工作状态切换Fig.2 State switching of Boost converter

2　控制策略

从图2及以上分析可以看出整个混杂系统中，控制的核心问题即离散事件qij（i=1，2，3；j=1，2，3）的触发选择问题。在CCM条件下，存在2种情况：从Q1向Q2转换的触发事件q12以及从Q2向Q1转换的触发事件q21。而在DCM条件下，存在4种情况：从Q1向Q2转换的触发事件q12、从Q2向Q1转换的触发事件q21、从Q2向Q3转换的触发事件q23以及从Q3向Q1转换的触发事件q31。对于以上所考虑的CCM和DCM两种情况来说，离散事件触发点的计算主要根据本文介绍的控制算法。

2.1CCM模式下的控制策略

如图3所示为理想Boost变换器在CCM模式下电感电流iL和输出电压vo波形。图3中，IP、IL、IV、ΔiL、Vo和ΔVo分别为电感电流的峰值、电感电流平均值、电感电流谷值、电感电流纹波值、输出电压平均值和输出电压纹波值；dT为系统从Q1向Q2转换的时间。

根据图3可知，系统在CCM条件下，可以根据电感电流的峰值及谷值作为判断开关器件的通断条件：当检测到电感电流达到峰值IP时，控制开关S截止，D导通，电感开始放电，系统由Q1向Q2转换；当检测到电感电流放电达到谷值IV时，控制开关S导通，D截止，重新由电源给电感充电，系统由Q2向Q1转换。

通过上面控制策略的分析，可以简单地概括如下：通过检测电感电流iL值，并令其与电感电流的峰值和谷值进行比较，当iL≥IP时，断开开关S；当iL≤IV，闭合开关S。而电感电流平均值IL和电感电流纹波值ΔiL可以根据简单的电路原理计算得出。

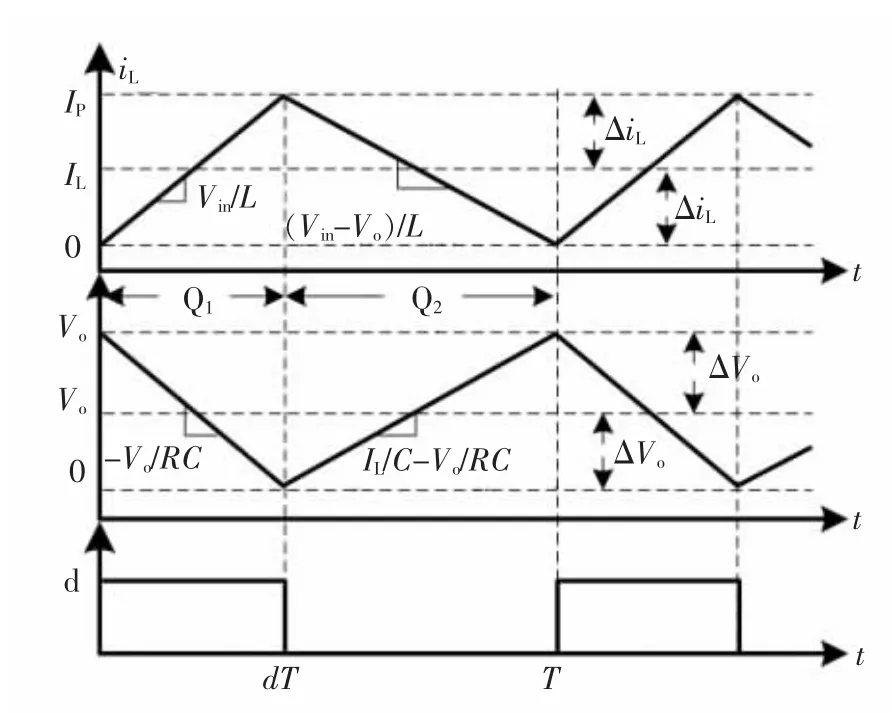
图3　CCM模式下状态变量波形Fig.3 Waveforms of status variables in CCM

从图3可见，在0≤t＜dT时间段电感满足

由于2ΔiL=diL，所以可得

同样的，相同时间段内电容满足

由于2Δvo=-dvo，可得

因此由式（7）和式（9）可得

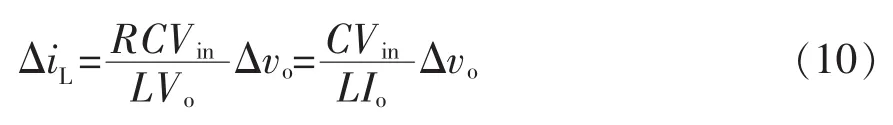
再依据能量守恒，由变换器输入端能量与输出端能量相等可得

最终得到IP=IL+ΔiL，IV=IL-ΔIL。因此根据控制策略即可实现CCM模式下对Boost变换器的控制。

2.2DCM模式下的控制策略

图4所示为系统工作在DCM条件下时状态变量波形。

DCM条件下系统共有3种工作状态：Q1、Q2和Q3，通过在这3种状态之间相互切换实现对占空比的控制，如图4所示，在0＜t≤d1T这段时间内，系统工作在状态Q1；在d1T＜t≤d2T时间段内，系统工作在状态Q2；而在d2T＜t≤T这段时间内，系统工作在状态Q3。DCM比CCM多出一个状态Q3，即开关管S和二极管D同时截止的情况。因此，在控制策略上也要考虑从状态Q2向Q3的切换，以及再从状态Q3向Q1的切换。系统由Q1向Q2状态的切换和CCM条件下的控制策略是一样的，而当检测到电感电流降为0时，D截止（此时S已经处于断开状态），实现由Q2向Q3的切换；进入Q3状态后，负载由电容开始供电，输出电压开始降低，当检测到输出电压降为平均值Vo时，需控制S闭合，电源开始给电感充电，系统完成由状态Q3向Q1的切换［15］。

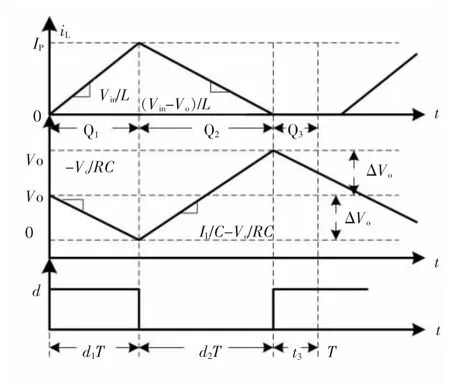
图4　DCM模式下状态变量近似波形Fig.4 The waveforms of status variables in DCM

有必要指出，由Q1向Q2切换条件虽然是通过电感电流iL与电感电流峰值IP进行比较来判断的，但由于DCM条件下电感电流峰值IP不再满足IP= iL+ΔiL，所以前面的控制策略不再适用于DCM。

当系统工作在Q1状态时，有

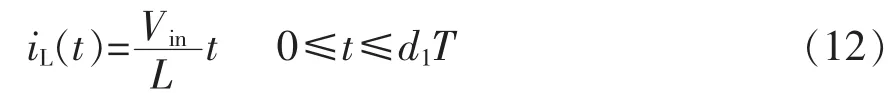
在d1T时刻，有

当系统工作在Q2状态时，电感电流为

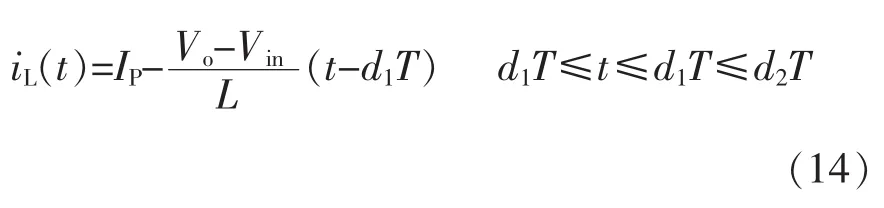
因为在d1T+d2T时刻，电感电流为0，由式（14）可以推出

根据能量守恒定律，则有

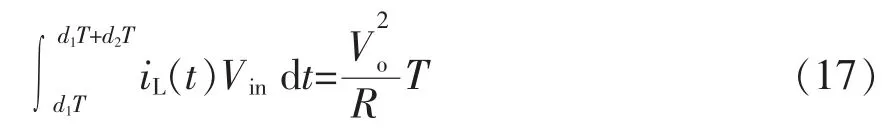
由式（14）、式（15）、式（17）可推出

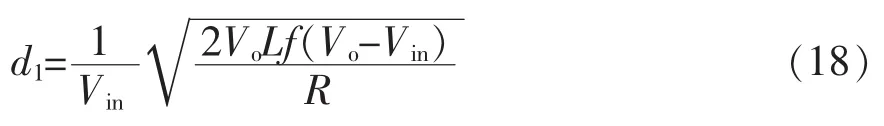
由式（13）、式（15）、式（16）以及式（18）可得

这样得到DCM下电感电流的峰值，根据上面的控制策略可实现对DCM条件下功率开关器件的控制。

另外，由式（19）可以看出，DCM模式下的电感电流峰值IP也与频率f有关，频率越低，峰值越大。峰值不会无限制增大，在保证是DCM模式的前提下对频率将会有一个最小值的限制。根据图4可得限制条件为

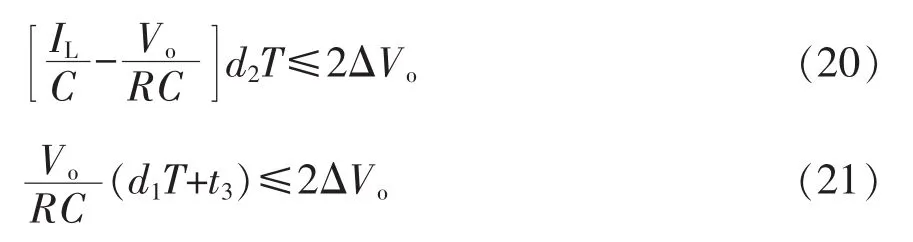
由不等式（20）、（21）可推导出最低频率限制条件为

因此，整个系统所选取的频率f应最低满足式（22）才能保证系统有可能工作于DCM模式。

2.3系统工作模式分析

在整个系统的频率已经选定，即固定频率条件下，影响系统工作模式的因素主要是负载的大小。从CCM到DCM中间有个过渡过程，即CCM条件下电感电流的谷值恰好为0。此时，CCM条件下的功率开关器件导通时间应与DCM条件下的功率开关器件的导通时间相等，即图3中的dT与图4中的d1T值相等。这样可以得出临界条件下的负载为

因此，当电阻R值小于RC时，系统将工作于CCM模式；当电阻R值等于RC时，系统介于CCM到DCM的临界工作点处；当电阻R值大于RC时，系统将工作于DCM模式。

3　负载跳变时输出电流的估算

通过前面计算可知，控制律与负载有着密切关系。实际电路中，系统工作环境复杂，突发状况也很多，负载电流发生未知跳变这种情况也时常发生。而负载发生跃变会引起输出电流进而引起电感电流和输出电压的变化，整个系统将不再稳定工作。因此必须根据新的负载对Boost变换器的切换条件进行调整控制，才能保证Boost变换器的正常工作。本文利用估算电流法改进对Boost变换器的混杂切换控制。

针对负载发生跃变的情况，分负载正跃变和负载负跃变两种情况分析。负载跃度瞬态工作过程如图5所示。

3.1负载负跃变

当负载发生负跃变，电感上的电流应开始调整变小开始放电［16］。图5（a）中，在极短时间内，负载上电流立即减少，只能回馈到电容上，电容上的电荷量也会发生变化。在这段过程中，跳变之后新的输出电流i'o应满足

实际工作过程中，负载发生跃变时状态变量的调整是非线性的，这里为了便于分析并考虑到调整过程很短而将其理想化。负载负跃变暂态过程中状态变量波形示意如图6所示，在电容电压急剧下降过程中选取一个调整时间Tc（Tc应小于一个工作周期），通过采样得到Tc前后的两组状态变量的值分别为iL1、iL2、vo1和vo2。这时，电感电流和电容电压应满足

由式（24）～式（26）可得出负载发生负跃变时输出电流的估算公式，即

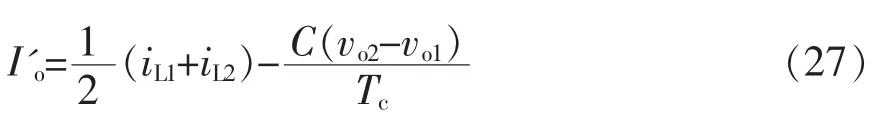
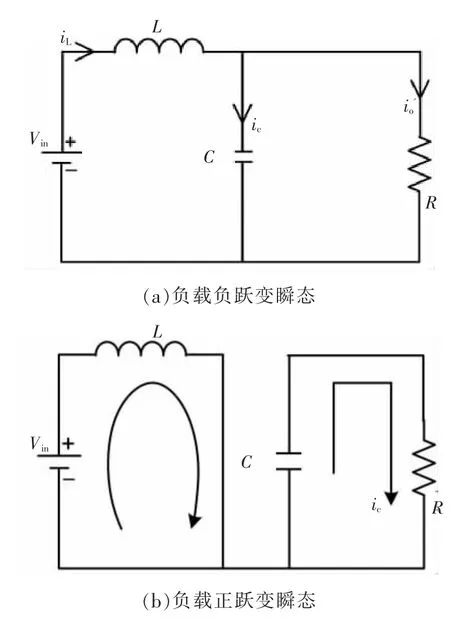
图5　负载跃变瞬态工作过程Fig.5 Working process after load changed

图6　负载负跃变暂态过程中状态变量波形示意Fig.6 Waveforms of status variables when the load increases

3.2负载正跃变

当负载发生正跃变时，负载电流瞬间变大，电感需立即进行充电以及时补充负载所需的额外电流。但在极短时间内，电感电流需要先充电，如图5（b）所示，电感充电，在调整瞬间负载电流由电容上的电荷进行迅速地补充。因此，在这一暂态过程中，负载电流应等于电容电流。即跳变后的输出电流I'o满足

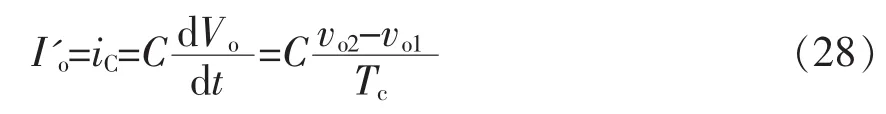
通过上面分析可以看出，在负载发生跃变后的输出电流可以通过检测采样调整过程中的两个时间点处的电感电流和输出电压（或只检测两个输出电压量）的值来估算。

负载正跃变或负跃变各自估算出的输出电流值代入不同模式下电感电流的峰值和谷值公式中，便可得到跳变后理论上新的电感电流峰值以及谷值。再按照新的理论值对系统进行控制。

式中的I'P为负载跳变后的电感电流峰值；I'V为跳变后的电感电流谷值。

通过这种估算法，只需检测Boost变换器的输出电压和电感电流，因此控制器的设计更为简单。

4　Simulink仿真和仿真结果分析

为了验证控制方案及算法改进的有效性，通过Matlab/Simulink予以验证。其中，Boost变换器的主电路参数为：输入电压Vin=3.7 V，输出电压Vo=5 V，Δvo=1%Vo，L=10 μH，C=200 μF，开关频率固定在f=100 kHz，开关周期T=10 μs。要求负载从3 A跳变到6 A（正跃变）和从6 A跳变到3 A（负跃变）。鉴于CCM和DCM条件下控制策略是一样的，仅是系统状态及状态切换条件有所不同。因此，本文通过Simulink环境里CCM条件下的仿真实验去验证控制方案的可行性。

图7为CCM条件下负载发生正跃变时利用估算法得出的系统状态变量波形。

图7中，由于正跃变时负载从3 A正跃变至6 A，从0.005 s开始，根据跳变利用估算法得到的输出电流的估算结果约为5.72 A，iL为电感电流的波形，vo为输出电压的波形。可以看出，由于固定频率下负载增加了1倍，输出电压纹波值增加了1倍；其次，在误差允许范围内输出电压经过大概170 μs的调整时间最后稳定在5 V左右。

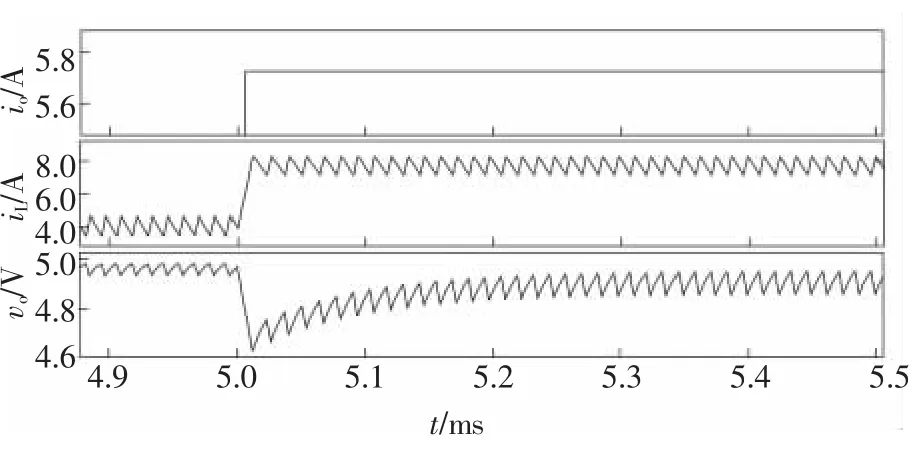
图7　CCM条件下负载发生正跃变时系统状态的波形Fig.7 Waveforms of status variables when the load decreases in CCM

图8所示为负载负跃变从6 A跳变到3 A时的系统状态波形图。图8中，从0.05 s开始，负载发生负跃变，根据跃变过程利用估算法得出的输出电流约为2.92 A，中间波形为电感电流负跃变前后的波形，第三个波形为输出电压在负载发生负跃变前后的波形。由图可以看出，输出电压的纹波不仅随着负载减小而减小了并且经过大概400 μs的调整时间最终稳定在5 V左右。

从仿真结果可看出，本文所提的控制算法，能够较为准确地计算出负载电流，实现Boost变换器的混杂切换控制。

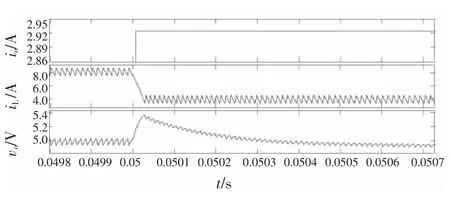
图8　CCM条件下负载发生负跃变时系统状态的波形Fig.8 The waveforms of status variables when the load increases in CCM

5　结语

传统的小信号建模方法针对Boost变换器的建模及控制是一种基于线性化平均的近似处理，无法精确地反映实际中Boost变换器的非线性动力学特征，且当负载发生跳变时，系统很容易不稳定。本文通过混杂控制的方法，根据新的控制算法实现对占空比的控制，即使当负载发生跃变，仍然能很好地对系统进行调节控制，保证了系统的稳定性。不仅如此，这种控制算法同时适用于CCM和DCM两种工作情况，弥补了以往大多算法只适用于CCM工作情况的欠缺。同时，通过对输出电流的估算实现控制算法的改进，减少了高频信号的检测，简化控制器的设计。为了证明新算法和估算的可行性，通过仿真实验在原理上对其进行了验证，实现了Boost变换器在混杂控制算法下的稳定运行。

［1］乐江源，谢运祥，洪庆组，等.Boost变换器精确反馈线性化滑模变结构控制［J］.中国电机工程学报，2011，31（30）：16-22. Le Jiangyuan，Xie Yunxiang，Hong Qingzu，et al.Sliding mode control of boost converter based on exact feedback linearization［J］.Proceeding of the CSEE，2011，31（30）：16-22（in Chinese）.

［2］屈鲁.Buck-Boost变换器的无源滑模控制研究［J］.电源学报，2013，11（2）：105-109. Qu Lu.Analysis on the passively and sliding mode control of the Buck-Boost converter［J］.Journal of Power Supply，2013，11（2）：105-109（in Chinese）.

［3］Hussainy S A A，Tandon R G，Kumar S.PWM based sliding mode control of DC-DC converters［C］.Advances in Power Conversion and Energy Technologies（APCET），Mylavaram，Andhra Pradesh：IEEE，2012：1-6.

［4］张聚，丁靖.DC-DC变换器显示模型预测控制［J］.吉林大学学报：工学版，2011，41（1）：270-274. Zhang Ju，Ding Jing.Explicit model predictive control of DC-DC converters［J］.Journal of Jilin University：Engineering and Technology Edition，2011，41（1）：270-274（in Chinese）.

［5］Rodriguez J.Model predictive controller of boost converter with RLE load［J］.International Journal of Computer Applications，2010，11（3）：13-17.

［6］Ismail A，Omer F B.A type-2 fuzzy logic controller design for buck and boost DC-DC converters［J］.Journal of Intelligent Manufacturing，2012，23（4）：1023-1034.

［7］Guo Liping，John Y H，Nelms R M.Design of a fuzzy controller using variable structure approach for application to DC-DC converters［J］.Electronic Power Systems Research，2011，83（1）：104-109.

［8］冉华军，张涛.随机PWM CCM Boost变换器非脆弱H∞控制［J］.福州大学学报：自然科学报，2013，41（2）：202-206. Ran Huajun，Zhang tao.Non-fragile H∞control for random PWM CCM Boost converter［J］.Journal of Fuzhou U-niversity：Natrual Science Edition，2013，41（2）：202-206（in Chinese）.

［9］郑会军.Buck-Boost变换器非线性电流控制研究［J］.电力电子技术，2012，46（10）：106-109.Zheng Huijun.A novel nonlinear current control method for Buck-Boost converter［J］.Power Electronics，2012，46（10）：106-109（in Chinese）.

［10］Wang Zheng，Zhu Xingdong.The nonlinear control for the DC-DC boost switched-mode power converter［C］.Electrical and Control Engineering（ICECE），Wuhan：IEEE，2010：2379-2382.

［11］梁永春，许丽川，严仰光.一种双闭环控制隔离Boost变换器启动控制策略［J］.中国电机工程学报，2010，30（24）：15-20. Liang Yongchun，Xu Lichuan，Yan Yangguang.New startup schemes for isolated boost converter in double closeloop control［J］.Proceeding of the CSEE，2010，30（24）：15-20（in Chinese）.

［12］Ma Hongbo，Feng Quanyuan.Hybrid modeling and control for Buck-Boost switching converters［C］.Proceedings of IEEE Conference on Circuits and Systems，California：IEEE，2009：678-682.

［13］Quan Yu，Wang Xuemei，Zhang Bo.A study of hybrid control algorithms for buck-boost converter based on fixed switching frequency［C］.Industrial Electronics and Appli-cations（ICIEA），Melbourne：IEEE，2013：1197-1202.

［14］Sreekumar C，Agarwal V.A hybrid control algorithm for voltage regulation in DC-DC Boost converter［J］.IEEE Trans on Industrial Electronics，2008，13（3）：971-978.

［15］Gupta P，Patra A.Hybrid mode switched control of DCDC boost converter circuits［J］.IEEE Transactions on Circuits Systems，2007，54（5）：2688-2696.

［16］刘虎，邱亚杰，刘晓东，等.电容充放电平衡控制Buck变换器动态响应特性分析［J］.电机与控制学报，2010，14（6）：77-82.Liu Hu，Qiu Yajie，Liu Xiaodong，et al.A control algorithm based on capacitor charge balance during transient for Buck converter［J］.Electronic Machines and Control，2010，14（6）：77-82（in Chinese）.

A Switching Control Algorithm of Boost Converter Based on Hybrid System

FANG Wei，DING Chenchen，GAN Yangyang，LIU Xiaodong，LIU Sucheng
（Key Lab of Power Electronics and Motion Control，Anhui University of Technology，Ma'anshan 243002，China）

Boost converter is a typical hybrid dynamic system including both discrete and continuous subsystems. Based on hybrid switching control theory，the hybrid model of Boost converter was built.And then this paper discussed the switching control strategies of the converters working in continuous current mode（CCM）and DCM modes.On condition that the switching frequency was fixed，the duty cycle was obtained by comparing the inductor current with its theoretical value，which achieved the hybrid switching control of the Boost DC-DC converter.Meanwhile，according to the principle of capacitor charge balance，the load current was estimated instead of by detection which simplified the design and improved the efficiency.Finally，the simulation results show that the proposed algorithms are effective.

Boost converter；hybrid switching system；control algorithm；inductor current

方炜

10.13234/j.issn.2095-2805.2016.5.60

TM 461

A

方炜（1977-），男，博士，副教授，研究方向：电力电子功率变换技术以及非线性控制，E-mail：fwei2k@163.com。

丁辰晨（1992-），女，通信作者，硕士研究生，研究方向：电力电子功率变换技术，E-mail：agd511cc@163.com。

甘洋洋（1993-），男，硕士研究生，研究方向：电力电子功率变换技术，E-mail：ahutgydx1375764525@163.com。

刘晓东（1971-），男，博士，教授，研究方向：电力电子功率变换技术，E-mail：lxdong168@sina.com。

刘宿城（1981-），男，博士，研究方向：电力电子系统稳定性分析与控制，E-mail：liusucheng@gmail.com。

2015-11-25

国家自然科学基金资助项目（51207001）；安徽省自然科学基金资助项目（1308085ME66）

Project Supported by the National Natural Science Foundation of China（51207001）；Anhui Provincial Natural Science Foundation（1308085ME66）