快递末端物流配送仿真优化研究
李乃文,赵云龙,李 丹
(辽宁工程技术大学,辽宁 葫芦岛 125105)
快递末端物流配送仿真优化研究
李乃文,赵云龙,李 丹
(辽宁工程技术大学,辽宁 葫芦岛 125105)
为了满足减少城市“最后一公里”物流配送费用的要求,在城市配送的“最后一公里”建立配送中心并整合所有物流公司,实现协同配送,以物流配送费用最小为原则构建模型,提出模型假设和约束条件,列出目标模型并用MATLAB软件求解出最优配送中心并优化配送路径。
协同配送;“最后一公里”;配送中心;仿真优化
1 城市“最后一公里”物流配送的现状
我国现在知名的快递公司有顺丰、天天、中通、圆通、申通和韵达等,这些快递公司在城市“最后一公里”配送阶段几乎都是自行配送,这就造成了物流配送车辆在配送快递时,出现车辆不满载甚至半空车的现象,并且由于配送路线规划的不合理,延长了车辆配送的配送距离。这些现象不仅严重地增加了配送的成本和配送需要的时间,同时,大量的快递车辆排放的尾气也增加了城市环境保护的负担。
由于我国在城市“最后一公里”物流配送的情况不是很理想,各种问题层出不穷,特别是在双11之类的节假日显得格外突出。因此,本文旨在解决有限区间内进行协同配送的问题,
主要步骤如下。
①在城市配送的物流末端的上一层建立配送中心;②根据末端节点的快递业务需求量,来确定在物流配送的末端节点的配送范围,并在这个范围中找个合适的位置作为协同配送的末端节点。③确定配送中心到各个末端节点的距离。
根据每天各个快递公司到配送中心的快递数量并对其按各个末端节点的需求进行分类,用MATLAB软件仿真优化技术对该配送中心内待配送货物进行统筹和整合,从而实现配送中心到末端节点的统一配送。一方面,进行统一安排配送的时间、车辆、次数、路线和货物数量,不仅大大降低了传统的各自配送模式的成本,而且实现了人员、物资等资源的有效利用。
2 快递末端物流配送仿真优化研究假设
①城市“最后一公里”物流配送都使用公路运输,物流公司到配送中心,由配送中心到末端节点的单位公里运输价格均相同。②除了“双十一”等节假日,其他时间的各个末端节点和各个物流公司配送到城市的快递总容积按照平均值计算。③在每一个城市建造配送中心和日常管理费用均为常数,且费用相等。④各个末端节点的位置是按照各个物流公司在某一范围内所设置的站点,将这些站点通过聚类的方法来确定。⑤配送中心的建设费用用10年来进行分摊。
3 仿真模型的构建
选择最优的物流配送中心,使从物流公司在兴城市配送的起点到配送中心,配送中心到末端节点以及配送中心的固定投资费用之和最小。因此,本文主要是以最低的配送成本为目标函数来建立数学模型,建立模型如下。
I:物流公司,I={1,2,…,i};
J:预建配送中心的备选地,J={1,2,…,j};
K:末端节点,K={1,2,…,m,…,n,…,k};
Ai:物流公司配送的快递容量,Ai={a1,a2,…,ai};
Cj:每天分摊的配送中心建设费用,其中Cj1表示土地费用,Cj2表示建筑成本,Cj3表示设施设备成本(单位:公里);
Dij:物流公司i到配送中心j的距离(单位:公里);
Djk:备选配送中心j到末端节点k的距离(单位:公里);
Dmn:表示两个末端节点之间的距离(单位:公里);
Xij:供应商i向备选配送中心j的供货量(供货的货物体积,单位:立方米);
Xjk:备选配送中心j向需求地k的送货量(送货的货物体积,单位:立方米);
Xk:表示货车从末端节点k运送到下一站的载货量(单位:立方米);
Yk:表示末端节点k的需要的送货量;
Z:需要同时派送的车辆数量,Z=5;
Q:表示配送车辆的容量,Q=25(配送车辆都是统一标准);
Ljkz:表示车辆z从配送中心j行驶到末端节点k建立0-1变量;
Lmnz:表示车辆z从末端节点m行驶到末端节点n建立0-1变量;
Smz:表示末端节点m的供货由车辆z在来满足建立0-1变量;
P:表示每立方米货物每公里所需的费用,单位:元/(立方米·公里)。
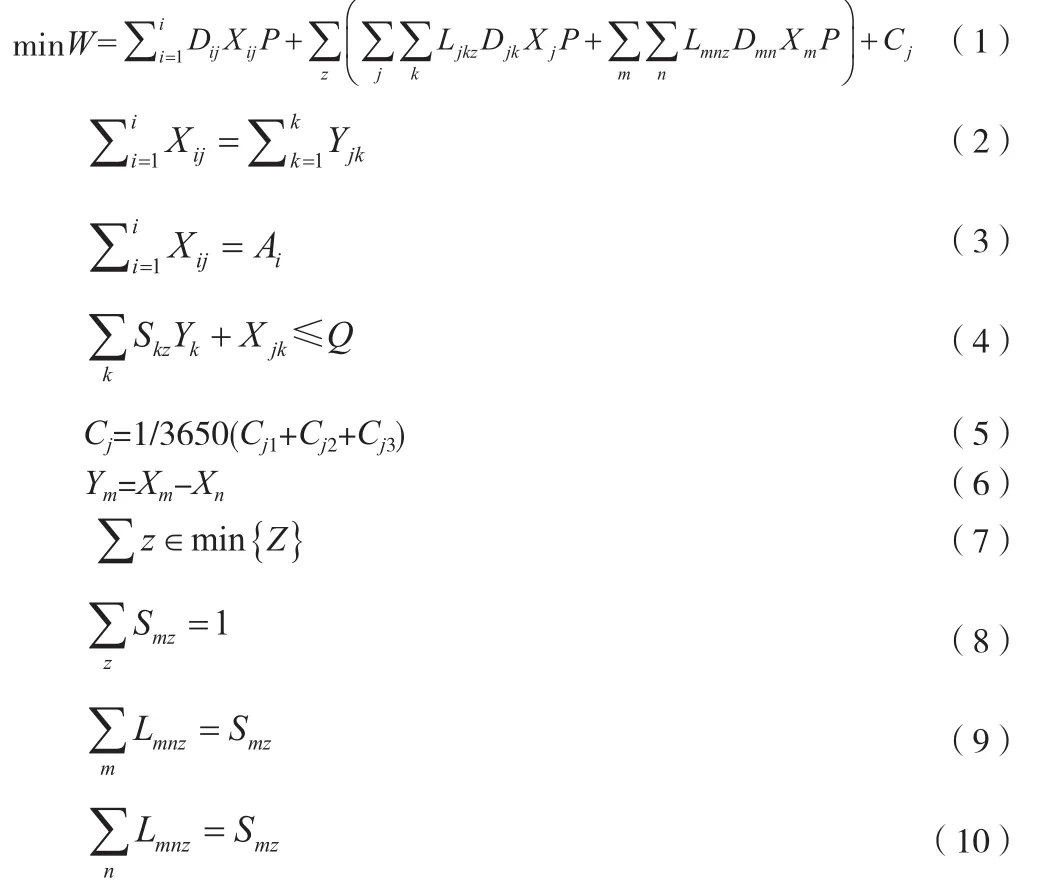

式(1)表示每天进行协同配送所需要花费的费用总和;
式(2)表示每天配送中心到达的快递全部都能配送出去;
式(3)表示各个物流公司的快递全部都要运到配送中心;
式(4)保证每条配送路径各个末端节点的供货总量不超过配送车辆能够容纳的最大量;
式(5)表示每天分摊的配送中心建设费用;
式(6)表示末端节点m向末端节点n的送货量有货车离开末端节点m的载货量与货车离开末端节点n的载货量之差得到的;
式(7)保证配送车辆的数量不超过配送车辆的总量;
式(8)每个末端节点的供货只能有一辆车满足;
式(9)和式(10)表示配送车辆从配送中心出发最后回到配送中心;
式(11)、(12)、(13)表示0-1变量。
4 基于兴城市物流配送的实例分析
4.1基于兴城市物流配送的实例仿真分析
4.1.1兴城市配送中心情况概况
目前,兴城市已知快递公司有顺丰、天天、中通、圆通、申通与韵达等,这些快递公司在兴城“最后一公里”配送阶段都是自行配送,这就造成了物流配送车辆在配送快递时,出现车辆不满载甚至半空车的现象,并且由于配送路线规划的不合理,更加延长了车辆配送的配送距离,这些现象不仅严重的增加了配送的成本和配送需要的时间。
4.1.2相关数据来源
已知建设配送中心的3个备选地到分布在兴城市的20个末端节点的距离(末端节点的选取是在走访兴城市各个快递公司末端节点的情况下,将各个快递公司在一起的末端节点运用聚类的方法确定的)具体数据见表1的Dmn;不同末端节点每天的快递量(快递的总体积,单位用立方米表示)见表2的Hk(k=1,2,…,20);已知配送起点(刚进入兴城市的起点,有以下三个起点:兴城火车点、葫芦岛、兴城汽车站)到备选地的距离具体数据见表3的Dij,而优化前不同快递公司到各个末端节点的每天供货量用Hik(i=1,2,…,6;k=1,2, …,20).因 此,,即Hk=Xjk,Hi=Xij。每天分摊的配送中心建设费用,其中Cj1表示土地费用,Cj2表示建筑成本,Cj3表示设施设备成本(单位:元/天),见表4。同时,物流3从兴城火车站方向运送到配送中心,物流2、4从兴城汽车站方向运送到配送中心,物流1、5、6从葫芦岛方向运送到配送中心。根据本文研究的20个末端节点中,编号1-3也表示3个备选配送中心,编号1-20表示20个末端节点。
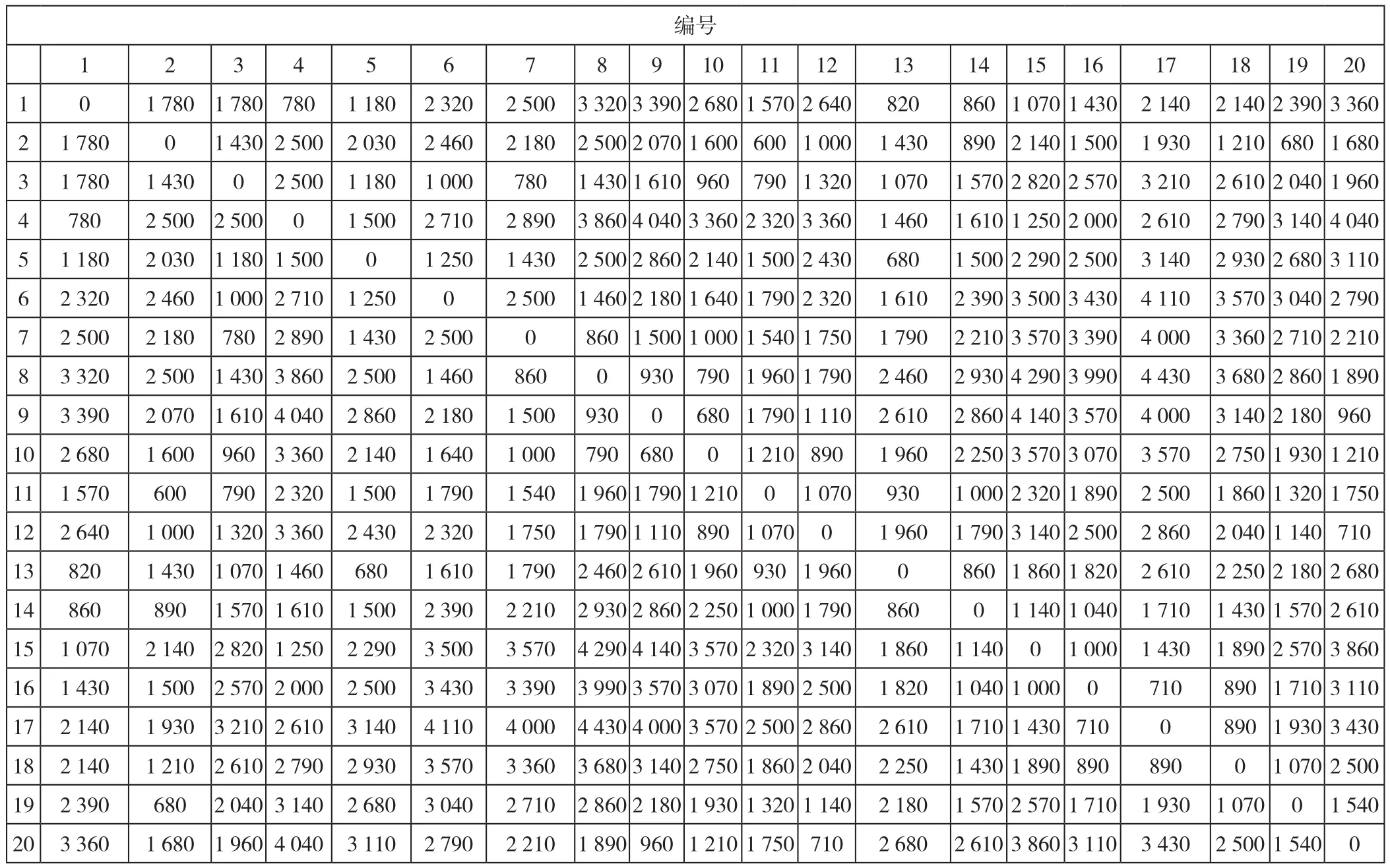
表1 末端节点距离Dmn

表2 配送起点到各个末端节点的配送量
4.1.3求解程序的编写
(1)输入配送中心到各个末端节点的距离Djk(序号1-3其中一个是配送中心但同时都是末端节点)。
(2)将任意两个末端节点连接在一起,利用Smk=Djm+Djk-Dmk,计算节约值,得S={s(m,k)|s(m,k)>0},令j=1,如果有h个末端节点,那么节约值得数量为。
(3)对集合S中的数进行从小到大的排序。
(4)若S是空集,则算法结束.否则,看S是否满足以下任何一个条件,如果满足任何一个则转步骤(5),否则转步骤(7)。
①末端节点m和k都在已经构成的不同线路上,并且分别在各自的首位和末位;②末端节点m和k一个在构成线路上且在首位或者末位,而另一个不在已经构成的线路上;③末端节点m和k都不在已经构成的线路上。
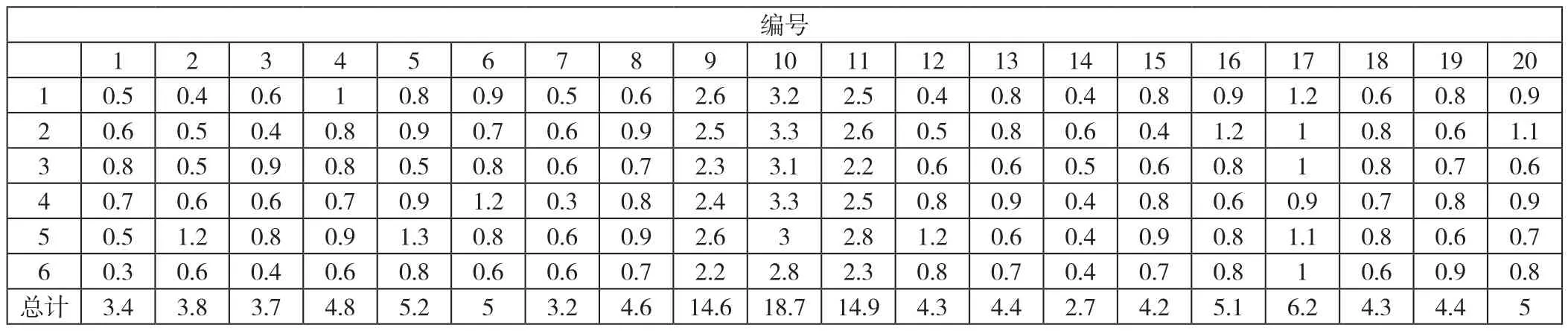
表3 配送起点末端节点的距离Dij
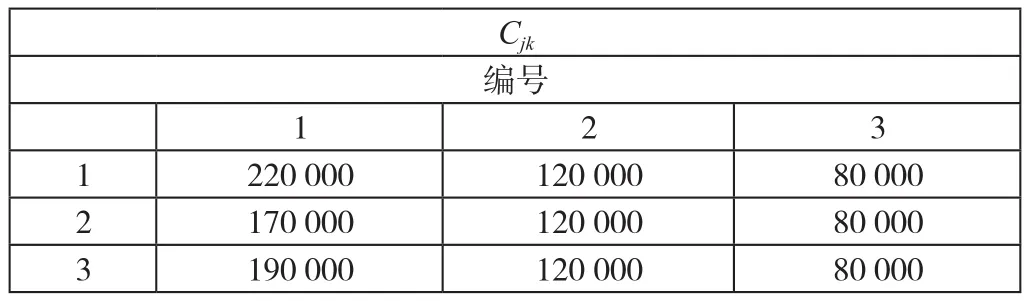
表4 各个部分建设费用
(5)计算连接末端节点m和k之后,线路上的货物量如果小于货车容量则转为步骤(6),否则转步骤(7)。
(6)将末端节点m和k连接成一条配送线路。
(7)删除集合S中的元素,且末端节点m和k不能作为车辆最初或者最终的线路点。接着搜索其余各点,将全部的Ch2各节约值访问完毕。最终,找到一条最优的路线。
(8)再令j=2,令j=3分别找出一条最优路线,然后分别计算所需要花费的费用。
4.1.4实例仿真程序运行结果
当j=1也就是在南关附近建立配送中心,则运行结果为MinW≈1 013(元/天)。
当j=2也就是在北川桥附近建立配送中心,则运行结果为MinW≈1 066(元/天)。
当j=3也就是在金天屹时代广场附近建立配送中心,则运行结果为MinW≈1 044(元/天)。
4.2分析结果
由4.1的分析结果可知,在兴城市南关附近建立配送中心时,每天所需要的运输费用等总和最小而且交通便利,其路径如下。
车辆1:1—11—12—20—1;
车辆2:1—9—8—7—1;
车辆3:1—10—6—1;
车辆4:1—4—15—14—3—5—13—1;
车辆5:1—16—17—18—19—2—1;
运行结果图1所示。

图1 兴城市配送路线图
5 兴城市物流配送优化前后比较
5.1优化前物流配送费用
根据优化前的6家物流公司配送情况来计算物流配送费用,见
4.1.2的具体数据可知,每个物流公司在兴城配送的总数量只需要一辆汽车就可以配送到位,由于优化后末端节点的选择是按照各个物流公司在某一范围内所设置的站点,将这些站点通过聚类的方法确定。所以在这里就近似作为优化前的末端节点进行处理,同时,由于一辆车就可以配送全部站点,因此,这里只需要确定各个物流公司在兴城配送的配送路径然后计算出费用就行,令费用用f表示。
有公式:


跟踪各个公司物流车辆同时也咨询各个物流公司,得到各个物流公司的配送路线如下(末端节点用序号表示)。
物流公司1:火车站—15—14—11—10—9—20—12—2—19—18—16—17—1—13—3—8—7—6—5—4
物流公司2:汽车站—16—14—11—10—9—8—7—6—5—4—1—13—3—20—12—2—19—18—17—16
物流公司3:汽车站—15—16—17—18—19—2—11—10—12—20—9—8—7—3—6—5—13—14—1—4
物流公司4:葫芦岛方向—5—6—7—8—9—20—12—10—3—11—13—4—1—14—2—19—18—17—16—15
物流公司5:葫芦岛方向—6—7—8—9—10—3—5—13—11—12—20—19—2—14—1—4—15—16—18—17
物流公司6:葫芦岛方向—5—6—7—8—9—10—3—11—12—20—19—2—14—13—1—4—15—16—18—17
计算费用如下。

5.2优化前后对比分析
通过优化前和优化后进行对比,可知,优化后各个公司每天的运输费用明显降低,同时,缩短了每辆车的总公里数,来节约配送时间,从而提高了物流配送的经济效益。
主要参考文献
[1]李昌兵,杜茂康,曹慧英.基于层次遗传算法的物流配送中心选址策略[J].计算机应用研究,2012(1).
10.3969/j.issn.1673 - 0194.2016.18.049
F252
A
1673-0194(2016)18-0075-03
2016-08-20

