季节性多元回归模型与时间序列分解模型在内陆用箱需求预测中的应用比较
王腾龙
“一带一路”战略的部署和实施推动我国产业结构调整和经济转型发展,作为连接丝绸之路经济带与海上丝绸之路的桥梁,我国中西部经济走廊的作用和地位越发显现。一方面,随着沿海制造业向内陆转移,腹地货源得到释放,从而带动物流运输业发展;另一方面,在世界经济下行以及集装箱船舶运力严重过剩的背景下,船公司为填满舱位,争相通过向内陆延伸海运服务来扩大营销网络覆盖面,以期从源头上掌握集装箱货源,从而提升直接客户的比例。在内陆存放集装箱无疑有利于保障客户装箱发运的时效性,提升用户体验满意度和客户黏性;但从经营角度而言,船公司必然要面对如何控制内陆用箱这一现实问题。鉴于内陆出货有明显的季节性特点,且内陆调箱存在空间和时间上的局限性,为保障内陆延伸业务稳步开展,船公司需要考虑内陆集装箱存量问题。本文以内陆进出口箱量的历史数据为例,分别采用季节性多元回归模型和时间序列分解模型预测内陆用箱需求,结果表明,时间序列分解模型的预测值更贴近实际观测值;因此,采用时间序列分解模型预测进出口箱量,可得出下一阶段用箱缺口的理论值,从而为船公司主动干预内陆用箱提供量化参考依据。
1 问题描述
在内陆多箱与缺箱之间寻求平衡是船公司业务开拓与成本控制之间的博弈。[1]在实际操作过程中,一方面,为满足客户用箱需求,保证集装箱货物顺利出口,空箱供给需要在特定时间内完成,否则就会产生违约损失和信誉损失,导致船公司丢失市场份额;[2]另一方面,如果过早地预备空箱或管理失控,则会造成空箱积压,而内陆压箱的解决方案非常有限,一般只能等待出货用箱,倘若正值市场淡季,往往会产生高昂的空箱堆存费和调运费。由此可见,适度的内陆存箱规模有助于船公司减少空箱闲置和盲目流动。
内陆用箱供给效率在一定程度上影响着内陆存箱规模。[3]内陆用箱供给主要有以下两种方式:一种是从口岸调运空箱的“空进重出”方式,由于内陆距口岸箱源地路途遥远,组织空箱调运的手续烦琐且费用高昂,难以形成对内陆用箱需求的快速反应和成本优势,故这种方式很难产生规模效应;另一种是进口重箱在内陆拆空还箱后用于出口的“重进重出”方式,这种方式能够避免产生口岸调空费、返空费等费用,对内陆用箱而言更具操作性,但受市场季节性波动等因素的影响,内陆进出口箱量、箱型普遍存在较大差异,容易形成被动用箱供给局面,即在缺少预控标准和量化方法的情况下,内陆存箱量不合理,从而产生压箱或缺箱等负面效果。
将内陆用箱量与存箱量挂钩并强化预控,有助于提高内陆用箱供给效率。根据精益管理理论中的看板拉动原理,在一段时期内,内陆可接受的进口箱量取决于内陆出口箱量;因此,改变被动用箱供给局面的前提是以合理的方法确定内陆用箱量的变化规律,从而确定合理的存箱量,当内陆空箱盘存量与在途进箱量之和偏离合理的存箱量时发出预警,以便船公司及时采取相应措施主动干预,力求将存箱量控制在合理的范围内。
对内陆进出口箱量的历史数据进行分析,发现内陆进出口箱量的季节性特征较为明显,淡季与旺季的用箱需求存在较大差异。这主要是因为地区间货源结构不同,例如,进口货物主要是资源类矿产品,而出口货物主要是农副加工品,容易导致进出口货量形成季节性波动,造成进出口箱量不平衡。根据内陆出货量的时间序列对其进行季节性预测,能够为合理控制内陆存箱规模提供量化依据。
2 季节性多元回归模型在内陆出货量预测中的应用
对于季节性的时间序列,通常采用季节性多元回归模型进行预测。把季节看作分类变量,用于对数据观察值进行分类。当分类变量有n个水平时,通常需要(nHa1)个虚拟变量,因此,4个季度需要3个虚拟变量。[4]对3个虚拟变量进行编码,可以得到:Q1=1(第1季度)或Q1=0(其他季度);Q2=1(第2季度)或Q2=0(其他季度);Q3=1(第3季度)或Q3=0(其他季度)。
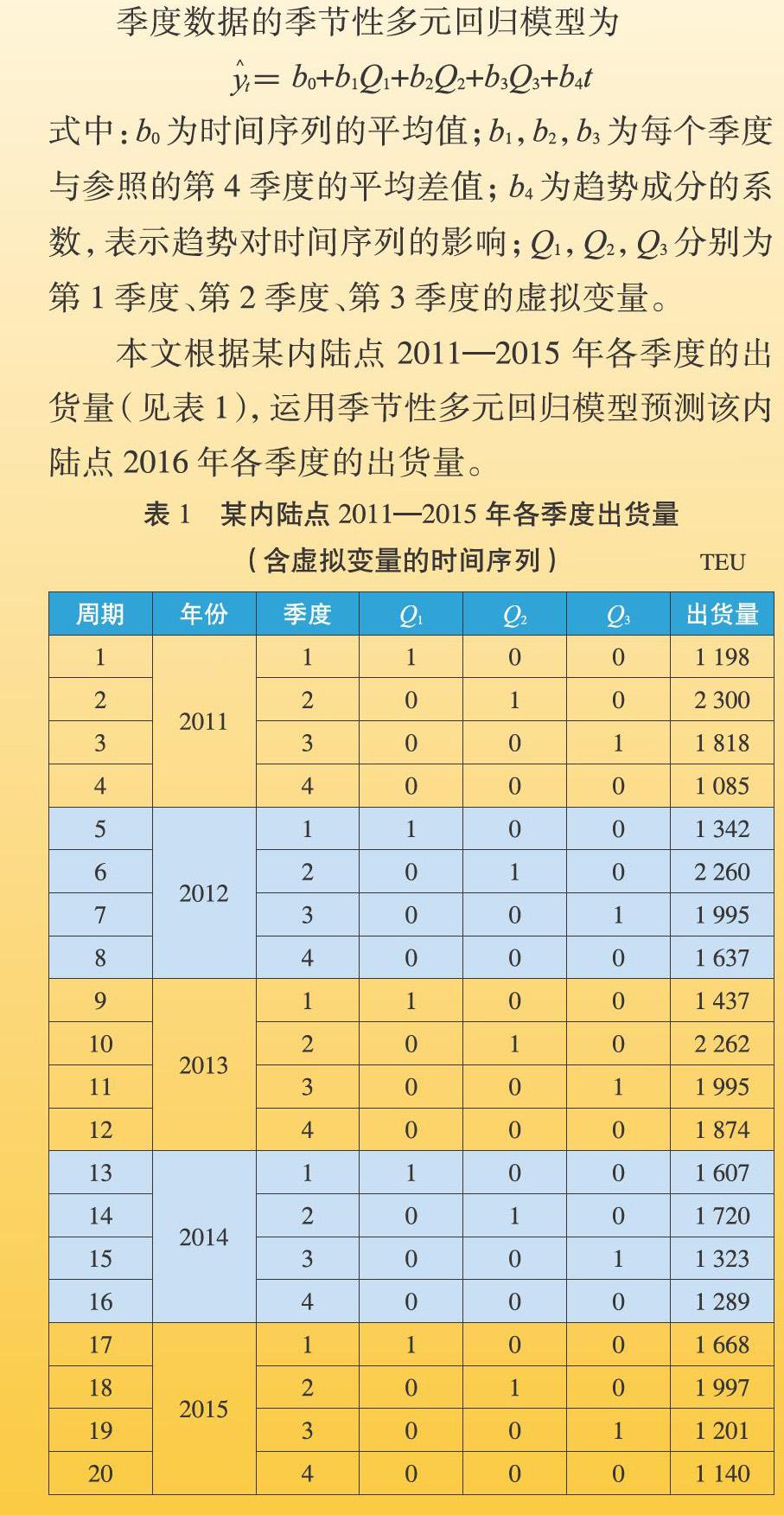
季度数据的季节性多元回归模型为
=b0+b1Q1+b2Q2+b3Q3+b4t
式中:b0为时间序列的平均值;b1,b2,b3为每个季度与参照的第4季度的平均差值;b4为趋势成分的系数,表示趋势对时间序列的影响;Q1,Q2,Q3分别为第1季度、第2季度、第3季度的虚拟变量。
本文根据某内陆点2011―2015年各季度的出货量(见表1),运用季节性多元回归模型预测该内陆点2016年各季度的出货量。
对模型求解,得到回归方程为
据此预测2016年各季度出货量,得到第1季度出货量为,第2季度出货量为,第3季度出货量为,第4季度出货量为。
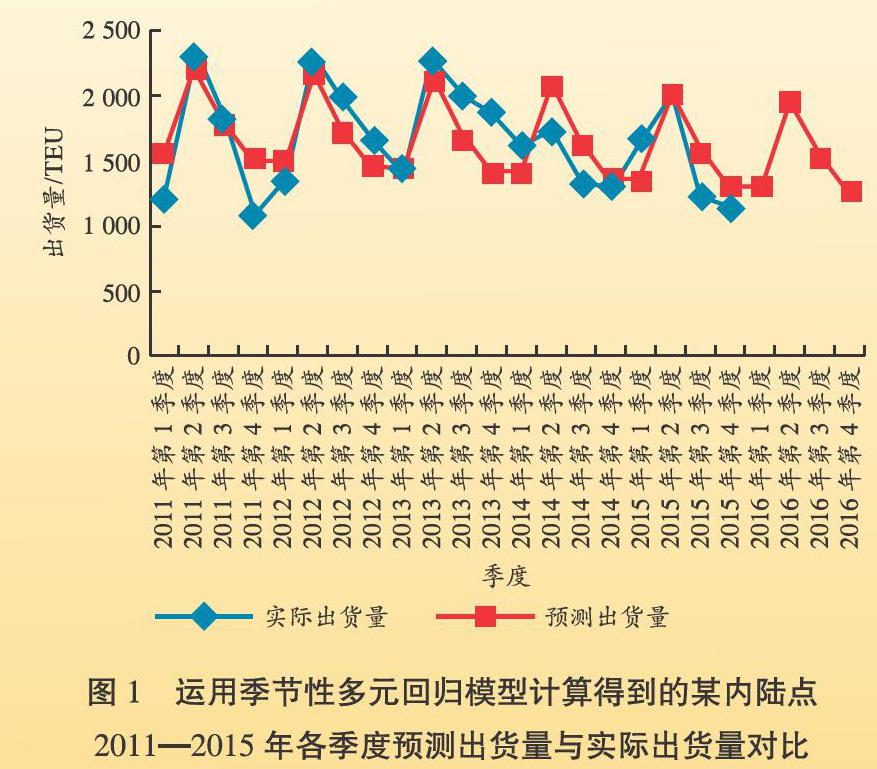
在上述回归分析中,评估参数R Square和Adjusted R Square的数值偏低,均在0.5左右;评估参数Significance F的数值小于5%,接近于0;评估参数P-value的数值并非都小于5%。以上结果说明该模型的拟合度不理想,导致预测出货量与实际出货量之间有较大差距(见图1)。
3 时间序列分解模型在内陆出货量预测中的应用
时间序列预测的另一个常用模型是时间序列分解模型,具体方法如下:首先,计算季节指数,以确定时间序列中的季节因素;然后,将季节因素从时间序列中分离出去,以消除季节性;最后,对消除季节因素的时间序列建立预测模型并计算预测值,再回归相应的季节指数。[5]
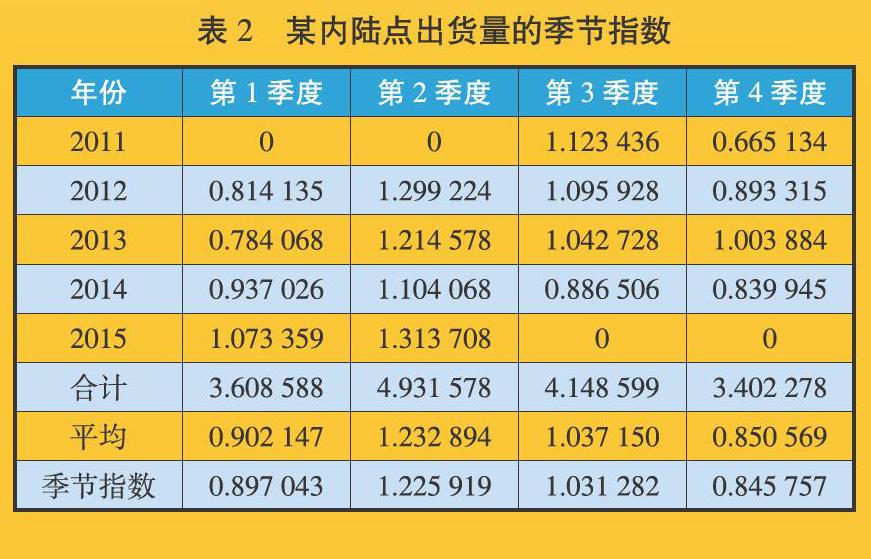
季节指数指某一季度的数据与全年平均数据的比值,季节变动的程度根据各季节指数与其平均数(100%)的偏差程度来测定。为求得季节指数,对季节数据进行4项移动平均,并对结果进行中心化处理,计算移动平均的比值,即季节指数。某内陆点出货量的季节指数如表2所示,分离季节因素后该内陆点出货量的时间序列如图2所示。
式中:为分离季节因素后的预测出货量;b0为趋势线在纵坐标上的截距;b1为趋势线的斜率,表示时间周期变动1个单位时观察值的平均变动数量;t为时间周期。为使b0和b1的数值最优,需要使每一周期时间序列的预测值与观察值的误差平方和最小化。令Tt为第t周期时间序列的观察值,一般模型为
经计算,得到此模型的最优解为b0=1 770.1,b1=Ha10.731,因此,线性趋势方程为
利用该线性趋势方程计算得到分离季节因素后的预测出货量,然后回归相应的季节指数,得到最终的预测出货量。
由图3可见,运用时间序列分解模型得到的预测出货量与历史数据非常吻合,说明该模型对季节性货量的预测效果优于季节性多元回归模型。建议运用时间序列分解模型预测内陆进出口箱量,并综合考虑长假、运力调配、工厂检修等影响因素,据此确定内陆存箱量。
参考文献:
[1] 安德森D R,斯威尼D J,威廉斯T A,等. 数据、模型与决策:管理科学篇[M]. 侯文华,译. 北京:机械工业出版社,2012:441-465.
[2]鞠美晨. 基于无水港的集装箱配备与空箱调运问题研究[D]. 大连:大连海事大学,2013.
[3] 张军. 平衡为王[J]. 中国远洋航务,2006(8):40-41.
[4]贾俊平. 统计学[M]. 北京:中国人民大学出版社,2004:323-386.
[5] 宋若辰. 班轮公司集装箱空箱在途库存控制研究[D]. 上海:上海交通大学,2012.
(编辑:张敏 收稿日期:2016-04-21)

