求解非线性方程组的一种非精确Broyden方法*

伍佩钰 张丽

（长沙理工大学数学与统计学院，长沙，410004）

考虑如下非线性方程组

基于文献［8］中的精确Broyden方法，我们提出如下求解问题（1.1）的非精确　Broyden方法.

算法1 （非精确Broyden方法）

步1：若F（xk）=0，则算法停止.否则，按（2.1）和（2.2）非精确求解线性方程组BkP　+ F（xk）=0，得到其近似解pk：

求解非线性方程组的一种非精确Broyden方法*

伍佩钰 张丽

（长沙理工大学数学与统计学院，长沙，410004）

本文提出了求解非线性方程组的一种非精确Broyden方法.该方法是文献［8］中精确Broyden方法的推广.在适当的条件下，我们证明了非精确Broyden方法具有全局收敛性和超线性收敛性.数值实验表明，该方法效果较好.

非线性方程组 非精确Broyden方法 全局收敛 超线性收敛

1　引言

考虑如下非线性方程组

其中F=（F1，F2，…，Fn）T：Rn→Rn是连续可微的函数.

关于问题（1.1）的数值方法研究是计算数学与优化领域的重要课题［1，5，6］.对于中小型问题，牛顿法、拟牛顿法等都是行之有效的方法［10］.Broyden方法是求解方程组（1.1）的一种重要的拟牛顿方法.1965年，Broyden［2］第一次提出求解非线性方程组的拟牛顿法，因其好的局部收敛性［2，3，4］，很快受到学者们的青睐，但是对求解非线性方程组的全局收敛性的结果却较少.Griewank［7］在1986年研究了非线性方程组的Broyden方法的全局收敛性，并提出了一种无导数的线性搜索，同时证明了Broyden方法在该线性搜索下的全局收敛.Li和Fukushima［8］构造了一个反例表明Griewank的线性搜索是不适定的.为克服此缺陷，Li和Fukushima［8］提出了一种称为近似范数下降的无导数线性搜索，在适当的条件下，证明了求解非线性方程组Broyden方法的全局收敛性.但该方法中每一步都要精确求解一个线性方程组BkP+F（xk）=0，当方程组（1.1）的变量个数比较多时，精确求解该子问题的计算量较大.

本文提出了一种非精确Broyden方法，对子问题进行非精确求解，在适当的条件下，我们证明了算法具有全局收敛性和超线性收敛性.

2　算法

基于文献［8］中的精确Broyden方法，我们提出如下求解问题（1.1）的非精确Broyden方法.

算法1 （非精确Broyden方法）

步1：若F（xk）=0，则算法停止.否则，按（2.1）和（2.2）非精确求解线性方程组BkP+ F（xk）=0，得到其近似解pk：

其中

步2：若

成立，则令λk=1，转步4.

步3：按如下线性搜索计算步长因子λk，即λk=max｛1，β，β2，…｝满足不等式

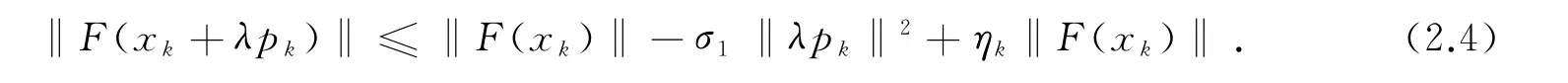
步4：令xk+1=xk+λkpk.

步5：按如下Broyden修正公式计算Bk+1：

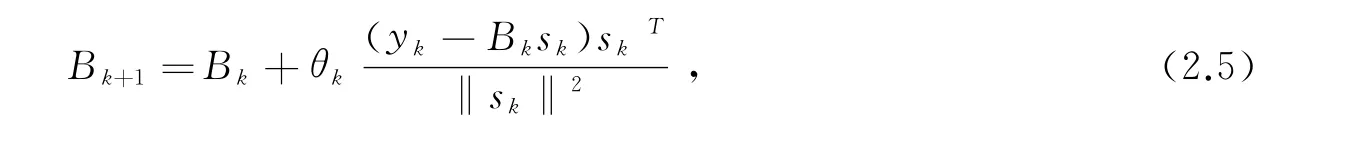
步6：令k=k+1，转步1.

注记 ①在步1中，若对任意k，rk=0，则算法1退化为文献［8］中的精确Broyden方法.②不等式（2.4）对任意充分小的λ＞0恒成立，且对任意k有

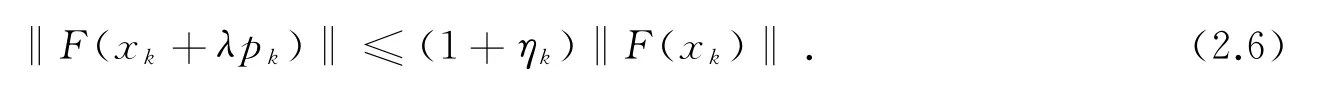
3　全局收敛性

为了得到算法1的全局收敛性，做如下假设假设A

（ii）F′（x）在Ω上Lipschitz连续，即存在常数L＞0，使得

（iii）对∀x ∈Ω，F′（x）非奇异.

类似于文献［8］中的证明，我们有如下引理.

引理1［8］由算法1产生的序列｛xk｝⊂Ω.

证明 由（2.6）可得，对任意的k有

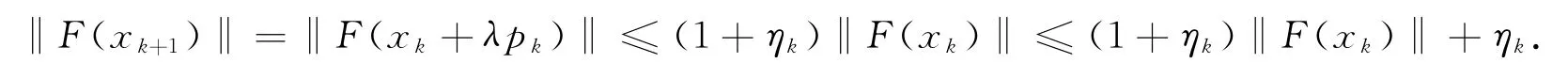
由（2.3）和（2.4）可得，对任意的k有

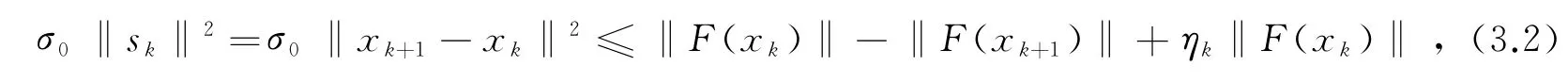
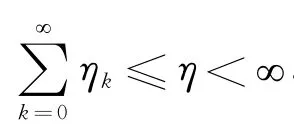
引理4［8］设正数序列和满足

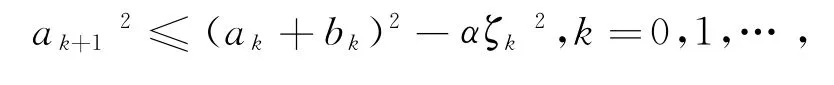
为了后续的分析，记

则yk=Ak+1sk，代入（2.5）得

定义

由yk=Ak+1sk，得

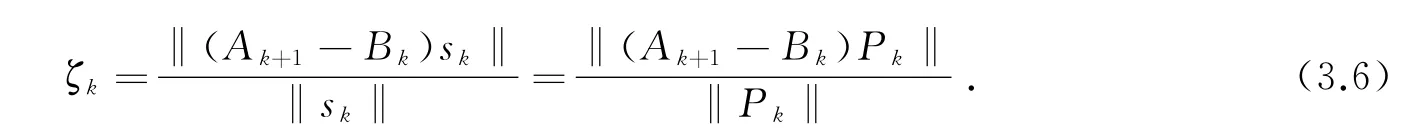
引理5［8］设假设A中（i）和（ii）成立，且xk｛｝由算法1产生.

特别地，存在｛ζk｝的一个子列收敛于0.

下面证明算法1的全局收敛性.

定理1 设假设A成立，则算法1产生的点列xk｛｝收敛于问题（1.1）的唯一解.

情况一：若有无穷多个k，λk由（2.3）确定，记这无穷多个k构成的集合为K=｛i1，i2，…｝.则当k ∈K时，‖F（xk+1）‖≤ρ‖F（xk）‖；当k ∉K时，由（2.4）得‖F（xk+1）‖≤（1+ ηk）‖F（xk）‖；

情况二：设对充分大的k，λk由（2.4）确定，设Ak+1由（3.3）定义，ζk由（3.5）定义.

由（3.1）及引理5知，存在｛ζk｝的子列｛ζk｝k∈K收敛于0，因｛xk｝k∈K⊂Ω有界，不妨假设序列收敛于x-，又由（3.1）得sk=xk+1-xk→0，则｛Ak+1｝k∈K收敛于F′（x-），因此存在常数M1＞0，对∀k ∈K充分大时‖Ak+1‖-1≤M1，由（2.1）和（3.6）知

故存在常数C1＞0，使得对∀k∈K充分大时，有

又因u0＜1，得到F（x-）=0.证毕.

4　超线性收敛

下面证明超线性收敛性，为此先证明如下引理.

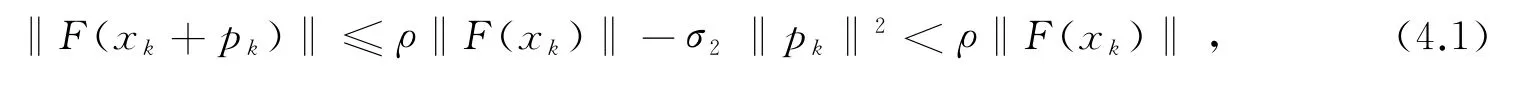
证明 由算法1中的步2，可得存在一个常数ζ＞0，使得当ζk≤ζ且k充分大时（4.1）成立.由定理1可得xk｛｝收敛于问题（1.1）的唯一解x*，且存在一个常数M2＞0，对充分大的k，使得‖Ak+1‖-1≤M2.类似于（3.11）的证明，存在一个常数ζ′＞0，C2＞0，当ζk≤ζ′且k充分大时，有

由（2.1）可得

从而有

其中M3＞0为在Ω中的一个上界，且第二个不等式由（3.6）推得，第三个不等式由（4.2）推得.由此可得

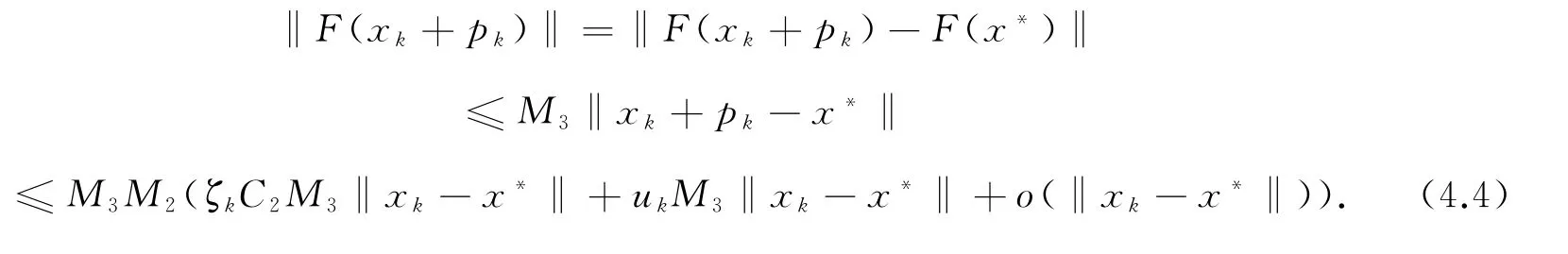
又由F′（x*）的非奇异性与xk→x*，则存在常数m＞0，对所有充分大的k，使得成立.

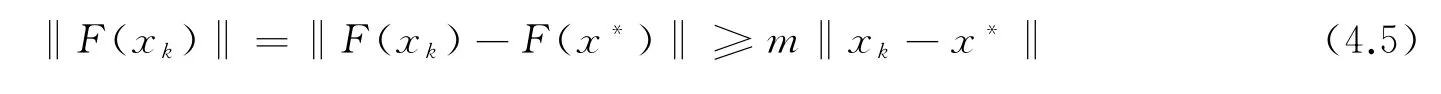
由（4.2），（4.4），（4.5）可得，当ζk≤ζ′时，

下面证明算法1的超线性收敛性.

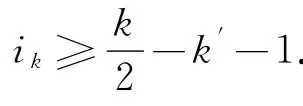
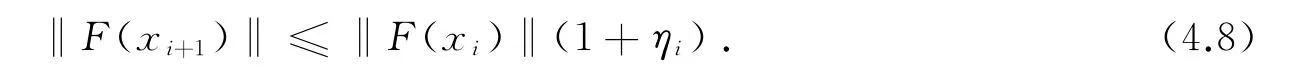
当i∉Ik时，取i从k′到k，则有

5　数值实验及结果分析

我们对算法1进行数值实验，检验其数值结果.利用MATLAB7.0编程，程序在3.2GHZ处理器，2GB内存的电脑上实现.算法终止条件为‖F（xk）‖≤10-4，问题（2.1）的求解采用Matlab中的GMRES（A，B，RESTART，TOL）计算.数值结果见下表，表中：n表示测试问题的维数，iter表示算法迭代的次数，‖F（xk）‖表示终止时剩余范数，time表示算法计算所需时间（单位为秒）.

测试问题如下：

问题1 离散的两点边界值问题［11］：

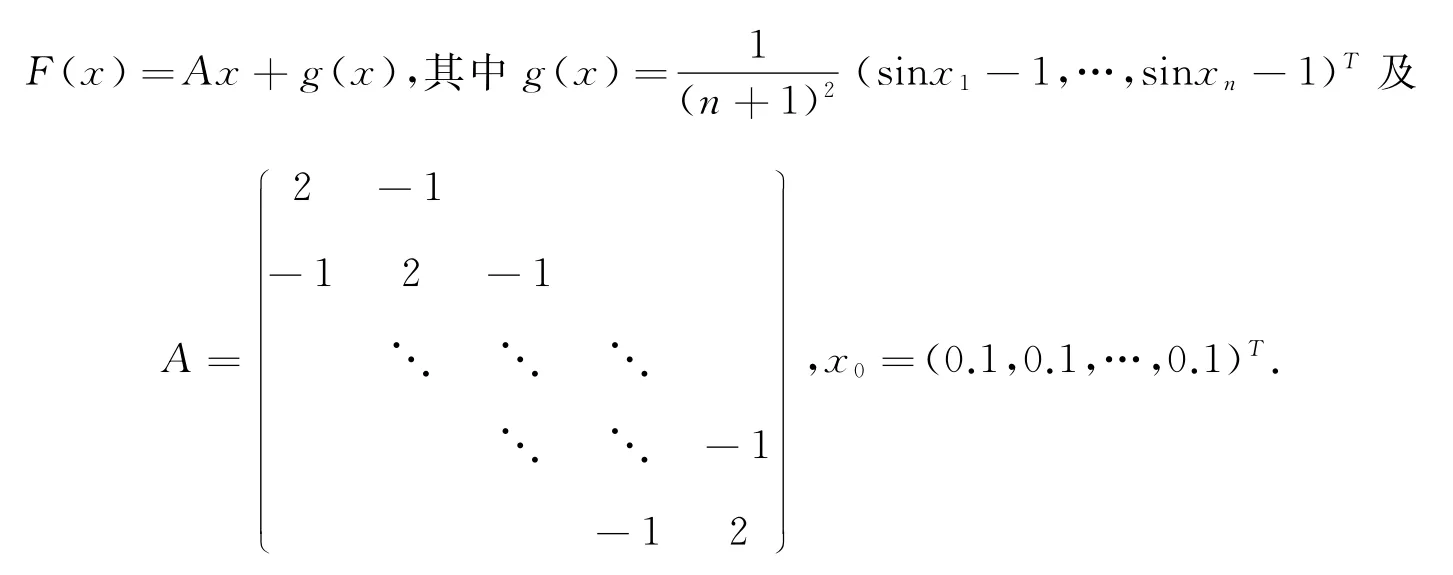
问题2 F由下式定义［12］：

实验结果如下：

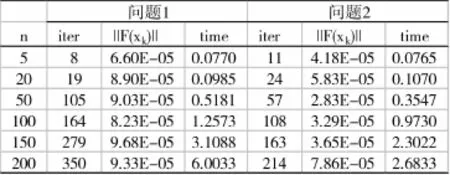
上表的数值结果表明，非精确Broyden方法成功求解问题1和问题2，当问题的维数较大时，需要迭代的次数和计算的时间也增加，问题2比问题1的数值表现更好.总的来说，我们的非精确Broyden方法效果较好.

［1］袁亚湘，孙文瑜.最优化理论与方法［M］.北京：科学出版社，2001，12-130.

［2］Broyden C.G.，A class of methods for solving nonlinear simultaneous equations［J］.Mathematics of Computation，1965，19（2）：57-593.

［3］Dennis J.E.，MoréJ.J.，A characterization of superlinear convergence and its application to quasi-Newton methods［J］.Mathematics of Computation，1974，8（2）：549-560.

［4］Broyden C.G.，Dennis J.E.，MoréJ.J.，On the local and superlinear convergence of quasi-Newton methods［J］.Journal of Institute of Mathematics and Applications，1973，12（1）：223-246.

［5］Dennis J.E.，Schnabel R.B.，Numerieal methods for uneonstrained Optimization and nonlinear equations［M］.Englewood Cliffs：Prentiee-Hall Press，1983，10-180.

［6］Ortega J.M.，Rheinboldt W.C.，Iterative solution of nonlinear equations in several variables［M］.Beijing：Academic Press，1970，1-200.

［7］Griewank A.，The’global’convergence of Broyden-like methods with a suitable line search.Austral［J］. Anziam Journal，1986，28（1）：75-92.

［8］Li D.H.，Fukushima M.，A Derivative-Free line Search and Global Convergence of Broyden-like Method for Nonlinear Equations［J］.Optimization Methods and Software，1999，13：181-201.

［9］Li D.H.，Fukushima M.，Smoothing Newton and Quasi-Newton Methods for Mixed Comple-mentarity Problems［J］.Computational Optimization and Applications，2000，17：203-230.

［10］周伟军.拟牛顿法及其收敛性：［湖南大学博士学位论文］.长沙：湖南大学，2006，9-16.

［11］Li D.H.，Fukushima M.，A globally and superlinearly convergent Gauss-Newton based BFGS method for symmetric nonlinear equations.SIAM Journal on Numerical Analysis，1999，37（1）：152-172.

［12］Li Q.，Li D.，A class of derivative-free methods for large-scale nonlinear monotone equations.IMA Journal of Numerical Analysis，2011，31（4）：1625-1635.

An Inexact Broyden Method for Nonlinear Equations

Wu Peiyu Zhang Li
（School of Mathematics and Statistics，Changsha University of Science and Technology，Changsha 410004，China）

This paper introduces an inexact Broyden method for solving nonlinear equations，which is an extension of the method in［8］.Under appropriate conditions，we prove that the proposed method converges globally and superlinearly.Numerical results are given to show its efficiency.

Nonlinear equations Inexact Broyden method Global convergence Superlinear convergence

湖南省自然科学基金项目（14JJ3084）和湖南省教育厅科学研究项目（13B137）资助

2016年05月30日