2m阶差分方程边值问题解的存在性
周 展, 徐 菲
(广州大学 a.数学与信息科学学院; b. 数学与交叉科学广东普通高校重点实验室, 广东 广州 510006)
2m阶差分方程边值问题解的存在性
周展, 徐菲
(广州大学 a.数学与信息科学学院; b. 数学与交叉科学广东普通高校重点实验室, 广东 广州510006)
讨论一类2m阶非线性差分方程边值问题.通过建立相应的变分框架,将边值问题的解转换为对应的非线性泛函的临界点.利用环绕定理,获得变分泛函临界点的存在性,进而得到所求边值问题解的存在性.最后给出例子说明本文的结论.
2m阶差分方程; 环绕定理; 边值问题
0 引 言
差分方程在诸如物理、生态、金融等领域有着广泛的应用.众所周知,差分方程是微分方程离散化, 它与相应的微分方程有很多共同的性质,但很多差分方程与其对应的微分方程有本质不同.因此,在过去几十年里,许多学者把注意力放在差分方程周期解的存在性、振动性、边值问题等方面,获得了丰富的结果,主要方法包括上下解方法、拓扑度理论、不动点理论等经典方法[1-4].2003 年开始,GUO等开始利用临界点理论研究二阶超线性差分方程的周期解和次调和解[3],后来,这一方法被用来研究差分方程的边值问题.
设R,Z分别表示实数集和整数集.对任给的a,b∈Z且a≤b,定义Z(a,b)={a,a+1,…,b},Z(a)={a,a+1,…}.Δ为向前的差分算子,定义为Δun=un+1-un,Δkun=Δ(Δk-1un),k∈Z(2).设T∈Z(2), 在参考文献[5]中,ATICI等讨论了如下差分方程的周期边值问题:
(1)
这里f∈C(Z(1,T)×R,R).方程(1)作为一个二阶微分方程的离散模型,被应用于很多领域,如空气动力学、核物理等.运用上下解方法,ATICI等建立了边值问题(1)存在唯一解的条件.
2014年, LIU等在参考文献[6]中利用临界点理论研究了四阶差分边值问题
(2)
的解的存在性与不存在性条件.其中δ表示正奇数的比,f∈C(Z(1,T)×R, R).在物理学中方程(2)经常被用来模拟弹性梁的弯曲程度.2009年,ZOU等在参考文献[7] 中利用临界点理论讨论了以下2m阶差分方程:
Δm(pn-mΔmun-m)+(-1)m+1f(n,un)=0,
n∈Z(1,T)
(3)
在边值条件
(4)
下的解的存在情况.其中T和m是任给的正整数,且T>m.然而,可以看到大部分参考文献[5-6,8-12]都是研究二阶或者四阶差分方程的, 对一般高阶差分方程的研究相对来说较少.受文献[4-7,13]的启发,本文讨论更一般的2m阶差分方程
Δm(pn-mΔmun-m)+(-1)m+1Δ(g(Δun-1))+
(-1)m+1f(n,un)=0,n∈Z(1,T)
(5)
在边值条件
(6)
下的解的存在性.其中g∈C(R,R),f(n,·)∈C(R,R)对任意n∈Z(1,T).
1 准备工作
设m,T∈Z(1)且T>m, 定义向量空间Ω={u={un}|un∈R,n∈Z(1-m,T+m)},对任意的u,v∈Ω,a,b∈R有au+bv={aun+bvn}.E={u={un}∈Ω|u1-i=u1,uT+i=uT,i∈Z(1,m)}是Ω的一个线性子空间.易知E与RT是同构的,因此,在空间E上可以定义内积如下:

(7)
由E上的内积可以诱导空间E上的范数:
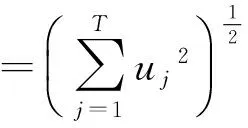
(8)
对任意的r≥1, 可以定义空间E上的另一种范数:

(9)
因为E是有限维空间,所以存在2个常数c2(r)≥c1(r)>0使得
c1(r)‖u‖2≤‖u‖r≤c2(r)‖u‖2,∀u∈E
(10)其中,‖u‖=‖u‖2.下面建立与边值问题(5)~(6)相对应的变分框架.对任给的u={un}n∈Z(1-m,T+m)∈E, 定义E上的泛函
(11)


f(n,un),∀n∈Z(1,T).
因此,u是泛函J的一个临界点当且仅当u满足边值问题(5)~(6).记u={un}∈E,由于E与RT同构,所以u可写成u=(u1,u2,…,uT)*∈RT.那么存在T×T阶矩阵A使得
(12)
显然, A是一个半正定矩阵.令σ+(A)为A的所有正特征值构成的集合.定义

设W,Y分别为A的0特征值和所有正特征值对应的特征向量空间,则
W={(u1,u2,…,uT)*∈RT|ui=w,
w∈R,i∈Z(1,T)},
且
RT=W⨁Y.
下面介绍一些临界点理论的基本概念和基本结果.
定义1设S是一个实Banach空间,J∈C1(S,R)满足Palais-Smale条件 (简称P.S.条件), 如果对任给的{un}⊂S,{J(un)}有界,当n→∞时J′(un)→0蕴含{un}有收敛的子列.

引理1(环绕定理[14])设S=S1⨁S2是一个Hilbert空间, 其中,S1是S的一个有限维的子空间. 若J∈C1(S,R)满足P.S.条件且满足:
(1)存在常数σ>0和ρ>0使得J|∂Bρ∩S2≥σ;
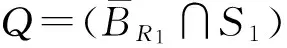

2 主要结论及其证明
定理1如果以下假设都满足:
(A1)f(n,v),g(v)是关于v连续, 且g(0)=0,G(v)≥0对v∈R成立,其中n∈Z(1,T);
(A2)对任给的n∈Z(1-m,T),pn>0;

(A4)存在正常数R2和β>2使得0<βF(n,v)≤vf(n,v),n∈Z(1,T),|v|≥R2;
(A5)存在正常数R3和α<β使得0 那么边值问题(5)~(6)至少存在2个非平凡解. 记 p*=max{pn,n∈Z(1-m,T)}, p*=min{pn,n∈Z(1-m,T)}. 则p*≥p*>0. 为了方便定理1的证明, 需要验证下面的引理. 引理2假设(A1)~(A5)都满足, 那么泛函J满足P.S.条件. 证明设{u(l)}l∈Z(1)⊂E是一个P.S.序列,则存在常数C使得|J(u(l))|≤C,∀l∈Z(1).根据式(11),注1和注2有 (13) 注意到J(u(l))≥-C, 则由式(13)得 因为β>max{2,α}, 所以存在常数N0>0使得‖u(l)‖≤N0,∀l∈N. 因此, {u(l)}是E上的有界序列.因为E是有限维的, 所以 {u(l)}存在收敛的子列.即J满足P.S.条件. (14) 定义 例1设T为一正整数, 考虑四阶差分方程边值问题 (15) Δu-1=Δu0=0,ΔuT=ΔuT+1=0 (16) 对照式(5), 有 m=2,pn≡1,g(s)=s3,f(n,v)=n2v5, 因此 易知边值问题(15)~(16)满足条件(A1)~(A5), 其中α=4,β=6, 由定理1 知至少存在2个非平凡解. [1]AGARWAL R P, O′REGAN D. Singular discrete (n,p) boundary value problems[J]. Appl Math Lett, 1999, 12(8): 113-119. [2]AGARWAL R P, WONG F H. Upper and lower solutions method for higher-order discrete boundary values problems[J]. Math Ineq Appl, 1998, 1(4): 551-557. [3]GUO Z M, YU J S. Existence of periodic and subharmonic solutions for second-order superlinear difference equations[J]. Sci China Ser A, 2003, 46(4): 506-515. [4]ZHOU Z, YU J S, CHEN Y M. Periodic solutions of a 2nth-order nonliner difference equation[J]. Sci China Math, 2010, 53(1): 41-50. [5]ATICI F M, CABADA A. Existence and uniqueness results for discrete second-order periodic boundary value problems[J]. Comput Math Appl, 2003, 45(6/9): 1417-1427. [6]LIU X, ZHANG Y B, SHI H P. Nonexistence and existence results for a class of fourth-order difference Neumann boundary value problems[J]. Indag Math, 2015, 26(1): 293-305. [7]ZOU Q R, WENG P X. Solutions of 2nth-order boundary value problem for difference equation via variational method[J]. Adv Differ Equ, 2009, Art. ID 730484,10pp. [8]李龙图, 翁佩萱. 二阶泛函差分方程边值问题[J]. 华南师范大学学报:自然科学版, 2003(3): 20-24. LI L T, WENG P X. Boundary value problems of second order functional difference equation[J]. J South China Normal Univ: Nat Sci Edi, 2003(3): 20-24. [9]梁海华, 翁佩萱. 一类四阶差分边值问题解的存在性与临界点方法[J]. 高校应用数学学报, 2008, 23(1): 67-72. LIANG H H, WENG P X. Existence of solutions for a fourth-order difference boundary value problem and critical point method[J]. Appl Math J Chin Univ Ser A, 2008, 23(1): 67-72. [10]ZHENG B, ZHANG Q Q. Existence and multiplicity of solutions of second-order difference boundary value problems[J]. Act Appl Math, 2010, 110(1): 131-152. [11]LIU X, ZHANG Y B, SHI H P. Periodic solutions for fourth-order nonlinear functional difference equations[J]. Math Meth Appl Sci, 2015, 38(1): 1-10. [12]LIU X, ZHANG Y B, SHI H P. Nonexistence and existence results for a class of fourth-order difference Dirichlet boundary value problems[J]. Math Meth Appl Sci, 2015, 38(4): 691-700. [13]BONANNO G, CANDITO P, D′AUGI G. Variational methods on finite dimentional banach spaces and discrete problems[J]. Adv Nonlin Stud, 2014, 14(4): 915-939. [14]RABINOWITZ P H. Minimax methods in critical point theory with applications to differential equations[M]. USA: CBMS, American Mathematical Society, 1986. 【责任编辑: 周全】 Existence of solutions to the boundary value problems of a 2mth-order difference equation ZHOU Zhan, XU Fei (a. School of Mathematics and Information Sciences; b. Key Laboratory of Mathematics and Interdisciplinary Sciences of Guangdong Higher Education Institute, Guangzhou University, Guangzhou 510006, China) Existence of solutions to the boundary value problems of a 2mth-order difference equation is considered in this paper. By establishing the corresponding variational structure, we transform the problem of the existence of solutions to the boundary value problems into the existence of the critical points for the corresponding variational functional. By using Linking Theorem, we obtain the existence of the critical points of the variational functional, and the existence of solutions of the boundary value problems is achieved as well. An illustrative example is presented at length to illustrate our conclusion. 2mth-order difference equations; Linking Theorem; boundary value problems 2016-01-27; 2016-05-08 国家自然科学基金资助项目(11571084);广州市“121人才梯队工程”资助项目 周展(1965-),男,教授,博士.E-mail: zzhou@gzhu.edu.cn 1671- 4229(2016)04-0013-05 O 175.8 A




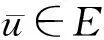

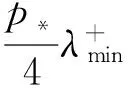








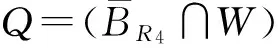

3 例题


