OFDM放大转发中继系统信息与能量同传优化算法研究

黄高飞， 郑　晖, 赵　赛, 唐　冬

(广州大学 机械与电气工程学院，广东 广州　510006)



OFDM放大转发中继系统信息与能量同传优化算法研究

黄高飞， 郑晖, 赵赛, 唐冬

(广州大学 机械与电气工程学院，广东 广州510006)

信息与能量同传是解决无线通信网络能量受限问题的有效技术.文章针对能量受限无线中继的OFDM放大转发中继系统，研究信息与能量同传的快速优化算法，在提高系统端到端传输速率性能的同时，延长中继结点电池的使用寿命.①研究了OFDM放大转发中继系统的最优能量传输和子载波配对方案；②将信息传输功率分配和能量传输时间优化问题形成为具有非凸目标函数和非凸能量收集约束的非凸优化问题；③通过分式规划问题优化方法和CCCP (Constrained Concave Convex Procedure)方法对该非凸优化问题进行求解，提出了相应的资源分配优化算法.仿真结果表明，与已有算法相比，文章提出的资源分配优化算法可明显提高信息与能量同传OFDM AF中继系统的速率性能.

信息与能量同传； 正交频分复用(OFDM)； 中继； 资源分配； 分式规划

能量收集是解决无线通信网络能量受限问题的新技术，其中利用光、风、热、频谱环境及机械振动等周边自然资源收集能量的新方法倍受重视.然而，研究表明，此类从周围环境进行能量收集的技术属于被动式能量收集，其效率和有效性受到各种环境因素的影响，可靠性往往比较差.近年来，学界开始关注主动式的无线能量传输技术，即通过近场电感耦合、电磁共振耦合、射频远场传输和激光能量传输等方式，实现持续稳定的供电.其中，利用射频远场传输(RF，Radio-Frequency)信号进行能量收集，具有成本低、无距离限制等优点，因此,得到了学者们的重点关注[1-2].此外，射频信号除了可携带能量之外，还可以承载信息，因此，能量和信息可以通过无线方式同时传输，由此产生了一种能量收集的新技术——信息与能量同时无线传输[2](简称信息与能量同传，Simultaneous Wireless Information and Power Transfer)技术.通过射频信号同时传输信息和能量，射频能量传输无需特定的频带，因此，可以充分利用有限的能量和带宽的同时，有效控制对通信系统的干扰.作为一种新兴技术，信息与能量同传有望在提高无线传输系统性能的同时，有效地解决无线网络中的能量消耗问题[3-6].

无线中继以低成本改善无线通信网络的覆盖和提高容量，是新一代无线通信网络的关键技术.然而，在许多应用场合(如无线传感器网络)中，由于无线中继结点使用容量有限的电池供电，工作寿命短，因此,无线中继的应用受到很大限制.在无线中继系统中结合信息与能量同传技术，装配无线射频能量收集电路的中继结点，一方面可接收源端发送的数据信息，另一方面，也可通过源端发送的射频信号进行能量收集，并利用收集到的能量转发数据信息，可有效地延长中继结点电池的使用寿命，近年来得到了学者们的广泛关注[7-9].LI等[3]针对单载波无线能量收集中继，提出了时分(TS，Time Switching)中继和能分(PS，Power Splitting)中继2种通信协议.其中，时分中继按时间先后进行能量收集和信息接收，即先从源端发射的射频信号收集能量，然后接收源端需转发的信息.而能分中继则是同时进行能量收集和信息接收，即把源端发送的信号一部分能量进行分离用于能量收集，剩余的能量用于信息接收.与能分中继相比，时分中继的能量收集电路和信息转发电路可单独设计，在实现上难度更小，近2年得到了学者们的广泛关注.在此基础上，NG等[4]和ZHOU等[5]针对解码转发(DF，Decode and Forward)时分中继，进一步研究了多载波OFDM中继系统的信息与能量同传资源分配优化算法，但相关算法不能直接用于放大转发(AF，Amplify and Forward)OFDM中继系统.由此，本文针对时分中继的OFDM AF中继系统，研究信息与能量同传资源分配优化算法，目标是提高系统的端到端传输速率.首先，提出了OFDM AF中继系统的最优能量传输和子载波配对方案；然后，把信息传输功率分配和能量收集时间联合优化问题形成为非凸问题，该问题的目标函数和中继能量收集约束均为非凸的，因此，无法通过传统的凸优化方法进行求解.为此，本文通过代数变换，把该问题转换为非线性分式规划问题[10]，并利用分式规划问题优化方法和CCCP(Constrained Concave Convex Procedure)方法[11]对该问题进行求解，从而提出了相应的资源分配优化算法.实验仿真结果表明，相对于已有算法，本文提出的资源分配算法可以显著提高系统的端到端传输速率性能.

1　系统模型

本文研究的OFDM AF 中继系统由源节点(S)、目的节点(D)和中继节点(R)组成，见图1.由于源与目的端距离较远或2者之间存在障碍物，目的端无法接收直接来自源端的信息，因此需由中继协助转发消息[3-5].源端配备固定的能源供应(如连接到电网)，而中继使用容量有限的电池从而能量受限.为延长中继电池使用寿命，中继需使用时分能量收集方式,从源端发送的射频信号收集能量，并利用收集到的能量转发源端发送的数据至目的端.

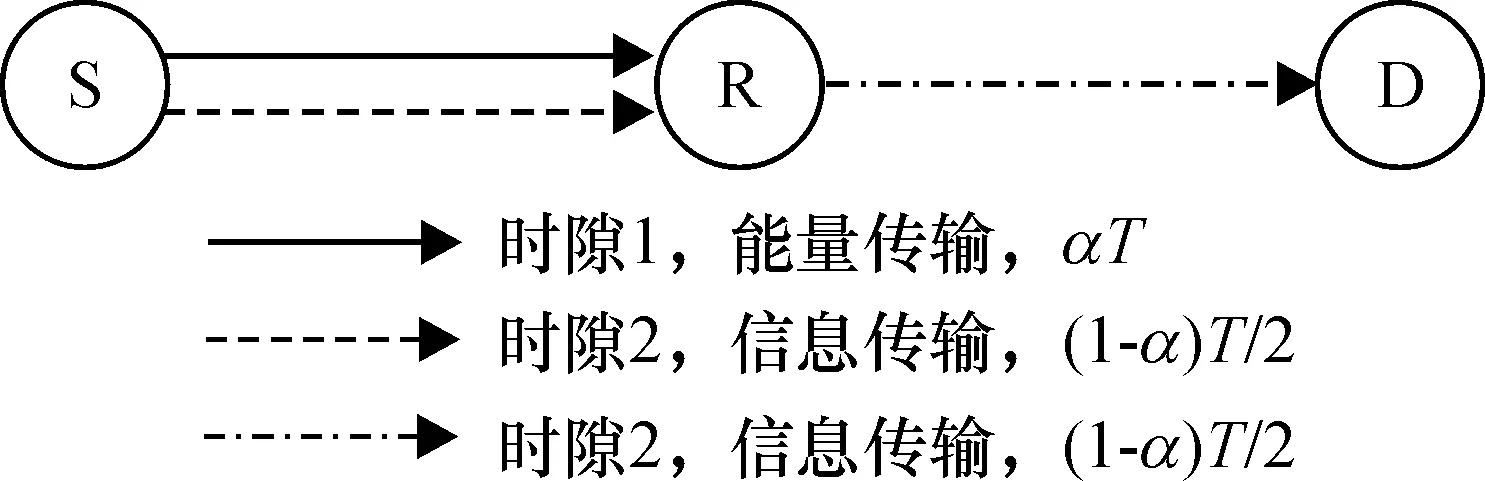
图1　系统模型

(1)

(2)

对信息与能量同传OFDMAF中继系统，以bps·Hz-1为单位的端到端信息传输速率可表示为[8]

(3)

因此，以最大化端到端系统传输速率为目标的资源分配问题可以表示为

(4)

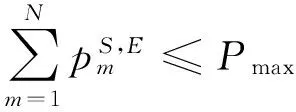
(5)

(6)

(7)

其中，Pmax为源的最大发射功率.

2　资源分配算法

2.1能量传输功率分配优化

在第1个时隙，源传输能量至中继.由式(1)，易得

(8)

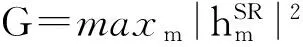
根据式(8),为使中继所收集的能量最大, 源应将所有可用功率分配至具有最大信道增益的子载波.因此,最优能量传输功率分配如下定理所述:

定理1对于信息与能量同传OFDMAF中继系统，式(4)的最优能量传输功率分配为

(9)

基于定理1，式(1)可以改写为

E=αGT

(10)

2.2子载波配对优化

当能量传输功率分配确定时，式(4)可简化为

(11)

(12)

(13)

对以上优化问题，当α给定时，式(11)等效于源和中继存在独立功率约束的传统OFDMAF中继系统的资源分配问题.ZHANG等[12]已证明传统OFDMAF中继网络的最优子载波配对为排序子载波配对，即源至中继链路最强信道增益的子载波与中继至目的端最强信道增益的子载波配对，源至中继链路次强信道增益的子载波与中继至目的端次强信道增益的子载波配对，以此类推.由此，可得以下定理：

定理2式(4)的最优子载波配对为排序子载波配对.

2.3能量收集时间及信息传输功率分配联合优化

在得到最优子载波配对后，式(11)仅包含能量收集时间和信息传输功率分配优化求解.然而，其目标函数和中继能量收集功率约束均是非凸的，因此式(11)是一个非凸优化问题，难以直接求解.

根据式(11)中继能量收集约束式(13)，可得

(14)

注意到式(7)的目标函数是一个关于α的单调非增函数，因此, α的最优解应满足

(15)

(16)

(17)

式(16)为非线性分式规划问题[10].为求解此问题，可把其改写为

min:μ

(18)

(19)

显然,式(18)可以改写为

min:μ

(20)

(21)

因此，当问题

(22)

(23)

的最优目标函数值非负时，μ即为问题(16)目标函数(即端到端传输速率)的上界.然而，由于问题(22)的目标函数为非凸的，因此问题(22)仍然是非凸的.为求解此问题，可把目标函数写为

(24)

其中函数

(25)

为2个凸函数的差，因此，问题(22)为差分凸优化问题，可利用CCCP(constrained concave convex procedure)方法[11]进行求解.为此，把Φ(pI)改写为以下凸函数：

(26)

其中，pI(k)为给定的初始值.根据文献[11]，问题(22)可通过图2所示算法迭代求解以下凸问题，得到其局部最优解：

(27)

(28)

当给定μ时，根据图2可求得式(22)的最优解.进一步地，根据分式规划问题求解方法，可通过Dinkelbach算法[11]得到式(16)的最优解.由此可得信息与能量同传OFDM AF中继系统的信息传输功率和能量收集时间联合优化算法，见图3.

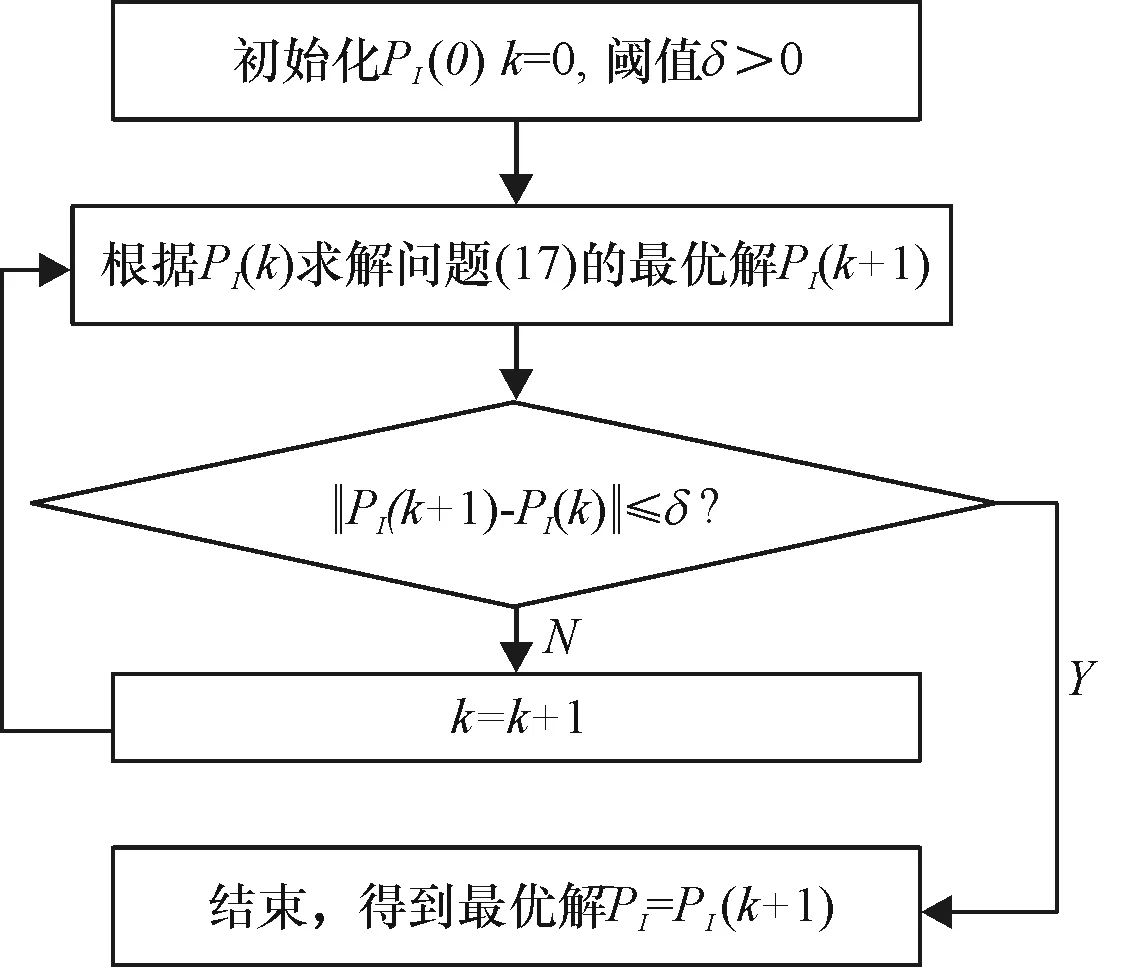
图2问题(13)的求解优化算法

图3信息与能量同传OFDM AF中继系统的信息传输功率和能量收集时间联合优化算法

Fig.3The joint information-transfer power and EH time optimization algorithm for SWIET-based OFDM AF relay systems

3　仿真结果

本节通过计算机仿真验证本文提出的资源分配算法的性能.仿真参数设置如下：子载波个数N=32,各个子载波的信道增益相互独立而且服从瑞利分布；大尺度路径损耗设为d-2，其中d是2个节点之间的距离，源与目的端的距离为10 m；源最大发射功率设置为pmax=10 mW，中继与目的端的接收噪声方差为10-6W；能量转换效率τ=0.9.

图4中继位置变化时不同资源分配方案的系统速率性能比较

Fig.4Rate performance comparison among different resource allocation schemes as relay location varies

图5给出了中继位置不同时，中继的最优能量收集时间比例α的值.图5可见，当中继位于源端附近(κ较小)或位于目的端附近(κ较大)时，中继用于能量收集的时间较少，而当中继位于源与目的端的中间位置时，中继用于能量收集的时间较多.

图5　中继位置变化时中继最优能量收集时间比例α的值

图6和图7进一步给出了当源最大发射功率pmax变化时，不同资源分配方案的系统速率性能比较以及中继的最优能量收集时间比例α的值.其中，κ取值为0.5.图6可见，随着源最大发射功率增加，端到端传输速率将增加.此外，图6的结果进一步验证了本文提出的优化方案可以取得比固定时分方案更大的系统速率.从图7可见，随着源最大发射功率增加，中继用于能量收集的时间将减少.

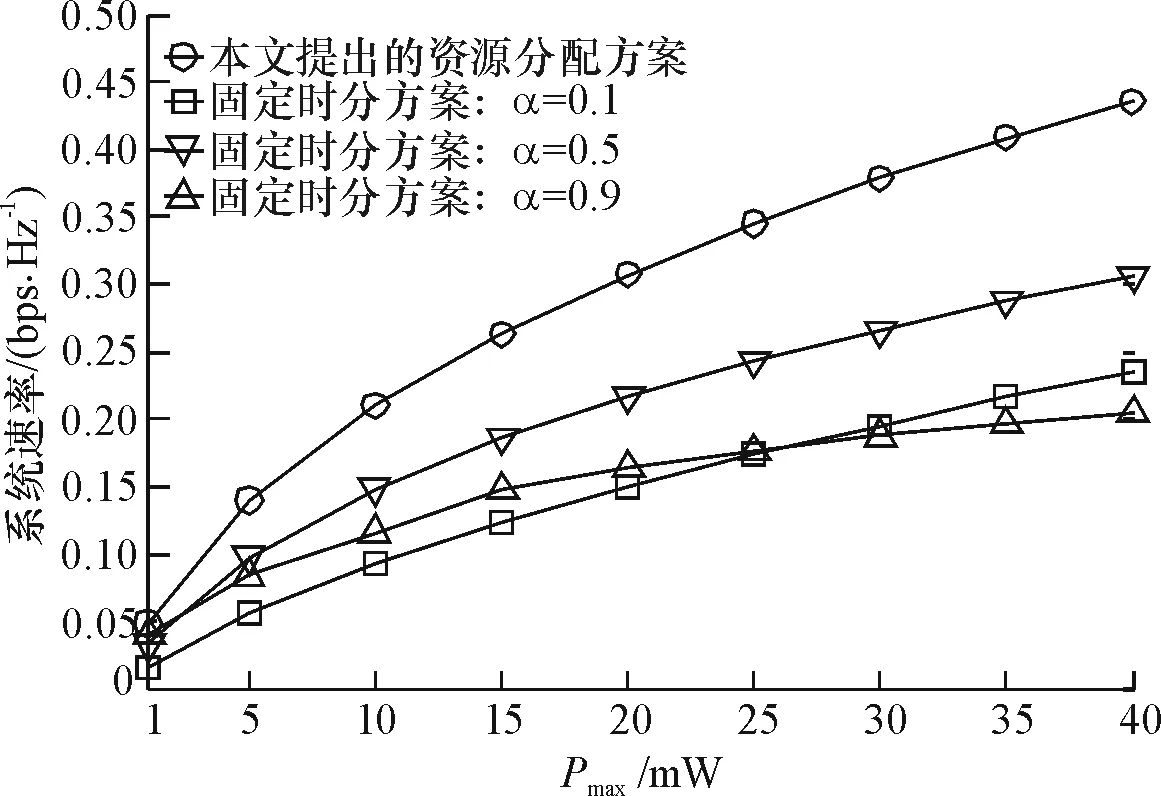
图6源最大发射功率变化时不同资源分配方案的系统速率性能比较

Fig.6Rate performance comparison of different resource allocation schemes as the maximum transmit power at source varies

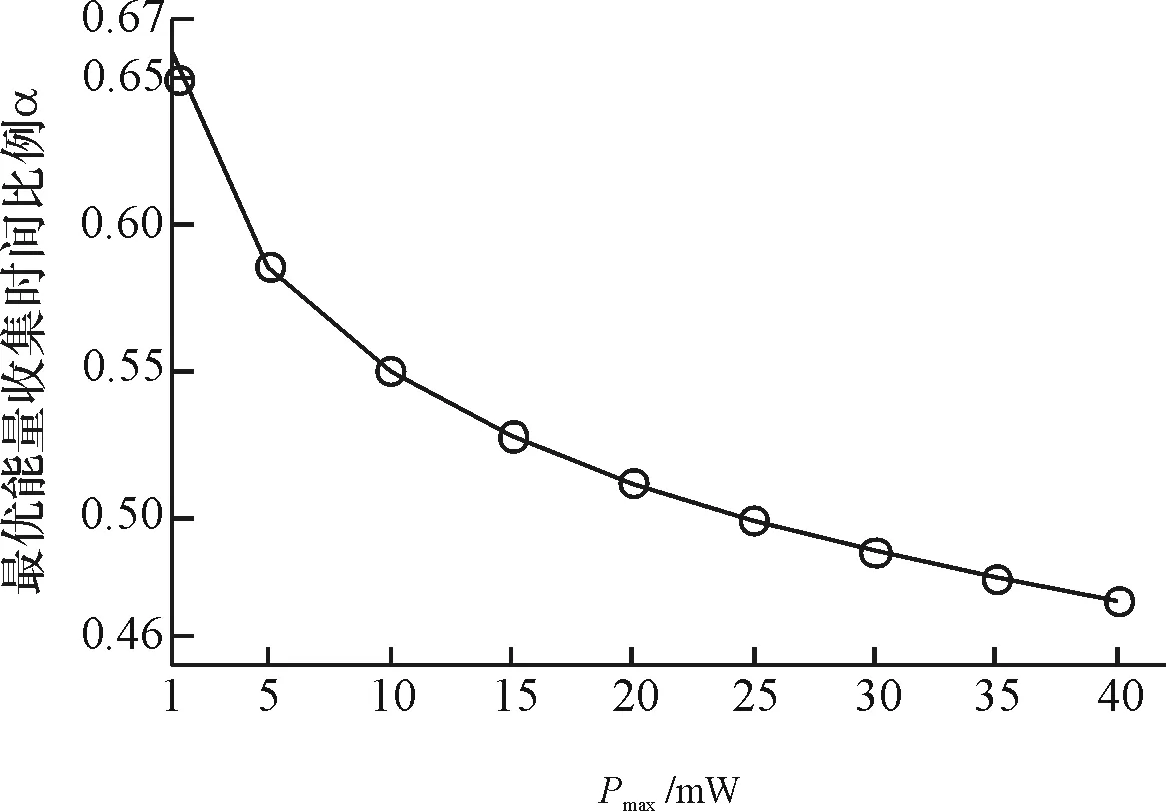
图7源最大发射功率变化时中继最优能量收集时间比例α的值

Fig.7The optimal EH time ratio as the maximum transmit power at source varies

4　结　论

本文研究了OFDM AF中继系统的信息与能量同传资源分配优化问题.①提出了最优能量传输和子载波配对方案；②把信息传输功率分配和能量传输时间联合优化问题形成为非凸问题，并通过分式规划问题优化方法和CCCP方法求解此非凸问题，从而提出了相应的资源分配优化算法.仿真结果表明，相对于已有资源分配算法，本文提出的资源分配算法可以获得更大的系统传输速率.

[1]HAN C, HARROLD T, ARMOU S, et al. Green radio: Radio techniques to enable energy-efficient wireless networks[J]. IEEE Commun Mag, 2011, 49(6): 46-54.

[2]ZHOU X, ZHANG R, HO C K. Wireless information and power transfer: Architecture design and rate-energy tradeoff[J]. IEEE Trans Commun, 2013, 61(11): 4754-4767.

[3]LI Q, ZHANG Q, QIN J. Secure relay beamforming for simultaneous wireless information and power transfer in on-regenerative relay networks[J]. IEEE Trans Vehicl Tech, 2014, 63(5): 2462-2467.

[4]NG D W K, LO E S, SCHOBER R. Wireless information and power transfer: Energy efficiency optimization in OFDMA systems[J]. IEEE Trans Wirel Commun， 2013,12(12): 6352-6370.

[5]ZHOU X, ZHANG R, HO C K. Wireless information and power transfer in multiuser OFDM systems[J]. IEEE Trans Wirel Commun, 2014, 13(4): 2282-2294.

[6]HUANG J, LI Q, ZHANG Q, et al. Relay beamforming for amplify-and-forward multi-antenna relay networks with energy harvesting constraint[J]. IEEE Signal Process Lett, 2014, 21(4): 454-458.

[7]NASIR A A, ZHOU X, DURRANI S, et al. Relaying protocols for wireless EH and information processing[J]. IEEE Trans Wirel Commun, 2013, 12(7): 3622-3636.

[8]HUANG G F, TU W Q, TANG D. Optimal resource allocation in OFDM decode-and-forward relay systems with SWIET[C]∥PIMRC, 2015: 762-767.

[9]HUANG G F, ZHANG Q, QIN J. Optimal joint time switching and power allocation for multicarrier decode-and-forward relay networks with SWIPT[J].IEEE Signal Process Lett，2015, 22(12): 2284-2288.

[10]DINKELBACH W. On nonlinear fractional programming[J]. Manag Sci, 1967, 13 (7): 492-498.

[11]YUILLE A. The concave-convex procedure[J]. Adv Neural Inform Process Syst, 2003, 15(4):915-936.

[12]ZHANG W, MITRA U, CHIANG M. Optimization of amplify-and-forward multicarrier two-hop transmission[J]. IEEE Trans Commun, 2011, 59(5): 1434-1445.

【责任编辑： 陈钢】

Study on Simultaneous Wireless Information and Energy Transfer optimization algorithm in OFDM amplify-and-forward relay systems

HUANG Gao-fei, ZHENG Hui, ZHAO Sai, TANG Dong

(School of Electronic & Information Engineering, Guangzhou University, Guangzhou 510006, China)

Simultaneous Wireless Information and Energy Transfer (SWIET) is an efficient technique to solve the energy-constrained problem in wireless communication networks. In this paper, the Simultaneous Information and Energy Transfer in an OFDM amplify-and-forward relay network with an energy-constrained relay is investigated. The goal is to improve the system end-to-end transmission rate and extend the lifetime of the relay’s battery. Firstly, the optimal energy transfer policy and subcarrier pairing scheme is studied. Then, the power allocation of information transmission and energy transfer time ratio optimization problem is formulated as a non-convex problem, where the objective function and the energy-harvesting constraint are both non-convex. By solving the non-convex problem with fractional programming technique and CCCP (Constrained Concave Convex Procedure) method, the resource allocation optimization algorithm is provided. The simulation results show that our proposed resource allocation scheme can significantly improve the rate performance of SWIET-based OFDM relay networks, compared with the existing resource allocation schemes.

Simultaneous Information and Energy Transfer; Orthogonal Frequency Division Multiplexing (OFDM); relay; resource allocation; fractional programming

2016-06-02;

2016-06-12

黄高飞(1978-),男，讲师，博士.E-mail：huanggaofei@gzhu.edu.cn.

1671- 4229(2016)04-0061-06

TP 391.9

A