学生在解决几何证明题中的深度体验
谢莎
(四川省成都市第十二中学)
学生在解决几何证明题中的深度体验
谢莎
(四川省成都市第十二中学)
一、教学中的两次重创
学习完全等三角形的性质和判定,我决定补充几何证明中添加常见辅助线的方法,结合刚学的三角形的三条重要线段,我把有关中点问题采用的“倍长中线法”放到首位。于是,我选了下面的例题:
例1.已知:如图1,在△ABC中,AB≠AC,D、E在BC上,且DE=EC,过D作DF交AE于点F,DF=AC。求证:AE平分∠BAC
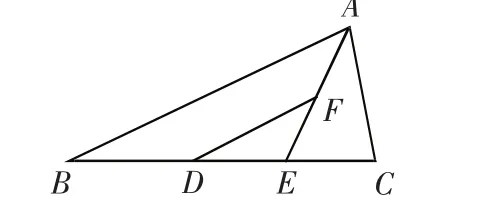
图1
方法1:倍长AE至G,连结DG
方法2:倍长FE至H,连结CH
我激情昂扬地讲解了此题的解法,90%的学生在课堂上的解答良好,令我比较满意。
于是我布置了如下的变式题加以巩固。
【练习】:已知,如图2,在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE
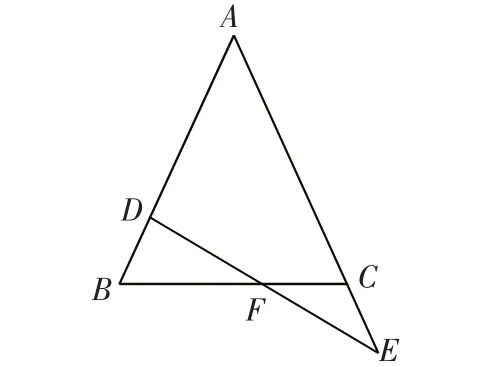
图2
让我意想不到的是全班仅有20%的学生解答正确,我受到了重创。
究竟是哪个环节出了问题?我苦苦思索。
每周二的定时练习如期进行,第九周的数学周考附加题最后一道题是有关“全等三角形的综合证明题”,满分12分,全班38人仅2人全对,得5分的12人,其余均在5分以下,包括2人零分。我更加不明白的是此题所用到的知识点和添加辅助线的方法之前已训练过,为什么学生的掌握情况会这么差呢?完全就像老师在课堂教学中从来未曾涉及过一样,我又受到重创。
二、教学中的尝试
(一)归类训练
1.双等边三角形模型
例2.(1)如图3,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;
(2)如图4,△OAB固定不动,保持△OCD的形状和大小不变,将△OCD绕着点O旋转(△OAB和ΔOCD不能重叠),求∠AEB的大小。
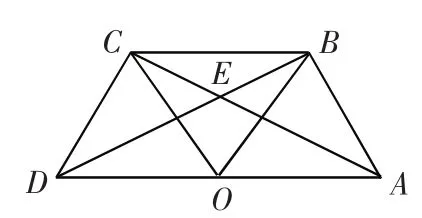
图3

图4
例3.如图5,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,求证:CD=BE,△AMN是等边三角形。
(1)当把△ADE绕点旋转到图6的位置时,是否仍然成立?若成立,请证明;若不成立,请说明理由。
(2)当△ADE绕点A旋转到图7的位置时,△AMN是否还是等边三角形?若是,请给出证明,若不是,请说明理由。

图5

图6

图7
2.垂直模型
例4.如图8,已知△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在A、E的异侧,BD⊥AE于D,CE⊥AE于E。
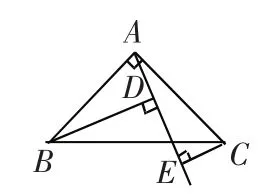
图8

图10

图9
(1)试说明:BD=DE+CE.
(2)若直线AE绕A点旋转到图9位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?写结论,并说明理由。
(3)若直线AE绕A点旋转到图10位置时(BD>CE),其余条件不变,问BD与DE、CE的关系如何?写出结论,可不说明理由。
解决此类题时,我刻意让学生从试题结构上寻找它们的相同点和不同点,在解题策略上寻求异同,从而进行关联体验。但要让学生进行深度体验,还得在试题的变式和迁移上下功夫。
(二)迁移训练
在解决有关线段和差问题,我刻意训练他们添加辅助线的技巧——“截长补短法”。我首先选择难度不大的题作为基架,待他们熟悉此法后,便一步步增加小问题,改变试题的难度,让学生尝试解决。开始之初学生仍具有较大困难,随着训练的深入,添加辅助线完全没有问题,但在逻辑严谨性上存在一些漏洞,这说明学生的深度体验还不够。于是,我又在同类题中适当变式后再训练,多次以后,90%学生能够达到预期目标。
(三)教学体会
1.学生的深度体验需要环境,是步步深入的,多次反复的一个过程;
2.教学目标的实现是在多重因素的相互交织,相互促进的过程中完成的;
3.迁移训练应寻找新旧知识之间的共同因素,注意并重视共同因数的作用,促进正迁移。
4.注意知识整合教学,使之条理化,系统化。
在收获教学的初步成果后,我感觉到课堂教学中核心问题的确定非常重要,它不仅指导学生明确任务,朝着既定方向发展,而且能在任务的指引下进行有效的关联体验,从而促进学生的学习内需,调动学习积极性。此外,教师在教学中要注重基础知识的运用,选择正确的教法,帮助学生对于基本原理的理解,让学生达到越来越高的概括程度,提高认知结构的可利用性。同时,加强发散性思维训练,促进解题的求异能力,提高认知结构的可辨别性,设计数学题组,一题多解、一题多变,巩固知识结构,进而提高认知结构的稳定性。总之,学校的教育科研让我的教学方法上了一个高度,我善于站在不同角度思考问题,善于创新,寻求解决问题的最佳方法。教师的善“变”能促进学生的会“变”,学生在几何问题的解决策略上只有进行深度体验,才能达成解题能力的提升。一系列的变革和训练以后,我对几何教学有了更深的感悟。接下来的教学,我还要寻求更能适合学生体验的问题作为探究方向,不断追求教学的优化点和更高境界,让学生真正有收获。
·编辑薄跃华

