燃气作动筒驱动的弹翼旋转展开过程动力学分析计算
杨侃,雷龙
(中国航天科工集团第六研究院210所,陕西西安710065)
燃气作动筒驱动的弹翼旋转展开过程动力学分析计算
杨侃,雷龙
(中国航天科工集团第六研究院210所,陕西西安710065)
介绍了燃气作动筒驱动的弹翼旋转展开机构动力学分析过程和计算方法,详细分析了各组成单元的工作特性、工作机理、运动和承力特性,综合运用内弹道方程、火药燃速计算公式、火药气小孔射流计算公式、气体状态方程等,推导出了适宜于本系统参数计算的解析公式,并据此编制了计算程序。
燃气作动筒;翼面;计算方法
燃气作动筒推动的弹翼折叠装置展开过程中,由于系统中多个物理过程交织,多种载荷共同作用,解析计算有很大难度,常要通过大量试验来获取需要的数据。为降低成本,提高工作效率,并为相关设计提供具体的参考依据,在对系统进行详尽分析的基础上,建立了相关的计算模型,进而综合利用并改造了内弹道方程、火药燃速计算公式、火药气小孔射流计算公式、气体状态方程及动力学方程,推导出了装置展开过程的解析计算方程组,并推出了相应的数值计算方法。在此基础上用VB语言编制了计算程序,计算出不同状态的特性参数,并以计算结果与试验数据进行了对比验证。

图1 回转式翼面收缩-展开状态图
1 翼面展开机构的概况和翼面气动力计算
本文针对的旋转式弹翼折叠机构基本结构和展开运动过程如附图1所示,折叠/展开机构由回翼面、弹体、燃气作动筒、回转轴等组成,其中燃气作动筒结构如图5所示。可针对在箱式/筒式发射装置内采用本方式折叠翼面的火箭、导弹、无人机等飞行器发射过程的分析计算。发射时,飞行器离开发射箱(筒、架)后,燃气作动筒中的预装药点燃,推动活塞杆外伸,进而带动翼面绕回转轴向外旋转,弹翼开始展开过程,并进入工作位置。
上述过程包含燃气作动筒中的火药燃烧、燃气作动筒的前后腔气体膨胀/压缩、后腔泄流孔气流喷出、翼面升力/阻力迅速变化等组成要素,需要对相关过程分别进行分析计算。
展开过程中,翼面受到因高速运动而产生的气动力、燃气作动筒的推动力、机身的约束力和自身的重力。其中气动力又分为与翼面展开运动平面(也是翼面弦长方向)重合的阻力和与此平面垂直的升力,翼面自身重力因与其它力相比量值较小,计算中予以忽略。用数学方法对展开过程进行了模拟分析,并在此基础上编制计算程序,计算出不同状态的特性参数,并以计算结果与试验数据进行了对比验证。
首先,对翼面所承受的气动力进行分析。按资料[1],翼面升力和阻力的计算公式为:

其中:Cy为翼面升力系数;Cx为翼面阻力系数;ρ为空气密度;S为翼面面积;αy为翼面迎角。
为简便计算过程,对上述公式进行了简化,结果如下:

其中k1、k2分别为与迎角对应的计算参数,当迎角确定时,k1、k2也相应成为常数。θ为翼面横截面与机身纵轴线的夹角,θ0为收缩状态下的上述夹角。
2 燃气作动筒的受力分析及翼身摩擦力的处理
下面对翼面展开过程中燃气作动筒和翼面的运动过程和作用力进行分析:
图2为翼面展开过程中燃气作动筒和翼面的运动过程几何要素图。

图2 翼面展开过程中燃气作动筒和翼面的运动过程几何要素图
上图中,Lx为燃气作动筒某一瞬间的全长,A点为作动筒与翼面的结合点,O点为翼面回转中心,B点为作动筒的尾支点。a(OA)、b(OB)均为已知的结构参数,Ft为作动筒的推力。
由上图可得:

燃气作动筒对回转中心产生的推动力矩为:Ft是燃气作动筒的推力。

阻力矩计算:
翼面与机身的连接可简化为如图3所示。

图3 翼面与机身的连接简图
燃气作动筒需要克服的阻力包括气动力导致的摩擦力和翼面的惯性力,而作用予翼面上的气动力可分为升力Fy和阻力Fx.由于飞行器迎角的存在,升力和翼面回转轴的方向并不完全吻合,但在讨论小迎角飞行问题时,上述差异可以忽略。
阻力引起的摩擦力作用在以R2为半径的圆柱体的侧面上,升力引起的摩擦力作用在以R1为半径的环形平面上,设翼面与机身的摩擦系数为f,则气动力在翼面回转轴上产生的摩擦阻力矩为:

3 燃气作动筒中的推进剂燃烧过程计算
为简便分析过程,假定推进剂的形状为空心圆柱形。简图如图4.

图4 燃气作动筒中装药形状简图
空心圆柱形形装药(圆柱体外圆面紧贴燃烧室内壁)燃烧过程中的已燃火药百分比(即形状系数)计算公式为:

上式中:

式中e为已燃去的火药层厚度,其余参数见图4所示。
由文献[2]P46页,密闭容器中火药的燃烧速度存在下述函数关系:

其中:u1为火药燃速常数;P为火药气压力;n为火药燃速指数。
4 燃气作动筒中带泄流小孔的缓冲气室参数计算
燃气作动筒结构简图见图5.
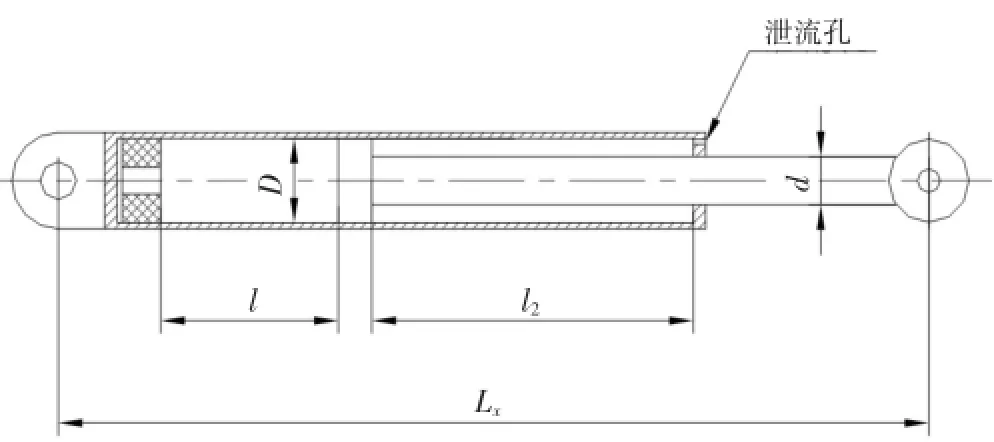
图5 燃气作动筒结构简图
燃气作动筒实际是一个带火药燃烧室的单作用活塞气缸,设置右侧气室是为避免活塞杆伸展到位后出现机械冲击影响飞行器姿态的稳定,右端面上的泄流孔是为调节缓冲气室(即右侧气室)的压力,同时避免发生反弹而设的。
设初始状态下的lx=l0,l20为作动筒右腔的初始长度。
从上述泄流小孔内流出的气体的质量流量为:

假设泄流孔处的气体为理想气体,定常状态,流出速度等于当地音速;认为作动筒缓冲腔中的气体为完全气体,即适用气体状态方程。
文献[3]P242页中提出了一种火炮后效期火炮身管火药气气流逸出流量的计算公式,其推导过程中的基本假设和环境条件与此环境基本类似,这里借用来计算小孔处的气流流动参数:

其中:P0为小孔处的滞止压力,计算时用缓冲腔平均压力取代;R为气体状态常数;T0为小孔处的滞止温度。

上式中k为气体的绝热指数。
由气体状态方程,有:

其中:

代入上式(气体状态方程),得:

式中,S2为作动筒右腔横截面积,l为燃气作动筒活塞行程。
5 用改造的内弹道方程解算燃气作动筒的动力学参数
作动筒左腔是整个系统的动力单元,由火药燃烧产生的高压气体作为动力源。在对火药燃烧过程进行分析之前,先做以下基本假设:
(1)火药燃烧遵循几何燃烧定律;
(2)药粒均在平均压力下燃烧,且遵循燃烧速度定律;
(3)内腔表面热损失用减少火药力f或增加比热比(又称绝热指数)k的方法修正;
(4)用系数φ来考虑其他的次要功;
(5)火药燃气符合诺贝尔-阿贝尔状态方程;
(6)单位质量火药燃烧所放出的能量和生成的燃气的温度均为定值,火药力f、余容α也均认为是常数;
(7)系统不存在泄漏,包括从活塞处发生的内漏。
上述假设下,由文献[3]P78页,过程的动力学状态可以使用内弹道方程来描述。文献[3]中在火药力仅用来推动弹丸沿发射管作直线运动时,标准的内弹道方程为:

其中,S为发射腔横断面面积;P为发射腔压力;f为火药力,f=R·T1;ω为火药总质量;φ为次要功计算系数,常取值1.2;m和u分别为弹丸的质量和速度。
由于本系统中一方面火药力推动的负荷包括作动筒中的活塞+缸杆的直线运动和翼面的回转运动两项(作动筒自身的回转运动影响过小予以忽略),同时运动过程中还存在摩擦阻力。根据上述环境条件,结合对内弹道方程的基本原理的详细分析,本文独创性的提出了存在外部阻力、有多个运动负荷情况下的变形/扩展的内弹道方程:

上式中:m1是作动筒中的活塞+缸杆的质量;J是翼面的转动惯量;lψ是药室容积缩径长度。

式中:V0是药室初始容积;ρp是火药密度;α为火药余容,由火药的成分和密度决定,有如下经验公式:

式中:△为装填密度,△=ω/V0
6 用牛顿定理推导系统的动力学方程
建立系统运动中的动力学方程:
对作动筒:对翼面:


代入(2)、(3)式,有:

以上方程中共有翼面转角θ、燃气作动筒行程l、发射腔压力P、燃气作动筒的推力Ft、缓冲腔压力Ph、已燃火药百分比ψ、已燃去的火药层厚度e七个未知数,联立式(1)、(4)、(5)、(6)、(7)、(8)、(9)共七个方程正可以解出这些未知数。
7 联立方程组推导数值解计算公式
下面对上述方程组的数值法解算做一简单叙述。将(6)、(8)式变形后代入(9)式:
上式与(1)、(7)式连立即可求解θ、l、P三个未知数。
对(1)求导可得:

再求导:

将以上两式代入(10)式,即可得到一关于θ及其导数的方程。用迭代方法即可求得相关参量的数值解。
用上述方法可以在边界条件已知的情况下,计算出翼面展开过程中任一瞬间的展开角度、活塞行程、火药气压力、作动筒后腔压力、作动筒推力、已燃火药量等特征参数,同样,更改任意一个已知的边界条件,例如装药量、火药燃速指数、药柱形状、作动筒直径、活塞开孔直径等,都可以计算出其中任一参数相对其他参数的变化曲线以及对展开过程和展开结果的影响。
利用上述计算方法,采用VB软件编制了计算程序。对某型号的折叠翼导弹弹翼展开过程进行了理论计算,计算过程中先按实际值输入各项边界条件,再给出一个预设的装药量,然后计算弹翼的展开角能否接近90°,如果不能则认为装药量不足,弹翼无法展开。改变装药量再次计算,直到弹翼可以展开,这时的装药量称为临界火药量。改变迎角,得出了不同迎角下的临界火药量,并计算出了各迎角下与临界火药量对应的弹翼的末端速度。计算完成后将计算结果与弹翼展开过程专项试验台的实际试验数值进行了比较,结果两组数据高度吻合,证明这种计算方法是正确和合理的。
[1]李新国.有翼导弹飞行动力学[M].西安:西北工业大学出版社,2005:31-55.
[2]金志明.枪炮内弹道学[M].北京:北京理工大学出版社2004:9-55.
[3]高树滋.火炮反后坐装置设计[M].北京:兵器工业出版社,1995:233-251.
Dynamic Analysis and Calculation of the Dynamic Process of the Elastic Wing of the Gas Actuator
YANG Kan,LEI Long
(China Aerospace Science and Industry Group,Sixth Institute of the 210 Research Institute,Xi'an Shaanxi 710065,China)
This paper introduces the gas as driven by a driving cylinder wing rotary swing mechanism dynamics analysis and calculation method,detailed analysis of the characteristics of each component,working mechanism,motion and force bearing characteristics,comprehensive use of interior ballistic equations,gunpowder combustion speed calculating formula,powder and gas hole flow calculation formula,gas equation of state derived suitable analytical formula to calculate the parameters of the system,and accordingly compile the calculation program.
gas cylinder;wing surface;calculation method
V416.2
A
1672-545X(2016)08-0023-04
2016-05-29
杨侃(1964-),男,陕西西安人,硕士研究生,高级工程师,研究方向为导弹地面设备;雷龙(1980-),男,陕西西安人,本科,工程师,研究方向为地面设备。

