类三角晶格固/固型声子晶体的带隙特性研究*

赵寰宇，曹学勤，宋卫宾，许子龙

(1.北京交通大学 工程力学研究所，北京 100044；2.内蒙古农业大学 理学院，呼和浩特 010018)



类三角晶格固/固型声子晶体的带隙特性研究*

赵寰宇1，曹学勤2，宋卫宾1，许子龙1

(1.北京交通大学 工程力学研究所，北京 100044；2.内蒙古农业大学 理学院，呼和浩特 010018)

首先划分7种类三角晶格声子晶体按三角点阵排列，然后利用平面波展开法计算了类三角晶格钢/环氧声子晶体的反平面模态能带结构，讨论了带隙各向同性和归一化半径对低频带隙的影响。结果表明，类三角晶格钢/环氧声子晶体可以打开不同频率段较宽带隙；选取归一化半径分别为0.34和0.38，使低频带隙得到最大值。这些带隙特征为设计新型减振材料提供了理论依据。

声子晶体；类三角晶格；带隙；归一化半径

0　引　言

对于Bragg散射机理声子晶体，当晶格尺寸至少与弹性波的半个波长大致相当时，就能够产生带隙[3]；而影响带隙的因素主要有填充比、晶格点阵形式、散射体形状、各向异性散射体、弹性模量和质量密度等[1,4-8]。其中晶格点阵形式也是调控带隙频率范围的一个重要因素。对于固-固型声子晶体，Kushwaha等首次计算了镍柱嵌入铝合金基体中形成正方晶格点阵复合结构材料，并获得反平面剪切波带隙[1]。随后，Vasseur等发现碳纤维/环氧和钨/铝周期结构材料都存在完全带隙，结果显示散射体为正方体优于圆柱体产生较宽带隙[4]。旷卫民等研究了二维不同散射体和点阵形式钢/环氧声子晶体的带隙性质，数值计算结果表明正六边形、正方形和正三角形散射体对应三角晶格、正方晶格蜂窝晶格排列能够打开较宽带隙[5]。Lin等研究了各向异性散射体(GaAs,ZnO,Quartz,TiO2)按正方晶格排列于各向同性环氧中组成声子晶体的带隙性质，通过旋转散射体可调节带隙频率范围[6]。赵寰宇等分析了钢/环氧类正方晶格声子晶体的带隙特性，讨论了归一化半径对带隙的影响[7]。另外，不常见复式晶格中的(3.4.6.4)晶格和(34.6)晶格声子晶体的带隙性质还未深入研究，这两种晶格属于二维阿基米德晶格(Archimedean lattices)，它是由正凸多边形组成棋盘状11种类型晶格，采用数学中的Grünbaum-shephard表示方法[9]。

综上所述，本文首先对7种复式晶格—单胞含多个“原子”的类三角晶格的点阵进行划分，然后利用平面波展开法计算了该类型钢/环氧声子晶体的反平面模态能带结构，分析了归一化半径与带隙的关系，讨论了低频带隙分布特征，这些特性对设计新型减振材料具有重要的指导意义。

1　模型的建立

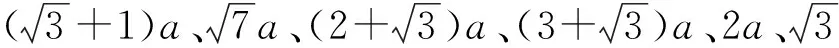
图1　7种类三角晶格声子晶体的示意图及第一布里渊区

为了使用平面波展开法计算弹性波反平面模态声子晶体的能带结构[1]，从弹性波方程入手。在线弹性范围内及无外力作用的情况下，角频率为ω的弹性波在各向异性介质中传播的控制方程为[10]

(1)

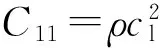
对于二维声子晶体，假设弹性波沿xoy平面传播，波场与z坐标无关，则式(1)可分解为以下两个独立的方程

(2)

(3)

式(2)为平面内混合模态的波动方程，式(3)为反平面剪切模态的波动方程。其中

根据Bloch定理[1,11]，位移矢量u有如下形式

(4)

式中，k为Bloch矢量，G为倒格矢。把式(4)代入(3),可以得到弹性波反平面模态的本征方程[1,11]

(5)

其中矩阵MGG′和NGG′分别是

(6)

(7)

δGG′为Kronecker符号，F(G)为结构函数。采用matlab语言编写程序，可以求解本征方程(5)。然后，让波矢k扫描第一简约布里渊区边界值，可以得到声子晶体能带结构，即其频散曲线。

通过推导复式晶格声子晶体的结构函数，能够容易获取它们的能带结构。以图2为(3.4.6.4)晶格声子晶体截面示意图为例，选取菱形单胞的中心建立直角坐标系，根据结构函数定义和傅立叶平移原理[11-12]，则(3.4.6.4)晶格声子晶体的结构函数为

(8)

其中，散射体中心坐标分别为

J1是一阶贝塞尔函数；填充率

同理，(34.6)晶格、(3.12.12)晶格、(4.6.12)晶格、(3.6.3.6)晶格、(63)晶格和(36)晶格的结构函数和填充率表达式分别为

(9)

(10)

(11)

(12)

(13)

(14)

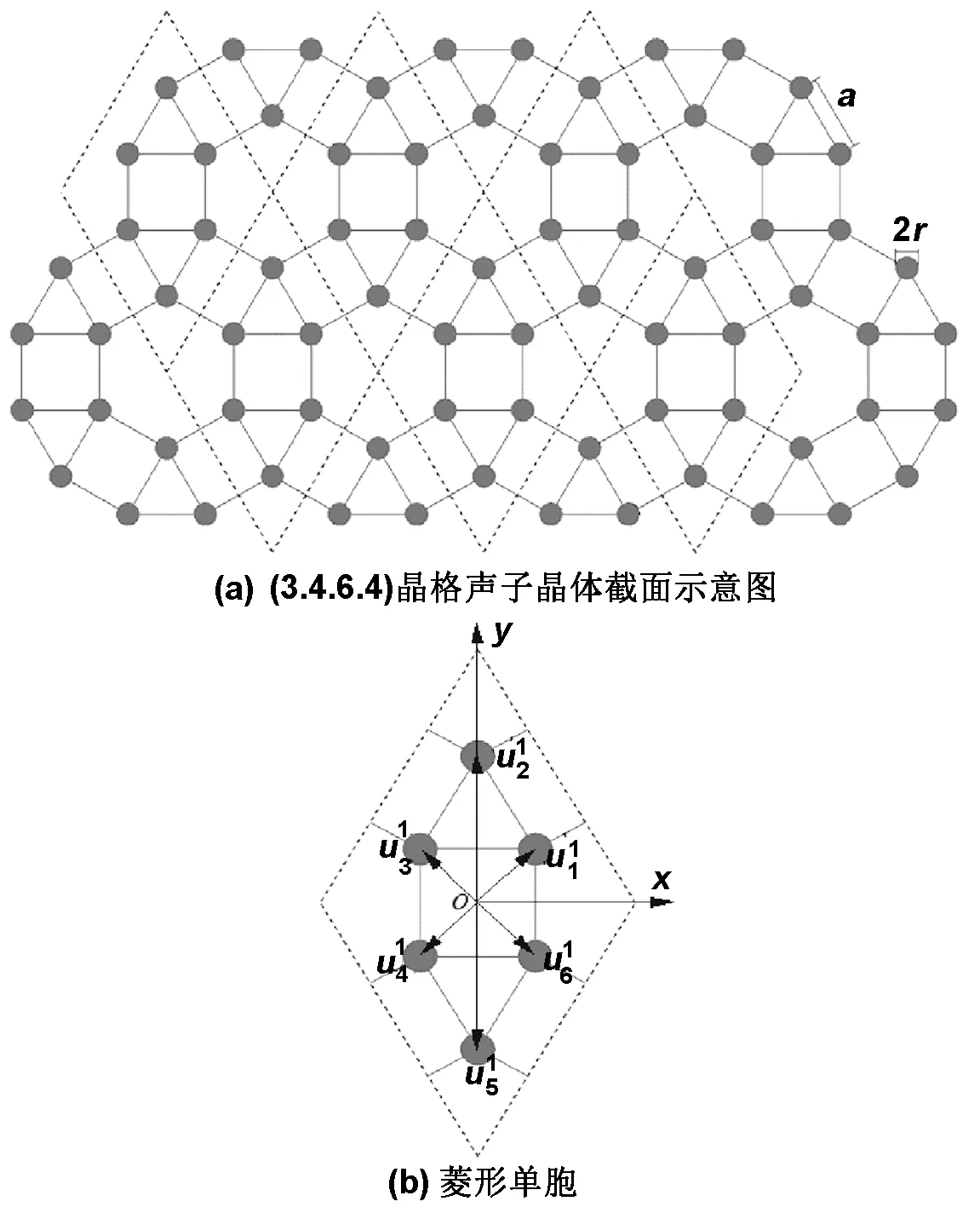
图2　(3.4.6.4)晶格声子晶体截面示意图和菱形单胞

Fig 2(3.4.6.4)lattice structure of phononic crystal and its unit cell of rhombus

2　数值计算与分析

图3给出了归一化半径为r/a=0.34钢/环氧声子晶体的反平面模态能带结构，归一化频率ωa/2πct，其组成材料参数分别为钢的密度和横波波速分别为ρS=7.85×103kg/m3、cSt=3 240 m/s；环氧树脂的密度和横波波速分别为ρE=1.2×103kg/m3、ct=1 160 m/s。

由图3可以看出，单胞均含6个“原子”的(3.4.6.4)晶格、(34.6)晶格声子晶体打开第1和第2带隙带宽近似相等，从第3带隙开始这两种晶体存在多个很宽的带隙，而且这两种晶体的带隙主要在高频段，其填充率值也很高；单胞含6个的(3.12.12)晶格声子晶体有较窄的带隙，填充率值较小；在归一化频率0.8附近，单胞含12个“原子”(4.6.12)晶格声子晶体有多个窄带隙，它的填充率值不大；单胞含3个“原子”的(3.6.3.6)晶格声子晶体从低频到高频产生较宽的带隙，它的填充率较大；单胞含2个“原子”的(63)晶格声子晶体打开低频多个较宽带隙，其填充率值小；单胞含1个“原子”的(36)晶格声子晶体能够产生低频很宽的带隙，其填充率比其它6种晶格都大。所以，使单胞中增加多个“原子”组成复式晶格，可以降低晶体结构对称性，打开更多高频段完全带隙[12]。

在图3中，当弹性波沿着声子晶体的第一布里渊区的ΓM和ΓK两个高对称方向传播时，归一化频率分别为0.7和0.9，(3.4.6.4)晶格和(34.6)晶格钢/环氧声子晶体的第2和第3带隙相对变化均低于0.5%，而(34.6)晶格在归一化频率为0.5的第1带隙相对变化低于0.9%；由此说明：单胞含6个“原子”的类三角晶格钢/环氧声子晶体形成很好的各向同性带隙。在归一化频率为0.5时，(3.6.3.6)晶格钢/环氧声子晶体的带隙表现完美的各向同向带隙。(4.6.12)晶格钢/环氧声子晶体在归一化频率为0.77的带隙相对变化低于1.5%。然而，其它3种晶格声子晶体的带隙各向同性很弱。因此，单胞含6，3和12个“原子”的类三角晶格声子晶体容易产生各向同性带隙，使得各向同性带隙对弹性波传播方向不敏感；该晶体具有类似准晶体性质，带隙带宽仅与相邻“原子”—散射体距离相关[9]。

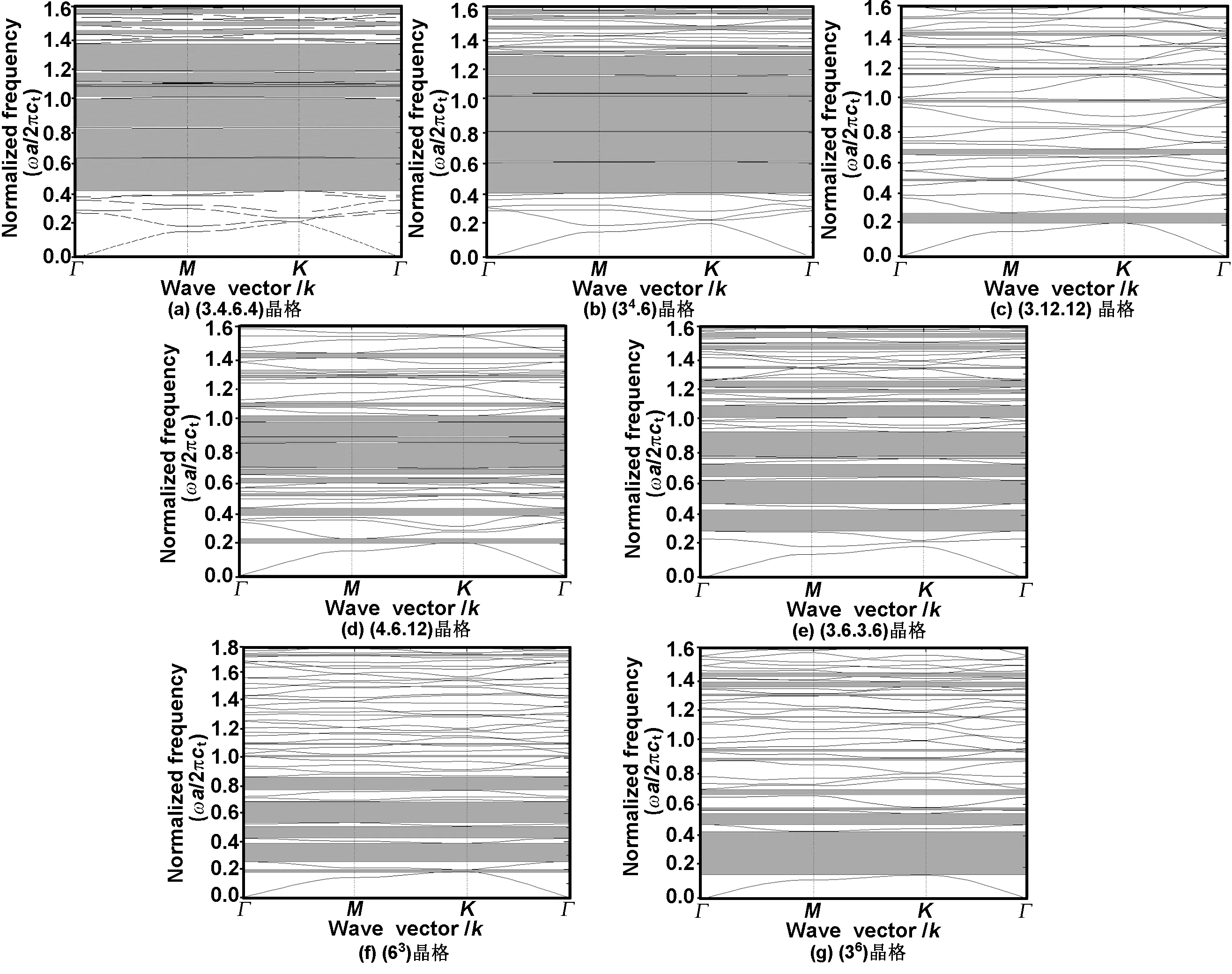
图3　类三角晶格钢/环氧声子晶体能带结构

图4为类三角晶格钢/环氧声子晶体的归一化频率ωa/2πct和归一化半径r/a关系曲线，阴影区域表示带隙频率范围。图4(a)和(b)显示(3.4.6.4)晶格和(34.6)晶格钢/环氧声子晶体的第1，2和3带隙与归一化半径r/a变化趋势几乎一致，带隙的频率范围近似相同，并且它们先增加后减小。

在图4(c)和(d)中，随着归一化半径增大，(3.12.12)晶格和(4.6.12)晶格钢/环氧声子晶体带隙的归一化频率变化规律不显著，趋向于单调增加；与其它晶格比较，这两种晶格声子晶体产生的带隙很窄。

观察图4(e)和(f)发现，随着归一化半径的增大，(3.6.3.6)晶格和(63)晶格钢/环氧声子晶体带隙先增加后减小，(3.6.3.6)晶格从低频到高频都存在多个较宽带隙，(63)晶格很宽带隙主要在低频率段。

图4(g)表明(36)晶格钢/环氧声子晶体的第1带隙带宽明显大于其它6种晶格声子晶体，当归一化半径不断增大，带隙先增大后减小，并向低频方向移动。

由于带隙相对宽度Δω/ωg能够表示声子晶体带隙性质[5]，Δω和ωg分别为带隙带宽和中心频率。图5为类三角晶格钢/环氧声子晶体低频较宽带隙Δω/ωg和归一化半径r/a关系曲线，随着归一化半径不断增加，带隙相对宽先增大后减小。从图中曲线看出，当归一化半径为0.34时，(3.4.6.4)晶格和(34.6)晶格钢/环氧声子晶体的第1带隙相对宽度同时取得最大值，(3.4.6.4)晶格带隙为最宽，并且这两种晶格的带隙相对宽度和归一化半径曲线变化趋势一致，带隙频率非常接近；观察图中A点所标识处，归一化半径为0.34对应(3.4.6.4)晶格、(34.6)晶格、(3.6.3.6)晶格和(63)晶格的带隙相对宽度值大约接近，这表明复式晶体降低晶格点阵对称性[12]，导致了4种晶格类型打开带隙频率范围值相等，而简单晶格点阵不具有这种性质。

图4　类三角晶格钢/环氧声子晶体归一化带隙和归一化半径的关系曲线

Fig 4 Normalized gap width versus the normalized radius for 2D steel-epoxy phononic crystals with triangular-like lattices

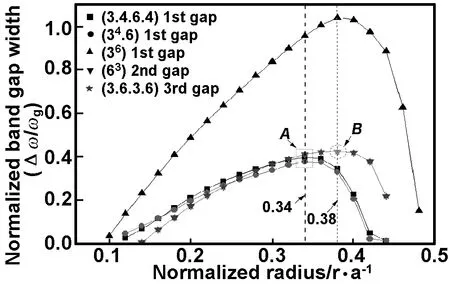
图5类三角晶格钢/环氧声子晶体低频带隙相对宽度和归一化半径的对比曲线

Fig 5 Relative widths of the normalized band gaps for 2D steel-epoxy phononic crystals with triangular-like lattices in lower frequency ranges versus normalized radius

观察图5发现，当归一化半径为0.38时，(36)晶格、(63)晶格和(3.6.3.6)晶格钢/环氧声子晶体相对应的第1，2和3带隙相对宽度均达到最大值；与其它两种晶格比较，(36)晶格获得带隙为最宽；(63)晶格和(3.6.3.6)晶格产生带隙最大值几乎相等，如B点所标识处。因此，单胞含多个“原子”的复式晶格比(63)晶格声子晶体填充率都小，但是它们能够产生很大频率范围较宽带隙，为设计新型减振材料有一定的理论指导作用。

3　结　论

利用平面波展开法研究了反平面模态的类三角晶格钢/环氧声子晶体带隙性质，结论如下：

(1)(3.4.6.4)晶格和(34.6)晶格钢/环氧声子晶体都能够打开高频多个很宽带隙，且第1～3带隙频率范围变化比较接近；(3.12.12)晶格钢/环氧声子晶体存在较窄带隙；(4.6.12)晶格钢/环氧声子晶体只能在归一化频率0.8附近得到宽带隙；(3.6.3.6)晶格钢/环氧声子晶体产生从低频到高频较宽带隙；(63)晶格钢/环氧声子晶体形成低频段较宽带隙；(36)晶格钢/环氧声子晶体的第1带隙为低频段最宽带隙。

(2)单胞含6个“原子”的(3.4.6.4)晶格和(34.6)晶格钢/环氧声子晶体容易产生多个各向同性带隙，其可以使得弹性波传播方向不敏感，具有类准晶体性质。

(3)对于类三角晶格钢/环氧声子晶体，随着归一化半径增大，(3.12.12)晶格和(4.6.12)晶格带隙变化规律不明显，基本趋向增加；其它5种晶格的带隙带宽是先增大后减小。

(4)当归一化半径为0.34时，(3.4.6.4)晶格和(34.6)晶格钢/环氧声子晶体的第1带隙相对宽度均得到最大值，(3.4.6.4)晶格的带隙是最宽；当归一化半径为0.38时，(36)晶格、(63)晶格和(3.6.3.6)晶格钢/环氧声子晶体相对应的第1，2和3带隙相对宽度同时达到最大值，(36)晶格带隙为最宽；(63)晶格和(3.6.3.6)晶格带隙带宽几乎相等。

总的来说，类三角晶格声子晶体填充率相对较小，能够打开多个较宽带隙，可调弹性波传播，这对研究减振材料的波动特性有重要参考意义。

[1]Kushwaha M S,Halevi P,Dobrzynski L,et al.Acoustic band structure of periodic elastic composites [J].Physical Review Letter,1993,71(13):2022-2025.

[2]Liu Zhengyou,Zhang Xixiang,Mao Yiwei,et al.Locally resonant sonic materials[J].Science,2000,289:1734-1436.

[3]Xiao Yong.Locally resonant structures:band gap tuning and properties of vibration and noise reduction [D].Changsha:National University of Defense Technology,2012.

肖勇.局域共振型结构的带隙调控与减振降噪特性研究[D].长沙：国防科学技术大学，2012.

[4]Vasseur J O,Djafari-Rouhani B,Dobrzynski L,et al.Complete acoustic band gaps in periodic fiber reinforced composite material:the carbon/epoxy composite and some metallic systems[J].Journal of Physics:Condensed Matter,1994,6(42):8759-8770.

[5]Kuang Weimin,Hou Zhilin,Liu Youyan.The effects of shapes and symmetries of scatterers on the phononic band gap in 2D phononic crystals[J].Physics Letters A,2004,332(5-6):481-490.

[6]Lin S-C S,Huang T J.Tunable phononic crystals with anisotropic inclusions [J].Physical Review B,2011,83(17):174303.

[7]Zhao Huanyu,Luo Yanhong,Chen Ali.Properties of acoustic band structure of phononic crystal with square-like Archimedean lattices[J].Journal of Synthetic Crystals,2012,41(1):243-247.

赵寰宇,骆岩红,陈阿丽.类正方阿基米德格子声子晶体的声学能带结构特性[J].人工晶体学报,2012,41(1):243-247.

[8]Zhou Xiaozhou,Wang Yuesheng,Zhang Chuanzeng.Effect of material parameters on elastic band gaps of two-dimensional solid phononic crystals[J].Journal of Applied Physics,2009,106(1):014903.

[10]Zhao Huanyu.Characteristic of 2D phonoic crystal with Archimedean lattices [D].Beijing:Beijing University of Technology,2011.

赵寰宇.二维阿基米德格子声子晶体特性研究[D].北京：北京工业大学,2011.

[11]Kushwaha M S,Halevi P,Martinez G,et al.Theory of acoustic band structure of periodic elastic composites [J].Physical Review B,1994,49(4):2313-2322.

[12]Wang Jingli，Chen Heming.Study of complete photonic band gap in two- dimensiona chessboard of non-Bravais lattice [J].Acta Physica Sinica,2007,56(2):922-926.

汪静丽,陈鹤鸣.二维棋盘格子复式晶格的完全光子带隙研究[J].物理学报,2007,56(2):922-926.

Study on band gaps of two-dimensional solid/solid phononic crystals with triangular-like lattices

ZHAO Huanyu1，CAO Xueqin2，SONG Weibin1，XU Zilong1

(1.Institute of Engineering Mechanics,Beijing Jiaotong University,Beijing 100044,China；2.College of Sience Inner Mongolia Agricultural University,Huhhot 010018,China)

In this paper the seven types of two-dimensional triangle-like lattices are classified by simple triangular lattice.The band gaps of antiplane modes for two-dimensional phononic crystals with triangle-like lattices composed of circular steel rods in epoxy are investigated by a plane wave expansion method.The isotropic band gaps and effect of the normalized radius on the band gaps are discussed.The numerical results show that the steel-epoxy phononic crystals with triangle-like lattices can open some the wider band gaps in the large frequency ranges.The maximum values of the band gaps in the lower frequencies are obtained if choosing the normalized radius 0.38 and 0.28.These findings of band gaps would provide the theoretical evidence to design new types of isolated materials.

phononic crystal; triangular-like lattice; band gap; normalized radius

1001-9731(2016)09-09001-06

国家自然科学基金资助项目(11302021)；中央高校基本科研业务费专项资金资助项目(2014JBM097)；北京交通大学人才基金资助项目(2014RC001)；天津市自然科学基金资助项目(15JCQNJC42600)

2015-08-05

2016-01-20 通讯作者：赵寰宇，E-mail:zhaohy@bjtu.edu.cn

赵寰宇(1978-)，男，内蒙古赤峰人，博士，硕导，从事声子晶体、声学超材料的设计和实验研究。

O347；TB533

ADOI:10.3969/j.issn.1001-9731.2016.09.001