波浪加速度不对称性对海床液化的影响

陈俊东，张 弛，隋倜倜，郑金海

（1.河海大学海岸灾害及防护教育部重点实验室，江苏南京 210098；2.河海大学港口海岸与近海工程学院，江苏南京 210098）

波浪加速度不对称性对海床液化的影响

陈俊东1，2，张 弛1，2，隋倜倜1，2，郑金海1，2

（1.河海大学海岸灾害及防护教育部重点实验室，江苏南京 210098；2.河海大学港口海岸与近海工程学院，江苏南京 210098）

为研究加速度不对称波浪作用下的海床响应特征，基于Biot多孔弹性介质理论建立了波浪作用下海床响应数学模型，采用水槽实验数据对模型进行了验证。通过引入加速度不对称波浪压力边界条件的计算方法，模拟分析了波浪加速度不对称性对海床内部孔隙水压力、有效应力以及土体液化的影响。结果表明，波浪加速度不对称性会引起海床表层正向孔压幅值的显著衰减，使孔压的空间分布变得偏斜，减小了液化深度和宽度，使海床液化区域变得窄而浅。

波浪；加速度不对称；海床响应；孔隙水压力；液化

海洋波浪的周期性运动在海床表面产生往复的波压力，会影响海床土体内的有效应力和孔隙水压力的时空变化。在一些不利条件下，可能发生海床表层土体的液化现象，造成海床土体承载能力下降。

国内外许多学者开展了波浪作用下海床响应的研究工作。Madsen等［1-2］借助Biot固结理论和复变量表达式，提出了线性波作用下多孔介质海床动力响应的解析解。Mei等［3］提出了波浪与海床相互作用的边界层近似解法。林缅等［4］基于Yamamoto模型，讨论了线性波条件下波高、周期、相对水深、海床厚度、渗透系数以及饱和度等参数对海床响应的影响。这些研究大多基于线性波理论，并未考虑实际波浪的非线性特征。

Jeng等［5］分析了二阶Stokes波作用下的海床响应，发现当波陡较大和相对水深较小时，波浪非线性对海床响应的影响不可忽略。高福平［6］采用Biot固结理论和有限元法，分析了二阶Stokes波作用下海床动力响应。王忠涛等［7］以广义Biot动力固结理论为基础，对非线性波浪压力作用下饱和砂质海床的动力响应进行了研究，发现与线性波条件相比，一阶椭圆余弦波和二阶Stokes波作用下的孔隙水压力与有效应力幅值显著增大。程永舟等［8］建立了非线性波浪与海床相互作用数学模型，探讨了椭圆余弦波作用下沙质海床孔隙水压力的响应规律。这些研究大多采用某一个特定的非线性波浪理论，反映了波峰压力大于波谷压力这一不对称特征。然而在实际海岸中，非线性波浪往往兼有压力幅值不对称和压力变化加速度不对称的特征，后者会使得波形呈现出一定的“锯齿形”［9］。波浪加速度不对称性无法用已有的波浪理论来描述，其对海床响应的影响仍有待研究。

本文基于Biot多孔弹性介质理论建立了波浪作用下海床响应数学模型，在实测数据验证的基础上，引入加速度不对称波浪压力边界条件的计算方法开展数值模拟，探讨波浪加速度不对称性对海床液化及孔隙水压力、土体有效应力的影响。

1 数学模型

1.1 控制方程

基于Biot理论，考虑弹性可压缩海床的土骨架和孔隙流体，应用Hooke定律描述土骨架应力应变关系，假定海床土体均匀且各向同性，应用Darcy定律描述孔隙流体在海床中的流动，则波浪作用下海床响应可使用以下土体整体平衡方程、孔隙流体平衡方程和质量守恒方程来描述［10］：

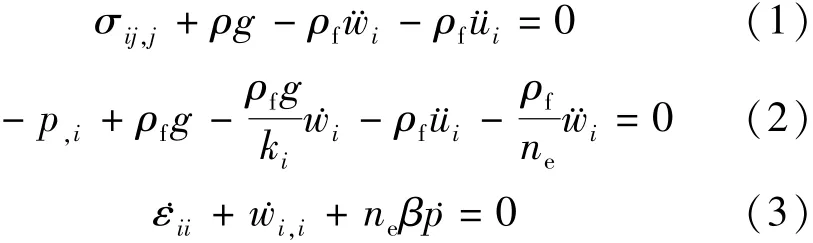
式中：σij为总应力；p为孔隙水压力；ρ为孔隙介质的总密度；ρf为孔隙流体密度；g为重力加速度；ui为土骨架位移；wi为孔隙流体相对于土骨架的平均位移；ki为多孔介质的渗透系数；ne为多孔介质的孔隙率；β为孔隙流体的压缩模量；ε为土骨架应变。

土骨架应变、孔隙流体压缩模量的表达式为式中：Kw为孔隙流体的体积模量；d为水深；Sr为饱和度。

总应力σij与有效应力′和 孔隙水压力p的关系为

式中：δij为Kronecker指标；总应力和有效应力的符号定义为“压为负，拉为正”。

1.2 边界条件

海床的左右侧边界和底边界视为不可渗透的刚性边界，孔隙流体无法通过此边界传递，即土体位移usoil为零、孔隙流体位移uf为零以及孔隙水压力法向梯度为零：

在与波浪交界的海床表面处，给定狄利克雷边界条件，即孔隙水压力p等于当地波浪压力pw。因海床表面的土体应力相比于波浪压力为一很小的量，故在表面边界取土体正应力和切应力等于零：

1.3 数值格式

使用交错矩形网格划分计算域，孔压与物理参数等标量定义在网格中心点，位移和应力等矢量定义在网格单元6个界面的中心点。网格步长在整个计算域中是可变的，在动力过程复杂的区域局部加密网格。采用二阶Crank-Nicolson全隐式有效差分法离散控制方程，采用多向ADI方法求解不同方向的控制方程，采用蛙跳格式求解不同控制方程中的不同物理量，使用欠松弛技术来保证在每个时间步都能得到稳定的迭代解［11］。

1.4 模型验证

已有的波浪作用下海床响应的物理实验主要是在线性波条件下进行的，尚没有单独加速度不对称波浪条件下的实测数据。因此，选用了线性波和椭圆余弦波条件下的两组实验数据来验证模型，从整体上论证非线性波作用下海床响应的模拟精度。

Tsui等［12］在长24.7m、宽0.61m、高0.92m的波浪水槽中测量了线性波作用下的海床内部孔隙水压力变化。实验研究了波高H=0.02m、周期T= 1.5 s、水深d=0.488m、波长L=2.8m、海床厚度h= 0.33m条件下粗沙和细沙两组不同海床的孔隙水压力。数学模型中的参数设置为：孔隙流体的体积模量Kw=1.95GPa，孔隙流体密度ρf=1.00 t/m3，土体密度ρs=2.65 t/m3，孔隙率ne=0.3，弹性模量Ev= 13.333MPa，泊松比ν=0.333，粗沙的渗透系数k=1.0×10-3m/s，饱和度Sr=0.988，细沙的渗透系数k=5.0×10-4m/s，饱和度Sr=0.985。数学模型的计算区域长12m，其中左半部分为细沙海床，右半部分为粗沙海床。模型计算区域长度设置是为了消除侧边界条件对中心区域的影响，设置更长的计算区域对结果没有影响。粗沙和细沙的区别主要体现在渗透系数和饱和度，粗沙的渗透系数和饱和度较大，模型中这两个参数均取实验测量值。海床表面处的波浪压力边界条件由线性波理论计算给定。

Jeng［13］基于固结理论推导出线性波作用下有限厚度、均质海床的孔压分布解析解，这个解析解仅适用于线性波条件，忽略了土体和孔隙流体的加速度效应。图1比较了海床内最大孔压的垂向分布计算结果与Jeng［13］解析解以及Tsui等［12］实验数据，发现相同深度下粗沙最大孔压大于细沙情况下的最大孔压，计算结果与实测数据及解析解吻合良好，最大孔压的量值随渗透系数和饱和度的增大而增大。

卢海斌［14］在长60m、宽1.5m、高1.8m的实验水槽中测量了椭圆余弦波作用下的海床内部孔隙水压力变化。实验条件为：波高H=0.12m、周期T= 2.0 s、水深d=0.30m、波长L=3.35m、海床厚度h= 0.20m。海床的物理参数为：孔隙流体的体积模量Kw=2.00GPa，孔隙流体密度ρf=1.00 t/m3，土体密度ρs=1.90 t/m3，孔隙率ne=0.3893，弹性模量Ev= 26MPa，泊松比ν=0.3，渗透系数k=1.0×10-3m/s，饱和度Sr=0.970。海床表面处的波浪压力边界条件由一阶近似椭圆余弦波理论［7，10］计算给定。

图1 线性波条件下最大孔压垂向分布

图2比较了椭圆余弦波作用下最大孔压垂向分布的模型计算值与实验数据［14］，两者吻合良好，说明模型可以较好地描述非线性波浪作用下的海床响应过程。

图2 椭圆余弦波条件下最大孔压垂向分布

2 加速度不对称波浪作用下的海床响应

2.1 加速度不对称波浪压力边界条件的给定

由于现有的波浪理论还无法描述波浪加速度的不对称性，本文不采用某个特定的波浪理论来计算波浪压力边界条件，而是利用一个经验公式直接给定具有加速度不对称特征的波浪压力场时空分布。Abreu等［9］提出了一个经验公式来描述某一点处的非线性波浪振荡速度时间序列，本文借鉴其做法来描述非线性波压的时间序列，该公式可以同时表征波浪压力以及波浪压力变化加速度的不对称性：

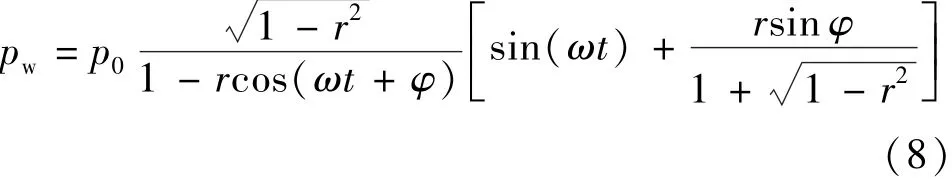
式中：p0为波浪压力幅值；ω为角频率，ω=2π/T，T为周期；φ为波形系数，φ=0代表加速度不对称波形，φ=-π/2代表速度不对称波形；r为加速度不对称系数，0≤r＜1，r=0代表加速度对称，r越大则加速度不对称性越强。本文仅考虑加速度不对称波浪，故取φ=0。图3比较了4个不同r值时的波浪压力时间序列，随着r增大，压力加速度不对称性逐渐明显。

图3 加速度不对称波浪压力时间序列

假定波浪在传播方向上的变形很小，可通过以下关系式得到整个海床面上的波浪压力时空分布：

式中c为波速。由式（9）可以求得某一点处的波浪压力时间序列。

2.2 加速度不对称性对海床响应的影响

选取不同的加速度不对称系数r开展数值计算，研究波浪加速度不对称性对海床响应的影响。参考王栋等［15］的研究案例设置参数，波浪条件：波浪压力幅值p0=13.5 kPa、周期T=7.0 s、水深d= 4.0m、波长L=40m，4个算例分别取r=0、0.25、0.50、0.75；海床参数：厚度h=20m，孔隙流体的体积模量Kw=2.00GPa，孔隙流体密度ρf=1.00 t/m3，土体密度ρs=2.00 t/m3，孔隙率ne=0.3，弹性模量Ev=26.66MPa，泊松比ν=0.333，渗透系数k=5.0× 10-4m/s，饱和度Sr=0.985，海床计算长度为200m。

图4给出了4个算例中最大有效应力绝对值随海床深度的变化。加速度不对称性的影响随海床深度的不同而有所变化：当z/h＞-0.1时，最大有效应力绝对值随r的增大而增大，同时垂向上最大值出现的位置上升；当z/h＜-0.1时，最大有效应力绝对值在r=0～0.50之间变化较小，但r=0.75时呈现出明显的减小。图5给出了4个算例中最大孔隙水压力绝对值随海床深度的变化。在海床表层土体中，加速度不对称性对最大孔压绝对值的影响很小；在海床底层（z/h＜-0.15），最大孔压绝对值随着r的增大而减小。

图6给出了z/h=-0.1处的孔压变化时间序列。可见，波浪加速度不对称性也体现在孔压变化中。随着加速度不对称系数r的增大，正压幅值明显减小，但负压幅值变化不明显，因而最大孔压绝对值变化不明显（与图5一致）。正压幅值减小是因为加速度不对称性越强，海床表面处的波浪压力从零增长到最大正压的时间越短，导致正压没有足够的时间在海床内部充分发展。图7给出了t=4T时，z/h=-0.1平面上的孔压空间分布，孔压空间变化特征与图6相似，正压幅值随r的增大有明显的衰减。

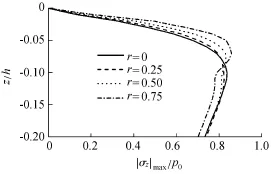
图4 加速度不对称波浪条件下最大有效应力垂向分布

图5 加速度不对称波浪条件下最大孔压垂向分布

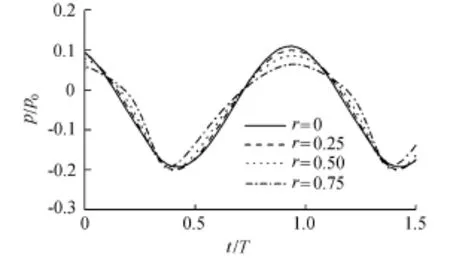
图6 孔压变化时间序列（x=1.5L,z/h=-0.1）

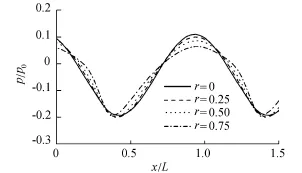
图7 孔压变化空间分布（t=4T,z/h=-0.1）

2.3 加速度不对称性对海床液化的影响

Zen等［16］提出了基于超静孔隙水压力的海床液化判别准则，即当海床内某一点的土骨架重力小于超静孔隙水压力时，其上层海床土体发生液化：

式中：pb为海床表面的波压力；K0为侧压力系数，取为0.5；ρs为土体密度；ρw为水的密度。

图8给出了t=4T时4个算例中海床液化区的分界线，在45～65m之间有一个完整的液化区域。当加速度不对称系数r增大时，最大液化深度变小。液化宽度从海床表面往下逐渐减小，随着r的增大，液化宽度在垂向上有减小更快的趋势。总体而言，波浪加速度不对称性会使海床液化区域变得窄而浅。

图8 海床内液化区域分布（t=4T）

图9 p-pb的空间分布（t=4T,z=-1.9m）

相比于线性波，波浪加速度不对称性导致海床液化区域变得窄而浅，海床土体破坏范围变小，减轻了海工结构物基础承载力的下降程度，对于结构物稳定性是有利的。

3 结 论

a.波浪加速度不对称性的增强会增大表层土体的最大有效应力绝对值，减小底层土体的最大孔隙水压力绝对值，孔压的时空变化也呈现出明显的加速度不对称性。

b.当加速度不对称系数r增大时，海床表层的正向孔压幅值显著衰减，引起相应的超静孔隙水压力减小，使得最大液化深度变小。

c.加速度不对称系数r的增大会引起正压幅值附近的孔压空间分布变得偏斜，液化宽度在垂向上有更快减小的趋势。

d.波浪加速度不对称性通过引起孔隙水压力的空间再分布，使得海床液化区域变得窄而浅。

［1］MADSEN O S.Wave-induced pore pressure and effective stresses in a porous bed［J］.Geotechnique，1978，28（4）：377-393.

［2］YAMAMOTO T，KONINGH L，SELLMEIHERH，etal.On the response of a poro-elastic bed to water waves［J］. Journal of Fluid Mechanism，1978，87（1）：193-206.

［3］MEICC，FODA M A.Wave-induced responses in a fluidfilled poro-elastic solid with a free surface：a boundary layer theory［J］.Geophysical Journal of the Royal Astronomical Society，1981，66：597-631.

［4］林缅，李家春.波浪、海洋土参数对海床稳定性影响［J］.应用数学和力学，2001，22（8）：806-816.（LIN Mian，LI Jiachun.Effects of surface waves and marine soil parameters on seabed stability［J］.Applied Mathematics and Mechanics，2001，22（8）：806-816.（in Chinese））

［5］JENG D S，LIN Y S.Non-linear wave-induced response of porous seabed：a finite element analysis［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1997，21（1）：15-42.

［6］高福平.有限厚度非均质海床对非线性波浪响应的有限元模拟［J］.中国造船，2003，44（增刊1）：447-452.（GAO Fuping.FEM simulation of response of nonhomogeneous sandy seabed of finite thickness to non-linear ocean wave loading［J］.Shipbuilding of China，2003，44（Sup1）：447-452.（in Chinese））

［7］王忠涛，栾茂田，刘占阁，等.浅水区波浪非线性效应对

砂质海床动力响应的影响［J］.海洋工程，2005，23（1）：41-46.（WANG Zhongtao，LUAN Maotian，LIU Zhange，et al.Studies on the effect of non-linear wave loading in shallow water region on dynamic response of sandy seabed［J］.The Ocean Engineering，2005，23（1）：41-46.（in Chinese））

［8］程永舟，王永学，蒋昌波.浅水非线性波作用下沙质底床孔隙水压力响应数值分析［J］.海洋工程，2008，26（2）：63-68.（CHENG Yongzhou，WANG Yongxue，JIANG Changbo.Numericalanalysis of porewater pressure response in sandy seabed under nonlinear wave in shallow water［J］.The Ocean Engineering，2008，26（2）：63-68.（in Chinese））

［9］ABREU T，SILVA P A，SANCHO F，et al.Analytical approximate wave form for asymmetric waves［J］.Coastal Engineering，2010，57：656-667.

［10］王忠涛.随机和非线性波浪作用下海床动力响应和液化分析［D］.大连：大连理工大学，2002.

［11］SUI T，ZHANG C，GUO Y，et al.Three-dimensional numericalmodel for wave-induced seabed response around mono-pile［J］.Ships and Offshore Structures，2015，doi：10.1080/17445302.2015.1051312.

［12］TSUI Y，HELFRICH S.Wave-induced pore pressures in submerged sand layer［J］.Journal of Geotechnical Engineering，1983，109（4）：603-617.

［13］JENG D S.Porous model for wave-seabed-structure interaction：PORO-WSSI（version I）［R］.Dundee：University of Dundee，2010.

［14］卢海斌.波浪作用下沙质海床孔隙水压力的研究［D］.长沙：长沙理工大学，2005.

［15］王栋，栾茂田，郭莹.波浪作用下海床动力反应有限元数值模拟与液化分析［J］.大连理工大学学报，2001，41（2）：216-222.（WANG Dong，LUAN Maotian，Guo Ying. FEM-based numerical Simulation of dynamic response and liquefaction analysis of seabed under wave-induced loading［J］.Journal of Dalian University of Technology，2001，41（2）：216-222.（in Chinese））

［16］ZEN K，YAMAZAKI H.Wave-induced liquefaction in a permeable seabed［R］.Nagase Yokosuka：Port and Harbour Research Institute，1993，31：155-192.

Effects of wave acceleration asymmetry on seabed liquefaction

CHEN Jundong1，2，ZHANG Chi1，2，SUITiti1，2，ZHENG Jinhai1，2（1.Key Laboratory of Coastal Disaster and Defence
（Hohai University），Ministry of Education，Nanjing 210098，China；2.College ofHarbor，Coastal and Offshore Engineering，Hohai University，Nanjing 210098，China）

In order to study the influence ofwave acceleration asymmetry on seabed response，a numericalmodel ofwaveinduced seabed response was developed based on the Biot theory of poroelasticity，and themodelwas validated against the measured data from flume experiments.A method of calculating wave pressure boundary conditions on the seabed surface，which considers wave acceleration asymmetry，is introduced.Effects of wave acceleration asymmetry on pore water pressures，effective stresses，and soil liquefaction of the seabed are discussed based on numerical simulation.Results show thatwave acceleration asymmetry considerably reduces the peak value of the positive porewater pressure in the surface soil layer of the seabed，modifies the spatial distribution pattern of the porewater pressure，and eventually leads to decreases in both the depth and width of seabed liquefaction.

wave；acceleration asymmetry；seabed response；pore water pressure；liquefaction

TV139.2

A

1006-7647（2016）04-0020-05

10.3880/j.issn.1006-7647.2016.04.004

2015- 07 01 编辑：熊水斌）

国家自然科学基金（51209082，51209083）；江苏省普通高校研究生科研创新计划（#CXLX11_0450）

陈俊东（1989—），男，硕士研究生，主要从事海洋岩土研究。E-mail：chenjundong1989@126.com

张弛（1985—），男，副教授，博士，主要从事河口海岸动力学研究。E-mail：zhangchi@hhu.edu.cn