做模拟高考试题中压轴填空题的心得——追根溯源在课本

全志淼（湖南省衡阳市第一中学，湖南衡阳421000）

做模拟高考试题中压轴填空题的心得
——追根溯源在课本

全志淼（湖南省衡阳市第一中学，湖南衡阳421000）

1　实例再现

下面是一次模拟考试试卷中的填空题第16题：

注：此题作为填空题的压轴题，考查了基本不等式、不等式的性质、二元代数式等基础知识；考查抽象概括能力、推理论证能力、运算求解能力等基本能力；考查常值代换的解题方法和转化与化归、特殊与一般等数学思想。其实，本题源于课本，由课本的例题（习题）一步一步演化延伸拓展而来。

2　逐步演变

（1）原型简约，体现三基（人教A版选修4-5［不等式选讲］第35页例题3：）。

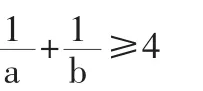
分析：本题结构简单，解法较多。非常典型，能考查同学们的基本知识、基本方法和基本技能。较为简单的方法是常值代换，即：将不等式中的“1”换成“a+b”，或将左边乘以“a+b”，过程如下：

本题也可用直接通分后用基本不等式法，还有消元法、三角换元法、柯西不等式法等等。

（2）改变系数，雏形初现

分析：由于条件“a+2b=1”中的常数还是“1”，当然可采用原型题的解法。

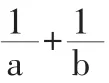
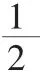
（3）变换结构，提升思维

分析：此次演变，对同学们的分析能力、洞察能力要求较高，难度较大。需要采用常值代换和整体代换的方法解题，即要发现两个分母的关系：（x+3y）+（x-y）=2（x+y）=4。这是建立在对式子结构分析的基础上才能发现的，也是解决本题的关键。后面的解题过程就好办了：

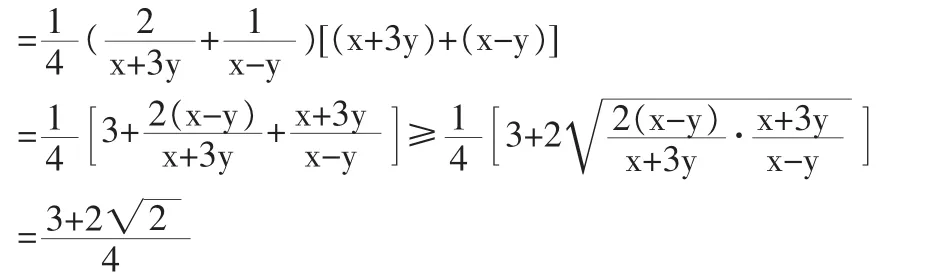
（4）变式不等，压轴成型

分析：经过本次变换，即为开篇所举的模拟考题，条件变为了不等式，同时因为结构的繁琐，在理解上增加了障碍和悬念，有同学会误认为可用“线性规划”来做。也没有了常值代换的背景，极难处理。更有甚者，本题在解题过程中还要运用不等式的传递性。不愧为填空题的压轴题。解法如下：

①拓展延伸

分析：这次的变式，是在模拟题的基础上再进行的变式，难度加大了。显然，（x+4y）+（x-y）=2x+3y，而不再等于（x+y）的多少倍了。这样的拓展，对我们的应变能力及综合能力要求更高。我们如果没有一双“火眼金睛”，是很难发现2x+3y和x+y≤2之间的关系的，这要求我们想到利用待定系数法来配凑系数。还要求能够综合运用基本不等式和不等式的知识，运用常值代换等进行综合解题，对我们的心理承受能力及自信心是极大的挑战，当然，也是我们进行思维训练、培养自信心的大好机会。过程如下：

解：令x+y=λ（x+4y）+μ（x-y），即x+y=（λ+μ）x+（4λ-μ）y

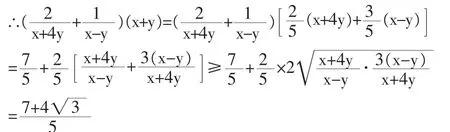
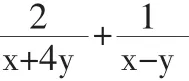
②题后反思

从多套高考数学试题与模拟试题的填空题的压轴题来看，很多题目都源于课本，都能在课本上找到原型。这类题都是以课本题为蓝本，经过变换命题的视角、演变拓展而成，考查与原题有关的基本知识、基本技能，体现了基础性和学好课本知识的重要性，引导我们重视基础、重视教材、研究教材、用好和用活教材。我们在今后的高考复习中，一定要立足课本，回归课本，强化对课本例题习题的研究，不能简单的就题论题，而应进行适当变化、引申、挖掘，揭示其有价值的新结论、新解法，产生触类旁通、举一反三的学习效果，并能开阔思维，发挥一题多用的作用。我们可以有意识地对课本例题习题进行一题多解，一题多变，挖掘出课本例题习题与高考试题的联系，做到“以教材为本”，从而提高高考备考效率。

G634.6

A

2095-2066（2016）26-0259-02

2016-8-30

全志淼（1999-），男，湖南衡阳人，高中。