极限平衡理论下边坡强度参数反演及加固稳定性分析*
邓东平 李 亮
(中南大学土木工程学院 长沙 410075)
极限平衡理论下边坡强度参数反演及加固稳定性分析*
邓东平李亮
(中南大学土木工程学院长沙410075)
参数反演是获得较为可靠的边坡强度参数的一种有效手段。本文在对边坡临界滑动面进行判别的情况下,以瑞典法为基础,通过建立强度参数之间及其与临界滑动面一一对应的关系推导得边坡强度参数反演的显式计算公式。然后,将反演结果用于锚索加固条件下的边坡稳定性研究。经工程算例分析验证了本文方法的可行性和实用性,并得到如下结论:(1)预应力锚索能对边坡形成有效的加固作用,且锚索在坡面上的位置越靠近滑动面的滑出点时其对边坡的稳定性越有利; (2)锚索的预应力越大则计算得到的安全系数越大,而锚索水平倾角的增大对计算得到的安全系数影响微小。
边坡稳定性极限平衡临界滑动面强度参数反演锚索
0 引 言
边坡稳定性是岩土工程中的一个重要研究课题(李宁等, 2010; 杨天鸿等, 2011; 卢坤林等, 2012; 李健等, 2013),而获取准确的土体强度参数是对其进行分析的首要条件(刘明维等, 2009)。一般情况下,确定土体强度参数的方法主要有室内试验、现场原位试验和参数反演(周欣华等, 2000)。对于室内试验,因其所采集的土样大多已被扰动,故土体性质与实际情况差异较大,对于现场原位试验,通常试验成本费用较高,然而,参数反演方法可弥补上述两者的缺点,使之成为获取强度参数的一种有效手段(沈军辉等, 2008; 石崇等, 2010; Zhang et al.,2013; 孙志彬等, 2013)。
在边坡强度参数反演中,获得临界滑动面的位置是进行反演的一个前提。对于临界滑动面的判别,工程上可采用地质勘探来分析边坡内部的软弱界面或通过埋设测斜管来监测边坡的滑动趋势。与此同时,当边坡出现滑动趋势或存在软弱界面时,边坡也存在着较大的不稳定性,需对其进行加固处理以确保稳定性(霍宇翔等, 2009; 韩斌等, 2013),因此,边坡强度参数反演的一个重要目的是为边坡加固设计与稳定性分析提供可靠参数。实际工程中,预应力锚索作为一种有效的手段已被广泛使用(王晓荣等, 2003; 刘才华等, 2006; 李新坡等, 2006; 吴茂明等, 2010; 赵炼恒等, 2013; 邓东平等, 2013),并获得了良好的经济效益,故将强度参数反演结果用于分析锚索加固条件下的边坡稳定性具有重要的工程意义。
本文通过埋设测斜管而得到的监测数据来判断已出现滑动趋势边坡的近似临界圆弧滑动面的位置。同时,以传统的瑞典法为基础获得此临界滑动面上的安全系数与边坡强度参数的简单关系,并由此关系式及强度参数与临界滑动面满足的一一对应关系来反演边坡的强度参数。当采用反演结果时,锚索加固条件下的边坡稳定性被分析,且将其应用于工程算例中,验证了本文方法的可行性,并研究了不同锚索加固型式对边坡稳定性的影响。
1 边坡强度参数反演计算方法

图1 边坡稳定性计算模型Fig. 1 Calculation mode of slope stability

xc=[(ys2-ys1)(ys3-ys1)(ys3-ys2)-
[2(xs1-xs2)(ys3-ys2)-2(xs2-xs3)(ys2-ys1)]
(1a)
yc=[(xs1-xs2)(xs3-xs1)(xs2-xs3)-
[2(xs2-xs3)(ys2-ys1)-2(xs1-xs2)(ys3-ys2)]
(1b)
在求得滑动圆弧的圆心坐标xc和yc后,即可由圆方程计算得圆弧的半径R。由于本文假设边坡的临界滑动面为圆弧,故研究成果更适用于均质边坡岩土强度参数的反演。同时,当实际监测所得滑动面并非表现为圆弧状时,可采用曲线拟合的方法来得到最为合理的近似圆弧滑动面及其相应参数。
如图1b所示,在一般情况下取宽度为dx的微单元土条abcd进行受力分析,作用在其上的力有:重力dW、渗透力dJ、滑动底面剪切力dS和法向力dN。由于在边坡稳定性极限平衡计算方法中,瑞典法(Fellenius, 1936)能够得到边坡安全系数的显式解答,而这一特性有利于边坡的强度参数反演,故采用简单的瑞典法对边坡进行稳定性分析。当采用以土骨架为分析对象时,微单元土条abcd滑动底面上的滑动力dT和抗滑力dR的计算为:
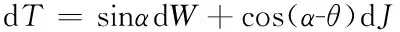
(2a)
(2b)
式中,c为土的黏聚力;φ为土的内摩擦角;α为滑动底面切线的水平倾角;θ为浸润线的水平倾角。
在式(2)中,微单元土条上的重力dW和渗透力dJ的计算式为:
(3a)
dJ=γλ2h1tanθdx
(3b)
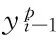
(4a)
(4b)
(4c)

按照瑞典法中边坡安全系数的定义,由式(3)和式(4)可得到边坡的安全系数与抗滑强度参数的关系为:
(5a)
(5b)
(5c)
(5d)
式中,A1和B1分别为边坡滑动面的下、上积分限。
若仍在某段x轴坐标范围(xi-1,xi)内计算式(5)中I1、I2和I3的大小,并将式(4)、sinα=(x-xc)/R和cosα=(yc-yx)/R代入式(5)中,可将I1、I2和I3的计算简化为:
(6a)
(6b)
(6c)
I21=a1(A2+B2)+a2C+a3
(6d)
(6e)
(6f)
(6g)
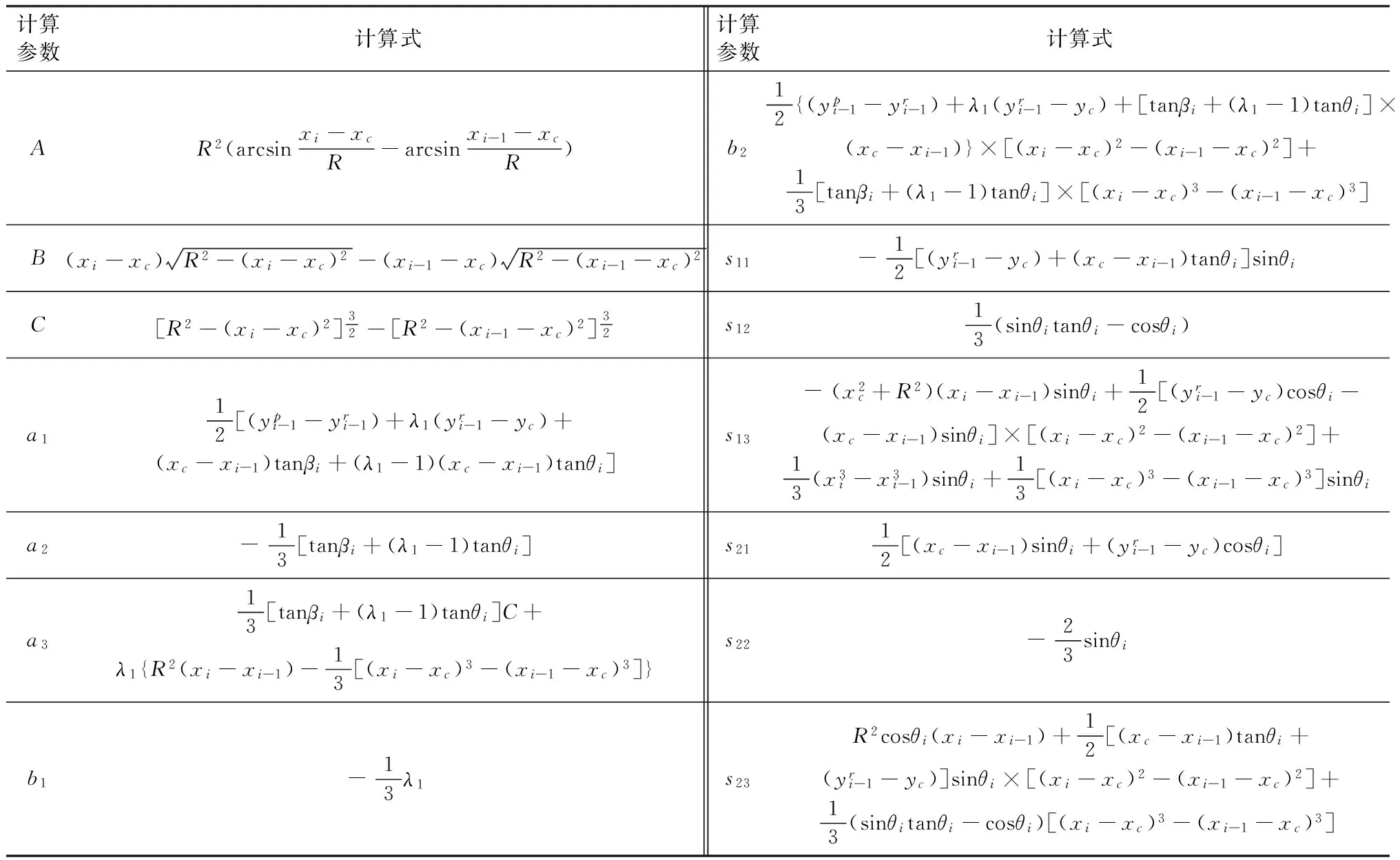
式中,βi和θi的计算如式(4),参数A2、B2、C、a1、a2、a3、b1、b2、s11、s12、s13、s21、s22和s23的计算(表1)。
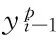
变换式(5a)可得无量纲参数c/(γH)和tanφ与Fs的关系式为:
(7)
表1 参数计算Table1 Calculation parameters
计算参数计算式计算参数计算式AR2(arcsinxi-xcR-arcsinxi-1-xcR)b212{(ypi-1-yri-1)+λ1(yri-1-yc)+[tanβi+(λ1-1)tanθi]×(xc-xi-1)}×[(xi-xc)2-(xi-1-xc)2]+13[tanβi+(λ1-1)tanθi]×[(xi-xc)3-(xi-1-xc)3]B(xi-xc)R2-(xi-xc)2-(xi-1-xc)R2-(xi-1-xc)2s11-12[(yri-1-yc)+(xc-xi-1)tanθi]sinθiC[R2-(xi-xc)2]32-[R2-(xi-1-xc)2]32s1213(sinθitanθi-cosθi)a112[(ypi-1-yri-1)+λ1(yri-1-yc)+(xc-xi-1)tanβi+(λ1-1)(xc-xi-1)tanθi]s13-(x2c+R2)(xi-xi-1)sinθi+12[(yri-1-yc)cosθi-(xc-xi-1)sinθi]×[(xi-xc)2-(xi-1-xc)2]+13(x3i-x3i-1)sinθi+13[(xi-xc)3-(xi-1-xc)3]sinθia2-13[tanβi+(λ1-1)tanθi]s2112[(xc-xi-1)sinθi+(yri-1-yc)cosθi]a313[tanβi+(λ1-1)tanθi]C+λ1{R2(xi-xi-1)-13[(xi-xc)3-(xi-1-xc)3]}s22-23sinθib1-13λ1s23R2cosθi(xi-xi-1)+12[(xc-xi-1)tanθi+(yri-1-yc)]sinθi×[(xi-xc)2-(xi-1-xc)2]+13(sinθitanθi-cosθi)[(xi-xc)3-(xi-1-xc)3]
由式(7)可知,对于给定的临界滑动面且此滑动面上的安全系数Fs已知时(通常情况下,参与边坡强度参数反演的边坡一般已发生滑动或出现滑动趋势,故可认为此临界滑动面上的安全系数Fs=1),存在多个c/(γH)和tanφ组合满足此关系式。然而,在这些组合中仅有一组参数能够使得搜索到的临界滑动面与给定的临界滑动面相同,且此时对应的最小安全系数Fs,min与此给定临界滑动面上的安全系数最为接近,则该组参数即为反演结果。
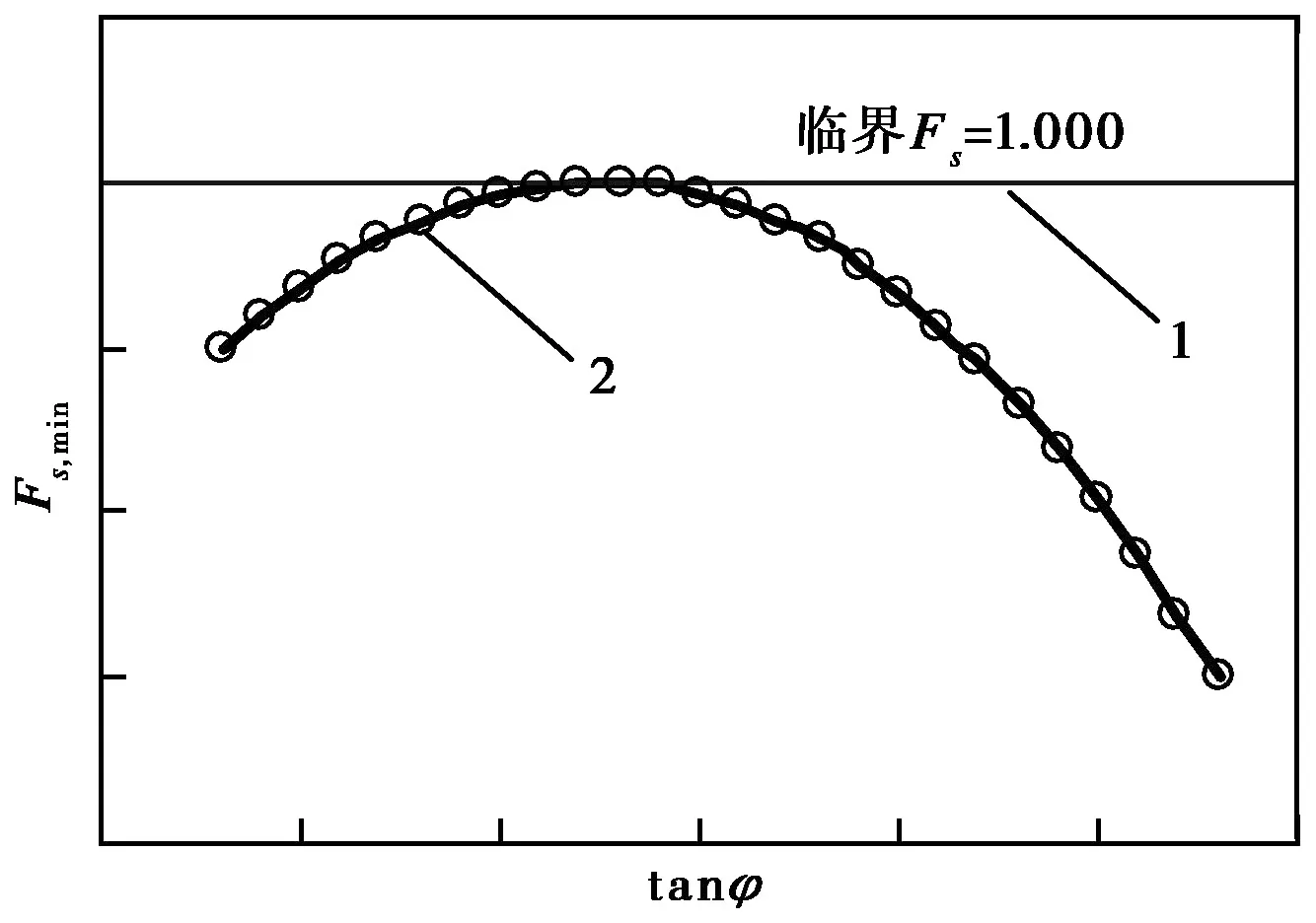
图2 强度参数反演模型Fig. 2 Inversion mode of strength parameters1.临界Fs; 2.边坡稳定性分析Fs曲线
由上述分析可知,以满足式(7)的多个c/(γH)和tanφ组合来采用前述公式对边坡进行稳定性分析时,可得如图2 所示的最小安全系数Fs,min与tanφ的关系曲线,其为一条凸曲线,即当φ为边坡实际的内摩擦角时,由满足式(7)的参数c/(γH)和tanφ组合可使分析所得的边坡稳定性Fs,min最大且最接近于对应给定临界滑动面上已知的安全系数。将Fs,min与tanφ的关系曲线采用如下多项式进行拟合:
(8)
式中,d0、d1、d2和d3为拟合参数,后续算例表明采用此方式拟合的线性相关性R2均大于0.99。
为了求得边坡的实际内摩擦角φ,可在式(8)中令dFs,min/dtanφ=0,然后利用式(7)计算黏聚力c,这样就可通过以判定的临界滑动面及其上已知的安全系数反演得边坡的强度参数。
2 加固条件下边坡稳定性计算方法
采用前述方法对已发生滑动或出现滑动趋势的边坡可反演得到与实际情况相符的抗滑强度参数,而利用这些反演结果来指导边坡的加固具有十分重要的作用,因此,边坡抗滑强度参数反演的一个重要目的是为分析边坡加固措施及加固型式的可行性提供可靠的数据支持。
在众多的边坡加固措施中,预应力锚索因具有较好的加固作用和经济效益故被广泛应用于实际工程,在此利用前述强度参数反演结果来分析锚索加固条件下的边坡稳定性。同时,在前述强度参数反演中简单的瑞典法被采用,然而,在边坡稳定性分析中瑞典法计算所得的结果往往偏于保守而不利于真实反映加固措施对边坡的加固效应,故Morgenstern-Price(M-P)法(Morgenstern et al.,1965)被采用去分析锚索加固条件下的边坡稳定性。
如图3 所示,在预应力锚索加固边坡中,锚索的预应力常作为滑动面上的作用力参与边坡的稳定性分析。当以坡角点为原点建立xy轴坐标系时,滑动面的下、上滑出点分别为A和B,且其对应的坐标分别为(xA,yA)和(xB,yB),若在边坡上布置m排锚索,对于锚索j,其在坡面上的x轴坐标为xj、与滑动面交点的坐标为(xQj,yQj)、水平倾角为δj和单位宽度上的预应力为Qj。在滑动体内任取宽度为bi的土条i(abcd),设锚索j作用在土条i的滑动底面上,土条i滑动底面中点的坐标为(xi,yi)。对土条i进行受力分析,可知土条i上的作用力有如下:重力Wi、锚索预应力Qj、条间两侧法向力Ei-1与Ei、条间两侧剪切力Xi-1与Xi和滑动面底面上的法向力和剪切力Ni与Si。
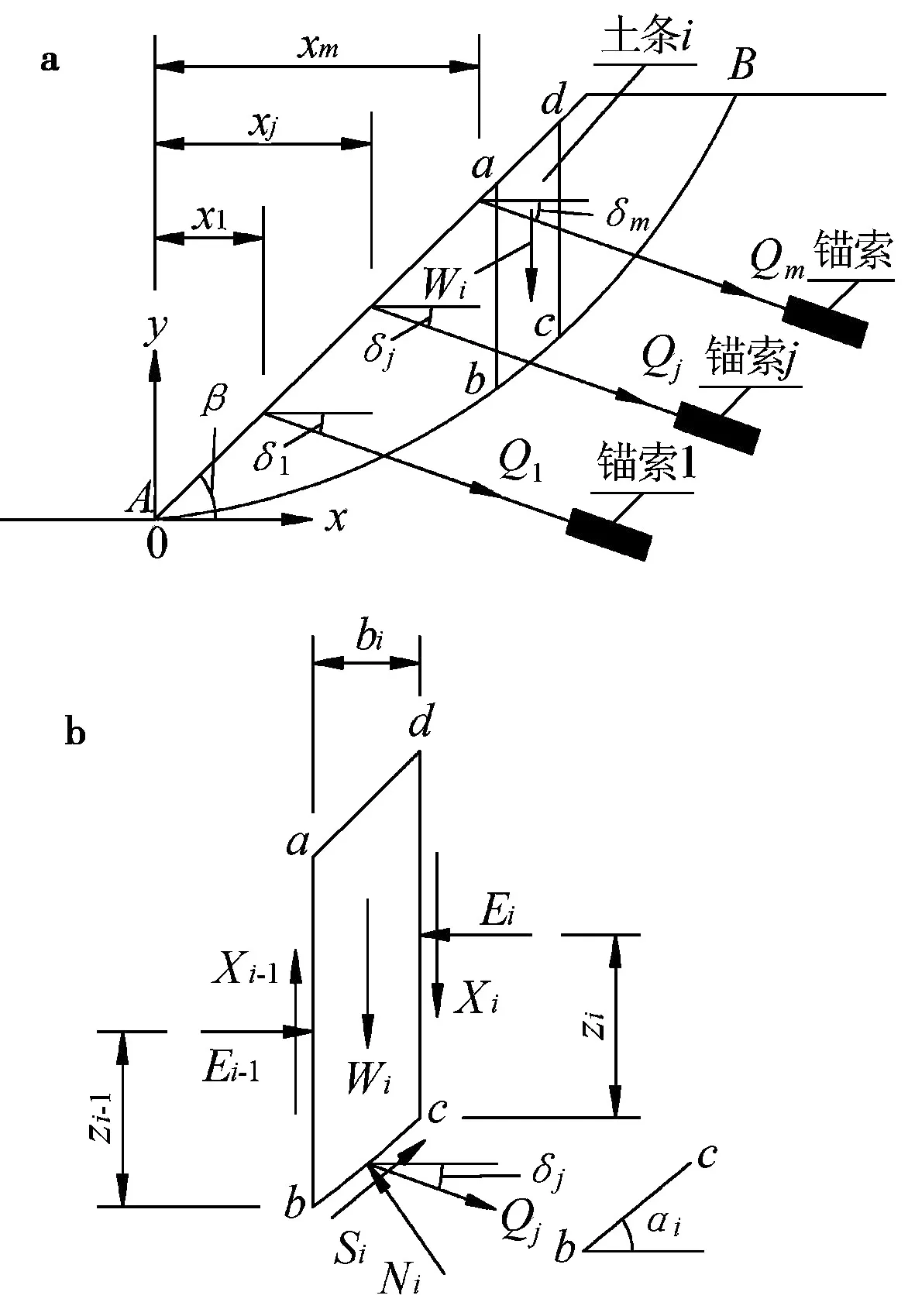
图3 锚索加固条件下边坡稳定性分析模型Fig. 3 Mode for stability analysis of the slope reinforced anchorage cable
在土条i中,由各力沿滑动底面法向和切线方向的力平衡条件可知:
Ni=[Wi+Qjsinδj+(Xi-Xi-1)]cosαi+
[Qjcosδj+(Ei-1-Ei)]sinαi
(9a)
Si=[Wi+Qjsinδj+(Xi-Xi-1)]sinαi-
[Qjcosδj+(Ei-1-Ei)]cosαi
(9b)
式中,αi为土条i滑动底面中点切线的水平倾角。
在M-P法中,条间力Xi和Ei的关系被假设为:
Xi=λfiEi
(10)
式中,λ为计算参数;fi为条间力修正函数;fi=sin[(xi-xA)π](xB-xA)。
由边坡滑动为剪切破坏且服从M-C强度破坏准则,则可得土条i滑动面上的法向力Ni和剪切力Si满足如下关系:
(11)
式中,li为土条i滑动底面的长度,li=bi/cosαi。
将式(10)、式(11)代入式(9)中,便可推导得关于条间法向力Ei的递推公式为:
(12a)
(12b)
(12c)
(12d)
(12e)
(12f)
根据式(12)及端部条件E0=0和En=0,可得边坡的安全系数计算公式为:
(13)
由式(13)即可计算锚索加固条件下边坡的安全系数,下面通过土条上各力的力矩平衡条件来计算参数λ。在土条i中,由各力对滑动底面中点的力矩平衡条件可得:
(14)
式中,zi-1和zi分别为条间两侧法向力Ei-1和Ei作用点位置到滑动底面的竖直距离。
设Mi=Eizi,根据式(14)及端部条件M0=0和Mn=0可得参数λ的计算式为:
(15)
3 工程算例
3.1抗滑强度参数反演与锚索加固边坡稳定性

图4 工程算例Fig. 4 Engineering example

图5 深部位移监测数据Fig. 5 Monitoring data of deep displacement a.测斜管1; b.测斜管2; c.测斜管3
如图4 所示,某高速公路路堑边坡由二级坡段组成(β1=β2=β3=45°),土层材料为碎石土,其天然重度γ=19kN·m-3。施工过程中由于临近边坡的失稳引发该坡段边坡出现了滑动迹象,故在该边坡内从下至上布置3根测斜管来监测边坡的滑动趋势,其中,测斜管1布置在坡脚,测斜管2布置在第一个台阶的平台上和测斜管3布置在第二个台阶的平台上。当以坡角点为原点建立xy轴坐标系时,测斜管1、2和3在x轴上的坐标分别为0m、7m和13m,且埋置深度依次为9m、9m和15m。通过近1a监测所得这3根测斜管累计位移变化曲线如图5 所示。根据累计位移变化量最大来判断滑动位置可知边坡临界滑动面上3个点的坐标分别为s1(0, 0)、s2(7, 3.5)和s3(13, 3.5),单位均为m,同时,由实测数据得出边坡内的地下水位线较低且对边坡的稳定性影响微小。按照前述方法,当假设临界滑动面为圆弧滑动面(滑动圆弧的圆心坐标为xc=-6.5m和yc=29.25m,半径R=29.9635m)时通过反演得到边坡的黏聚力c=3.559kPa和内摩擦角φ=29.375°。
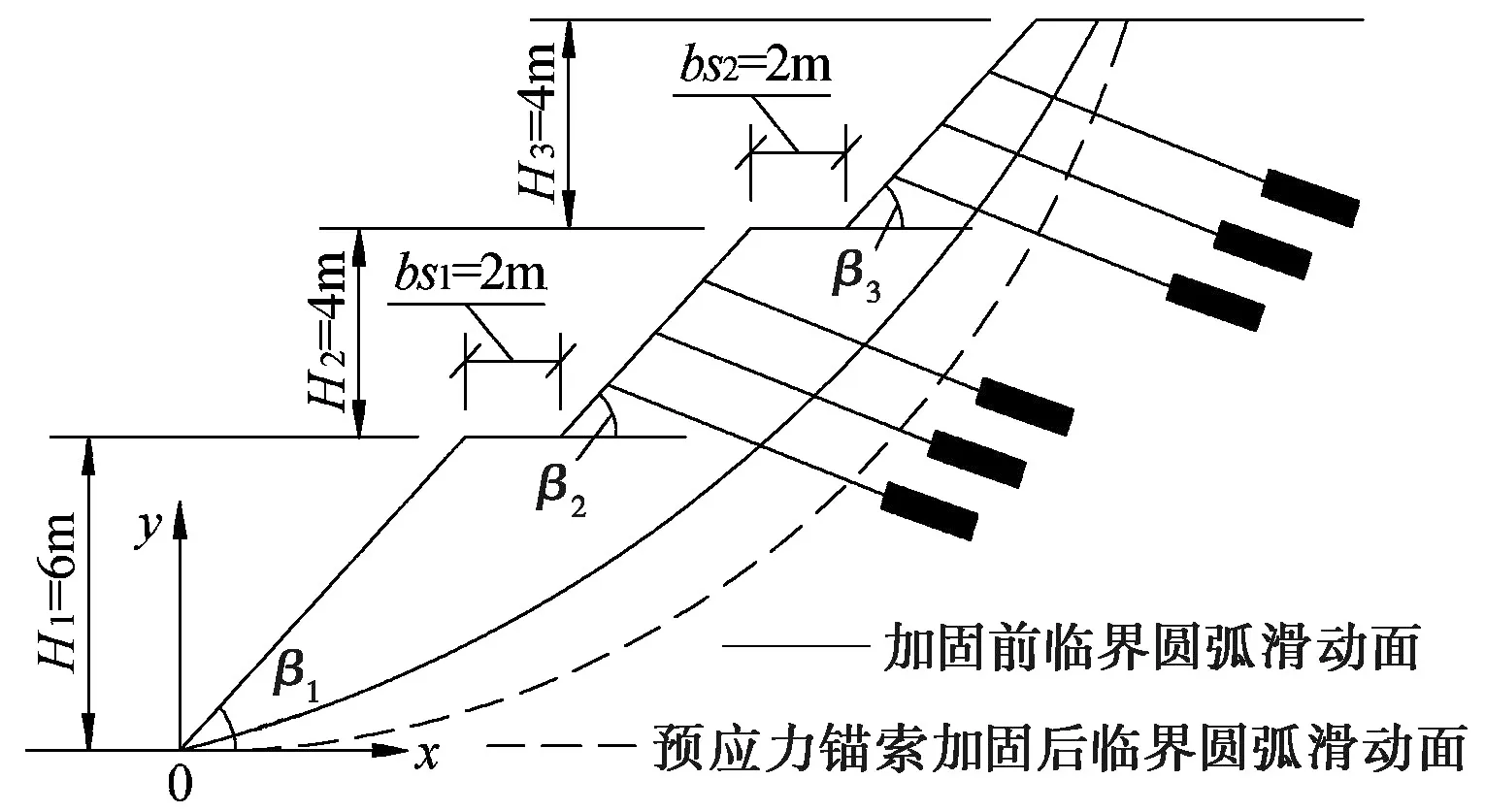
图6 锚索加固布置方式Fig. 6 Arrangement pattern of reinforced anchorage cable
为了确保该坡段边坡的稳定,如图6 所示,对边坡不稳定段采用预应力锚索对其进行加固,加固的方式为:在坡体内由下至上布置6排锚索(其在坡面上的位置分别为x1=9m、x2=10m、x3=11m、x4=15m、x5=16m和x6=17m),锚索的水平倾角均为δ=18°和单位宽度上的预应力均为Q=50kN。由前述反演得的边坡强度参数及锚索加固条件下边坡稳定性计算方法可得该边坡的最小安全系数为1.440,对应的临界圆弧滑动面如图6 所示,由此可知,预应力锚索加固后的边坡安全系数显著提高,且能够确保边坡的稳定性,同时,预应力锚索的作用也使得边坡临界滑动面的范围增大。
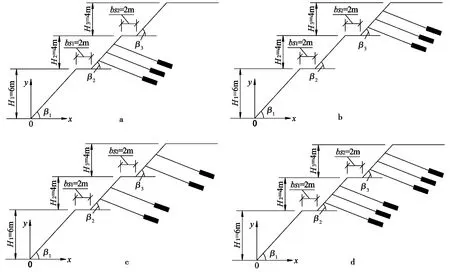
图7 不同锚索加固布置方式Fig. 7 Different arrangement pattern of anchorage cablea.加固方式1; b.加固方式2; c.加固方式3; d.加固方式4
3.2锚索加固型式对边坡稳定性的影响
以下分析不同锚索加固型式对边坡稳定性的影响,如图7 所示,锚索采用如下4种加固方式: ①从下至上布置3排锚索,其在坡面上的位置分别为x1=9m、x2=10m和x3=11m; ②从下至上布置3排锚索,其在坡面上的位置分别为x1=15m、x2=16m和x3=17m; ③从下至上布置4排锚索,其在坡面上的位置分别为x1=9.3m、x2=10.7m、x3=15.3m和x4=16.7m; ④从下至上布置6排锚索,其在坡面上的位置分别为x1=9m、x2=10m、x3=11m、x4=15m、x5=16m和x6=17m。设锚索的水平倾角均为δ及单位宽度上的预应力均为Q。当δ分别为18°、20°、22°、24°和26°及Q分别为40kN、50kN、60kN、70kN和80kN时,各锚索加固方式所得的结果见表2~表5。
表2 锚索加固方式1时不同参数下安全系数对比Table2 Contrast of factor of safety with different parameters in pattern 1 of reinforce anchorage cable

单位宽度上的预应力Q/kN锚索水平倾角δ/(°) 1820222426401.2401.2371.2331.2291.225501.2901.2861.2811.2761.271601.3391.3341.3291.3231.317701.3881.3821.3761.3691.362801.4361.4291.4221.4141.406
表3 锚索加固方式2时不同参数下安全系数对比Table3 Contrast of factor of safety with different parameters in pattern 2 of reinforce anchorage cable

单位宽度上的预应力Q/kN锚索水平倾角δ/(°)1820222426401.1831.1781.1741.1691.163501.2151.2091.2031.1971.191601.2441.2371.2301.2231.215701.2711.2621.2541.2451.237801.2961.2861.2761.2661.256
表4 锚索加固方式3时不同参数下安全系数对比Table4 Contrast of factor of safety with different parameters in pattern 3 of reinforce anchorage cable

单位宽度上的预应力Q/kN锚索水平倾角δ/(°)1820222426401.2671.2621.2561.2501.244501.3201.3131.3061.2991.291601.3691.3611.3531.3441.335701.4171.4081.3981.3881.377801.4621.4511.4401.4281.416
表5 锚索加固方式4时不同参数下安全系数对比Table5 Contrast of factor of safety with different parameters in pattern 4 of reinforce anchorage cable

单位宽度上的预应力Q/kN锚索水平倾角δ/(°)1820222426401.3701.3611.3531.3441.335501.4401.4301.4191.4081.397601.4991.4871.4761.4671.453701.5491.5371.5241.5111.496801.5921.5791.5661.5521.535
从表2~表5中可得:(1)对比锚索加固方式2和方式1所得结果,可知锚索布置方式对边坡的稳定性影响较大,即当锚索在坡面上越靠下布置时(即接近于临界滑动面的滑出点)其对边坡的稳定性越有利; (2)对比锚索加固方式3和方式4,可知当锚索布置的排数较少时可通过增大锚索的预应力来获得相同的边坡稳定性; (3)锚索预应力增大时计算得的安全系数显著增大,而锚索水平倾角增大时计算得的安全系数稍微减小。
4 结 论
基于已知的临界滑动面对处于临界状态的边坡进行强度参数反演,其中,临界滑动面被假定为近似的圆弧滑动面,其参数可通过对预埋测斜管的监测数据进行判别而计算所得,并根据强度参数组合及其与已知临界滑动面的一一对应关系,当采用简单的瑞典法时可推导得边坡强度参数反演的显式计算公式。然后,基于反演结果对预应力锚索加固条件下的边坡稳定性分析,通过工程算例验证,可得到如下结论:
(1)本文边坡强度参数反演方法可行,且计算简单便于工程应用。
(2)预应力锚索可对边坡形成有效的加固作用,且锚索在坡面上布置的位置越靠近滑动面的滑出点时,其对边坡的稳定性越有利。
(3)锚索的预应力越大则计算得到的安全系数越大,而锚索水平倾角的增大对计算得到的安全系数影响微小。
Deng D P,Li L,Luo Q. 2013. Limit equilibrium analysis on stability of soil slopes reinforced with pre-tensioned cables[J]. Journal of Engineering Geology,21(1): 53~60.
Fellenius W. 1936. Calculation of the stability of earth dams[C]∥Proc.2nd Congr. Large Dams. Washington, D.C:[s.n.]: 445~462.
Han B,Zheng L J,Wang S Y,et al. 2013. Synthetic reinforcement of complicated and broken open pit slope[J]. Journal of Central South University(Science and Technology),44(2): 772~777.
Huo Y X,Huang R Q,Ju N P,et al. 2009. Deformation mechanism and stabilization measures of broken granitic rock slope that experienced Wenchuan Earthquake[J]. Journal of Engineering Geology,17(3): 317~321.
Li J,Gao Y T,Wu S C,et al. 2013. Improvement research on the strength reduction method for open pit mines[J]. Journal of University of Science and Technology Beijing,35(8): 971~976.
Li N,Qian Q H. 2010. Four criteria of stability analysis and assessment of high rock slope[J]. Chinese Journal of Rock Mechanics and Engineering,29(9): 1754~1759.
Li X P,He S M,Xu J,et al. 2006. Stability analysis of slopes reinforced with pre-tensioned cables by limit analysis method[J]. Journal of Sichuan University(Engineering Science Edition),38(5): 82~85.
Liu C H,Chen C X,Feng X T. 2006. Discussion on design method of prestressed cable for soil slope[J]. Rock and Soil Mechanics,27(8): 1349~1352.
Liu M W,Zheng Y R,Zhang Y F. 2009. A new inversion method of rock-soils parameters based on complex-variable-differentiation method[J]. Chinese Journal of Computational Mechanics,26(5): 676~683.
Lu K L,Zhu D Y. 2012. The state of the art in the limit equilibrium method by modifying normal stresses over slip surface[J]. Industrial Construction,42(6): 131~136.
Morgenstern N R,Price V E. 1965. The analysis of the stability of general slip surfaces[J]. Géotechnique,15(1): 79~93.
Shen J H,Cui J K,Xu J,et al. 2008. Systematic stress test based back analysis of stress distribution in slope[J]. Journal of Engineering Geology,16(5): 616~619.
Shi C,Zhang Y,Sun H K,et al. 2010. Back analysis of strength parameters of sliding surface of Zhenggang Landslide deposit body[J]. Chinese Journal of Rock Mechanics and Engineering,29(S2): 3728~3734.
Sun Z B,Yang X L,Huang F. 2013. Back analysis of rock slope GSI magnitude under Hoek-Brown criterion[J]. Journal of Central South University(Science and Technology),44(6): 2515~2519.
Wang X R,Jiang Y H. 2003. Application of pre-stressed anchor cable to control engineering of high slope disaster[J]. Chinese Journal of Rock Mechanics and Engineering,22(S2): 2731~2733.
Wu M M,Ruan H T,Liu L. 2010. Application of pre-stressed anchor cables in treatment of geotechnical slopes[J]. Chinese Journal of Geotechnical Engineering,32(S1): 324~326.
Yang T H,Zhang F C,Yu Q L,et al. 2011. Research situation of open-pit mining high and steep slope stability and its developing trend[J]. Rock and Soil Mechanics,32(5): 1437~1451,1472.
Zhang K,Cao P,Bao R. 2013. Rigorous back analysis of shear strength parameters of landslide slip[J]. Transactions of Nonferrous Metals Society of China,23(5): 1459~1464.
Zhao L H,Luo Q,Li L,et al. 2013. Energy analysis method for slopes reinforcing with pre-stressed anchor cables based on minimum energy principle of instability state[J]. Rock and Soil Mechanics,34(2): 426~432.
Zhou X H,Rao X B. 2000. Study on stability of Dayantang Landslide[J]. Journal of Yangtze River Scientific Research Institute,17(2): 41~43,47.
邓东平,李亮,罗强. 2013. 预应力锚索加固土质边坡极限平衡稳定性分析[J]. 工程地质学报,21(1): 53~60.
韩斌,郑禄璟,王少勇,等. 2013. 复杂破碎露天边坡的综合加固技术[J]. 中南大学学报(自然科学版),44(2): 772~777.
霍宇翔,黄润秋,巨能攀,等. 2009. 碎裂结构边坡变形机理及治理对策研究[J]. 工程地质学报,17(3): 317~321.
李健,高永涛,吴顺川,等. 2013. 露天矿边坡强度折减法改进研究[J]. 北京科技大学学报,35(8): 971~976.
李宁,钱七虎. 2010. 岩质高边坡稳定性分析与评价中的四个准则[J]. 岩石力学与工程学报, 29(9): 1754~1759.
李新坡,何思明,徐骏,等. 2006. 预应力锚索加固土质边坡的稳定性极限分析[J]. 四川大学学报(工程科学版),38(5): 82~85.
刘才华,陈从新,冯夏庭. 2006. 土质边坡预应力锚索设计方法探讨[J]. 岩土力学,27(8): 1349~1352.
刘明维,郑颖人,张玉芳. 2009. 一种基于复变量求导法的岩土体抗剪强度参数反演新方法[J]. 计算力学学报,26(5): 676~683.
卢坤林,朱大勇. 2012. 基于滑面正应力修正的极限平衡法的研究现状[J]. 工业建筑,42(6): 131~136.
沈军辉,崔建凯,徐进,等. 2008. 斜坡应力分布的系统测试与反演分析[J]. 工程地质学报,16(5): 616~619.
石崇,张玉,孙怀昆,等. 2010. 争岗滑坡堆积体滑面强度参数反演分析[J]. 岩石力学与工程学报,29(S2): 3728~3734.
孙志彬,杨小礼,黄阜. 2013. Hoek-Brown 准则下岩质边坡的GSI反演[J]. 中南大学学报(自然科学版),44(6): 2515~2519.
王晓荣,蒋育华. 2003. 预应力锚索在高边坡病害治理工程中的应用[J]. 岩石力学与工程学报,22(S2): 2731~2733.
吴茂明,阮含婷,刘鹭. 2010. 预应力锚索在岩土边坡工程治理中的应用[J]. 岩土工程学报,32(S1): 324~326.
杨天鸿,张锋春,于庆磊,等. 2011. 露天矿高陡边坡稳定性研究现状及发展趋势[J]. 岩土力学,32(5): 1437~1451,1472.
赵炼恒,罗强,李亮,等. 2013. 基于失稳状态耗能最小原理的预应力锚索加固边坡稳定性上限解析[J]. 岩土力学,34(2): 426~432.
周欣华,饶锡保. 2000. 大岩淌滑坡稳定性研究[J]. 长江科学院院报,17(2): 41~43,47.
INVERSION OF STRENGTH PARAMETERS AND STABILITY ANALYSIS OF REINFORCED SLOPE WITH LIMIT EQUILIBRIUM THEORY
DENG DongpingLI Liang
(CollegeofCivilEngineering,CentralSouthUniversity,Changsha410075)
Parameter inversion is an effective way to obtain more reliable strength parameters of slope. In the article, after discriminating the position of the critical slip surface, the explicit formulas for inversion of strength parameters are deduced by the established relation between strength parameters and one to one relationship among strength parameters, and the critical slip surface. The classical Swedish slice method is used for calculating the factor of safety. Then, the inversion results are used to study the stability of slope reinforced by anchorage cable. Through analyzing actual case, the feasibility and practicability of the current method are verified. Some conclusion are obtained as follows:(1)Pre-stress cable has an effective reinforcement on slope. Its role on slope stability is more effective when the position of pre-stress cable on slope surface is more near to the lower sliding point of the slip surface; (2)The calculated factor of safety is larger as the pre-stress of cable is larger. Increase of horizontal inclination of anchorage cable has small effect on the calculated factor of safety.
Slope stability, Limit equilibrium, Critical slip surface, Strength parameters, Inversion, Anchorage cable
10.13544/j.cnki.jeg.2016.01.002
2014-12-02;
2015-04-14.
贵州省交通运输厅科技项目(2010-122-020, 2014-122-006)资助.
邓东平(1985-),男,博士后,主要从事道路与铁道工程方面的研究. Email: dengdp851112@126.com
TU41
A

