基于DEM的“两段法”水库塌岸预测研究*
王小东 戴福初② 黄志全
(①华北水利水电大学 郑州 450011) (②北京工业大学 北京 100124)
基于DEM的“两段法”水库塌岸预测研究*
王小东①戴福初①②黄志全①
(①华北水利水电大学郑州450011) (②北京工业大学北京100124)
根据“两段法”进行塌岸预测的基本原理,本文基于Microsoft Visual Studio编程平台和ArcGIS Engine地理信息系统二次开发组件完成“两段法”塌岸预测程序的实现,将“两段法”的应用范围由二维空间拓展到三维空间,实现了塌岸宽度和体积计算的参数化和自动化,通过简单的人机交互,即可完成塌岸预测,提高了塌岸预测效率; 塌岸预测前后岸坡形态的三维可视化对比展示,也为库岸防护工程的实施提供了更可靠的数据支持和决策依据。在程序的实现过程中,塌岸预测参数获取主要通过3个途径:(1)通过野外调查实测数据和室内土工实验结果,获取所需的水下稳定坡角和水上稳定坡角; (2)通过地质图和高分辨率航空影像获取岩性分界线、多年洪水位线、枯水位线等参数信息; (3)基于研究区高分辨率DEM(Digital Elevation DEM)数据,绘制地形剖面线,为程序运行提供终止条件。
DEM两段法水库塌岸ArcGIS Engine
0 引 言
河流在多年的运行中,丰水期水位上涨,枯水期水位下落,逐渐形成较为稳定的河流岸坡,但由于水库的建造,库区地质环境和水文条件较之前发生了前所未有的改变(何良德等, 2007),特别是水库蓄水之后,库岸边坡在风浪和水位变化等因素的作用下,原有的平衡条件被打破,发生坍塌,以各种各样的库岸再造方式,使库岸达到新的平衡状态(阙金声, 2007)。国内外学者针对塌岸研究主要体现在以下两个方面:(1)塌岸范围预测研究。以前苏联学者为代表,其预测方法可以分为两派,一派是以卓洛塔廖夫为代表的条件比拟法; 一派则为康德拉捷夫为代表的数学分析法。采用较多的是卡丘金的计算公式(最终预测)和卓洛塔廖夫的图解法(10a和最终预测)(张倬元等, 1994; 王征亮, 2005; 何良德等, 2007)。在此基础上,国内学者将卡丘金图解法进行拓展,产生了岸坡结构法、两段法等塌岸预测方法(王跃敏等, 2000; 刘天翔, 2006; 许强等, 2007);(2)塌岸机理研究。以Simon为代表的西方学者着重从塌岸发生机理方面进行研究(Millar et al.,1993; Osman et al., 1998; Eddy et al. 1999; Millar, 2000; Wood et al., 2001; Simom et al., 2003)。其中,Simon等基于Excel开发了BSTEM(Bank-Stability and Toe Erosion Model)模型,通过选择剪切面、土层属性、孔隙水压力、水位线、植被状况以及岸坡趾部侵蚀算法等,对岸坡稳定性做出评价(Simon et al.,2003,2007),但剖面线绘制以手动输入点的方式进行,极为不便且难以获取详细的地形剖面线。
王跃敏等(2000)经过近10年对数十处水库塌岸的调查和研究,在卡丘金图解法进行塌岸预测的基础上,提出使用“两段法”来指导外福铁路线的塌岸预测设计,该方法已在外福线水库塌岸预测中得到成功的应用,较适用于我国南方峡谷型水库的塌岸预测(王跃敏等, 2000)。虽然如此,但“两段法”存在明显不足:(1)塌岸预测仍停留在传统的二维塌岸宽度预测之上,对于塌岸的体积预测较少,且定量化程度低; (2)在实际的预测方法实施中,采用二维图解的实现方法,自动化程度低,岸坡预测前后的三维形态信息也未能很好地展示。高分辨率DEM数据的应用和GIS(Geographical Information System,地理信息系统)技术的引入,将使这一现状得到改善。本文采用“两段法”作为塌岸预测的基本方法,结合GIS组件开发技术,应用高分辨率DEM数据,将“两段法”由二维空间拓展到三维空间,由二维塌岸宽度计算拓展到三维塌岸体积计算,并将预测塌岸后岸坡形态以三维可视化的方式进行展现,同时实现了塌岸预测过程的参数化、自动化和可视化。
1 “两段法”的基本原理
“两段法”的基本原理是:预测塌岸线由水下稳定岸坡线和水上稳定岸坡线的连线组成,水上稳定岸坡线的起点,所对应的同高度的原始岸坡点与该线终点之间的水平距离,即为预测的塌岸宽度Sk,如图1a所示。水下稳定岸坡线由原河道多年最高洪水位h及倾角α确定,水上稳定岸坡线由设计洪水位和毛细水上升高度H′及倾角β确定。图1a给出“两段法”的二维图解:以原河道多年最高洪水位与岸坡交点A为起算高程点,以α为倾角绘出水下稳定岸坡线,该线延伸至设计洪水位加毛细水上升高度的高程点B,再以B点为起点,以β角为倾角绘出水上稳定岸坡线,该线与原岸坡的交点C即为水上稳定岸坡的终点。水上稳定岸坡线的起点B的高程所对应的原岸坡点D与该线终点C之间的水平距离,即为“两段法”预测的塌岸宽度Sk(王跃敏等, 2000)。
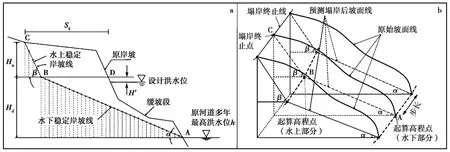
图1 (a)“两段法”的二维图解原理(王跃敏等, 2000); (b)“两段法”的三维图解原理Fig. 1 (a)Two-dimension schematic diagram of Two Section method(Wang et al., 2000); (b)Three-dimension schematic diagram of Two Section method(b)
本文在应用地理信息系统二次开发方法实现塌岸宽度的快速求解的同时,将“两段法”做了新的拓展,即将原来的二维的求解方式拓展到三维的求解方式上来,使得塌岸预测中体积的计算变得简单快捷,同时可以预测塌岸后水库岸坡的三维形态。因此,在塌岸预测实现的过程中,所需要的参数与二维图解法类似,但因应用了高分辨率DEM数据,又有所不同,主要的参数及其获取方式包括:
1.1塌岸剖面线
基于2.5m×2.5m高分辨率DEM数据获取“两段法”中所需要的岸坡剖面数据。
1.2水下及水上起算点
由0.5m×0.5m高分辨率航空影像目视解译提取多年最高洪水位线,水下起算点则通过获取每条岸坡地形剖面线与多年最高洪水位线的交点得到; 水下计算终点即为水上起算点。
1.3水下及水上稳定坡角
水下及水上稳定坡角通过野外实测和室内实验获取(刘娟等, 2010),野外调查中通过实际测量,获取稳定坡角值,同时根据实际量测位置的岩土体室内土力学实验结果进行校核。
1.4水下及水上计算终点
由设计洪水位线与岸坡地形剖面线的交点处高程与该点处毛细水上升高度求和得到Hd,由起始点沿剖面线在水平面投影方向和竖直角α作射线与Hd高程水平面相交,交点即为水下计算的终点; 水上计算终点为实际剖面线与水上稳定坡面线的交点。
2 “两段法”进行塌岸空间三维预测的GIS实现
本文以2.5m×2.5m高分辨率DEM数据作为塌岸区剖面线获取的基础数据,采用GIS组件开发模式实现了“两段法”在三维空间上的体积计算和形态展示。
2.1塌岸三维预测原理
算法设计建立在“两段法”塌岸预测的基础上,将塌岸预测拓展到三维空间中,如图1b所示。图1b将图1a进行了空间上的扩展,即将实际的空间三维岸坡作为预测对象,以与河流多年最高洪水位线近垂直的岸坡地形剖面线作为原始岸坡线,按给定距离间隔 (图1b 中“步长”所示),做n条河流剖面线,覆盖整个预测塌岸区域。以图1b中AC地形剖面线为例,通过水下起算点A,水下稳定坡角α和水下计算终止条件,得出水下稳定岸坡线AB; 通过水上起算点B,水上稳定坡角β和水上计算终止条件计算得到水上稳定岸坡线BC,并同时得到AC地形剖面线所对应的塌岸宽度Sk。

图2 “两段法”塌岸预测程序流程Fig. 2 The flow diagram of Two Section method in bank failure
“两段法”的二维图解只能计算塌岸宽度,同时,稳定岸坡线不能在三维空间中很好地展现,因此,“两段法”在三维空间的拓展,使得塌岸的体积计算和坡形展示成为可能。即图1a中所示,通过一定的水平距离,在水下稳定岸坡线和水上稳定岸坡线上提取点,结合α、 β和起算点A的三维坐标,计算得到分布在水下稳定岸坡线和水上稳定岸坡线上一系列三维坐标点,依此类推,得到塌岸预测范围内由每一条地形剖面线所在的塌岸段进行预测后稳定岸坡线的三维坐标点集合,最终得到该塌岸预测区域内的三维点集,通过该三维点集,可生成塌岸后DEM数据,结合岸坡原DEM即可计算塌岸体积,并能通过可视化的方式将塌岸后的岸坡形态进行三维展示。具体的程序实现流程(图2)。
2.2塌岸三维预测实现
本文采用C#编程语言,基于Visual Studio 2010集成开发环境,结合ArcGIS Engine(简称AE)二次开发组件(ESRI, 2010; 兰小机等, 2011),以插件设计方式实现了二维塌岸宽度计算和三维塌岸体积计算。

图4 “两段法”塌岸体积计算过程Fig. 4 Bank collapse volume calculation by Two Section method

图3 “两段法”的二维GIS实现Fig. 3 The computation of Two Section method through 2D-GIS
2.2.1塌岸宽度计算的实现
根据两段法的二维图解原理,设计宽度计算工具按钮,在DEM数据平面进行剖面线的绘制,即通过绘制线段,生成剖面,并同时计算该直线与多年最高水位线、设计洪水线以及岩层界线的交点。与多年最高洪水位线的交点即为水下稳定岸坡计算的起点;以水下稳定坡角角度为方向,做射线与设计洪水位线所在平面的交点,即为水上稳定岸坡的起算点;再以水上稳定岸坡坡角角度为方向,做射线与实际剖面线相交,即可得到塌岸发生的后缘点,最终生成水上稳定岸坡线,通过计算水上稳定岸坡线长度与水上稳定岸坡坡角的余弦的乘积即可得到塌岸的宽度。
为了使计算过程可视化,在设计该插件的过程中,借助AE的地图容器,将生成的实际剖面线、水下稳定岸坡线、水上稳定岸坡线、水下起算点、水上起算点、塌岸终止点以及其他辅助图形要素绘制在该地图容器中(图3),虚线框中内容即为两段法进行塌岸宽度的可视化解算过程。整个计算的前提是用户绘制一条与多年最高洪水位线、设计洪水位线以及岩层分界线相交的线段,并在绘制线段完成后通过“两段法基本参数设置”对话框,设置两段法计算所需基本参数(图4a),二维图解的过程即可自动完成,需要说明的是,所绘制的线段的方向应与河流走向大致正交。
2.2.2塌岸体积计算的实现
根据两段法的三维图解原理,设计体积计算工具按钮,体积计算建立在宽度计算的基础之上,即将所绘制的剖面线向其左右两侧进行阵列,生成一系列等间隔的剖面线,覆盖一定库岸段,然后,每个剖面线按照计算宽度的过程进行,最终生成一定范围内的塌岸相关数据。
虽然三维“两段法”从严格意义上讲不是真正的三维,应属于“伪三维”或“假三维”的范畴,但将其进行扩展之后,可近似得到三维空间上的计算结果,也是一种较好的选择。
“两段法”在进行山区峡谷型水库的塌岸预测中得到了广泛的应用,本文在“两段法”的基础上,采用GIS二次开发的方式,使得“两段法”的应用由二维空间扩展到三维空间,三维“两段法”的优势主要表现在:
(1)基于高分辨率DEM数据,完成了塌岸二维宽度计算和三维塌岸体积计算,并最终生成可移植的塌岸计算工具插件,适用于GIS基础平台和二次开发应用。
(2)实现了塌岸宽度和体积计算的参数化和自动化以及塌岸预测过程的可视化,使塌岸宽度和体积的计算更加快捷高效,且能生成塌岸预测后岸坡形状,便于进行三维可视化展示。
3 应用实例分析
本文在金沙江下游溪洛渡水库站库区200km回水区塌岸调查的基础上,以获得的典型塌岸区为例,以代表实际存在的3种塌岸情况为例,验证本文提出方法的可行性与适用性。在采用三维“两段法”进行体积计算之前,首先进行塌岸宽度的预测,即通过在塌岸区绘制若干典型剖面进行二维塌岸宽度计算,通过塌岸宽度计算可得到两种结果: ①蓄水后将产生塌岸。即通过可视化的塌岸宽度计算结果(图3),若水下和水上塌岸预测线位于原始剖面线之下,则可判定该塌岸段蓄水后将产生塌岸,并可计算出塌岸的宽度,然后再进一步采用三维“两段法”进行塌岸体积和形态的预测。 ②蓄水后不产生塌岸。通过可视化的塌岸宽度计算(图3),若水下塌岸预测线位于原始剖面线之上,则可判定该塌岸段蓄水后不产生塌岸。以米西洛、对坪和石板滩库岸为例,对三维“两段法”的实际应用进行分析。
3.1应用实例1:米西洛塌岸范围预测
米西洛塌岸区位于美姑河右岸,距河口6.1km,顺河长度1.0km,为崩坡积堆积体,堆积物主要为碎石土,块石少见,碎石弱胶结,主要成分为灰岩。坡体前缘较陡,坡角35°~39°, 900m高程以上为相对平缓台地,两侧均为基岩陡坎。中部前缘发生局部次级滑坡(图5)(镜向: 211°),坡体上有多条冲沟发育,冲沟深度10~20m,沟底未见基岩。前缘下游侧临河附近基岩出露,有采矿。

图5 米西洛塌岸区全景照片Fig. 5 The Panorama picture of Mixiluo bank failure region
根据DEM采用图解的方式,获得该塌岸区的水下稳定坡角为25°,水上稳定坡角为42°,采用三维“两段法”对米西洛库岸段进行水下塌岸预测线和水上塌岸预测线的绘制,步骤如下:
3.1.1塌岸宽度计算
根据图4a设置塌岸预测参数,设置水下稳定坡角为25°,水上稳定坡角为42°,通过绘制剖面线的方式在其上半平面完成可视化计算,如图6a所示,可见,水下塌岸预测线和水上塌岸预测线均位于岸坡坡面线以下。

图6 (a)二维剖面上宽度预测示意; (b)塌岸范围预测Fig. 6 (a)The diagram of bank failure width of 2-D profile; (b)The bank failure region prediction
3.1.2塌岸范围预测
根据图4a设置塌岸预测参数,设置水下稳定坡角为25°,水上稳定坡角为42°,然后进行跨度设置与步长设置,分别设置为450m和25m,即在图6b所示的图切剖面线两侧各450m范围内,以25m间隔生成剖面线集合,分别计算每条剖面上的塌岸宽度,并得到每条剖面线对应的塌岸后缘点,将塌岸后缘点的连线构造塌岸后缘线,再结合600m蓄水位线,以及野外调查获取的塌岸边界线生成塌岸范围,如图6b所示,在水下和水上塌岸预测线上等间隔取点,并根据水上和水下稳定坡角,计算高程,得到三维点集合。

图7 采用挖填方工具计算塌岸体积Fig. 7 Compute the bank failure volume through cut-fill tool in ArcGIS
3.1.3体积计算
体积计算则采用ArcGIS的空间分析功能完成,即将塌岸预测线上的三维点,以“Topo to Raster”的方式生成DEM,最终完成体积计算。通过将图7b所示塌岸后DEM可将其三维形态在ArcScene中进行展示。在此过程中,虽然自动化的方法生成了三维点数据,但会出现自动化不能处理的情况,应引起注意,如图8 所示,在该岸坡左侧边界部分,水下塌岸预测线位于实际剖面线之上,则表明该处无塌岸; 在该岸坡右侧边界处,水上塌岸预测线为空,其后缘点应位于野外调查所获得的堆积体边界线上。通过应用实例2和应用实例3对应用实例1中左右边界产生的两种情况进行详细说明。
3.2应用实例2:对坪塌岸范围预测
对坪岸坡段位于金沙江左岸,距坝里程157.7km,顺江长度0.25m。上下游两侧均以大型支沟为界,为金沙江阶地河流相冲积物堆积(图9)(镜向: 180°)。堆积物主要为河流相砂砾石,具斜层理,含少量砾石,砾石成分为砂岩为主,部分为板岩、砂页岩,混杂少量洪积物堆积,呈棱角状碎石。其上为对坪镇。坡前为坡积物,块石、黏土含量较多。通过对该区实测与图解方法得到的稳定坡角进行综合,得到水下稳定坡角18°,水上稳定坡角23°。

图8 自动化塌岸预测结果分析Fig. 8 The analysis to the results through automatic bank failure prediction

图9 对坪塌岸区全景照片Fig. 9 The panorama picture of Duiping bank failure region
先进行塌岸宽度计算,如图10 所示,水下塌岸预测线位于剖面线之上,表明无塌岸,在该岸坡段进行了多个位置处的试验之后,均出现这一情况,可判断该区域蓄水后基本无塌岸,与该区段河流侵蚀所形成的阶地以及河流相砂砾石堆积物所形成的缓坡地形的特征是一致的。
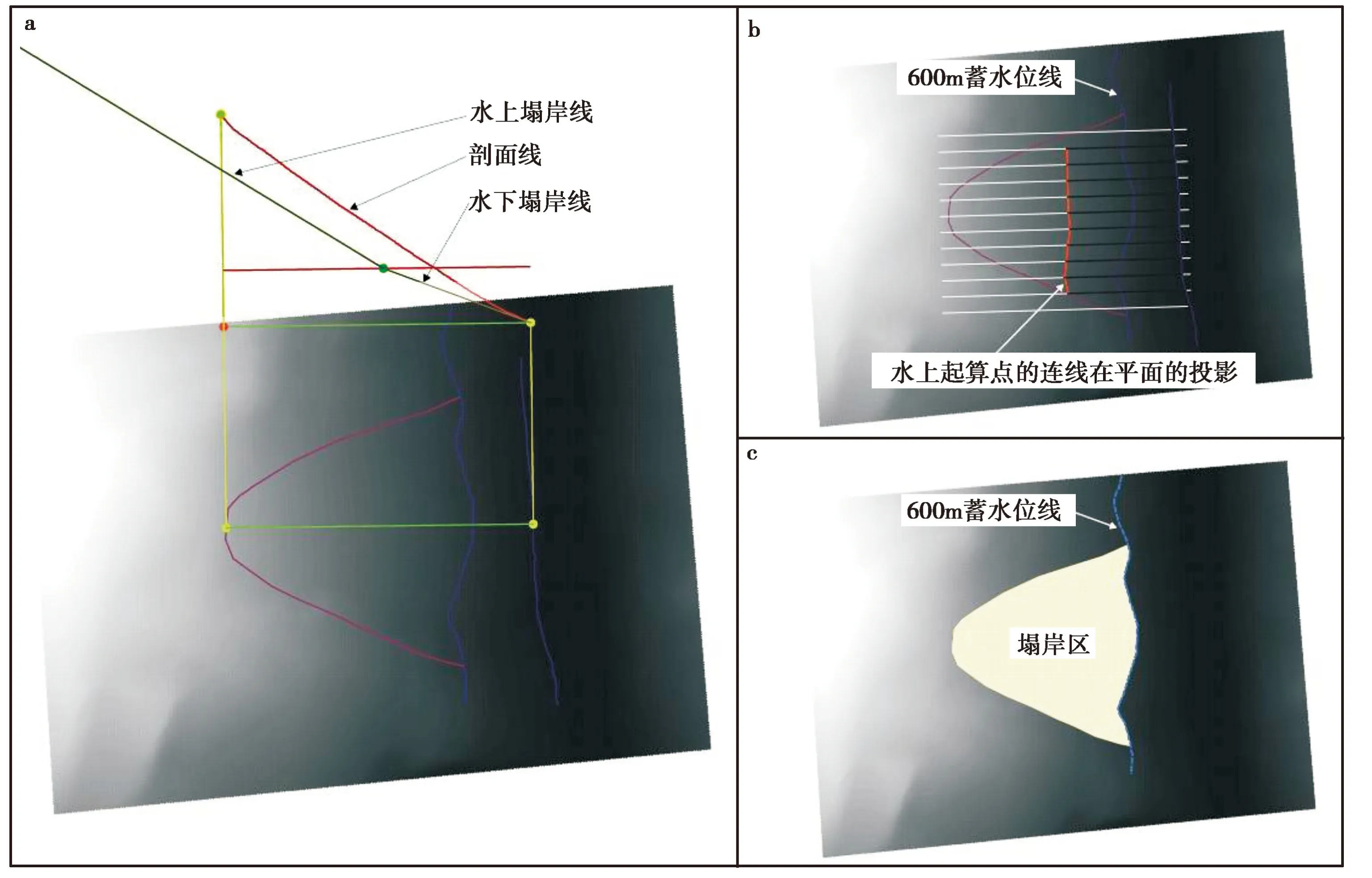
图12 石板滩库岸段宽度预测和范围预测Fig. 12 Width and region prediction of Shibantan prediction

图10 对坪库岸段二维剖面上宽度预测示意Fig. 10 The diagram of width prediction in 2-D profile of Duiping bank failure region

图11 石板滩塌岸区全景Fig. 11 The panorama picture of Shibantan bank failure region
3.3应用实例3:石板滩塌岸范围预测
石板滩库岸段位于金沙江右岸,全景照片如图11(镜向: 153°)所示,通过图解和实测方法的综合,得到其水下稳定坡角为21°,水上稳定坡角为32°。
仍从塌岸宽度计算开始,由图12a可知,水下塌岸线位于剖面线之下,表明该处将会产生塌岸,而水上塌岸线按水上稳定岸坡角绘制射线时,与剖面线无交点,因此,对于该类塌岸,塌岸后缘点即为剖面线的后缘点,塌岸的宽度为该点与600m正常蓄水位线所对应的原始岸坡上的点的连线。
通过体积计算工具,生成一组剖面线,进行每条剖面线上宽度计算,结果如图12b所示,由水上起算点做射线计算时,均与实际剖面线无交点,因此,塌岸后缘线即为野外调查获得堆积体后缘边界线,其塌岸范围即为由600m正常蓄水位线与堆积体边界线构成的多边形(图12c)。
4 结 语
本文在“两段法”的基础上,采用GIS二次开发的方式,使得“两段法”的应用由二维空间扩展到三维空间,主要取得了以下认识:
(1)基于高分辨率DEM数据,完成了塌岸二维宽度计算和三维塌岸体积计算,并最终生成可移植的塌岸计算工具插件,适用于GIS基础平台和二次开发应用。
(2)实现了塌岸宽度和体积计算的参数化和自动化以及塌岸预测过程的可视化,使塌岸宽度和体积的计算更加快捷高效,且能生成塌岸预测后岸坡形状,便于进行三维可视化展示。
总之,GIS技术的引入,使得“两段法”能够更准确更高效地预测塌岸宽度、体积、坡形等特征,为塌岸的防护措施及防护工程的建设提供了参考。但正如“两段法”的提出者王跃敏所述,用该方法时要辅助以其他方法进行对比分析,反复检验其合理性。
Andrew S,Andrew J C C. 2002. Quantifying the mechanical and hydrologic effects of riparian vegetation on streambank stability[J]. Earth Surface Processes and Landforms, 27:527~546.
ESRI. 2010. ArcObjects Help for. NET developers[EB/OL]. http:∥resources.arcgis.com/enhelparcobjects-net/conceptualhelp/
He L D,Zhu X J. 2007. Retrospection and evaluation of prediction method for reservoir bank ruin[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 28(2): 69~72.
Lan X J,Liu D E,Wei R J. 2011. GIS application development based on arcobjects and C#.NET[M]. Beijing: Metallurgical Industry Press: 36~49.
Langendoen E J, Simon A, Curini A, et al. 1999. Field validation of an improved process-based model for streambank stability analysis[J]. International Conference on Water Resources Engineering Proceedings: 1~10.
Liu J,Hu X W,Wang J Q, et al. 2010. Relationship between underwater stable slope angle and granularity composition of loose deposit[J]. Advances in Science and Technology of Water Resources, 30(4): 71~75.
Liu T X, 2006. Study on the methods of Predicting reservoir bank collapse in the Three Gorges areas[D]. Chengdu: Chengdu University of Technology
Millar R G,Quick M C. 1993. Effect of bank stability on geometry of gravelrivers[J]. Journal of Hydraulic Engineering, 119: 1343~1363.
Millar R G. 2000. Influence of bank vegetationon alluvial channel patterns[J]. Water Resources Res,36(4): 1109~1118.
Natasha P,Andrew S,Eddy L. 2007. Enhancements of a bank-stability and toe-erosion model and the addition of improved mechanical root-reinforcement algorithms[J]. World Environmental and Water Resources Congress: 1~11.
Osman A M,Thorne C R. 1998. Riverbank stability analysis. Part I:Theory[J]. Journal of Hydraulic Engineering ASCE,114(2): 125~150.
Parker C, Simon A, Thdrne C R. 2008. The effects of variability in bank material properties on riverbank stability: Goodwin Creek, mississippi[J]. Geomorphology,101(4): 1533~543.
Que J S. 2007. Study on nonlinear prediction for reservoir bank collapse in fuling area of the Three Gorges project[D]. Changchun: Jilin University.
Simon A, Langendoen E J, Thomas R E. 2003. Incorporating bank-toe erosion by hydraulic shear into a bank-stability model: Missouri River, Eastern Montana[J]. American Society of Civil Engineers Water Resources Conference Proceedings: 70~76.
Simon A, Polen N, Langendoen. 2007. Enhancements of a band ̄stability and toe ̄erosion model and the addition of improved mechanical root ̄reinforcement algorithms[J]. Word Environmental and Water Resources Congress: 1~11.
Wang Y M,Tang J H,Ling J M. 2000. Study on prediction method for reservoir bank caving[J]. Chinese Journal of Geotechnical Engineering, 22(5): 569~571.
Wang Z L. 2005. The extenics studying on the bank caving prediction of changshou area along Three Gorges reservoir[D]. Changchun: Jilin University.
Wood A L, Simon A, Downs P W, et al. 2001. Bank-toe processes in incised channels: the role of apparent cohesion in the entrainment of failed bank materials[J]. Hydrological Processes,15(1): 39~61.
Xu Q,Liu T X,Tang M G,et al. 2007. A new method of reservoir bank ̄collapse prediction in the Three Gorges reservoir—river bank structure method[J]. Hydrogeology & Engineering geology,(3): 110~115.
Zhang Z Y,Wang S T,Wang L S. 1994. Engineering geology analysis theory[M]. Beijing: Geological Publishing House: 563~570.
何良德,朱筱嘉. 2007. 水库塌岸预测方法述评[J]. 华北水利水电学院学报, 28(2): 69~72.
兰小机,刘德儿,魏瑞娟. 2011. 基于ArcObjects与C#.NET的GIS应用开发[M]. 北京:冶金工业出版社: 36~49.
刘娟,胡卸文,王军桥,等. 2010. 松散堆积体水下稳定坡角与粒度成分的关系[J]. 水利水电科技进展,30(4): 71~75.
刘天翔. 2006. 三峡库区塌岸预测方法研究[D]. 成都:成都理工大学.
阙金声. 2007. 三峡工程涪陵区水库塌岸非线性预测研究[D]. 长春:吉林大学.
王跃敏,唐敬华,凌建明. 2000. 水库坍岸预测方法研究[J]. 岩土工程学报,22(5): 569~571.
王征亮. 2005. 三峡库区长寿区库岸塌岸预测的可拓学研究[D]. 长春:吉林大学.
许强,刘天翔,汤明高,等. 2007. 三峡库区塌岸预测新方法——岸坡结构法[J]. 水文地质工程地质,(3): 110~115.
张倬元,王士天,王兰生. 1994. 工程地质分析原理[M]. 北京:地质出版社: 563~570.
PREDICTION OF RESERVOIR BANK SLOPE FAILURE USING DEM-SUPPORTED TWO SECTION METHOD
WANG Xiaodong①DAI Fuchu①②HUANG Zhiquan①
(①NorthChinaUniversityofWaterConservancyandElectricpower,Zhengzhou450011) (②BeijingUniversityofTechnology,Beijing100124)
In this article we expand applications of “Two Section Method” from two-dimension to three-dimension. We use the Microsoft Visual Studio where meantime ArcGIS Engine component is embedded. The software program is designed to compute the width and volume of reservoir bank slope failure. By inputting some parameters including stable slope angle, lithological boundary and flood level line, it automatically runs. Hence, the prediction of bank slope failure can be completed via simple man-machine interaction, which improves the efficiency of prediction. At the meantime, the bank slope shape can be comprised between,before and after bank failure through three-dimension visualization, which can provide more reliable support of data and decision for bank protecting project. In the process of software program, there are three ways of achieving the parameters according to the need of program. They are: (1)Using the field survey and geotechnical test results, the parameters such as bank slope angle stabilized above and underwater, can be obtained,(2)From the geological map and high-resolution Images, lithological boundary, flood level line and low level line can be achieved, and (3)From high-resolution DEM,the terrain profile line can be drawn that acts as the terminal condition of the program.
DEM, Two Section method, Bank failure, ArcGIS Engine
10.13544/j.cnki.jeg.2016.01.005
2014-09-02;
2015-02-27.
河南省重点科技攻关项目(152102210111),河南省科技创新人才计划(154100510006),华北水利水电大学高层次人才引进科研启动项目(201201,201402),华北水利水电大学青年科技人才创新计划(70461)资助.
王小东(1980-),男,博士,讲师,主要从事GIS, 滑坡、水库塌岸等方面的研究. Email:wxdyaner@foxmail.com
简介: 黄志全(1970-),男,博士,教授,博士生导师,主要从事岩石力学,地质工程方面的研究. Email:huangzhiquan@ncwu.edu.cn
TV62
A

