基于最小二乘法的风机变桨系统故障预警

姚万业，杨金彭

(华北电力大学 自动化系，河北 保定 071003)



基于最小二乘法的风机变桨系统故障预警

姚万业，杨金彭

(华北电力大学 自动化系，河北 保定 071003)

提出了一种新的风机变桨系统故障预警方法.通过最小二乘法拟合历史数据曲线，形成正常运行状态下的健康模型.采用基于欧氏距离的方法对输出残差进行统计分析,确定预警阈值并计算异常率作为触发预警指标.最后，以风速和1#叶片桨距角为例，选择处于额定风速到切出风速之间的数据作为研究对象，经过在Matlab仿真表明：该方法能够准确地对风机变桨系统进行故障预警，具有一定的可行性.

最小二乘法；健康模型；残差分析；预警阈值

随着风电的不断发展，风电场规模越来越大.风能作为一种新能源，为实现长期稳定发展的目标，必须控制成本.风场的成本主要分为两个方面[1]，其一是风机制造、加工和安装成本，其二就是运维成本.风场一般建在偏远地带，风机工作环境十分恶劣，加上风资源的随机性，风机的运行工况复杂多变.为了适应如此复杂多变的工况，大多数风场采用变桨控制技术.复杂工况下，频繁地变桨动作势必会导致变桨装置的故障多发，为降低风机运维成本，对于故障频发的大部件实现在线预警和诊断意义重大.

风场每天产生海量的历史数据，既包括正常数据，也包括故障信息，这些数据潜在的信息对于风场政策制定及高效管理具有很高的利用价值.如何对数据进行挖掘、分析，将分析结果作为故障预警的依据已经成为风场关注的焦点.国内外对故障预警算法的研究很多，其中NEST算法研究比较深，应用场景比较广；最小二乘法以其处理思路简单、计算量相对较小，且适用于耦合性较高的参数等优点越来越受到人们的青睐[2].

1　最小二乘法原理

1.1最小二乘曲线拟合

通过给定的一组历史数据{(xi,yi),i=0,1,2......m}，基于最小二乘原理，求变量x和y之间的函数f(x,A)，即基于大量历史数据样本求得一条曲线，使样本数据点均在此曲线上或离曲线不远处，它不仅能够反映数据的总体分布情况，并且在局部也不会出现较大的波动，也反映了原始数据的变化特性[3].此方法旨在通过寻找函数f(x)使得计算偏差Δy=f(xi)-yi,i=(1,2,3.....n)的平方和最小，即

(1)

式(1)中，R2表示最小偏差平方和，n为样本数据数量.

最小二乘拟合首先要确定函数f(x)的形式，一般相关性较好的数据，通常选用多项式拟合模型，即

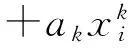
(2)

式(2)中，ai(i=0,1,2......k)为模型中待确定的系数，k值一般因现场实际情况而定，多取为3或4.

要使得R2值最小，系数ai应满足式(3)所示最小二乘原则：

(3)

将式(1)代入到式(3)中，经过计算得系数矩阵A为

A=(XTX)-1XTY，

(4)

1.2基于欧式距离的偏差度分析

基于最小二乘法将历史数据拟合成一条曲线.在允许范围内，以拟合函数计算值作为预测值.为了很好的描述f(x)的拟合值与真实值之间的离散程度，引入偏差度ε，即

(5)

由于拟合数据样本足够大，且对输入模型进行预测时存在不确定性.经统计分析，偏差度ε服从正态分布，且99.35%的数据在[μ-3δ,μ+3δ]范围内，几乎可以代表所有数据[4].依据现场经验，可认为偏差度ε在[μ-3δ,μ+3δ]范围内为正常数据，否则为异常信息.

2　数据预处理

本文选用河北赤沽风场历史数据作为统计样本，以10分钟为采集间隔 ，取自SCADA系统中2015年2月10日至2016年2月10日数据作为样本库，通过对变桨系统1#叶片桨距角的变化情况计算作为预测性能指标[5].对于样本数据选择主要依据以下几个原则：

(1) 选取额定风速到切出风速之间数据作为统计样本.对于变桨角度，当风速达到额定值时，为了控制输出功率，变桨角度会在0～25度之间变化，故样本库中不应包含此范围外的数据.

(2) 参考风速的功率图，剔除风机不工作点的数据，即风速在正常发电范围内，风机没有产生功率时刻的数据.

(3) 剔除风机由于阵风或其他偶然因素所产生的异常数据点.

(4) 剔除风机在故障时刻产生的数据.

文中所有样本数据均来自于金风1 500 kW机型机组的运行数据，该机型基本信息如表1所示：

表1　金风1 500机组基本信息表

3　曲线拟合及残差分析

依据数据预处理原则，对样本数据库进行预处理，以1#叶片桨距角随风速变化作为处理参数，图1为处理前后对比：

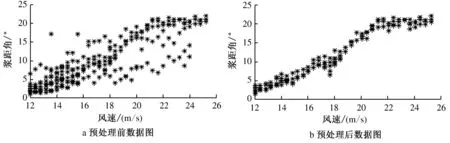
图1　数据预处理前后对比图

从图1中两图对比可知，经过预处理后，大多数奇异点和故障点对数据分析的影响基本可以排除，预处理后的数据基本能够代表变桨系统正常运行情况下变桨角度随风速的变化情况.采用最小二乘法对变桨角度和风速进行曲线拟合，拟合结果的函数表达式为

y=-0.007 5x3+0.147x-0.1x+7.

(6)

为验证曲线是否能够准确地表示正常运行工况下桨距角变化情况，对其计算输出值做残差分析，对于统计样本数据采用欧式距离的方法计算拟合值与历史值残差，计算结果如表2所示：

表2　残差分析

覆盖率是指拟合曲线能代表实际正常运行工况的程度[6].由表2可见，拟合曲线覆盖率为98.86%，理论上可以认为此拟合曲线即可表示实际工况.在实际运行过程中，对于任意实时风速，在允许偏差范围内，角度参数都应符合拟合曲线的变化规律，否则处于异常状态，若长时间处于异常状态则进行故障报警.

4　验证

选取河北赤沽风场SCADA系统中2016年3月10日14:00至2016年4月10日18:00期间的数据作为测试样本，以10分钟为采集单元，对数据进行预处理后得到200组异常工况测试样本数据集，将200组测试数据代入健康模型中，即式(6)，结果如图2所示：

图2　故障异常点检测图

在图2中，0代表正常数据点，1代表异常数据点，由图得出大约从第40个采集点开始，测试数据开始有异常值出现，且异常率不断增大，到最后达到100%的异常率.根据预警原则对异常数据出现且异常率不断增大时刻进行报警，对SCADA系统的记录信息查询，结果如表3所示：

表3　SCADA信息记录表

分析图2并结合表3可知：第40～50采集点期间为正常状态向故障过渡时期，到第50个采集点运行工况已为故障状态，根据预警规则在第40个采集点左右进行故障预警，能够准确的起到对故障预测的功能，从而进行提前安排检修计划，这对于风场进行经济、高效地运行有着重要的现实意义.

5　结语

文中通过对河北赤沽风场一年的桨距角和风速数据进行统计分析，挖掘出大量潜在的高价值信息.采用最小二乘法拟合出正常运行工况下的健康模型，并基于欧氏距离法对拟合预测值和历史值的残差进行了统计分析，基于现场经验并结合残差分析结果设定预警阈值和预警规则.最后通过对故障数据进行仿真验证，结果表明该方法在预警功能实现上具有很高的准确率，可以有效防止故障发生，在故障发生前通过预警信号及时将故障排除，从而提高了风机运行地安全性和经济性.

[1]王朝华.国际新能源发展的主要趋势及对我国新能源发展的思考[J].经济论坛，2011,495(10):84-89.

[2]吴恵荣.统计学原理[M].上海:上海交大出版社，2000.

[3]朱勇华.应用数理统计学习指导[M].武汉:武汉大学出版社，2002.

[4]高祥宝，董零青.数学分析与SPSS应用[M].北京:清华大学出版社，2007.

[5]陈子斯.基于风电机组SCADA数据的故障预警预测方法研究[J].电力技术与应用,2011,95(11):219-227.

[6]李大中，许炳坤，常城.大型风电机组现场运行数据预处理及模型建立[J].国网技术学院学报，2015,18(3):6-10.

责任编辑：赵秋宇

Fault Early Warning of Wind Turbine Pitch System Based on Least Square Method

YAO Wan-ye, YANG Jin-peng

(DepartmentofAutomation,NorthChinaElectricPowerUniversity,Baoding071003,China)

The paper puts forward a new fault warning method of the draught fan variable propeller system by the least squares method fitting historical data curve so it can become a health model under the normal operation.Then according to Euclidean Distance method,the paper satistically analyzes the output residual error, determines the warning threshold value and takes the abnormal rate calculation as trigger warning index.Finally taking the wind speed and 1# blade pitch angle as an example, the paper chooses the data between rated wind speed and cut out wind speed as the research object, through the Matlab simulation test, which shows that this method can accurately warn the fault of draught fan variable propeller system forecast and feasibiility.

deep mining;least square method;health model;residual analysis

2016-05-10

姚万业(1965—)，男，北京人，教授，博士，研究方向：计算机网络技术.

1671-9824(2016)05-0040-04

TM73

A