基于改进壳-柱模型的盾构隧道饱和地基动应力解

狄宏规， 周顺华， 陕　耀， 何　超

(同济大学 道路与交通工程教育部重点实验室, 上海 201804)



基于改进壳-柱模型的盾构隧道饱和地基动应力解

狄宏规， 周顺华， 陕耀， 何超

(同济大学 道路与交通工程教育部重点实验室, 上海 201804)

针对现有壳-柱模型无法考虑盾构隧道壁后注浆层的问题，分别采用无限长的双层圆柱壳模拟盾构隧道衬砌和壁后注浆层，中空圆土柱模拟饱和地基，基于Flügge圆柱壳理论和Biot波动理论，结合边界条件，求解隧道内作用固定简谐荷载时饱和地基中的动应力，并分析其分布规律及注浆层对土体动应力的影响.结果表明：隧道注浆层底部土体径向正应力τrr和孔压Pf幅值随着与荷载的轴向距离增大而减小，剪应力τrz随距离增加先增大后减小，至3D(隧道直径)时地基动应力接近于0；土体的渗透性越差，径向正应力和孔压幅值越大，但当土体渗透系数k小于10-5m·s-1时，渗透系数的进一步减小对地基动应力幅值的影响不大；隧道壁后注浆层能减小土体径向正应力和孔压(约5%～8%)；注浆层下方同一点土体径向正应力和孔压幅值均随着注浆层厚度增加而线性减小；而注浆层的弹性模量在一定范围内(50～650 MPa)变化时对其几乎无影响.

盾构隧道； 饱和土； 注浆层； 地基动应力

目前，我国地铁的发展已进入大规模建设和安全运营并重的阶段.然而，近年来我国软土地区(如上海、南京等城市)地铁隧道的长期沉降问题逐步凸显，不但影响线路的运营，而且增加了养护维修的费用[1-4].初步研究表明，地铁列车引起的车载累积沉降在工后沉降中占有很大比例，在某些区段甚至是最主要的沉降影响因素[5].由于车载累积沉降始于地基土体应力及孔隙水压力的变化，故列车运行引起的地基动应力的研究是预测车载累积沉降的基础.

国内外学者建立了一系列分析模型来研究地下隧道-地基系统的动力相互作用问题.如Metrikine等[6]用嵌入的欧拉梁模型来研究地下隧道及地基的振动响应；Forrest和Hunt[7]采用薄壁圆柱壳模拟隧道衬砌，中空圆形土柱体模拟弹性地基，提出了三维隧道-地基系统振动分析模型(即PiP模型).随后，Forrest和Hunt[8]和Hussein[9]将浮置板轨道与隧道-地基模型耦合，进一步发展完善了PiP模型；Degrande等[10]利用有限元-边界元法研究了隧道和土体的动力相互作用问题；Gupta等[11]对比了周期性有限元-边界元模型和PiP模型，结果表明两者在分析全空间埋置隧道的振动响应问题时具有较好的一致性；曾晨等[12]在Forrest等[7-8]的基础上，进一步探讨了饱和地基圆形隧道在简谐荷载下的动力响应问题.然而，上述研究均侧重于地下铁路行车导致的环境振动响应，对于车致隧道地基土动应力的研究相对较少.张曦等[13]对上海地铁二号线某区间隧道断面侧面的车致土动应力进行了现场测试，但由于受测试条件的限制，无法给出隧道底部的土动应力和孔压值；宫全美等[14]基于轮轨耦合模型，利用有限元法分析了地铁隧道车致地基动应力的变化规律和影响范围，但尚未考虑隧道壁后注浆层等对地基动应力的影响.总的来说，目前对于地铁盾构隧道车致地基动应力的认识还有待进一步深化.

在实际的盾构掘进过程中，隧道衬砌背面和实际开挖洞壁间存在一定间隙，即盾尾间隙.为减小由于盾尾间隙而产生的应力释放和地层变形，往往需要对施工间隙进行填充注浆(图1)[15].当盾构隧道注浆浆液凝固后，会在隧道衬砌周围形成环向的水泥土注浆层.由于壁后注浆层的材料及参数既不同于隧道衬砌也不同于周围土层，因此是否考虑以及如何考虑盾构隧道壁后注浆层对车致地基动应力的影响是值得进一步探讨的问题.

本文在文献[12]的基础上，进一步考虑盾构隧道壁后注浆层，采用弹性双层圆柱壳模拟盾构隧道衬砌和壁后注浆层，多孔饱和圆柱土体模拟地基，结合边界条件，建立能考虑壁后壁后注浆层的饱和地基圆形盾构隧道动力响应分析模型(改进壳柱法模型).基于上述模型分析地基动应力的分布规律，以及注浆层对地基动应力的影响.研究结果可为软土地区地铁盾构隧道的车载累积沉降计算及相关研究提供参考.

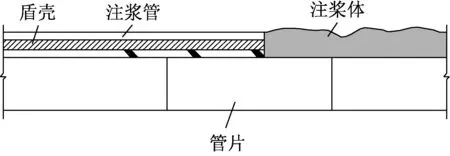
a 盾尾注浆

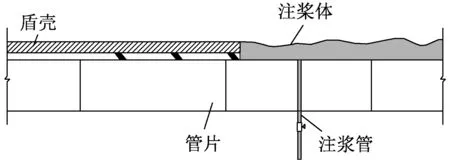
b 管片注浆孔注浆

1　控制方程及求解

1.1双层圆柱壳控制方程

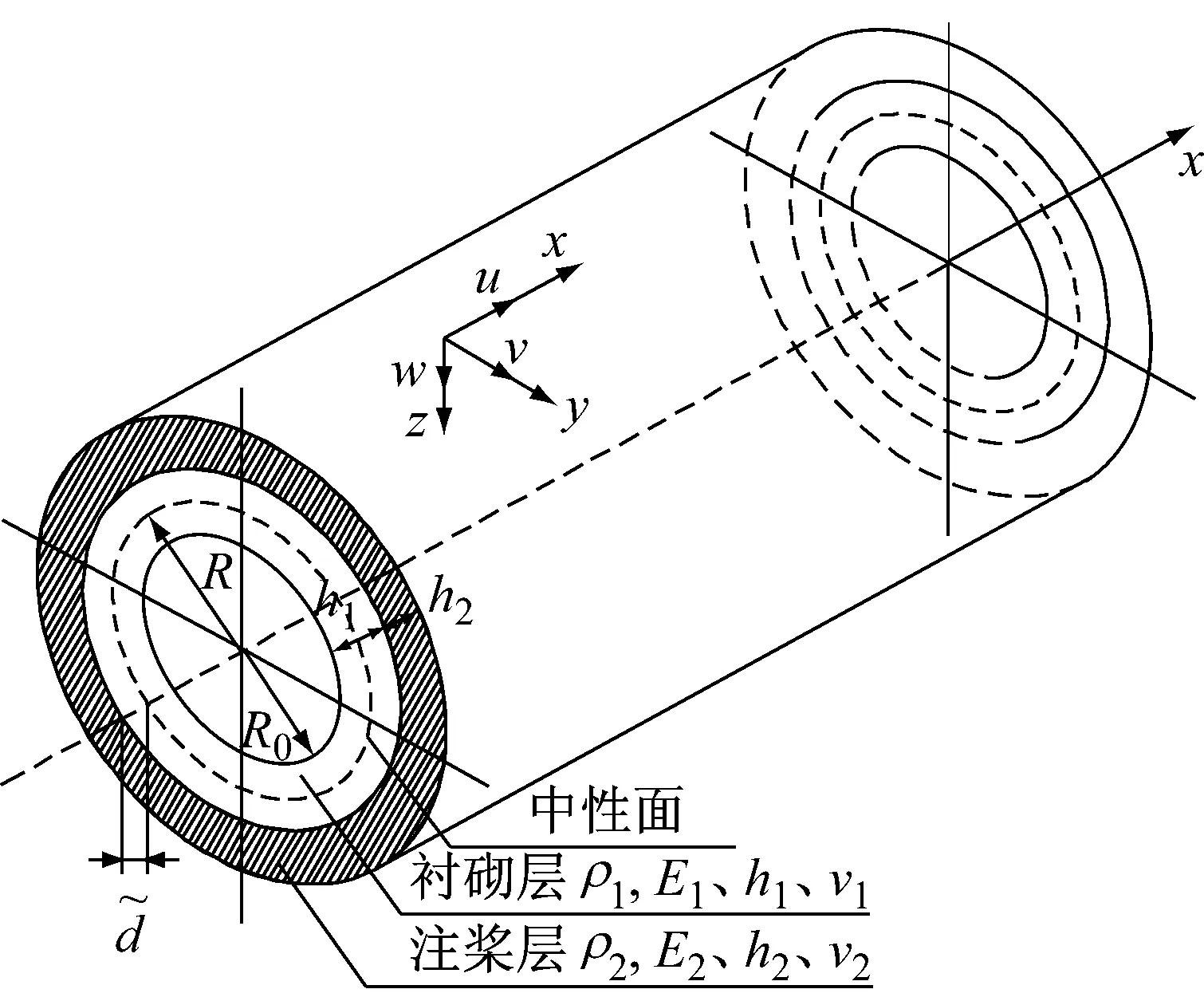
图2　双层圆柱壳及坐标系

Flügge双层圆柱壳的运动微分方程如下：

轴向：

(1)

切向：

(2)

径向：

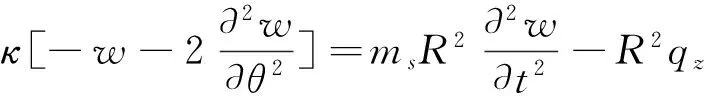
(3)

式(1)—(3)中：ms为双层壳的质量，ms=ρ1h1+ρ2h2；qx、qy和qz分别为壳体中面沿x、y、z方向的净应力.式(1)—(3)中其他参数计算表达式如下：

(4)

假定壳体中面净应力qx、qy、qz具备如下形式：

(5a)

(5b)

(5c)

则衬砌中面沿x、y、z方向的位移u、v、w可表示为

(6a)

(6b)

(6c)

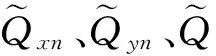
将荷载表达式(5)和位移表达式(6)代入壳体平衡方程式(1)—(3)，写成矩阵形式如下：

(7)

1.2地基土体的波动方程

饱和地基采用中空圆形土柱模拟，如图3所示.圆柱体内径R1等于双层壳(衬砌和注浆层)的半径，外径R2趋于无穷大.er、eθ、ez分别为沿圆柱坐标系主方向r、θ、z方向的位移分量，ur、uθ、uz分别为土骨架沿r、θ、z方向的位移分量.

图3　地基土柱及坐标系

将土体视为多孔饱和介质，引入Biot波动方程，如式(18)所示：

(8)

式中：ui、wi分别为土骨架位移分量和流体相对于土骨架的位移分量；ui、wi上的“·”和“··”分别表示位移对时间求一阶导数和二阶导数；λ、μ为土骨架的Lamé常数；α、M分别为表征土颗粒和孔隙流体压缩性的常数；b=η/kd为反映黏性耦合的参数，η、kd分别为流体的动力黏滞系数和土的动力渗透系数；ρb=n0ρf+(1-n0)ρs，n0为土体的孔隙率，ρf、ρs分别为流体和土骨架密度；m=ρf/n0.

均质饱和多孔介质的本构方程可表示为

(9)

式中：ζ=-wi,i；τij为土体单元总应力；e=ui,i为土骨架的体积应变；εij=(ui,j+uj,i)/2为土骨架应变；δij为Kronecker符号；Pf为孔隙水压力.

根据Helmholtz矢量分解定理，求解Biot波动方程，可得频域-波数域内饱和土体的土骨架位移及总应力的矩阵表达式为[12]

(10a)

(10b)

式中：

D={A1B1A2B2ArBrAzBz}

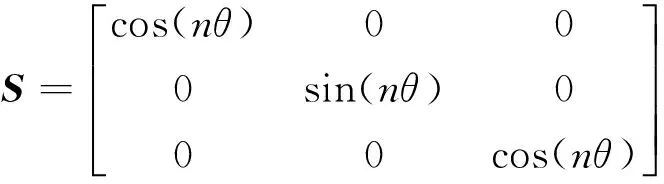
比较式(10)与式(5)—(6)可知，环向模态数n下位移u和应力σ在频率-波数域内的各分量为

(11)

式中：U和T均为3×8的矩阵，矩阵中各元素表达式见文献[12].

(12a)

(12b)

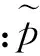
1.3隧道-地基模型的耦合求解

壳-柱模型的相关假定为：①衬砌壳体的应力等于衬砌内外表面荷载所产生应力的差值；②衬砌与地基土体交界面位移、应力均协调；③距隧道中心无限远处土体位移衰减为零.需要注意的是，图2中的轴向(x方向)与图3中的轴向(z方向)相对应.

若在衬砌内表面(x=0、θ=0°)处作用一个沿径向的固定单位简谐荷载eiωt，如图4所示.图4b是将图4a中的集中力(单位简谐荷载)转化成隧道内表面的应力(用空间狄拉克函数表示成的冲击荷载).图中R0·Δθ表示沿θ方向的微小弧长，Δx表示沿x方向的微小弧长.

图4隧道内固定简谐点荷载[7]

Fig.4Harmonic normal point load acting

on the tunnel

则该荷载在x、y、z方向产生的应力分量可以描述成[7]：

(13)

式中：δ(x)和δ(θ)是狄拉克δ函数.

荷载在频率-波数域内的应力分量可写为

(14)

根据第一个边界条件，由式(7)有，在衬砌与土体接触面处:

(15)

注意到图2和图3所采用圆柱坐标系的主方向并不完全一致，根据第二个边界条件，比较两图可得：

(16)

根据第三个边界条件，当土柱外径R2趋于无穷大时，土体位移应为0，可得系数A1=A2=Ar=Az=0，具体见文献[12].

从而可得衬砌与土体接触面处的位移、应力为

(17)

(18)

将式(14)、(17)、(18)代入式(15)中，有：

(19)

假定隧道衬砌不漏水，则隧道与地基边界面孔隙水压法向导数为0，根据式(12)有：

(20)

联立式(19)—(20)，有

(21)

从而得到环向模态数n下r=R处的应力为

(22)

对式(22)进行Fourier 逆变换，即可得时间-空间域内饱和地基中圆柱面内任意一点(r,θ,z) 处的土体应力.

2　算例与分析

分别采用衬砌-饱和地基单层壳模型和衬砌-注浆层-饱和地基双层壳模型计算地基土体动应力.计算结果中的τrr、τrz、Pf分别表示土体应力(由外荷载引起的)的幅值.表1～表3给出了隧道衬砌、注浆层和饱和土体的计算参数.其中，衬砌和饱和土体的计算参数主要参考文献[12].由于砂土(淤泥质黏土)的渗透系数k一般在10-4(10-6)m·s-1数量级，动力渗透系数kd一般在10-8(10-10)m2数量级，流体的动力黏滞系数η取0.01 Pa·s，故本文中反应土体黏性耦合的参数b取106～108N·s·m-4.文献[16]针盾构隧道壁后注浆层参数进行了分析，表3中注浆层的参数主要参考其研究结果.

表1　隧道衬砌计算参数[12]

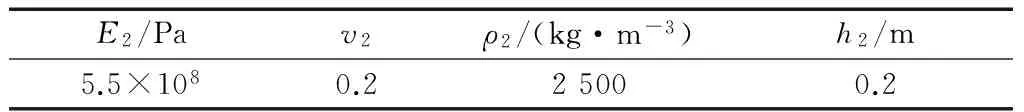
表2　壁后注浆层计算参数[16]

表3　饱和地基土体计算参数[12]

为验证双层壳模型的可靠性，先对双层壳模型进行退化.注浆层材料的计算参数设为与衬砌层相同的值，而衬砌内径R0取2.875 m，衬砌层和注浆层的厚度h1和h2分别取0.05和0.2 m,b=106N·s·m-4.计算f=65 Hz时隧底处(r=3 m,θ=0°)的地基动应力，并和文献[12]中的单层壳模型的计算结果进行对比，见图5.可以看到，两者计算结果一致，表明双层壳计算模型是可靠的.

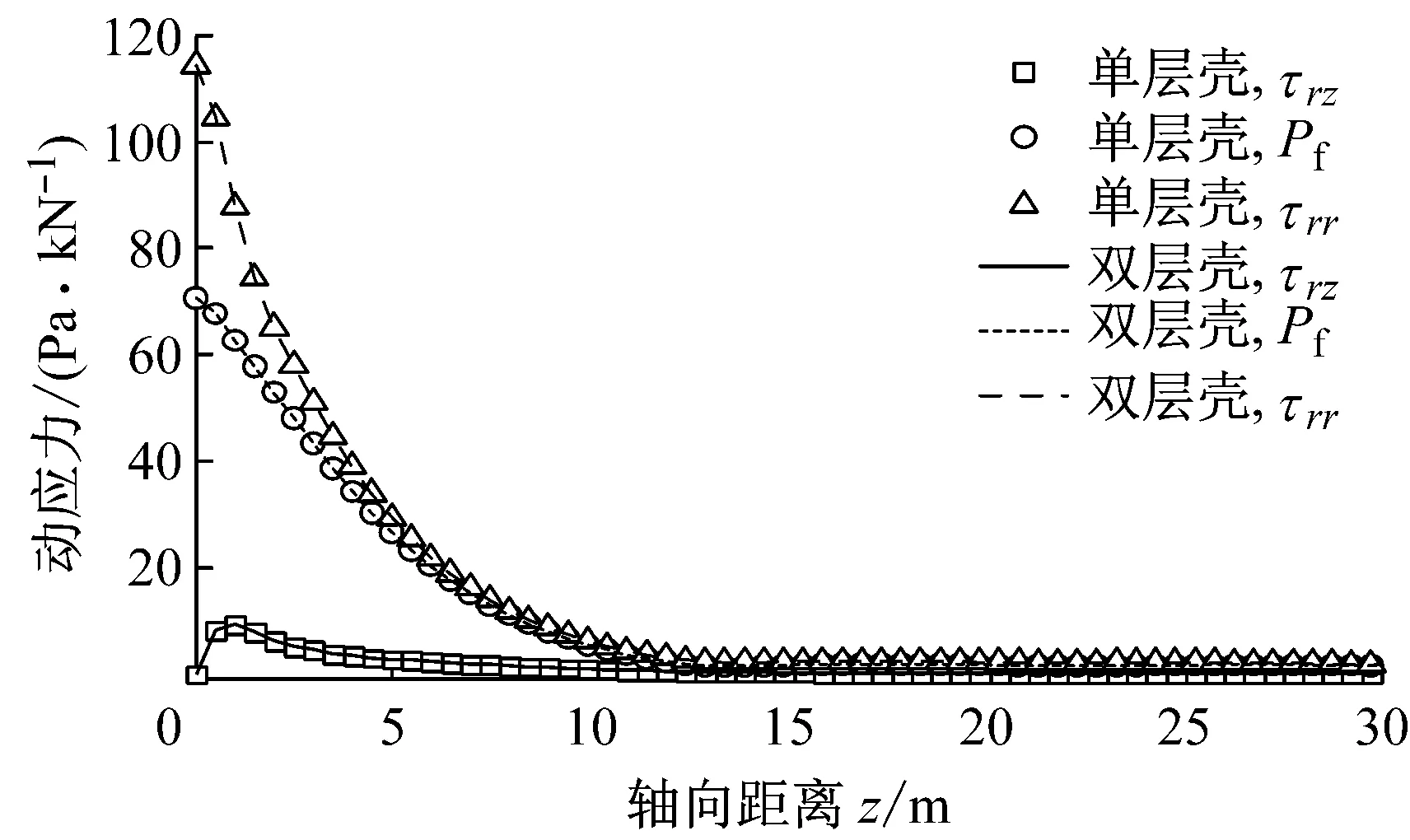
图5　单层壳与双层壳模型计算结果对比图

图6为荷载频率f=65 Hz时注浆层底部地基动应力的轴向分布图，可以看出：注浆层底部土体径向正应力τrr和孔压Pf幅值随着轴向距离增大而减小，最大值在荷载作用点正下方；剪应力τrz幅值随着与荷载的距离增加先增大后减小，最大值在荷载作用点两侧2 m处，当与荷载的轴向距离增至3D(D为隧道直径，6 m)时，地基动应力幅值接近于0.

a 正应力τrr

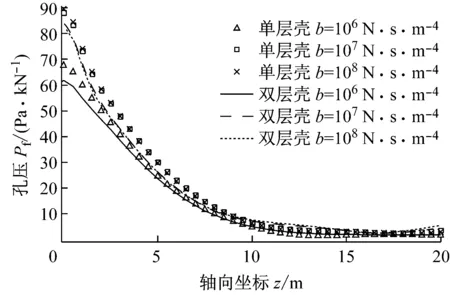
b 孔压Pf

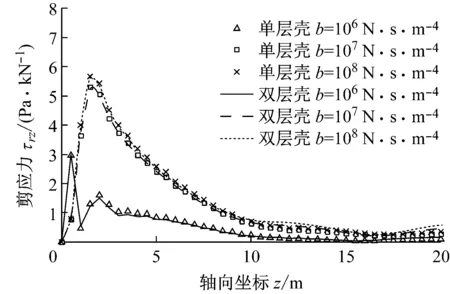
c 剪应力τrz

表4为荷载频率f=65 Hz时单层壳与双层壳模型下注浆层底部地基动应力最大幅值统计，可以看到：(1) 同一位置处单层壳模型计算的地基动应力幅值均大于双层壳模型计算的地基动应力幅值，即注浆层能减小地基动应力，在不同土体渗透性条件下地基径向正应力、孔压和剪应力的最大衰减比分别为5.9%、8.4%和6.1%；且土体渗透性越好，注浆层对地基动应力的衰减比越大.(2) 无论是单层壳还是双层壳模型，土体的渗透性越差(b值越大)，地基动应力幅值越大，但当b大于107N·s·m-4(即渗透系数k小于10-5m·s-1)时，再增大b值对三者的影响都不大.

表4　注浆层底部地基动应力幅值统计

图7给出了注浆层厚度和弹性模量对地基动应力的影响，计算时荷载频率f=65 Hz, 反应土体黏性耦合的参数b=108N·s·m-4，从中可以看出，隧道注浆层下方同一点(r=3.5 m,θ=0°,z=0)土体径向正应力和孔压幅值均随着注浆层厚度增加而线性减小.当注浆层弹性模量在一定范围内(50～650 MPa)时，注浆层弹性模量变化对其下方同一点土体径向应力和孔压几乎无影响.

a 注浆层厚度

b 注浆层弹性模量

3　结论

(1) 隧道注浆层底部土体径向正应力τrr和孔压Pf幅值随着与荷载的轴向距离增大而减小，最大值在荷载作用点正下方；剪应力τrz幅值随轴向距离的增加先增大后减小，最大值在荷载作用点两侧2 m处；当轴向距离增至3D(D为隧道直径)时，地基动应力接近于0.

(2) 地基土体的渗透性越差(b值越大)，土体径向正应力τrr、剪应力τrz和孔压Pf的幅值越大，但当b大于107N·s·m-4(即土体渗透系数k小于10-5m·s-1)时，b值的进一步增大对地基动应力幅值的影响极小.

(3) 隧道壁后注浆层能减小地基土体径向正应力和孔压值(约5%～8%)；壁后注浆层下方同一点土体径向正应力和孔压幅值均随着注浆层厚度增加而线性减小；注浆层弹性模量在一定范围内(50～650 MPa)变化对其下方同一点土体径向应力和孔压幅值几乎无影响.

[1]Shen S L, Wu H N, Cui Y J,etal. Long-term settlement behaviour of metro tunnels in the soft deposits of Shanghai[J]. Tunnelling and Underground Space Technology, 2014, 40, 309.

[2]黄大维，周顺华，宫全美，等. 软土地区地铁不同结构间差异沉降特点分析[J]. 同济大学学报：自然科学版，2013, 41(1): 95.

HUANG Dawei, ZHOU Shunhua, GONG Quanmei,etal. Characteristic analysis of non-uniform settlement for different structures of metro in soft soil districts[J]. Journal of Tongji University： Natural Science, 2013, 41(1): 95.

[3]狄宏规，周顺华，宫全美，等.软土地区地铁隧道不均匀沉降特征及分区控制[J].岩土工程学报, 2015, 37(S2): 74.

DI Honggui, ZHOU Shunhua, GONG Quanmei,etal. Differential settlement of metro tunnels and its zonal control in soft deposits[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(S2): 74.

[4]Huang X, Huang H W, Zhang J. Flattening of jointed shield-driven tunnel induced by longitudinal differential settlements[J]. Tunnelling and Underground Space Technology, 2012, 31: 20.

[5]王常晶. 列车移动荷载作用下地基的动应力及饱和软粘土特性研究[D]. 杭州: 浙江大学, 2006.

WANG Changjing. Study on the dynamic stress in ground indueed by train moving load and cyclic properties of soft saturated clay[D]. Hangzhou: Zhejiang University, 2006.

[6]Metrikine A V, Vrouwenvelder A C W M. Surface ground vibration due to a moving train in a tunnel: two-dimensional model [J]. Journal of Sound and Vibration, 2000, 234(1): 43.

[7]Forrest J A, Hunt H E M. A three-dimensional model for calculation of train-induced ground vibration[J]. Journal of Sound and Vibration, 2006, 294(4/5): 678.

[8]Forrest J A, Hunt H E M. Ground vibration generated by trains in underground tunnels [J]. Journal of Sound and Vibration, 2006, 294(4/5): 706.

[9]Hussein M F M, Hunt H E M. A numerical model for calculating vibration from a railway tunnel embedded in a full-space [J]. Journal of Sound and Vibration, 2007(305)：401.

[10]Degrande G, Clouteau D, Othman R,etal. A numerical model for ground-borne vibrations from underground railway traffic based on a periodic finite element- boundary element formulation[J]. Journal of Sound and Vibration, 2006, 293(3-5): 645.

[11]Gupta S, Hussein M F M, Degrande G. A comparison of two numerical models for the prediction of vibrations from underground railway traffic[J]. Soil Dynamics and Earthquake Engineering, 2007, 27: 608.

[12]曾晨，孙宏磊，蔡袁强，等. 简谐荷载作用下饱和土体中圆形衬砌隧道三维动力响应分析[J]. 岩土力学,2014, 35(4): 1147.

ZENG Chen, SUN Honglei, CAI Yuanqiang,etal. Analysis of three-dimensional dynamic response of a circular lining tunnel in saturated soil to harmonic loading[J]. Rock and Soil Mechanics, 2014, 35(4): 1147.

[13]张曦，唐益群，周念清，等. 地铁振动荷载作用下隧道周围饱和软黏土动力响应研究[J]．土木工程学报，2007，40(2): 85.

ZHANG Xi, TANG Yiqun, ZHOU Nianqing,etal. Dynamic response of saturated soft clay around a subway tunnel under vibration load[J]. China Civil Engineering Journal, 2007, 40(2): 85.

[14]宫全美，徐勇，周顺华. 地铁运行荷载引起的隧道地基土动力响应分析[J]. 中国铁道科学, 2005, 26(5): 47.

GONG Quanmei, XU Yong, ZHOU Shunhua. Dynamic response analysis of tunnel foundation by vehicle vibration in metro[J]. China Railway Science, 2005, 26(5): 47.

[15]叶飞, 朱合华, 何川. 盾构隧道壁后注浆扩散模式及对管片的压力分析[J]. 岩土力学, 2009, 30(5): 1307.

YE Fei, ZHU Hehua, HE Chuan. Back-filled grouts diffusion model and its pressure to segments of shield tunnel[J]. Rock and Soil Mechanics, 2009, 30(5): 1307.

[16]张云,殷宗泽,徐永福. 盾构法隧道引起的地表变形分析[J]. 岩石力学与工程学报, 2002, 21(3): 388.

ZHANG Yun, YING Zongze，Xu Yongfu. Analysis on three dimensional ground surface deformations due to shield tunnel[J]. Journal of Rock Mechanics and Engineering, 2002, 21(3): 388.

Solution for Dynamic Stress of Saturated Soil Surrounding Shield Tunnel Based on Modified Shell-cylinder Model

DI Honggui, ZHOU Shunhua, SHAN Yao, HE Chao

(Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China)

To investigate the influence of grouting layer of shield tunnel on dynamic stresses of saturated soil under a harmonic loading, a modified shell-cylinder model is established. The lining and grouting layer of the shield tunnel are conceptualised as a double cylindrical shell and the saturated soil is conceptualised as a hollow cylinder with infinite radial extent. Based on the Flügge’s shell theory and Biot’s wave equations, the dynamic stresses of the soil induced by a stationary harmonic point load in the tunnel are analyzed. The results show that: The amplitude of radial normal stressτrrand pore-pressurePfof the soil beneath the grouting layer decreases with the increase of the longitudinal distance measured from the load point, and the amplitude of shear stressτrzof the soil increase firstly and then decrease with the increase of the longitudinal distance measured from the load point, which attenuate to zero as the longitudinal distance is approximately 3D(Dis the diameter of the tunnel). A worse permeability of the soil leads to a greater amplitude of radial normal stress and pore-pressure. However, when the soil permeability coefficientkis approximately smaller than 10-5m·s-1, the effect of the soil permeability on the amplitude of dynamic stresses is limited. The grouting layer can reduce the radial normal stress and pore-pressure of the surrounding soil (approximately 5%～8%); the magnitude of radial normal stress and pore-pressure of soil beneath the grouting layer decrease linearly with the increases of the thickness of grouting layer. However, the changes of the Young’s modulus of the grouting layer within a certain range of 50～650 MPa almost have no effect on the dynamic stresses of the saturated soil.

shield tunnel; saturated soil; grouting layer; dynamic stress

2015-12-08

国家自然科学基金(51478353)

狄宏规(1985—)，男，工学博士，主要研究方向为线路工程系统动力学.E-mail: dihongguila@126.com

周顺华(1964—)，男，工学博士，教授，博士生导师，主要研究方向为轨道交通结构设计理论与施工技术、线路工程系统动力学. E-mail: zhoushh@tongji.edu.cn

U 25

A