阻抗分析法在船舶结构动力响应分析中的应用研究

庞福振， 宋红宝， 缪旭弘， 王雪仁

(1.哈尔滨工程大学 船舶工程学院，哈尔滨　150001；2. 中国人民解放军92857部队,北京　100007)



阻抗分析法在船舶结构动力响应分析中的应用研究

庞福振1,2， 宋红宝1， 缪旭弘1,2， 王雪仁2

(1.哈尔滨工程大学 船舶工程学院，哈尔滨150001；2. 中国人民解放军92857部队,北京100007)

针对设备动力参数未知，设备基座振动加速度给定情况，提出阻抗分析法解决设备振动激励载荷下的船舶结构动力分析问题。基于理论分析，提出阻抗分析法，实现设备对基座的振动能量采取振动加速度激励作为输入，进而分析结构动力响应；通过舱段结构动力分析验证方法的有效性，并讨论不同加载方式对结构动力响应的影响规律，研究表明，该方法应用于结构声振分析是可行的，且加载方式对结构响应影响较大;在此基础上，将阻抗分析法应用于水下航行器水下声辐射研究，分析水下航行器声场周向分布规律。结果表明激励频率较低时水下航行器水下声场呈对称分布，随着频率提高，其对称性逐渐下降。

结构动力响应；阻抗；振动加速度；水下辐射噪声

在船舶结构动力分析中，如需准确预测结构动力响应，需要给出设备、结构的详细参数及设备激励力的详细数据，但是设备激励力数据较难测得，同时设备建模需花费大量时间，然而设备机脚振动速度及加速度数据较易测得。理论分析可知已知基座阻抗[1]及其振动情况可以求得其所受等效外力，保证系统的能量输入等效设备作用系统的输入能量，从而实现结构响应与实际设备系统响应相同。设备激励通过与其相连的基座向整个船体结构传播，保证基座等效受力可以使结构振动响应情况与实际情况相同，从而准确计算结构振动情况。现在国内外更多的是研究给定激励力作用下结构的动力响应情况，发展出了解析法、有限元法、边界元法、统计能量法等结构动力分析方法[2-7]。对于载荷以加速度或速度作为激励输入的研究还较少，当设备相关参数未知而仅已知基座加速度时，本文提出采用阻抗分析法应用于船舶结构的动力分析。

由阻抗理论可知，阻抗是系统动力性能的重要参数，其大小直接反应结构的对外作功(或外界对系统作功)能力，设备对船舶结构的振动能量也由结构的阻抗决定。理论分析可知，如结构的振动响应已知，则系统的输入能量直接由其阻抗决定。对于设备基座振动响应给定下的舰船结构动力分析而言，如能采用振动加速度或速度作为系统输入参数，则可简化结构分析，同时准确预报舰船结构的动力响应[8]。

首先通过理论分析说明阻抗分析法正确性，从等效载荷及等效能量输入角度进行讨论。通过算例验证阻抗分析法的有效性。通过将设备激励载荷直接以加速度或速度形式加载到设备连接基座上[9]，分析结构动力响应情况，同时分析基座不同加载方式对系统结构动力响应的影响。不同的施加方式，如激励以“机脚点载荷”或“基座面载荷”形式施加对结构动力分析结果会产生一定影响。在此基础上，将阻抗分析法应用于水下航行器水下声辐射研究，分析水下航行器声场周向分布规律。

1　阻抗分析法

通过分析图1中的“设备-基座”系统和“基座”系统的振动情况，将阻抗分析法引入到系统动力响应分析过程中。因为在推导以上两系统等效受力及等效能量输入过程中引入力阻抗概念，所以称该种分析方法为阻抗分析法。阻抗分析法是在系统阻抗一定情况下，通过使系统载荷作用处以特定振动情况运动，保证系统与实际情况下能量输入一致。

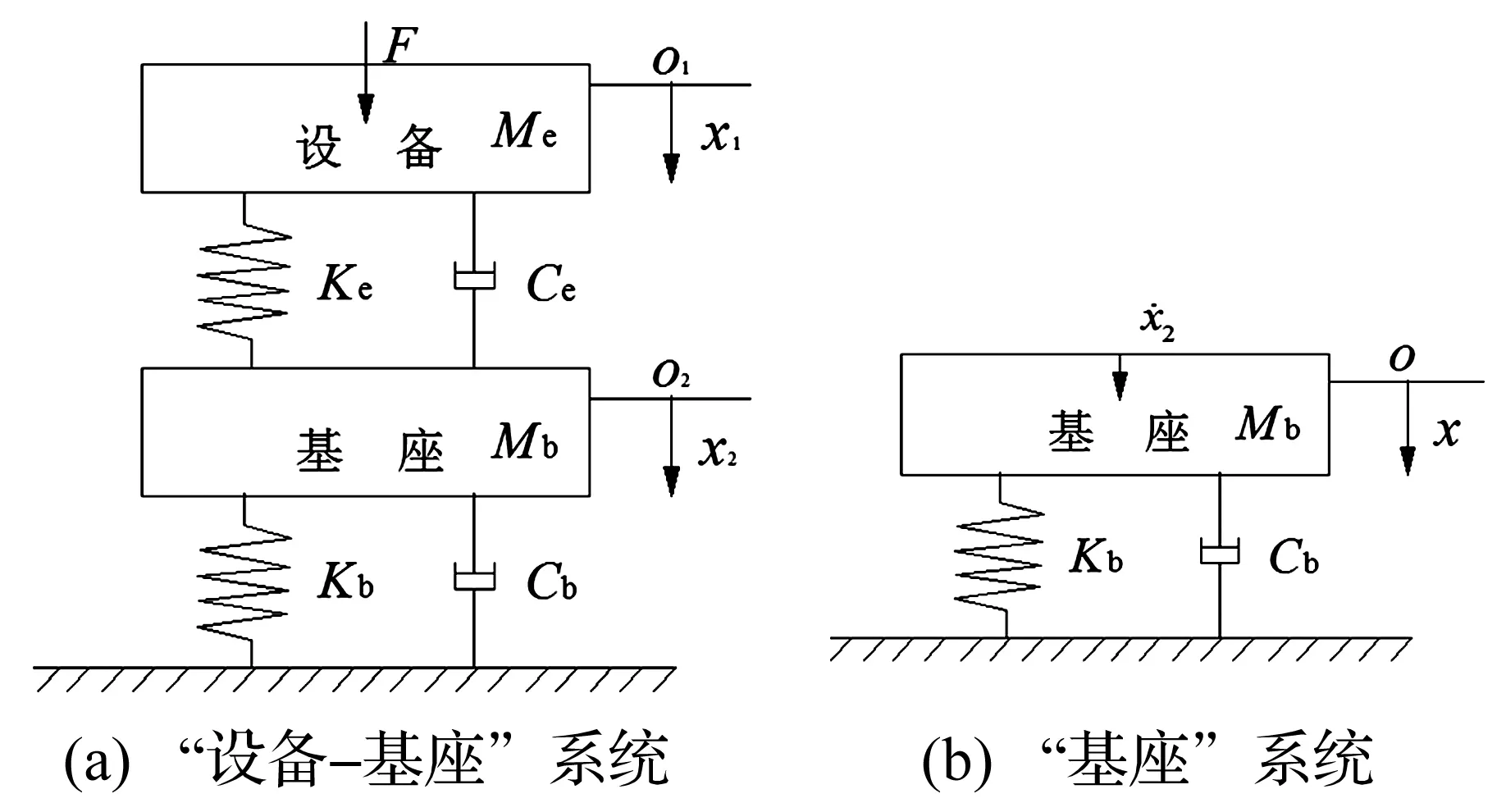
图1　系统模型图Fig. 1 The system model figure

由图1(a)可知，当有激励力F=F0ejωt作用于设备模型Me时，系统运动方程可表示为：

由此可以得到图1(a) “设备-基座”系统结构动力响应为：

(2)

式中：

图1(a)系统基座模型所受等效外力为:

(3)

将x2=D2ejωt/D代入上式得到：

F外=-ω2MbD2ejωt/D+

jCbωD2ejωt/D+KbD2ejωt/D

(4)

由图1(b)可知，其运动方程为：

(5)

式(5)可改写为：

(6)

求解式(6)得到外力与速度的关系为：

(7)

-ω2MbD2ejωt/D+

jCbωD2ejωt/D+KbD2ejωt/D

(8)

通过对比式(4)与式(8)，可得出两系统基座位置处受力相等。当结构以特定质点运动速度或加速度作为系统输入条件，可以实现系统间受力相等，证明阻抗分析法应用于结构动力响应分析的正确性。从而对于给定系统基座振动加速度或速度的情况，通过采用阻抗分析法将 “设备-基座”系统简化为“基座”系统，进而准确预报结构动力响应。

从系统能量输入角度考虑，当系统力阻抗一定时，系统能量输入情况如下：

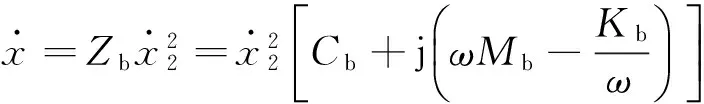
(9)

由此可知，当基座运动速度或加速度与“设备-基座”系统相同时，系统能量输入相同，从而证明阻抗分析法应用于结构动力分析的可行性。要保证两者系统响应相同，需要确保力阻抗Zb与实际情况相同，而力阻抗Zb与结构阻尼Cb、激励频率ω、结构质量Mb及结构刚度Kb有关，所以系统建模过程通过保证结构准确性来确保结构质量、刚度及阻尼与实际情况相同；同时由于结构阻抗与激励输入方式有关，如点阻抗与面阻抗不同，考虑激励作用方式的影响，确保激励加载与实际设备作用于基座情况相同。

通过理论分析可知：针对设备动力参数未知情况，当以设备机脚加速度作为输入条件作用于基座时，可保证结构响应与实际情况相一致，从而实现系统动力响应的准确分析。虽然公式推导是基于质点系动力学系统，但是对于质点-弹性体系统阻抗分析法同样有效。下面通过质点系动力学系统算例说明阻抗分析法有效性；并且通过另一算例验证阻抗分析法对于质点-弹性体系统同样适用，从而将阻抗分析法推广到复杂弹性体系统的结构动力响应分析中。

2　阻抗分析法有效性验证

2.1质点系动力学系统有效性验证

2.1.1质点系动力学模型简介

采用质点系动力学模型验证阻抗分析法的有效性，简化系统设备、基座模型为集中质量点，隔振装置简化为具有刚度及阻尼的弹簧。质点系统简化模型具体参数如下：设备、基座均简化为质量100 kg的质量点，系统所有弹簧刚度系数及阻尼系数为100 kN/m、1 kN·s/m，梁为0.02 m×0.02 m的矩形截面梁，长度为2 m，在基座质点及梁典型位置处设置考核点。考察图2(a)中弹簧上端作用恒力F=1 kN时，基座质点及梁考核点处的动力响应情况；当图2(b)中基座质点按图2(a)中其响应状态运动时，考察梁考核点处运动情况，并与图2(a)中相应考核点运动情况进行对比，模型计算频段为20～100 Hz，频率间隔Δf=5 Hz，验证阻抗分析法应用于质点系动力学系统有效性。

图2　质点系动力学系统模型Fig.2　The model of particle system

2.1.2数值计算结果分析

当图2(b)系统基座质点以图2(a)恒力作用下的基座质点运动状态运动时，考察梁典型考核点1#、2#、3#处结构响应情况，并将结果与图2(a)“设备-基座”系统对应考核点处响应情况进行对比。系统典型位置处动力响应对比结果见表1。

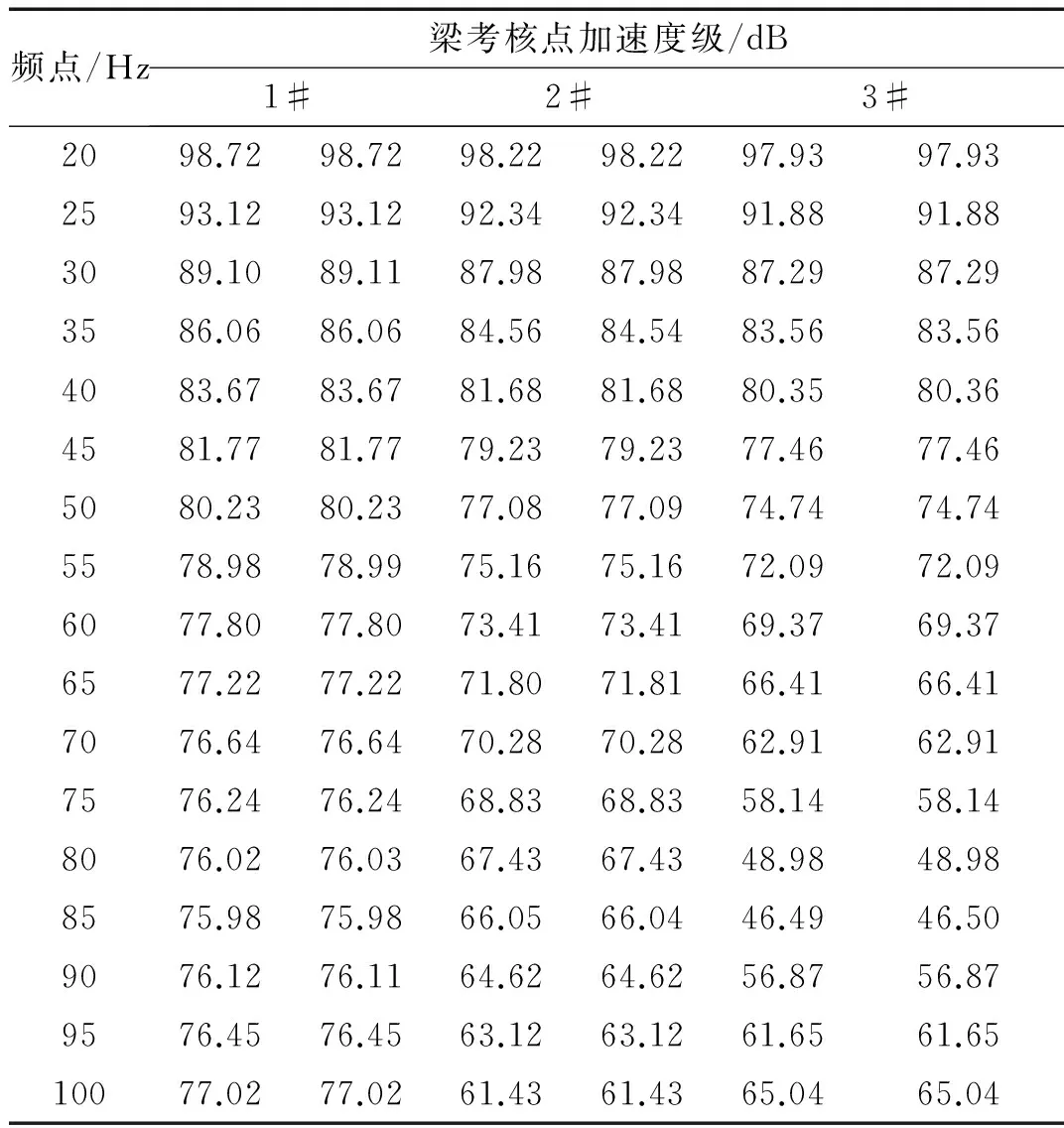
表1　梁考核测点加速度级

根据表中“设备-基座”和“基座”系统结构动力响应结果对比情况可知，两系统动力响应情况相一致。当以设备机脚加速度作为载荷输入条件作用于基座，可保证系统动力响应与原系统相一致，验证阻抗分析法应用于质点系动力学系统的有效性。

2.2弹性体系统有效性验证

2.2.1弹性体系统模型简介

上述研究从质点系统角度证明阻抗分析法应用于结构动力响应分析的正确性，下面将以具体算例说明阻抗分析法在弹性体系统结构动力分析中有效性。验证模型为一船舶舱段模型(见图3)，船舶壳体为R=2 m的半圆形结构，壳体厚度t=10 mm，船体舱段两端设置舱壁，船体结构内部设置间距L=500 mm、t=10 mm、h=200 mm肋骨；舱段尺寸为8 m×4 m×2.5 m的单壳结构，其壁面厚度为t=10 mm；两隔振器沿船体中心线对称分布于舱段对称中心处，隔振器刚度为k=10 kN/m；设备激振力采取F=100 N恒力垂直作用于设备面板中心位置；流场分内、外流场，内流场半径为4 m，外流场半径为7 m，流场外表面敷设无限元；计算频段为20～100 Hz，频率间隔Δf=5 Hz，结构损耗因子η=0.01。

图3　舱段结构及流场模型图Fig.3　The model of a ship cabin and fluid field

上述船舶舱段模型称“设备-基座”模型。为便于对比分析，以下不同加载情况所用模型均采用上述舱段模型，仅作部分修改(去掉设备、隔振装置)，阻抗分析模型中设备模型质量以集中质量点形式均布于设备机脚处，考虑设备质量对结构固有频率和模态的影响。其中舱段结构单元由2 475个四边形线性单元、356个梁单元组成，内、外流场分别由9 401个、20 683个六面体单元组成，模型共计32 915个单元。设备-隔振装置与基座连接处机脚情况见图4。

图4　隔振装置与基座连接图Fig.4　The vibration isolation device connection with the base figure

分别在舱段结构与流场设置振动及声压考核点，振动考核点沿舱段结构对称轴线布置于舱段肋骨处(见图5(a))，流场声压考核点设置于内外流场交界面对称剖面舱段首端、中间正下方处，声压考核点见图5(b)。

图5　结构振动及声辐射考核点Fig. 5 The testing points of structural vibration and acoustic radiation

2.2.2数值计算结果分析

在设备中心处施加F=100 N的恒力(如图3所示)，对“设备-基座”模型的动力响应情况进行分析，分别计算设备机脚4个接触点加速度级，同时计算舱段结构与流场典型考核位置的振动及声辐射频响曲线，其中设备机脚振动加速度数据见表2。

从表2可得到设备机脚各点加速度级相差不大的结论。将以机脚处施加载荷的模型取名为“机脚点载荷”模型，在基座面板上施加载荷的模型取名为“基座面载荷”模型。取上述4点加速度平均值，将其以运动边界条件施加到“机脚点载荷”、“基座面载荷”两模型上，两模型加载情况见图6。

表2　机脚测点加速度级

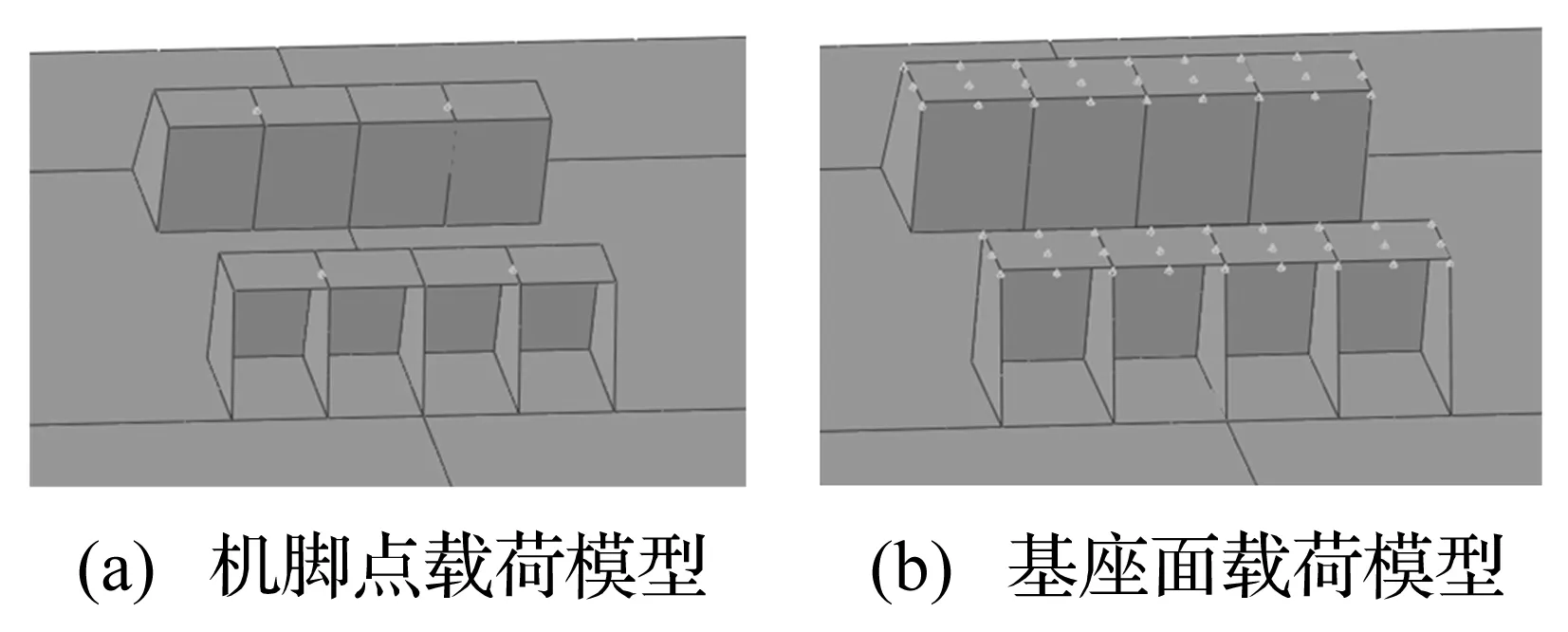
图6　基座激励加载方式Fig.6　The load way of base excitation

分别计算上述两种加载方式模型的典型考核部位振动及声辐射频响曲线，并且将考核点的计算结果与“设备-基座”模型对应位置的计算结果相比较。图7给出舱段考核点的振动频响曲线对比情况，图8给出流场考核点处的声辐射频响曲线对比情况。

图7　舱段典型考核点振动加速度曲线Fig.7　The acceleration level curve of a ship cabin

图7可得到“机脚点载荷”模型的舱段考核点振动加速度级与“设备-基座”模型的响应相一致，同时看出“基座面载荷”模型与 “设备-基座”模型结构振动响应结果相差较大，部分频点振动响应(如70 Hz频点)相差达到十几分贝。可以发现，当采用阻抗分析法激励输入方式时，结构动力响应与实际情况吻合，从而验证该方法有效性。

本文以软件与信息技术服务业A股上市公司为研究对象，选取2015年到2017年作为数据样本，筛选过程中，要将2015年证监会行业分类作为分析和研究的依据，并且有效剔除新上市的公司和数据不全的公司，与此同时，也要剔除经营异常的ST企业，经过筛选后得出66家公司2015年到2017年3年的基础数据。要建立对应的变量定义和取值量表。

图8　流场考核点辐射声压Fig.8　The acoustic radiation of fluid-field testing points

由图8可知，“机脚点载荷”模型的流场声辐射情况与“设备-基座”模型相一致，然而“基座面载荷”模型与“设备-基座”模型的响应情况相差较大。分析得到当激励输入方式与实际设备作用机脚位置相同时，流场的声辐射分布更符合实际情况。

图9给出了船舶舱段结构典型频点水下声辐射的分布情况，包括“设备-基座” 、“机脚点载荷”、“基座面载荷”三种模型水下声辐射分布对比图。

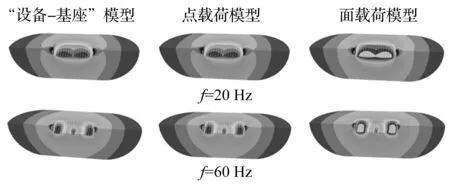
图9　舱段结构典型频点水下声辐射分布Fig.9　The underwater acoustic radiation distribution of a ship cabin

从图9可知,“设备-基座”模型与“机脚点载荷”模型的水下声辐射分布情况大致相同，与“基座面载荷”模型的水下声辐射分布情况相差较大。验证阻抗分析法在船舶结构水下振动声辐射研究中的有效性，同时说明激励输入方式对系统动力响应的影响。

3　阻抗分析法在水下航行器声学预报中的应用

3.1水下航行器声学计算模型简介

水下航行器模型系在BeTSSi-Sub模型[10]基础上对其结构进行局部修改(如内壳体与外壳体的结构形式及尺寸)得到，修改后模型见图10。

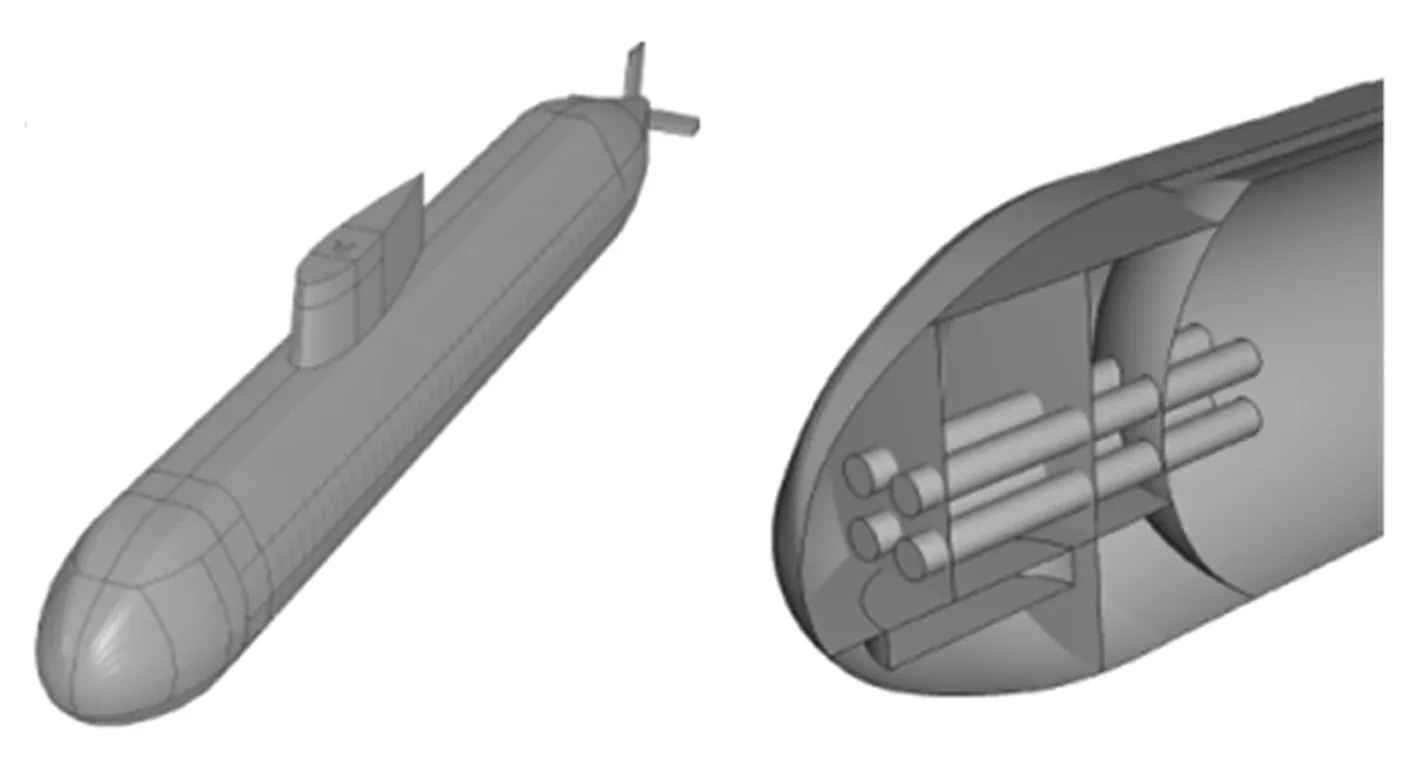
图10　水下航行器模型(BeTSSi-Sub)示意图Fig.10　Scheme of BeTSSi-Sub model

水下航行器推进电机基座处的振动加速度采用1 m/s2的恒定线谱载荷(见图11)，其作用频段为20～400 Hz，推进电机基座位于水下航行器对称中心靠近船尾处(即x/L=1/4)，分析水下航行器在推进电机激励载荷下的水下声辐射。

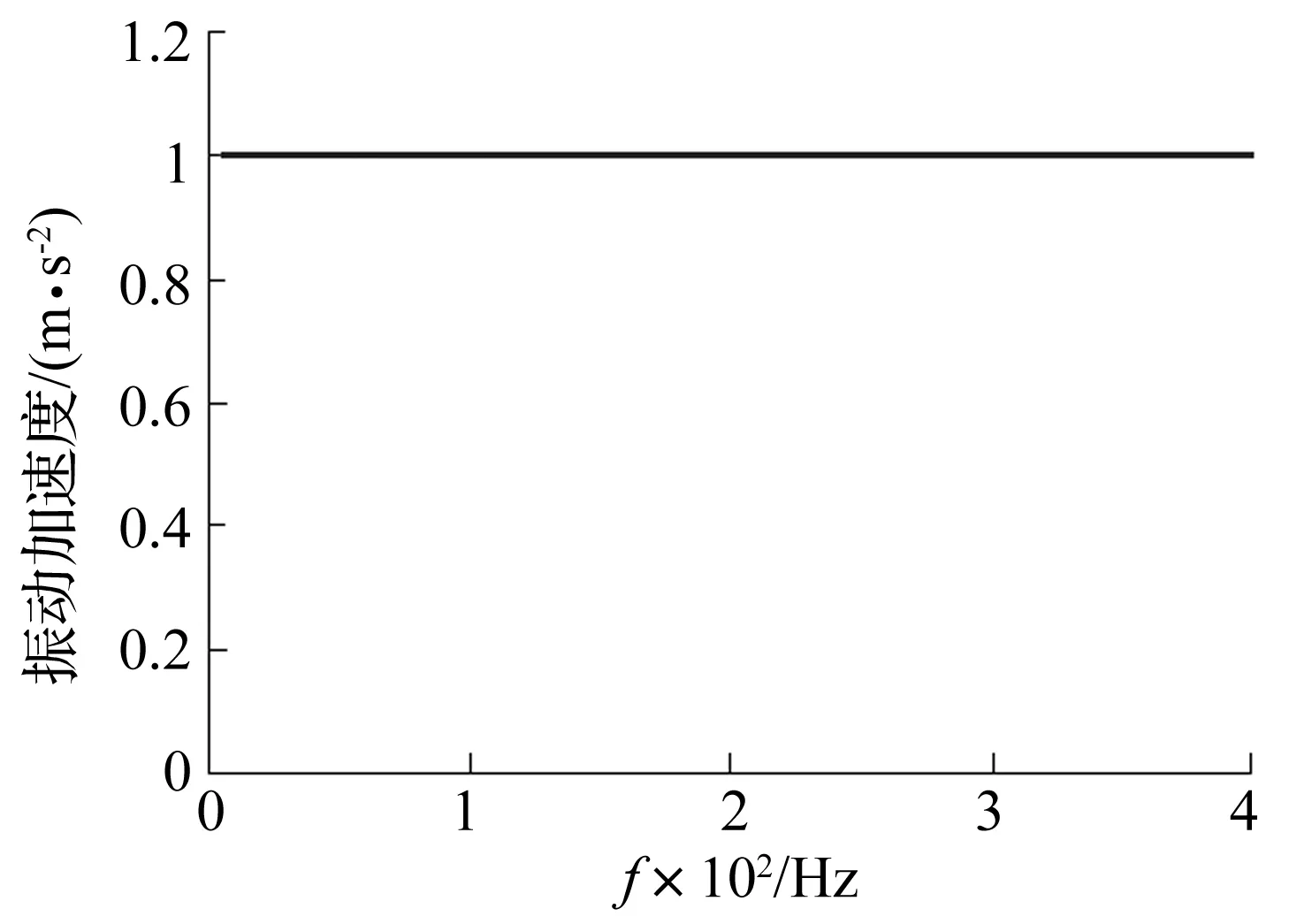
图11　水面船舶齿轮箱基座振动加速度曲线(线谱)Fig.11　Vibration acceleration of gearbox basement of a ship versus frequency

采用阻抗分析法将推进电机振动加速度激励施加到基座上，货物、压载及其它设备等采用质量点模型简化。水下航行器结构按BeTSSi-Sub简化模型构建，模型网格尺寸由20～400 Hz计算频段确定[11]。对于流场模型的建立，为降低计算规模，拟采用球柱组合型流场+无反射边界条件方式，流场域半径Rf按以下要求确定为:

Rf≥D/2+0.2λ=7/2+

0.2×1 500/20=18.25 m

(10)

式(10)为流场域的半球形流场及柱形流场域的最小半径[12]，为保障计算精度，本计算模型的流场域半径取为Rf= 22.5 m。

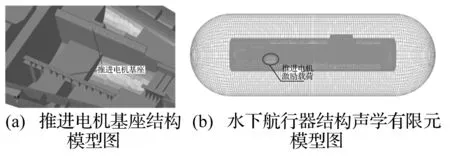
图12　水下航行器结构声学预报模型图Fig.12　Sub structural noise prediction model

3.2水下航行器声场周向分布

分析水下航行器声场沿横剖面的分布规律，图13～图15给出了x/L=1/4、x/L=1/2、x/L=3/4剖面(x/L的定义:x是以艇首为原点、艇尾方向为正方向的艇长坐标，L为艇长)、距水下航行器艇体中心R=8 m流场处的声压周向曲线。图15中横坐标为流场相对航行器对称中心线的周向角度，其角度方向定义：从船尾向船首看，左舷为90°，右舷为270°。纵坐标为无量纲声压Lp，其定义为：

(12)

式中：p0为基准声压，a0为基准加速度。

图13　x/L=1/4截面、R=8 m流场处声压周向分布曲线Fig.13　SPL of ship at cross section x/L=1/4, and R=8 m

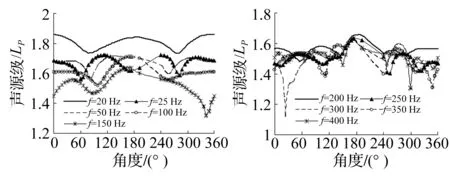
图14　x/L=1/2截面、R=8 m流场处声压周向分布曲线Fig.14　SPL of sub at cross section x/L=1/2, and R=8 m

图15　x/L=3/4截面、R=8 m流场处的声压周向分布曲线Fig. 15 SPL of sub at cross section x/L=3/4, and R=8 m

对比图13～图15可知，水下航行器的水下辐射声场分布同水面船舶存在一定差异：① 水下航行器水下辐射声场的对称性较水面船舶更为不均匀；② 水下航行器水下声场的离散度较水面船舶偏大。进一步分析表明，激励频率较低时水下航行器的水下声场沿横剖面大致呈对称分布于艇体对称中心两侧；但随着频率的提高，其对称性在逐渐下降，其水下声压幅值的变化也在迅速增大；当激励频率大于250 Hz时，其声场分布的对称性逐渐变差，其声辐射也主要集中于推进电机基座附近区域。

4　结　论

本文将阻抗分析法应用于设备动力参数未知情况的船舶结构动力响应分析。理论分析可知当激励作用位置的振动状态与实际情况一致，系统等效实际能量输入。针对船舶设备动力参数未知时，研究以设备机脚振动响应作为输入条件，进行结构动力分析的合理性。通过分析舱段结构验证方法的有效性。在此基础上，将阻抗分析法应用于水下航行器水下声辐射研究，通过研究得到如下结论：

(1) 通过船舶舱段模型验证了阻抗分析法应用于结构动力分析的有效性。通过理论分析说明了数学模型建立过程中应尽量保证结构质量、刚度及形式与实际情况相同。

(2) 设备激励载荷的输入方式对结构动力响应计算结果影响较大。计算过程中为确保结构动力分析的准确性，应保证数学模型激励的加载位置与实际结构受力位置相同。

(3) 水下航行器水下声场沿横剖面大致呈对称分布于艇体对称中心两侧；但随着频率的提高，其对称性在逐渐下降，其水下声压幅值的变化也在迅速增大；当激励频率大于250 Hz时，其声场分布的对称性逐渐变差，其声辐射也主要集中于推进电机基座附近区域。

[1] FULFORD R A, GIBBS B M. Structure-borne sound power and source characterization in multi-point-connected system part II: About mobility function and free velocities [J]. Journal of Sound and Vibration, 1997, 220(2): 203-224.

[2] 束长庚. 有限元解析法在船舶板架振动计算中的应用[J]. 舰船科学技术, 1979, 5(2): 39-56.

SHU Changgeng. Application of finite element analytical method in ship plate vibration calculation [J]. Chinese Journal of Ship Research, 1979, 5(2): 39-56.

[3] 邹春平, 陈端石, 华宏星. 船舶结构振动特性研究[J]. 船舶力学, 2003, 7(2): 102-115.

ZOU Chunping, CHEN Duanshi, HUA Hongxing. Study on structural vibration characteristics of ship [J]. Journal of Ship Mechanics, 2003, 7(2): 102-115.

[4] 庞福振,姚熊亮. 声学覆盖层对潜艇抗水下爆炸能力的影响研究[J]. 振动与冲击, 2011,30(4): 103-108.

PANG Fuzhen, YAO Xiongliang. Influence research of acoustic titles to the anti-underwater explosion capability of a submersible structure [J]. Journal of Vibration and Shock, 2011,30(4): 103-108.

[5] 缪旭弘, 钱德进. 基于ABAQUS声固耦合法的水下结构声辐射研究[J]. 船舶力学, 2009, 13(2): 319-323.

MIAO Xuhong, QIAN Dejin. Sound radiation of underwater structure based on coupled acoustic-structural analysis with ABAQUS[J]. Journal of Ship Mechanics, 2009, 13(2): 319-323.

[6] GUO Y P. Sound scattering by bulkheads in cylindrical shells [J]. Journal of the Acoustical Society of America,1994,95(5): 2550-2559.

[7] 崔晓兵, 季振林. 快速多极子边界元法预测船舶舱室噪声[J]. 噪声与振动控制, 2013, 32(6): 179-183.

CUI Xiaobing, JI Zhenlin. Fast multipole boundary element method for prediction of ship cabin’s noise [J]. Noise and Vibration Control, 2013, 32(6): 179-183.

[8] JANSSEN M H A. The use of an equivalent forces method for the experimental quantification of structural sound transmission in ship [J]. Journal of Sound and Vibration,1999,226(2):305-328.

[9] 庞福振. 船舶结构噪声截断模型数值预报方法研究[D]. 哈尔滨:哈尔滨工程大学, 2012.

[10] FIEDLER C, SCHNEIDER H G. “BeTSSi-sub—benchmark target strength simulation submarine,” technical report[R]. Forschungsanstalt Der Bundeswehr Für Wasserschall and Geophysik, Kiel, 2002.

[11] 邹春平. 船舶水下辐射噪声特性研究[J]. 船舶力学, 2004, 8(1)：112-124.

ZOU Chunping. Study on characteristics of ship underwater radiation noise [J]. Journal of Ship Mechanics,2004,8(1)：112-124.

[12] 商德江，何祚镛. 加肋双层圆柱壳振动声辐射数值计算分析[J].声学学报, 2001, 26(3): 193-201.

SHANG Dejiang, HE Zuoyong. The numerical analysis of sound and vibration from a ring-stiffened cylindrical double-shell by FEM and BEM [J]. Acta Acustica, 2001, 26(3): 193-201.

Impedance analysis method applied in underwater acoustic radiation analysis of ships

PANG Fuzhen1,2，SONG Hongbao1，MIAO Xuhong1,2，WANG Xueren2

(1. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China;2. Naval Academy of Armament, Beijing 100007, China)

For the case of equipments with locally unknown dynamic parameters and given under-chassis vibration acceleration, the impedance analysis method was proposed to solve the dynamic response of ships. The alternative energy input was achieved in accordance with the under-chassis vibration acceleration. The validity of the method was verified through the dynamic analysis of a ship compartment and the effects of different under-chassis loading ways were investigated. The results show that the method applied to the structural vibration analysis is feasible and the loading ways have a great influence on the dynamic structural responses. On this basis, the method was applied to study the submarine underwater acoustic radiation. The sound radiation distribution along the circumference was examined. The results show that with the increase of frequency, the inhomogeneity of the sub acoustic radiation is enhanced gradually.

structural dynamic response; impedance; vibration acceleration; underwater acoustic radiation

国家自然科学基金项目(51209052)；黑龙江省青年科学基金资助项目(QC2011C013)；上海交通大学海洋工程国家重点实验室基金(1307)；工信部高技术船舶项目;中央高校基本科研业务费资助项目(HEUCF140117);国防预研项目(4010403010103);中国博士后基金(2014M552661)

2015-06-10修改稿收到日期：2015-09-06

庞福振 男，博士，副教授，1980年生

宋红宝 男，硕士，1990年生

TH212；TH213.3

A DOI:10.13465/j.cnki.jvs.2016.14.003