不完全量测的变维容积卡尔曼滤波算法
张虎龙
(中国飞行试验研究院,陕西 西安 710089)
不完全量测的变维容积卡尔曼滤波算法
张虎龙
(中国飞行试验研究院,陕西 西安 710089)
针对不完全量测情况下的机动目标跟踪问题,提出一种变维容积卡尔曼滤波算法。首先,根据系统状态空间模型结构采用Kalman滤波-容积Kalman滤波(KF-CKF)为基本滤波器。其次,通过计算不完全量测的一阶矩和二阶统计矩,将不完全量测滤波问题转化为确定量测滤波问题,并导出相应的状态估计方法。最后,将其与变维滤波技术相结合,提出不完全量测下的变维CKF算法。计算机仿真实验表明:新算法具有很好的估计准确度,在机动目标跟踪应用中有着良好的应用前景。
目标跟踪;变维滤波;容积卡尔曼滤波;不完全量测
0 引 言
目标跟踪技术广泛应用于战场监控、预警、火力控制以及空中交通管理等军事和民用领域[1-4]。Kalman滤波作为一种线性系统的状态估计方法无法直接应用到具有非线性系统特征的目标跟踪背景中。为解决这一问题,人们在Kalman滤波框架下发展出一系列非线性滤波器,如扩展Kalman滤波(EKF)、无迹Kalman滤波(UKF)[5]和容积Kalman滤波(CKF)[6];其中,CKF由于其优越的性能已广泛应用于目标跟踪领域。需要注意的是,这些非线性滤波方法必须基于有效的状态空间模型。对于机动目标而言,使用单一模型很难准确描述目标状态在机动下的变化过程。针对这一问题,Bar-Shalom[1]提出了变维滤波算法,通过使用多个状态模型全面描述系统,大大提高了机动目标的跟踪性能[7-8]。由于目标高机动性、恶劣气象环境影响以及观测设备的间歇性故障等因素共同作用,时常出现不完全量测现象[9]。文献[10]利用一个取值为0或1且服从Bernoulli分布的随机变量建立了测量数据丢失现象的数学模型。文献[11]假设不确定量测模型中的Bernoulli随机变量与系统状态和噪声变量相互独立,并提出了相应的改进EKF和UKF算法。该方法仍然无法克服单一模型用于机动目标跟踪的不足。
本文针对不完全量测下机动目标的跟踪问题,以CKF为基础滤波器,结合变维滤波技术提出了一种不完全量测概率恒定已知(即已知恒虚警率)的变维CKF跟踪算法,提高了机动目标跟踪准确度。
1 目标运动模型
目标的运动模型包括非机动模型和机动模型。对于非机动模型,选取匀速直线运动模型,其状态方程[1-2]为
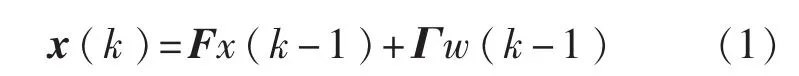
式中x(k)=[x1(k),ν1(k),x2(k),ν2(k)]T为目标状态,其中x1(k)和x2(k)分别为东向和北向的位置分量,ν1(k)和ν2(k)分别是相应的速度分量;F为状态转移矩阵;Γ为噪声驱动矩阵;过程噪声w(k)是均值为零方差为Q(k)的高斯白噪声,各参数取值如下:
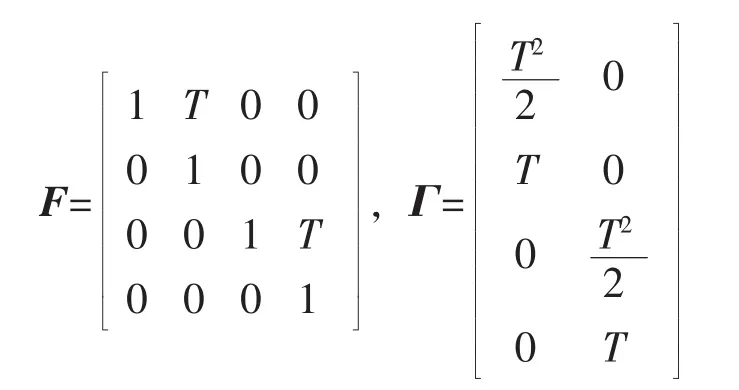
对于机动模型,假设目标作匀加速直线运动,其状态方程[2]为

式中,上标m表示机动模型;目标状态xm(k)=[x1(k),ν1(k),x2(k),ν2(k),a1(k),a2(k)]T,其中a1(k)和a2(k)分别为东向和北向的加速度分量,其他参数含义与非机动模型一致;过程噪声wm(k)是均值为零方差为Qm(k)的高斯白噪声。相应参数的取值如下:

假设一部雷达对目标进行跟踪,具有不完全量测的测量方程[11]表示为
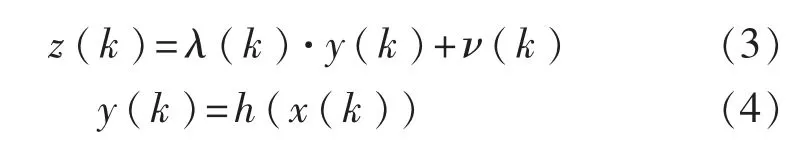
式中z(k)为k时刻的实际测量值;y(k)为k时刻的真实测量值;测量噪声ν(k)是均值为零方差为R(k)的高斯白噪声;λ(k)是一个Bernoulli随机变量,λ(k)=1和λ(k)=0分别表示量测数据正常和量测数据丢包。假设量测数据正常的概率满足P{λ(k)=1}=p,则量测丢包的概率(即虚警概率)为1-p。
假设目标初始状态x(0)均值为x0,方差为P0。目标状态、λ(k)、w(k)和ν(k)相互独立。
显然,非机动模型和机动模型两者都具有相同的测量方程,即z(k)=zm(k)。
2 确定量测的机动目标跟踪算法
本节首先考虑无量测丢包(即认为λ(k)=1恒成立)情况下的机动目标跟踪问题。由于目标的状态方程与测量方程具有线性-非线性结构,因此主滤波器采用KF-CKF的滤波器结构,即利用KF进行状态预测,然后采用CKF进行测量更新。利用非机动状态模型(1)和测量方程(3)可得KF-CKF算法的执行步骤如下(算法1,记作KF-CKF-NMT):
1)预测过程[1]:
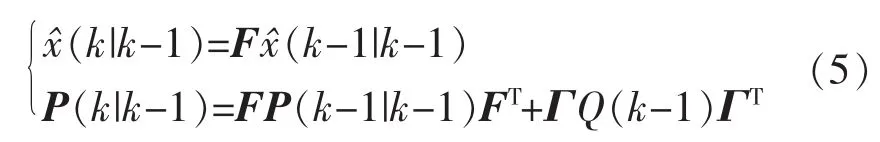
2)更新过程[6]:
①计算容积点

式中i=0,1,…,2nx(nx为状态向量维数);S(k|k-1)为P(k|k-1)的Cholesky分解因子;点集{ξi}的定义参见文献[6]。
②计算传播后的容积点

③测量预测

④计算新息协方差阵

⑤计算互协方差阵

⑥估计状态及其协方差阵
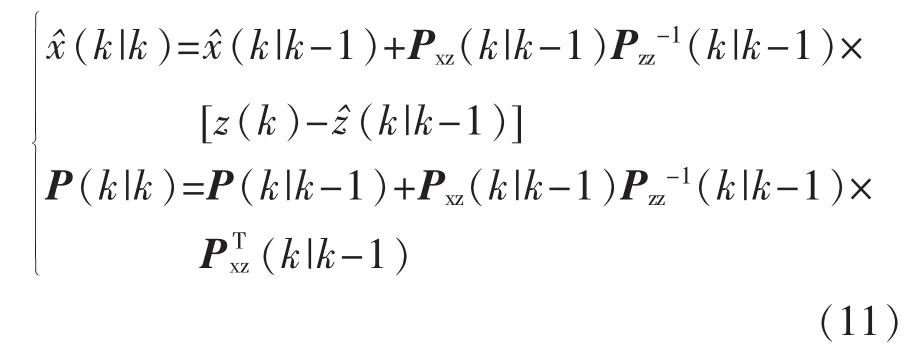
算法1采用了标准的KF进行状态预测,避免了在预测过程中采用CKF进行数值逼近,简化了运算,并保证估计精度。对于机动模型而言,将算法KFCKF-NMT中的参数分别替换为机动模型的对应参数即可(此时的算法记作KF-CKF-MT)。需要注意的是,非机动模型和机动模型的状态维数nx分别为4和6。
变维滤波基本思想是:当检测到机动发生,立即切换到机动模型进行跟踪,退出机动时退回到非机动模型跟踪。下面介绍变维滤波的机动检测方法,假设滤波器开始工作于非机动模式。
1)非机动模型切换到机动模型
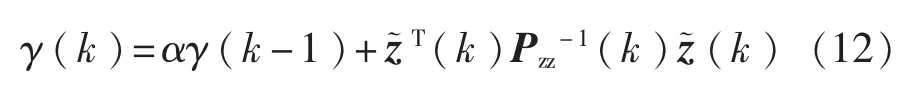
定义检测机动的有效窗口长度为

其中α为衰减因子,且有0<α<1。
设T1为机动检测门限。若γ(k)≥T1,则认为目标在k-Δ-1开始有一恒定的加速度加入,这时目标模型应由非机动模型转向机动模型。
2)机动模型切换到非机动模型
由机动模型退回非机动模型的检测方法是检测加速度估计值是否有统计显著性意义。令加速度估计的显著性检测统计量为

Pam(k/k)——协方差矩阵的对应块。
设T2为退出机动的检测门限。若γa(k)<T2,则加速度估计无显著性意义,滤波器切换回非机动模型。
将KF-CKF与变维滤波相结合,便可得到正常量测下的机动目标跟踪算法(记作VD-KF-CKF),其执行过程总结如下:
1)滤波初始化,设置系统初值x0、P0和机动检测门限值T1、T2,衰减因子α。
2)采用KF-CKF-NMT进行目标跟踪。
3)启动机动检测器,利用式(12)计算参数γ(k),并判断γ(k)≥T1是否成立,若是则转到步骤4);若否,则返回步骤2)。
4)采用KF-CKF-MT进行目标跟踪。
5)利用式(14)计算γa(k),并判断γa(k)<T2是否成立,若是则转到步骤2);若否,则执行步骤4)。
3 不完全量测的机动目标跟踪算法
传统的不完全量测处理方法是野值剔除法,该方法的处理结果易受残差检测门限的影响。门限值选取过大,则检测结果存伪的可能性大;反之,则去真的可能性过大。为避免这一问题,本文利用下述引理将不完全量测滤波问题转化为确定信息的滤波问题。
引理1[11]:已知n维随机向量x,m维随机向量y=h(x)(h为m维的向量函数)和ν(其均值为零,方差为R),Bernoulli随机变量λ(其期望为p)。假设x,ν,λ相互独立,则随机向量z=λy+ν的一阶矩E(z)和二阶矩Cov(z)、Cov(x,z)满足:
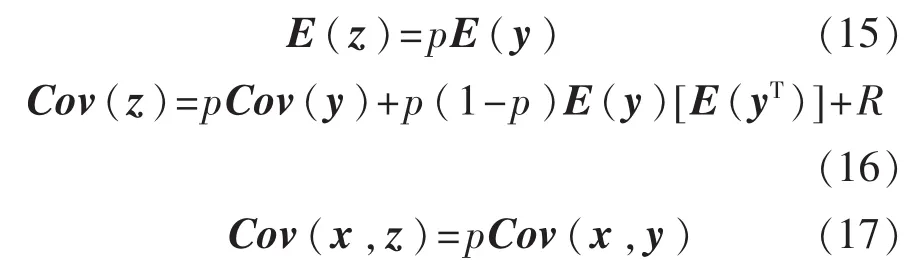
引理1揭示了两个随机变量z和y在引入Bernoulli随机变量后,其部分一阶矩和二阶矩的对应关系。根据引理1,结合非机动状态模型,易得不完全量测下的KF-CKF滤波方法,即定理1。
定理1:考虑式(1)、式(3)和式(4)所述的目标跟踪系统,在KF-CKF滤波结构下,其目标状态的估计方法(算法2,记作KF-CKF-UM-NMT)可按如下步骤计算:
1)预测过程
利用式(5)计算x^(k|k-1)和P(k|k-1)。
2)更新过程
①利用式(6)计算容积点xi(k|k-1)。
②计算传播后的容积点

③测量预测

④计算新息协方差阵
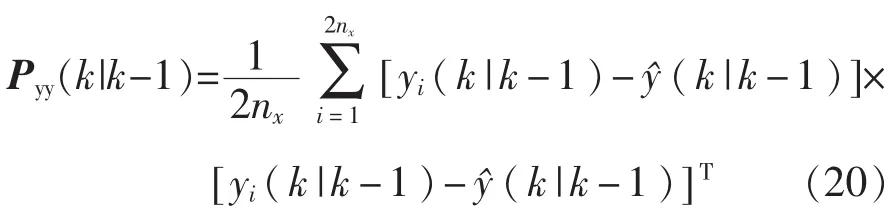
⑤计算互协方差阵
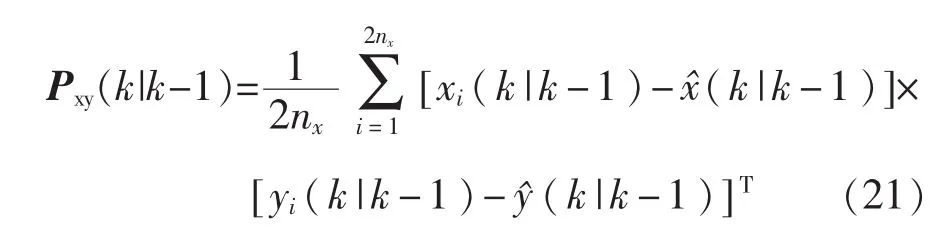
⑥估计状态及其协方差阵

证明:由于不确定量测仅影响量测更新过程,因此状态预测过程与算法1相同。在Kalman滤波框架下,状态估计及其误差协方差阵[1]可表示为
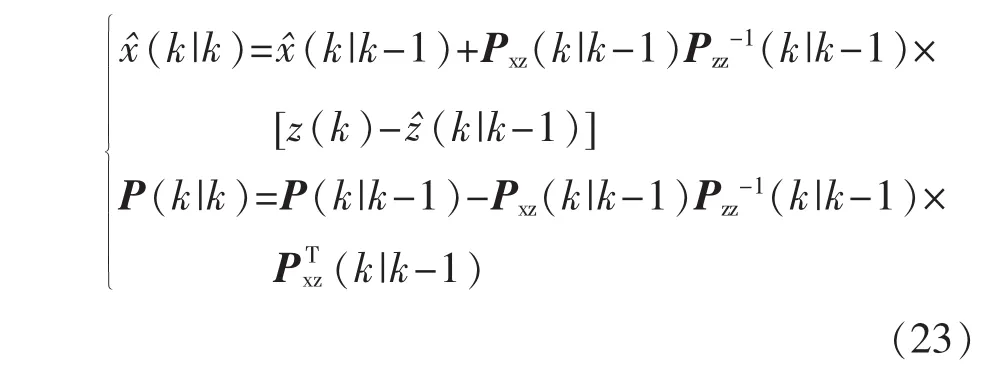
其中参考测量方程(3)和(4),利用引理1有:
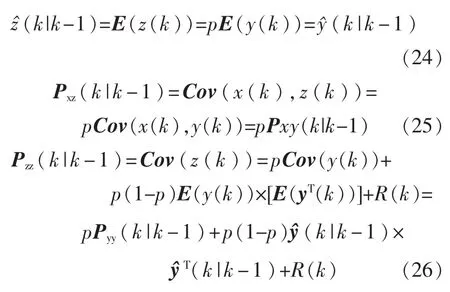
式(24)~式(26)中,基于测量真值y(k)的测量更新过程可由标准的CKF获得,即式(18)~式(21)所述。
将式(24)和式(25)代入式(23)可得式(22)。
定理证毕!
算法2计算Pyy(k|k-1)时没有噪声方差R(k),这是因为测量真值模型中不含噪声项。将算法KFCKF-UM-NMT中的参数分别替换为机动模型的对应参数即可获得机动模型的目标状态估计方法(此时的算法记作KF-CKF-UM-MT)。
显然,将VD-KF-CKF算法中的基础滤波器KFCKF-NM和KF-CKF-NM分别替换为KF-CKFUM-NMT和KF-CKF-UM-MT,即可得到不完全量测下的机动目标跟踪算法(记作VD-KF-CKF-UM),在此不再赘述具体步骤。
4 仿真实例
假定目标在二维平面内运动,在0~200s沿着y轴作匀速直线运动,运动速度为20m/s,目标的起始位置为(5000m,10000m);在201~300s向x轴方向做了1次机动,加速度为a1=-a3=0.08m/s2,完成慢转弯后加速度降为零,做匀速直线运动;从500 s开始第2次机动,加速度为-a1=a3=0.5m/s2,在600 s结束转弯加速度降为零,然后做匀速直线运动。
假设有一部位于坐标原点的雷达对该运动目标进行跟踪,测量距离r(k)和方位角θ(k),则相应的测量方程为

其中,雷测距标准差σr=10 m,方位角测量标准差为σθ=0.5°。
雷达扫描周期T=1s,仿真时长为800s,虚警概率为0.15,加权衰减因子α=0.85,机动检测门限T1=25,退出机动的检测门限T2=10;从第15s开始激活机动检测器。
采用文献[12]中的位置分量和速度分量的平方根误差SEP(k)、SEV(k)和均值误差MSEP、MSEV 4个误差指标对本文提出的算法进行性能评价。仿真结果由图1~图3给出,算法的MSEP和MSEV分别为19.896 0 m、0.648 1 m/s。
从图1可以看出,本文提出的方法能有效跟踪机动目标,具有较好的跟踪精度。但图2和图3也反映出当目标机动时,会出现较大的跟踪误差。此时可通过调整变维滤波器中的有关参数改善性能。
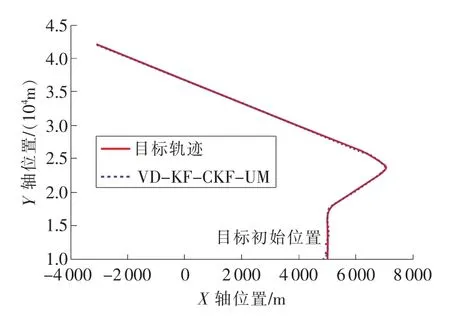
图1 机动目标跟踪曲线

图2 平方根误差曲线(位置分量)

图3 平方根误差曲线(速度分量)
5 结束语
本文针对机动目标跟踪过程中易出现的量测丢失(虚警)和滤波精度效果差等问题,提出一种不完全量测下的机动目标跟踪算法。首先,将不完全量测的状态估计问题转化为确定量测的估计问题,并利用KF-CKF设计滤波算法。然后,结合变维滤波的思想,推导出不完全量测下基于变维CKF的跟踪方法。本文的研究结果是在虚警概率恒定已知的条件下得到的,进一步的研究工作可考虑未知虚警概率的机动目标跟踪问题,相关研究成果有助于推动不确定信息滤波技术的发展,也更符合实际目标跟踪的应用背景。
[1]BAR S Y,BIRMIWAL K.Variable dimension filter for maneuvering target tracking[J].IEEE Transactions on Aerospace and Electronic Systems,1982,18(5):621-629.
[2]LIXR,JILKOV V P.Survey of maneuvering target tracking Part I:dynamic models[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1333-1364.
[3]鲁永杰,王思明.一种改进的运动目标跟踪方法[J].中国测试,2015,41(7):95-98.
[4]LAN J,LI X R.Tracking of maneuvering non-ellipsoidal extended object or target group using random matrix[J].IEEE Transactions on Signal Processing,2014,62(9):2450-2463.
[5]JULIERSJ,JEFFREYK U,DURRANTT H F.A new method for the nonlinear transformation of means and covariances in filters and estimators[J].IEEE Transactions on Automatic Control,2000,45(3):477-482.
[6]ARASARATNAM I,HAYKIN S.Cubature kalman filters[J].IEEE Transactions on Automatic Control,2009,54(6):1254-1269.
[7]CLOUTIER J R,LIN C F,YANG C.Enhanced variable dimension filter for measuring target tracking[J]. IEEE Transac tions on Aerospace and Electronic Systems,1993,29(3):786-796.
[8]余小游,高亭亭,孙广富,等.卫星导航弱信号的变维卡尔曼滤波跟踪算法[J].国防科技大学学报,2015,37(3):56-60.
[9]CABALLERO-ÁGUILAR,HERMOSO-CARAZOA,LINARES-PÉéREZ J.Covariance-based estimation algorithms in networked systems with mixed uncertainties in the observations[J].Signal Processing,2014,94(1):163-173.
[10]WANG Z,YANG F,HO D W C,et al.Robust H∞filtering for stochastic time-delay system with missing measurements[J].IEEE Transac-tions on Signal Processing,2006,54(7):2579-2587.
[11]HERMOSO-CARAZO A,LINARES-PÉREZ J.Different approaches for state filtering in nonlinear systems with uncertainobservations[J].AppliedMathematicsand Computation,2007,187(2):708-724.
[12]管冰蕾,汤显峰,葛泉波.未知测量噪声方差的平方根高阶容积Kalman滤波[J].计算机应用研究,2015,32(9):2626-2629.
(编辑:莫婕)
Variable dimension cubature kalman filter algorithm with incomplete measurements
ZHANG Hulong
(Chinese Flight Test Establishment,Xi’an 710089,China)
Aiming at the problem of maneuvering target tracking with incomplete measurements,a variable dimension cubature Kalman filter algorithm is proposed.Firstly,the Kalman filtercubature Kalman filter(KF-CKF)is adopted as a basic filter according to the state space model of tracking system.Secondly,by calculating the first and second-order statistical moments of the incomplete measurements,the state filtering with incomplete measurements is converted into the state estimating with complete measurements.Then,the corresponding state estimation method is derived.Finally,combining with variable dimension filter technology,a variable dimension CKF algorithm is presented.Computer simulations show that the new algorithm has good estimation accuracy and great application prospect of maneuvering target tracking.
target tracking;variable dimension filter;cubature Kalman filter;incomplete measurement
A
1674-5124(2016)06-0112-05
10.11857/j.issn.1674-5124.2016.06.024
2015-12-10;
2016-02-10
张虎龙(1979-),男,湖南岳阳市人,高级工程师,研究方向为光电测试、信息融合、目标跟踪技术等。

