行星轮系的有限元分析

贺声阳

（沈阳航空航天大学 工程训练中心，沈阳 110136）

行星轮系的有限元分析

贺声阳

（沈阳航空航天大学 工程训练中心，沈阳 110136）

初步确定行星轮系的各元件参数，建立行星轮系统的三维系统模型，对行星轮系进行有限元的静力分析和模态分析，得到了行星轮系的应力分布情况及振动频率和对应振型，验证了齿轮参数设置的正确性，为进一步进行行星轮系的优化设计提供了理论依据。

行星轮系；有限元；分析

1　行星轮系的建立

行星齿轮的传动，齿数的选择必须满足以下条件：

1）满足传动比条件，保证满足给定传动比的要求。

2）满足邻接条件，由多个行星轮均匀对称的布置在太阳轮和内齿圈之间，设计中必须保证相邻两行星轮齿顶不得互相碰撞。

3）满足同心条件，由太阳轮和行星轮组成的所有啮合副实际中心距必须相等。

4）满足装配条件，行星轮能均匀装入并保证与太阳轮正确啮合所具备的齿数关系和切齿要求。

在满足以上条件的前提下，经计算初步选定太阳轮、行星轮、内齿圈的模数、齿数、及变位系数等参数，如表1所示。

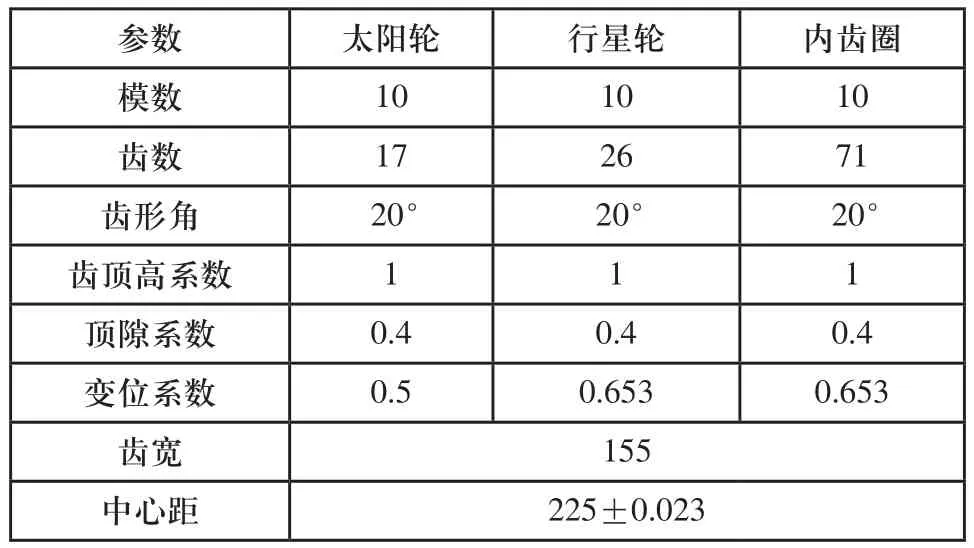
表1　行星轮系齿轮参数表

在Pro/E中建立太阳轮、行星轮、内齿圈、行星架的三维模型，进行组件的装配，在机构模块中定义太阳轮-行星轮，行星轮-内齿圈为齿轮副连接（如图1、图2所示），进行运动学检查，保证系统运行顺畅。

图1　行星轮系实体模型

图2　定义齿轮副连接

2　行星轮系的静力分析

将三维模型导入有限元分析软件A N S Y SWorkbench。选取太阳轮与行星轮的齿面进行接触定义，定义为不分离的接触形式；选取行星轮的齿面与内齿圈的齿面进行接触定义，定义为不分离的接触形式（如图3、图4所示）。

对行星轮系有限元模型施加约束，内齿圈施加固定约束，行星轮施加圆柱面约束（径向及轴向固定、切向自由），太阳轮施加圆柱面约束（轴向固定、径向和切向自由）。对太阳轮施加26465000Nm的转矩（如图5所示）。

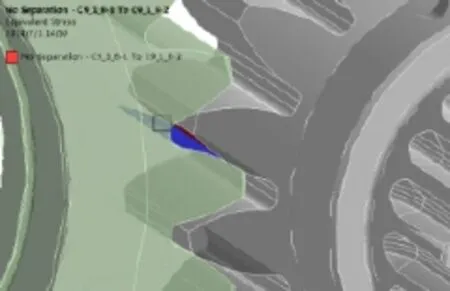
图3　太阳轮与行星轮接触

图4　行星轮与内齿圈接触

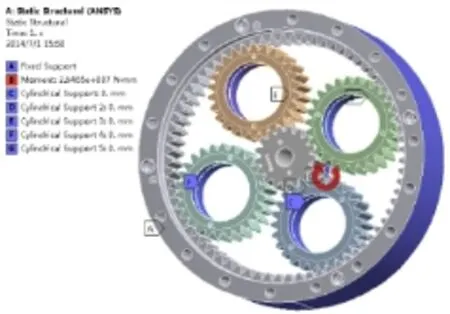
图5　施加载荷和约束

通过有限元软件ANSYS-Workbench求解计算后，得到行星轮系有限元模型在外加转矩的作用下的位移云图和应力云图（如图6、图7所示）。

图6　位移云图

图7　应力云图

从图中可以看出最大位移发生在太阳轮的连接花键最外边缘，最大位移值为0.50362mm；最大应力值出现在太阳轮齿根部，最大应力值为415.39MPa。内齿圈处的最大应力值为167.32Mpa，行星轮处的最大应力值为302.01MPa。

3　行星轮系的模态分析

模态分析是用来获得一个结构的固有频率和振型，在解决更为复杂的动态问题之前，通常先进行模态分析。在此模态分析中，假设结构是线性的。

通过模态分析，得到前六阶的固有频率，如表2所示。

表2　行星轮系的前六阶固有频率

对应的振型是太阳轮的摆动及四个行星轮的扭转振动，对应的振型如图8所示。

【】【】

图8　前六阶固有频率对应的振型

通过振动动画显示，行星轮的振动对整个系统的影响较大。

4　结论

本文应用有限元分析软件ANSYS-Workbench，对行星轮系进行了静力分析、模态分析，得到了行星轮系的最大应力值及位移值。最大应力值出现在太阳轮处，在整个行星轮系中需要加强太阳轮的强度设计，使其满足设计要求，以保证整个行星系统的可靠运行。模态分析显示行星轮的振动对整个系统的影响较大，在设计及使用中需避免行星轮的过大振动。

［1］ 孙横，陈作模，葛文杰.机械原理［M］.北京:高等教育出版社，2006.

［2］ 邓凡平.ANSYS10.0有限元分析自学手册［K］.北京:人民邮电出版社，2007.

［3］ 胡来瑢.行星传动设计与计算［M］.北京:煤炭工业出版社，1997.

The finite element analysis of planetary system

HE Sheng-yang

机器人技术

TH132.425

A

1009-0134（2016）09-0035-03

2016-06-06

贺声阳（1980 -），男，辽宁抚顺人，工程师，硕士，研究方向为机械设计及数控技术。