正则化方法在结构模型修正中的应用研究*
李英超, 王树青, 张 敏
(1.鲁东大学土木工程学院,山东 烟台 264025; 2.中国海洋大学工程学院,山东 青岛 266100)
研究简报
正则化方法在结构模型修正中的应用研究*
李英超1, 王树青2, 张敏2
(1.鲁东大学土木工程学院,山东 烟台 264025; 2.中国海洋大学工程学院,山东 青岛 266100)
大型结构的模型修正求解问题多呈现不同程度的病态,实测数据的微小误差都有可能造成求解的失效。该文研究了测量噪声影响下模型修正病态系统的求解问题。首先,介绍了结构模型修正的求解问题以及数学上常用的正则化方法;然后,通过一悬臂梁模型数值算例探讨了截断奇异值分解正则化方法和“L”曲线法在结构模型修正求解中的适用性。结果显示,适当的正则化可以有效的解决模型修正病态系统的求解问题;另外,该方法对于部分满足离散Picard条件的模型修正方程同样适用。最后,通过一导管架平台物理模型试验对该正则化方法的实用性进行了验证。
模型修正; 病态;正则化;导管架平台
引用格式:李英超, 王树青, 张敏. 正则化方法在结构模型修正中的应用研究[J]. 中国海洋大学学报(自然科学版), 2016, 46(9): 107-115.
LI Ying-Chao, WANG Shu-Qing, ZHANG Min. Study on the application of regularization method in structural model updating[J]. Periodical of Ocean University of China, 2016, 46(9): 107-115.
一个反应实际的有限元模型是进行结构计算分析和安全评估的基础。然而在实际工程中,有限元模型与实际结构之间往往存在差异,解决这一问题的常用方法是模型修正[1]。
近年来,随着模型修正方法的日趋成熟,学者和工程师们将其应用到了桥梁[2-3]、房屋[4]和海洋平台[5-7]等土木工程领域。然而,大量研究表明,简单的将现有的模型修正方法应用到海洋平台、桥梁等复杂的结构上,效果并不理想。究其原因:从技术本身来讲,动力模型修正是结构动力学的反问题,修正方程常呈现病态,实测数据的微小误差将会引起解的“振荡”;另外模型修正方程的解往往具有非唯一性,此时只能通过估计方法给出最优解,估计误差的大小与方程的病态性以及实测信息的数量和精度直接相关[8]。从工程角度来讲,海洋平台等三维结构在建模中通常需要进行大量的简化,实际结构参数的不确定性较多;另外,受工作环境限制,实测信息量非常有限,且受噪声污染较严重。因此,研究实测数据含噪声情况下模型修正病态方程组的求解问题,对于模型修正方法推向工程应用具有重要的意义。
上述病态方程组的求解问题在数学领域并不罕见,常用的手段是正则化方法。最早的正则化方法由Tikhonov[9]提出,通过正则化参数的选择,使得正则解在最小二乘解和最小范数解之间取得平衡,从而控制解的振荡和修正的拟合程度。目前最常用的正则化方法主要依据矩阵的奇异值分解(SVD)技术,如截断奇异值分解(TSVD)方法[10-12]。文献[8]对各种正则化方法进行了较系统深入的研究,针对不同规模的病态系统提出了适用的正则化方法,并指出利用正则化方法求解不适定问题的关键是正则化参数的选择,这一过程通常需要借助一些数学统计手段,如Morozov偏差准则,广义交叉检验法, “L”曲线法等,这些方法均需要进行大量的试算。
正则化方法尽管在理论上比较完善,但在模型修正的实际应用中却仍然存在一些问题,如对于不同问题,同一算法表现出的收敛性却不同,很难用一个通用的方法解决不适定问题[13]。
本文将数学上常用的TSVD正则化方法和“L”曲线法引入到结构模型修正线性方程组的求解中,然后通过一悬臂梁数值算例来探讨该方法的适用性,最后通过一海洋平台物理模型试验对该方法的实用性作进一步验证。研究中,模型修正线性方程组的构建方法采用文献[14]提出的交叉模型交叉模态方法,受篇幅限制,不再对该方法进行详细介绍。
1 模型修正求解问题
现有的模型修正方法,虽然思路不尽相同,但大多可归结为线性方程组
Ax=b
(1)
根据m和n的大小关系,式(1)所示线性方程组有三种情况:
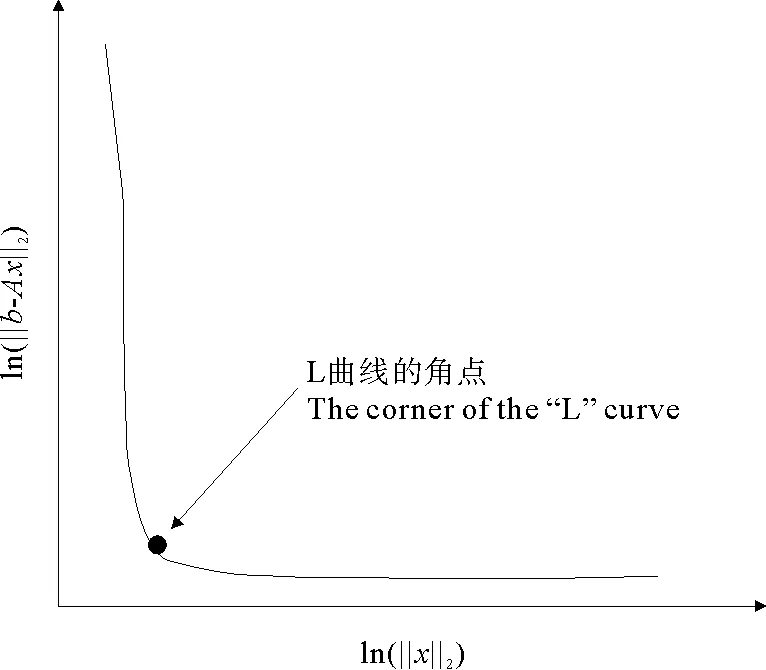
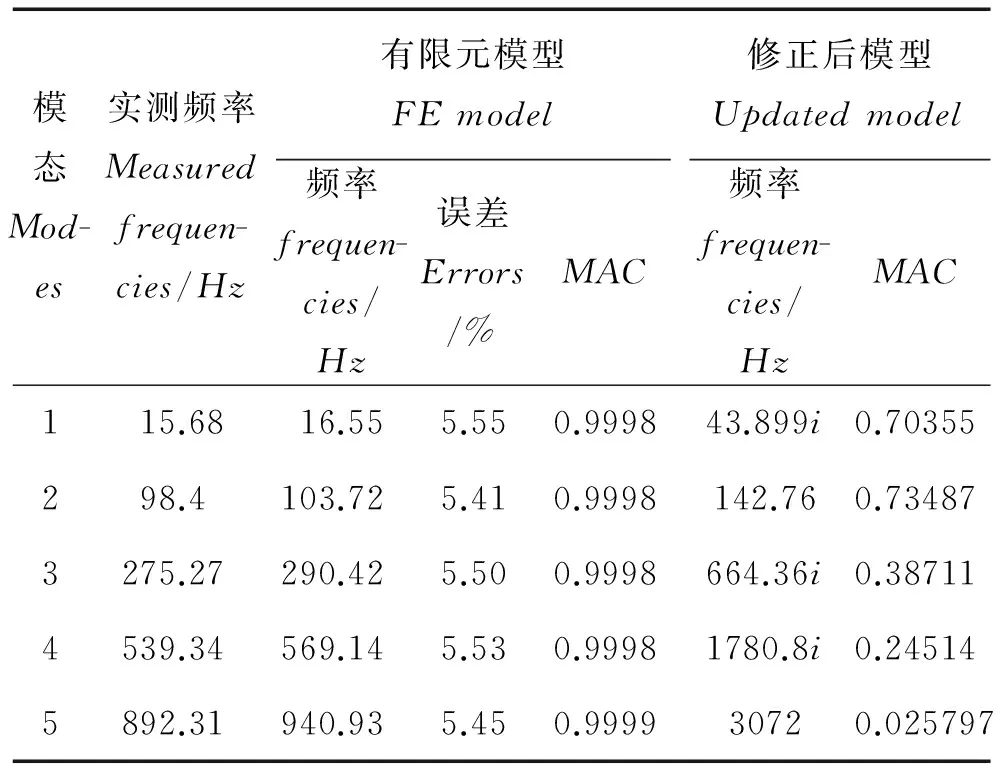
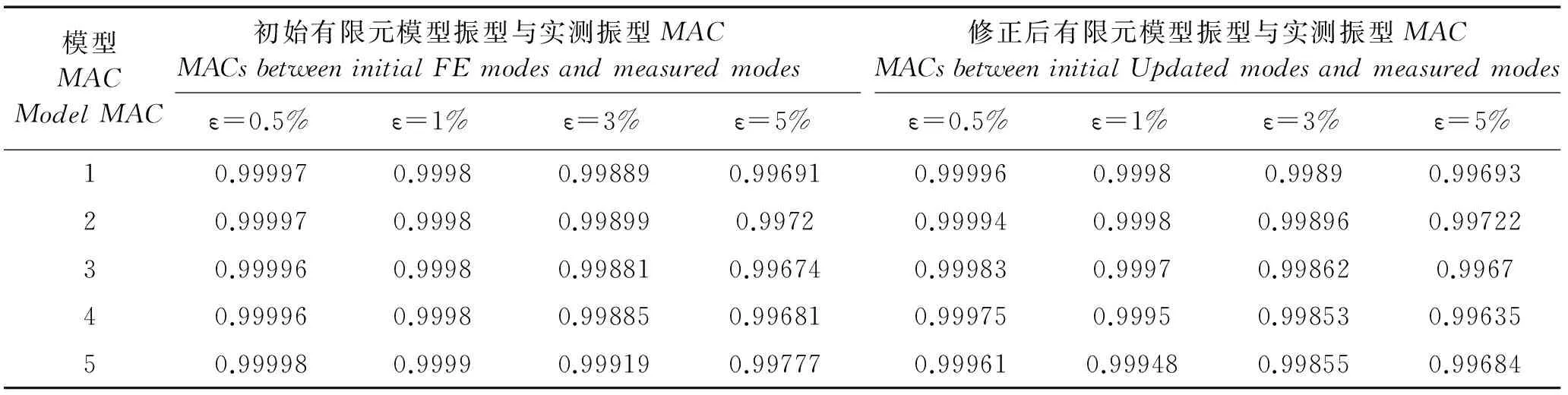
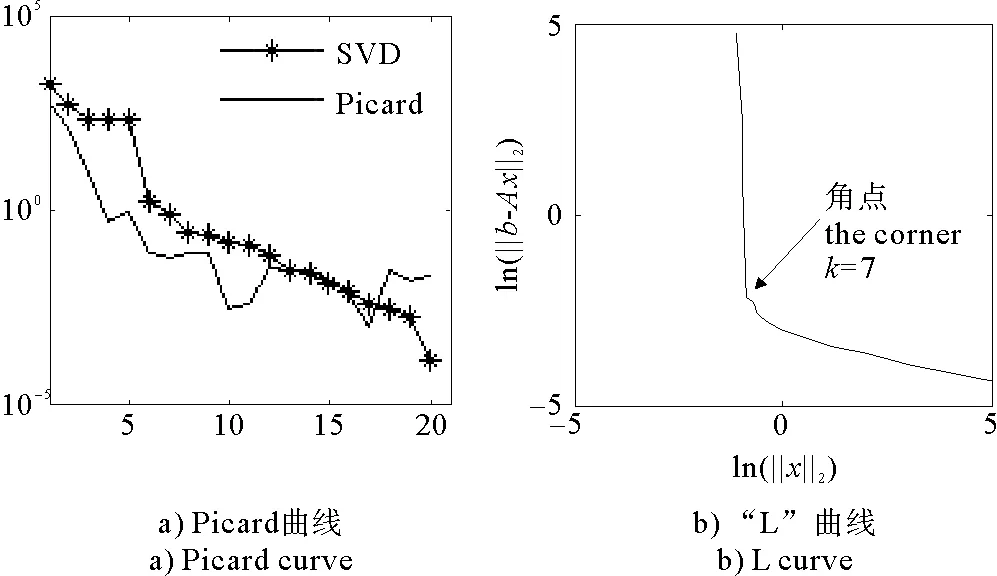
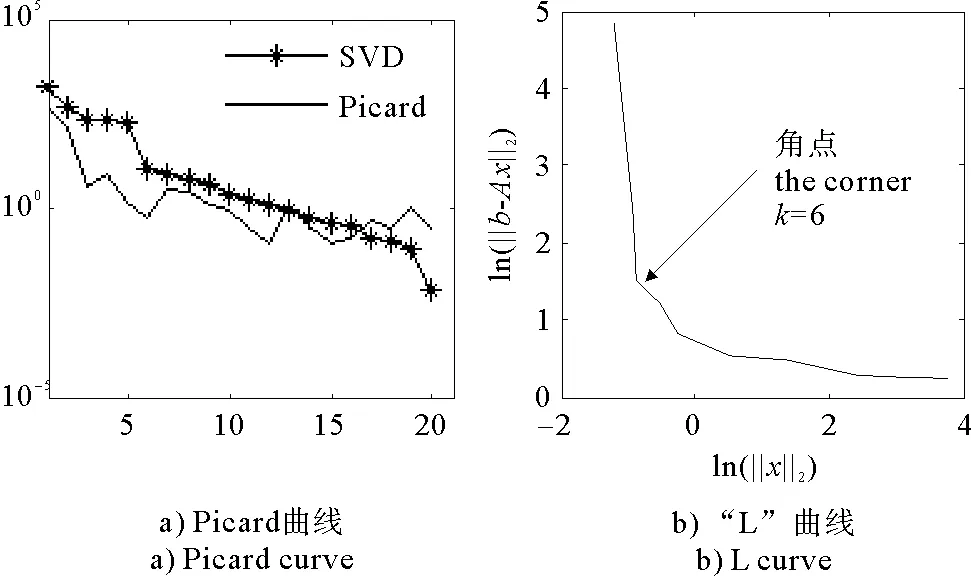
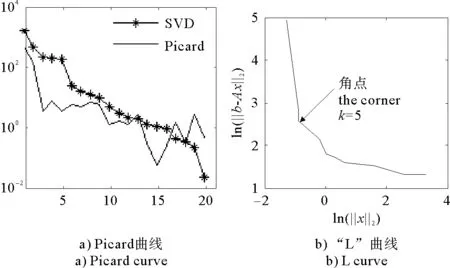
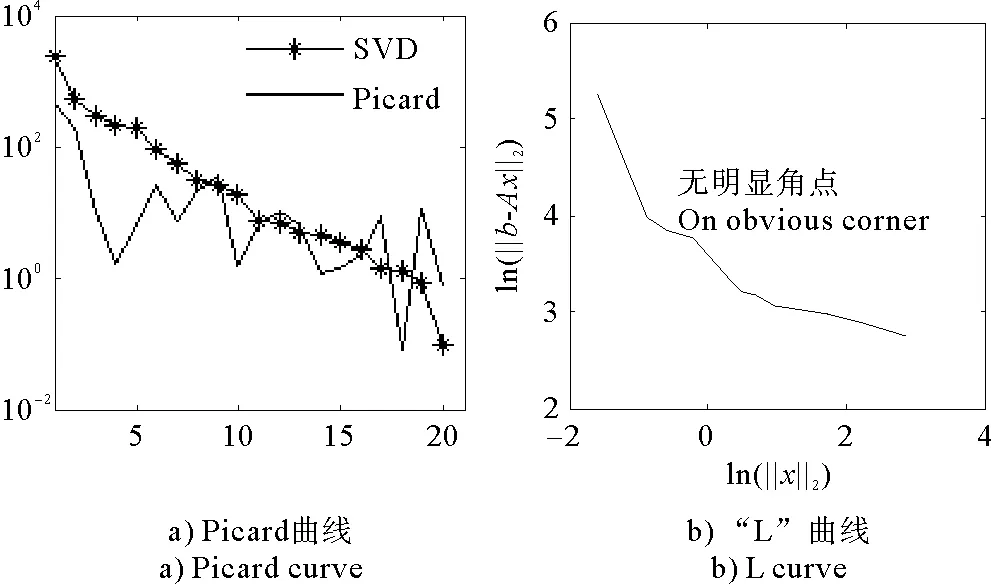
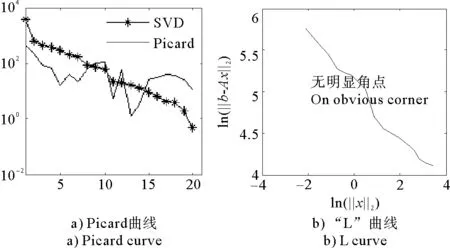
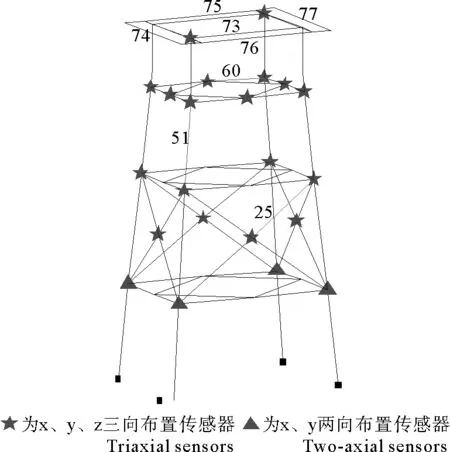
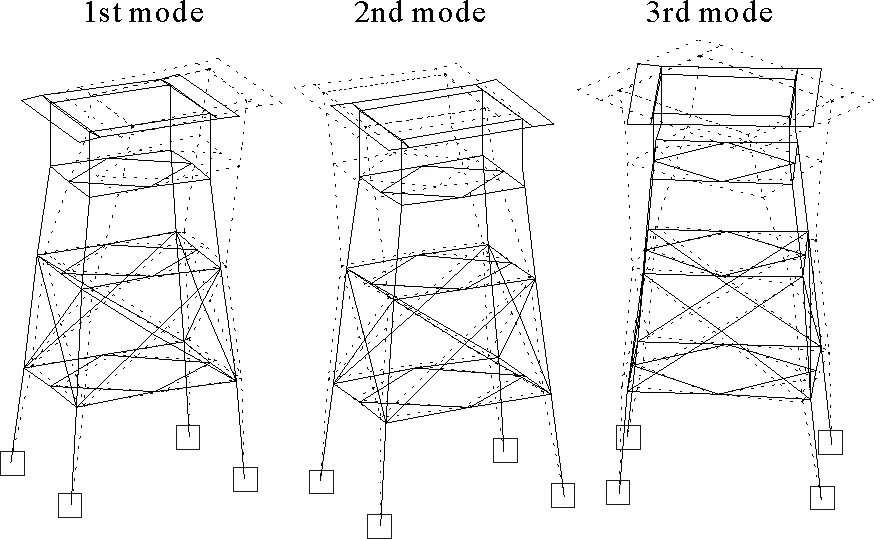
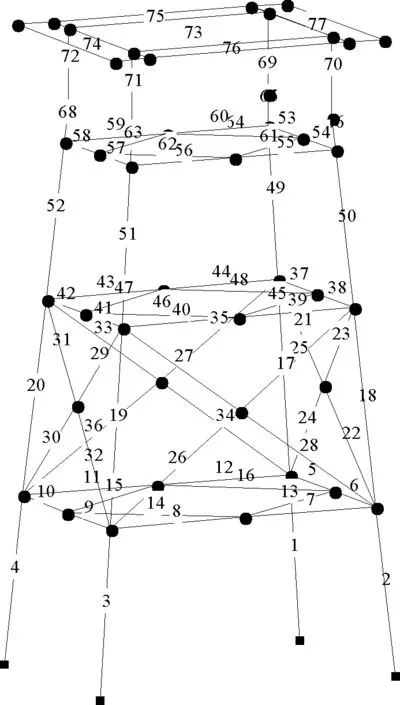
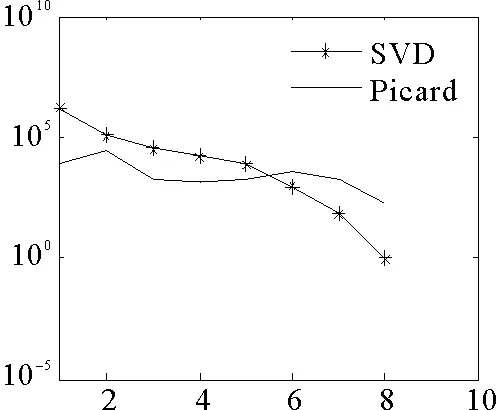
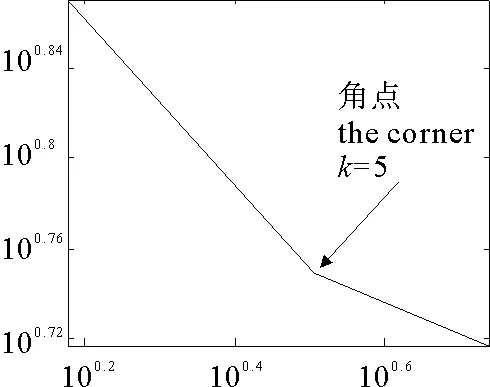
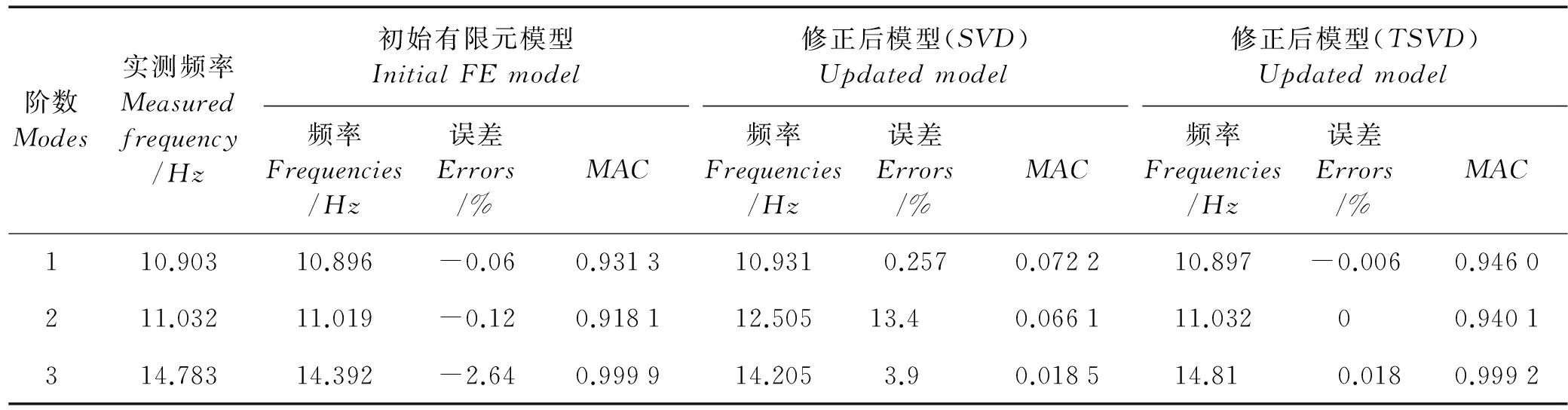
(1)当rank(A) (2)当rank(A)=n,m=n,称为适定系统,可通过标准求逆来进行求解,x=A-1b; (3)当rank(A)=n,m>n,称为超定系统,通常采用最小二乘解来逼近真实解; 而多数实际问题均属于欠定系统、超定系统或者两种系统的组合,称为混合待定系统。对于各类问题,比较通用的求解方法是奇异值分解法(SVD)。 对式(1)的系数矩阵A做奇异值分解: A=UΣVT。 (2) (3) 其中对角阵Σr=diag(σ1,σ2,…,σr)的对角元素为矩阵A的奇异值,且满足σ1≥σ2≥…≥σr>0,r为A的秩。 将酉矩阵U和V分别记为U=(u1,u2,…,um),V=(v1,v2,…,vn),其中u1,u2,…,um和v1,v2,…,vn分别为酉矩阵U和V的列向量,则(2)式可写为 (4) 方程(1)的解可写为: (5) 当有限元自由度较大,修正参数较多且灵敏度差异较大时,模型修正方程组多呈现不同程度的病态,测量数据含有噪声时,会导致该线性方程组的求解发生“振荡”,很难得到有物理意义的修正结果。通常可以通过系数矩阵的条件数来判断其病态性,即最大奇异值与最小奇异值之比。条件数越大,系统的病态性越强,解越不稳定。 测量噪声影响下病态方程组的求解是一个难点问题。Hansen[15]指出,对于式(1)所示线性方程组,如果满足以下3个条件,则可以通过正则解来逼近精确解。 (1)矩阵A的条件数非常大; (2)矩阵A的奇异值逐渐下降趋于零; 通常可以画出系数矩阵A的奇异值曲线(SVD曲线)和离散傅里叶系数曲线(Picard曲线),当SVD曲线在Picard曲线上方时,表示满足该条件;当在下方或重合时即不满足该条件。离散Picard条件的物理意义在于检验线性系统的病态性及受噪声污染的程度。 本节介绍病态线性方程组求解中常用的两种正则化(Regularization)方法:吉洪诺夫(Tikhonov)[9]正则化方法和截断奇异值法(TSVD)[11-12]。 2.1 吉洪诺夫(Tikhonov)正则化方法 对于不适定的修正方程组,最小二乘解的目标是使修正后模型得到最好的拟合,但对某些参数,会出现解的振荡,从而失去物理意义;而最小范数解可以避免出现解的振荡,但其修正拟合效果较差。 (6) 其中Γ为Tikhonov正则化矩阵,通常为微分算子或加权傅里叶算子的离散形式,用以保证解的光滑性。一般取Γ=I或Γ=αI,其中α被称为正则化参数,用于控制最小二乘解和最小范数解之间的平衡。当α值较大时,可以保证‖x‖值较小,但可能会导致解不满足Ax=b;反之,如果α值较小,虽然能得到满足方程组的解,但该解会发生振荡,使得模型修正失去物理意义。α通常取为A的某个奇异值,它的取值对求解非常关键。 假定A的奇异值分解为(4),则方程组(1)的正则解可写为 (7) 其中, (8) 称为Tikhonov因子,它依赖于奇异值σi和正则化参数α。当f(σi)为1时,式(7)即为(5)。由此可见,非零α的作用是过滤掉小奇异值对解的贡献,从而起到稳定解的作用。 2.2 截断奇异值分解(TSVD)正则化方法 截断奇异值法直接舍弃式(5)中的小奇异值。即取过滤因子为: (9) 如果取σ1≥…≥σk≥α≥σk+1≥…≥σr≥0,则正则解为 (10) 其中k称为截断数,当k=rank(A)时,式(10)即为式(5)所示最小二乘解。 截断奇异值法等价于用矩阵 (11) 来近似系数矩阵A。 TSVD正则化方法是Tikhonov正则化方法的一个特例,该过程直接舍弃了小奇异值对解的贡献,一般适用于系数矩阵A的奇异值呈阶梯型分布病态问题[16]。对于杆系结构有限元模型修正问题,其方程组系数矩阵的奇异值多呈阶梯型分布,因此在本文研究中选用TSVD正则化方法进行研究。 2.3 正则化参数的选取 当系统满足离散Picard条件时,对于正则化参数α∈(0,∞)或k∈(1,r),曲线(ln(‖Γx‖2),ln(‖b-Ax‖2))形状呈“L”型,被称为“L”曲线,如图1所示,其角点正好使得最小二乘解和最小范数解得到平衡。因此可通过画出“L”曲线来选择正则化参数。如当采用TSVD正则化方法时,可通过该曲线的最大曲率来确定角点,从而确定截断数k。 图1 “L”曲线图 “L”曲线法选取正则化参数的物理意义明确,应用简单,因此本文选择该方法进行适用性探讨。 本节通过一悬臂梁模型数值算例,将TSVD正则化方法应用到模型修正线性方程组的求解中,通过与基于SVD的最小二乘解修正结果比较,探讨该正则化方法在该类模型修正中的适用性。 3.1 模型介绍 一钢制二维悬臂梁长1m,弹性模量E=2.06×1011N/m2,密度为ρ=7 850kg/m3,截面为30mm×20mm。将梁均匀划分为20个单元,如图2所示,共有21个节点,其中一个节点固定,共有60个自由度。通过特征值分解可以得到其模态频率和振型。 图2 悬臂梁模型 算例中实测模型是通过修改有限元模型各单元的刚度矩阵来进行模拟的。假定实测模型与有限元模型相比各单元间有均值为0.1,标准差为0.01,且呈正态分布的的刚度误差。通过特征值分解,得到修改后模型的模态频率和振型来模拟实测模型的模态参数。 由于在模态测试中,模态频率的识别结果一般较准确,而振型的识别结果常常受测量噪声的影响较严重,因此在本算例中假定实测模态振型含有噪声。为探讨正则化方法的实用性,本算例首先设定噪声水平为1%,添加方式为φi,j=φi,j(1+εRi,j),其中ε为噪声水平;Ri,j为均值为0,方差为1的高斯随机数,φi,j为对应于第i个自由度的第j阶振型值。即在通过数值模拟获得的实测模态振型的基础上添加一定水平的高斯白噪声。 有限元模型与实测模型的前5阶模态对比如表1所示,频率误差均大于5%,振型吻合程度较好。 3.2 基于SVD的最小二乘解修正 利用CMCM方法对20个单元的刚度矩阵进行修正,修正系数取各个单元的弹性模量。取前5阶实测模态和前5阶有限元分析模态,建立模型修正的线性系统Ax=b;其中,size(A)=25×20;cond(A)=2.6536×106;rank(A)=20,与未知数的个数相等,因此理论上有解。 用奇异值分解法(SVD)求取方程组的最小二乘解,并对有限元模型进行修正,结果如表1所示。修正后有限元模型的频率会出现虚数,振型MAC值严重偏离1,因此基于SVD的最小二乘解会导致没有物理意义的修正。 导致以上结果的主要原因是系数矩阵A的条件数较大(cond(A)= 2.6536×106),方程组呈现一定程度的病态,在测量噪声的影响下,最小二乘解发生“振荡”,远远偏离真实值,导致模型修正失去物理意义。 表1 基于SVD的最小二乘解修正结果 3.3基于TSVD的正则解修正 对于3.2中构建的线性系统Ax=b,画出其Picard曲线(其中SVD表示奇异值曲线和Picard表示傅里叶系数曲线),如图3所示。可以看出,矩阵A的奇异值逐渐趋向于零;但从第17个奇异值开始,不能满足离散Picard条件。因此该方程组满足可正则化求解的前两个条件,但只能部分满足第三个条件(离散Picard条件)。 图3 Picard曲线图(ε=1%) 对于以上部分满足离散Picard条件的模型修正线性方程组,本文尝试采用TSVD正则化方法进行求解,并用“L”曲线法选取截断数k。 通过大量试算,画出该系统的“L”曲线,如图4所示。将“L”曲线上位于角点左侧最靠近的点选为截断数,此时k=7。 图4 “L”曲线图(ε=1%) 根据式(10)求出该方程的正则解,并对初始模型进行修正,结果如表3和4所示(ε=1%工况对应结果)。通过比较可以发现,基于正则化求解的模型修正效果很好。由此说明,对于部分满足离散Picard条件的模型修正线性方程组,同样可正则化求解。 为验证“L”曲线法对截断数选取的有效性,分别取k=6, k=8两种情况来进行模型修正,结果如表2所示。通过比较发现,截断数取7时修正效果最好。说明“L”曲线法对于截断数的选取是适用的。 表2 不同截断数的模型修正结果比较 3.4 TSVD正则化方法的噪声鲁棒性探讨 为探讨TSVD正则化求解方法在不同测量噪声水平下的适用性,本部分增加五种噪声工况:0.5%、 3%、5%、10%和20%进行对比研究。修正方程组的构建方式和噪声添加方式同上。 采用奇异值分解法(SVD)进行求解,并对有限元模型进行修正,各噪声工况下结果类似于3.2,修正后有限元模型的频率会出现虚数,振型MAC值会更差,因此最小二乘解会导致没有物理意义的修正。 分别画出各噪声工况下的Picard曲线和“L”曲线,如图5~9,通过比较可以看出,随着噪声水平的提高,方程组对离散Picard条件的满足程度逐渐降低。另外 “L”曲线逐渐趋于平滑,当噪声水平达到10%、20%时,很难通过“L”曲线选定截断数k,如图8~9所示。但对于能够通过“L”曲线选定出截断数的4个噪声工况,均可以通过TSVD方法获得较理想的修正结果,如表3~4所示。 表3 基于TSVD正则解的模型修正结果(模态频率) 表4 基于TSVD正则解的模型修正结果(模态振型) 图5 Picard曲线和“L”曲线(ε=0.5%) 图6 Picard曲线和“L”曲线(ε=3%) 图7 Picard曲线和“L”曲线(ε=5%) 图8 Picard曲线和“L”曲线(ε=10%) 图9 Picard曲线和“L”曲线(ε=20%) 4.1 模型试验 试验模型为某导管架平台的缩尺简化模型,如图6所示。材料为钢材,除导管腿选用Φ20mm×2mm钢管外,其它杆件均为Φ10mm×2mm的钢管。由下而上各层高度分别为:0.41m,0.88m,1.25m和1.53m;工作点高度为1.33m。各层横撑平面尺寸分别为:基底,0.77m×0.54m;一层,0.693m×0.487m;二层,0.6m×0.424m;三层,0.535m×0.375m;工作点以上, 0.52m×0.365m。甲板采用700mm×545mm×10mm的钢板模拟,柱脚采用螺栓固定。 为模拟在役平台的不同损伤工况,立柱、斜撑和横撑均设有局部损伤件(如图10中带有替换件位置,分别对应于有限元模型的25、51和60单元)。 图10 钢质导管架模型及测试仪器 测试采用加速度传感器,信号(经内部放大)直接接入PL16-DCB8 数据采集仪,然后通过网线接入电脑。传感器布置方案如图11所示,共有62个自由度进行了测试。在模型试验中,采用力锤敲击顶层甲板角部,同时激发两个方向的弯曲模态和扭转模态。由特征系统实现算法(ERA)识别到的结构前三阶频率分别为:10.9026Hz,11.0321Hz和14.7827Hz。模态测试其它详细过程可参见文献[6]。 图11 传感器布置示意图 采用文献[10]中介绍的最优拟合法对实测模态进行插值扩阶,振型图如图12所示。 图12 实测振型 4.2 有限元模型 应用Matlab编程,建立该试验模型的有限元模型如图13所示。杆件采用两节点三维梁单元,导管架中每根杆划分为1个单元,共计72个杆单元;甲板采用四节点壳单元,共划分为5个单元。弹性模量取为E=2.06×1011N/m2,密度ρ=7 850kg/m3,采用一致质量矩阵。通过特征值分解,得到有限元模型的模态频率和振型。通过表5中有限元模态与实测模态的对比可以看出,第三阶模态误差相对较大。 图13 导管架平台有限元模型 4.3 有限元模型修正 (1) 修正参数选择 通过试算发现,在总质量一定的条件下,甲板的单元划分及质量矩阵的构建方法,对第3阶频率影响较大。对于本模型,虽然甲板总质量是确定的,但在有限元模型中只划分了五个单元(如图13中73~77单元),且大小不一,势必会造成较大的建模误差。另外由于替换件的设置,局部法兰连接亦会造成实际模型与有限元模型之间的误差。 因此,可以初选甲板73~77单元的质量矩阵,以及25、51和60单元的刚度矩阵作为修正对象,修正参数为相应的质量修正系数β74, β75, β76, β77和刚度修正系数α25, α51, α60,共8个。 (2)模型修正 用前3阶实测模态和前5阶有限元分析模态构建15个CMCM方程,方程组系数矩阵的秩为8,求解8个未知数,理论上有唯一解。 采用SVD方法求取修正方程组的最小二乘解,并对有限元模型进行修正,结果如表5所示,修正后模型的的频率和振型与实测值吻合程度比初始有限元模型更差,修正求解失效。 由该方程组的Picard曲线(如图14所示)可以看出,该系统满足可正则求解的前两个条件,部分满足离散Picard条件,因此可考虑采用TSVD正则化方法进行求解。 图14 Picard曲线 采用L曲线法选取截断数k=5(如图15所示)。根据公式(10)求取该方程组的正则解,并对有限元模型进行修正,结果如表5所示。修正后模型的前三阶频率和振型均有所改善,尤其对于初始误差较大的第三阶模态,修正效果较好。 图15 “L”曲线 阶数Modes实测频率Measuredfrequency/Hz初始有限元模型InitialFEmodel频率Frequencies/Hz误差Errors/%MAC修正后模型(SVD)Updatedmodel频率Frequencies/Hz误差Errors/%MAC修正后模型(TSVD)Updatedmodel频率Frequencies/Hz误差Errors/%MAC110.90310.896-0.060.931310.9310.2570.072210.897-0.0060.9460211.03211.019-0.120.918112.50513.40.066111.03200.9401314.78314.392-2.640.999914.2053.90.018514.810.0180.9992 本文对模型修正病态方程组的求解问题进行了探讨,将数学上常用的TSVD正则化方法和“L”曲线法引入到了模型修正线性方程组的求解中,通过数值和试验研究得出以下结论: (1)当模型修正方程组呈现一定程度的“病态”时,在测量噪声的影响下,最小二乘解容易导致模型修正失效。采用TSVD正则化方法进行求解可有效的解决这一问题; (2)模型修正线性方程组通常只能部分满足离散Picard条件,TSVD正则化方法对此同样适用; (3)TSVD正则化方法求解的关键是截断数的选取,本文研究证明“L”曲线法对于截断数的选取是有效的,但曲线的绘制过程需要进行大量的试算。 (4)当噪声水平较大时,“L”曲线趋于平直,很难通过“L”曲线法对截断数进行选取,因此尚需要探讨其它方法。 [1]FriswellMI,MottersheadJE.FiniteElementModelUpdatinginStructureDynamics[M].Netherlands:KluwerAcademicPublishers, 1995: 2-3. [2]方志, 唐盛华, 张国刚, 等. 基于多状态下静动态测试数据的斜拉桥模型修正[J]. 中国公路学报, 2011, 24(1): 34-41 FangZhi,TangShenghua,ChenSujun,DongYou.Cable-stayedbridgemodelupdatingbasedonstaticanddynamictestdataofmulti-state[J].ChinaJournalofHighwayandTransport, 2011, 24(1): 34-41 [3]RibeiroD,CalcadaR,DelgadoR,etal.Finiteelementmodelupdatingofabowstring-archrailwaybridgebasedonexperimentalmodalparameters[J].EngineeringSructures, 2012, 40: 413-435. [4]ShiradhonkarSR,ManishShrikhande.Seismicdamagedetectioninbuildingframeviafiniteelementmodelupdating[J].ComputersandStructures, 2011, 89: 2425-2438. [5]MojtahediA,LotfollahiYaghinMA,HassanzadehY,etal.DevelopingarobustSHMmethodforoffshorejacketplatformusingmodelupdatingandfuzzylogicsystem[J].AppliedOceanResearch, 2011, 33: 398-411 [6]李英超. 基于模态参数识别的海洋平台结构模型修正技术研究[D]. 青岛: 中国海洋大学, 2012. LiYingchao.Modelupdatingofoffshoreplatformstructuresbasedonmodalparameteridentification[D].Qingdao:OceanUniversityofChina, 2012. [7]WANGS.,LIY,LIH.StructuralModelUpdatingofanOffshorePlatformUsingtheCrossModelCrossModeMethod:AnExperimentStudy[J].OceanEngineering, 2015, 97: 57-64. [8]吴颉尔. 正则化方法及其在模型修正中的应用[D]. 南京: 南京航空航天大学, 2007. WUJie-er.Theregularizationmethodwithapplicationtofiniteelementmodelupdating[D].Nanjing:NanjingUniversityofAeronauticsandAstronautics, 2007. [9]AN.Tikhonov.Solutionofincorrectlyformulatedproblemsandtheregularizationmethod[J].SovietMath,Dokl, 1963, 4: 1035-1038. [10]C.Mares,MI.Friswell,JE.Mpttershwad.Modelupdatingusingrobustestimation[J].MechanicalSystemsandSignalProcessing, 2002, 16(1): 169-183. [11]MI.Friswell,JE.Mottershead,H.Ahmadian,Finite-elementmodelupdatingusingexperimentaltestdata:parametrizationandregu1arization[J].Phil.Trans.R.Soc.Lond. 2001, 359: 169-186. [12]CalvettiD,ReichelL,SgallariFandSpalettaG.Aregularizinglanczositerationmethodforunderdeterminedlinearsystems[J].JournalofComputationalandAppliedMathematics, 2000, 115: 101-120. [13]肖庭延, 于慎根, 王彦飞. 反问题的数值解法[M]. 北京: 科学出版社, 2003. XIAOTingyan,YUShengen,WANGYanfei.Numericalsolutionofinverseproblem[M].Beijing:SciencePress, 2003. [14]HuS-L.J.,LiH.,andWang,S.Cross-modelcross-modemethodfordynamicsystems[J].MechanicalSystemsandSignalProcessing, 2007, 21(4): 1690-1703. [15]HansenPC.Thediscretepicardconditionforill-posedproblems[J].BIT, 1990, 30: 658-672. [16]王振杰. 大地测量中不适定问题的正则化解法研究[D]. 北京: 中国科学院测量与地球物理研究所, 2003. WangZhenjie.Researchontheregularizationsolutionsofill-posedproblemsingeodesy[D].Beijing:InstituteofGeodesyandGeophysicsofChineseAcademyofSciences, 2003. 责任编辑陈呈超 Study on the Application of Regularization Method in Structural Model Updating LIYing-Chao1,WANGShu-Qing2,ZHANGMin (1.CollegeofCivilEngineering,LudongUniversity,Yantai264025,China; 2.CollegeofEngineering,OceanUniversityofChina,Qingdao266100,China) Whilemodelupdatingequationsoflargestructuresalwayspresentsill-conditioning,smallerrorsinthemeasureddatawouldcauseafailuresolution.Inthispaper,thesolutionproblemofill-conditionedandnoisypollutedmodelupdatingequationsisstudied.First,theregularizationmethodscommonlyusedinmathematicsareintroducedtosolvethemodelupdatingequations.Then,numericalexampleofancantileverbeamisstudiedtodiscusstheapplicabilityoftheregularizationmethod.Resultsshowthattheill-conditionedmodelupdatingsystemcanbesolvedeffectivelywithproperregularization.Inaddition,themethodcanalsobeappliedtothemodelupdatingequationswhichpartiallysatisfiesthediscretePicardcondition.Finally,anexperimentstudyofajacketplatformstructureisconductedtoverifythepracticabilityoftheregularizationmethod. modelupdating;ill-condition;regularization;jacketplatform 国家自然科学基金项目(51379196;51209189);山东省自然科学基金项目(ZR2013EEQ006);泰山学者工程专项经费;鲁东大学科研基金项目(LY2013027)资助 2015-03-20; 2015-12-15 李英超(1985-),女,博士,讲师。E-mail:yingchao.ouc@163.com O302;O327 A 1672-5174(2016)09-107-09 10.16441/j.cnki.hdxb.20150032 Supported by the National Natural Science Foundation of China(51379196;51209189); Natural Science Foundation of Shandong Province(ZR2013EEQ006); Taishan Scholars Program of Shandong Province ; Science Foundation of Ludong University(LY2013027)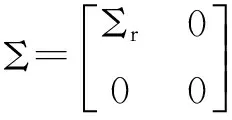
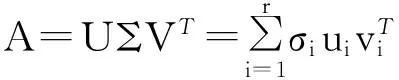
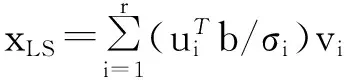
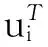
2 正则化方法
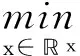
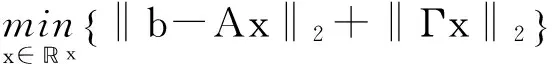
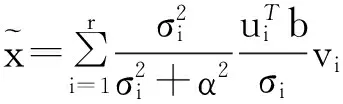
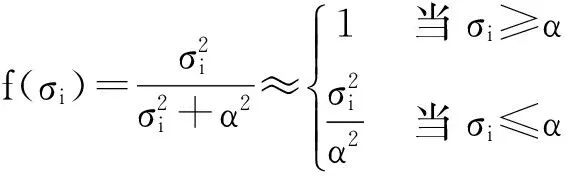
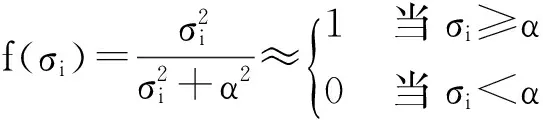
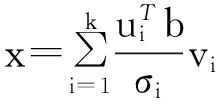

3 悬臂梁模型数值研究

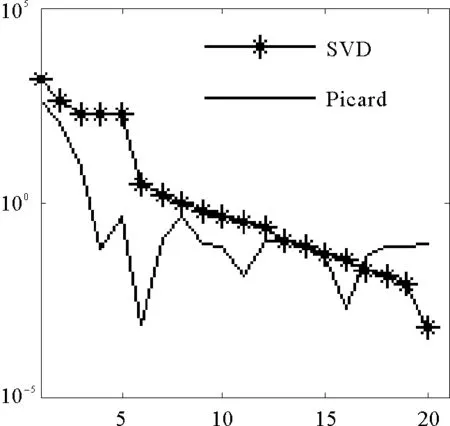
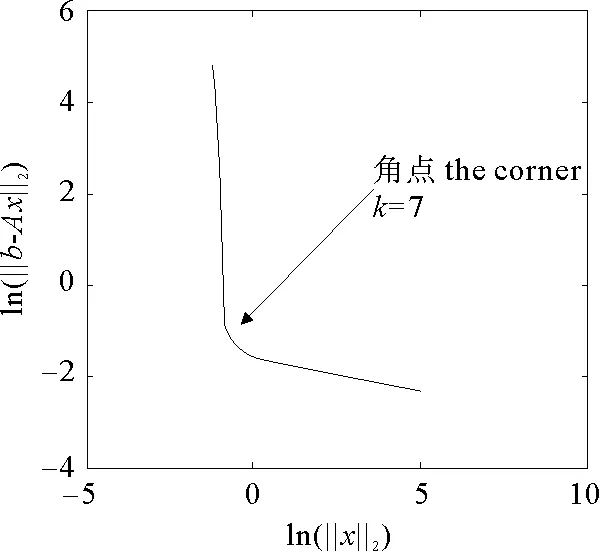
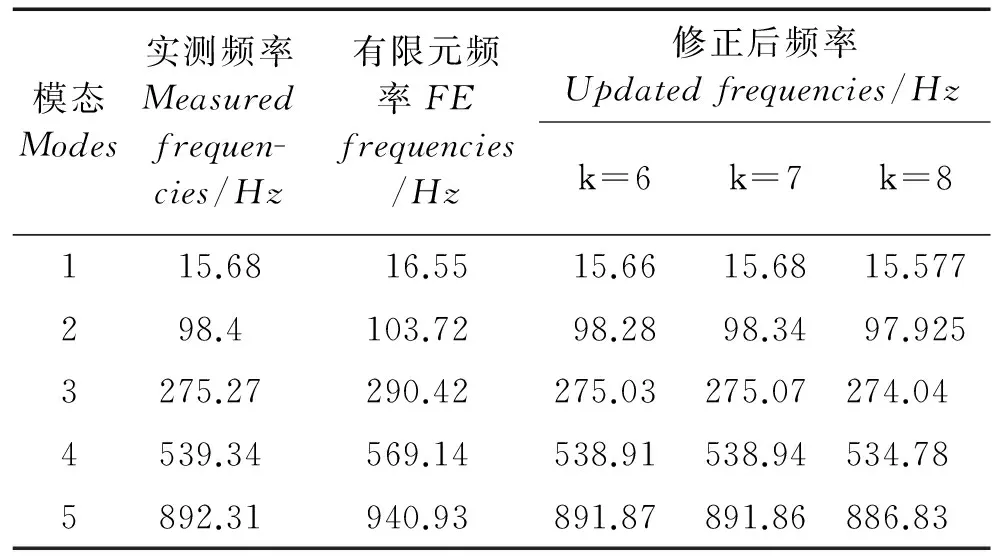
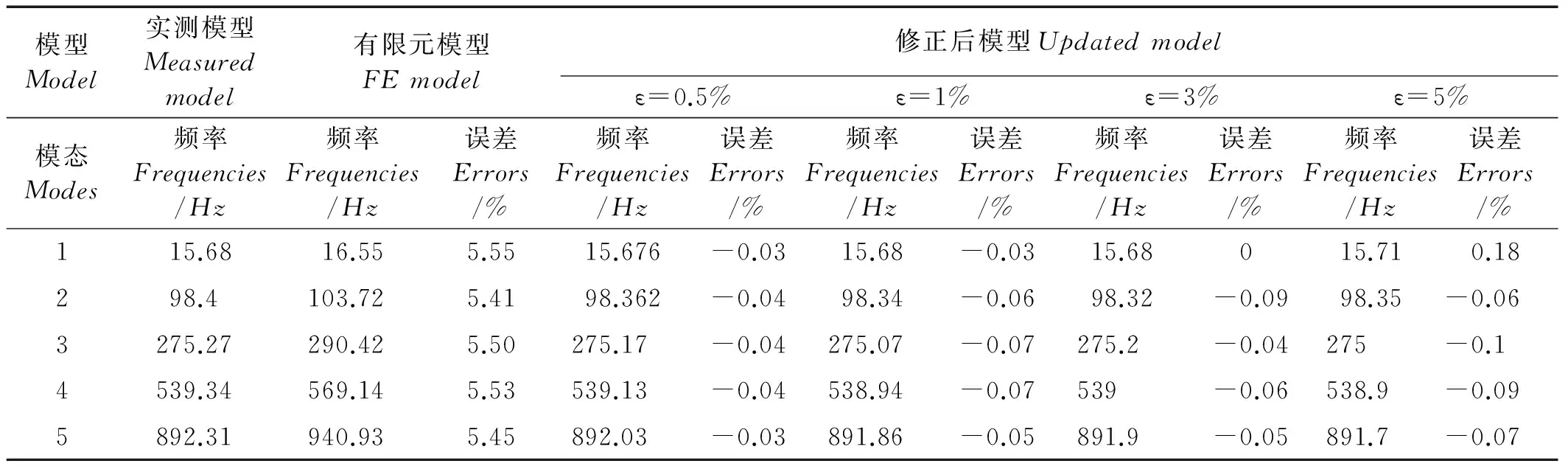
4 导管架平台物理模型试验研究

5 结论

