基于反步法的高超声速飞行器终端滑模控制*

刘艳雯，胡超芳

（1.太原工业学院，太原030008；2.天津大学电气与自动化工程学院，天津300072）

基于反步法的高超声速飞行器终端滑模控制*

刘艳雯1，胡超芳2

（1.太原工业学院，太原030008；2.天津大学电气与自动化工程学院，天津300072）

为了使高超声速飞行器在再入过程中完成姿态控制，在反步法的基础上将模糊自适应和终端滑模控制相结合设计控制器。对于姿态角动态，使用反步法和模糊自适应设计虚拟控制律；而对于角速率动态，利用终端滑模方法设计控制器，能够有效提高系统鲁棒性。稳定性分析说明所提方法可以保证系统状态的一致渐进有界性。

反步法，终端滑模控制，模糊自适应

0　引言

高超声速的概念首先是由钱学森提出的，意指飞行速度能够超过5倍声速。高超声速技术无论在国防还是民用上都有着重要的研究价值，因此，越来越多的科研人员将注意力转移到高超声速飞行器的研制与设计中来。在高超声速飞行器再入阶段，线性控制很难保证全过程的精确跟踪，因此，为了实现姿态控制，近年来提出了一些非线性控制方法，常见的有滑模控制［1］，自适应反步控制［2］，预测控制，以及基于模糊逻辑系统或者神经网络的智能控制方法等［3］。

本文针对带有不确定的高超声速六自由度再入模型，提出了基于反步法的终端滑模控制方法。将被控模型转换成为下三角形式之后，利用反步法对姿态角动态进行虚拟控制律的设计，其中利用模糊自适应对不确定项进行在线跟踪；对于角速率动态，利用终端滑模控制方法解得控制力矩，此方法不仅能够使姿态实现准确跟踪，还能大大增强鲁棒性，有效抵御外部扰动造成的影响。

1　再入模型及其模型转化

1.1高超声速飞行器再入模型

X-33类高超声速飞行器再入模型［4-5］由3个质心运动和3个绕质心的角运动组成。本文控制目标是实现姿态控制，即针对角运动进行控制。其角运动表达式为：

在此姿态角α，β，σ为攻角、侧滑角、侧倾角，而角速率p，q，r为滚转、俯仰、偏航角速率动态。Iij（i= x，y，z，j=x，y，z）表示飞行器的转动惯量。控制输入Mx，My，Mz分别为滚转、俯仰、偏航力矩，控制输出是姿态角动态。质心运动方程、式中相关力表达式以及参数见附录部分。

为了实现姿态控制，即使飞行器跟踪给定的攻角和侧倾角指令，同时使侧滑角保持在零值附近，本文设计了基于反步法的终端滑模控制方法，首先假设如下：

假设1侧滑角始终保持在零附近，因此，假设sinβ=0，tanβ=0，cosβ=1成立。

在以上假设的前提下，将模型进行转换，可以得到下面等价形式：

其中Θ=［α，β，σ］T代表姿态角动态，ω=［p，q，r］T代表角速率动态，M=［Mx，My，Mz］为控制输入，即力矩。式（2）中增益矩阵gs以及矩阵I和Φ的表达式为：

Δf是相关动态构成的不确定项，ΔI是转动惯量Iij（i，j=x，y，z）存在的参数摄动所引起的不确定，Δd是加在控制力矩上的输入扰动，摄动范围和扰动大小在附录部分给出。对上式进行进一步变换，可以得到适用于反步法计算的严反馈形式：

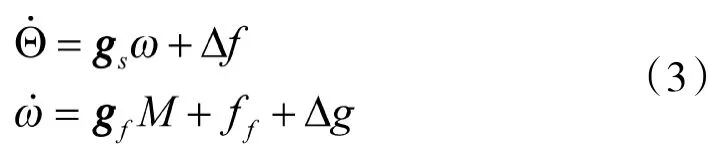
其中gf=I-1，ff=I-1ΦIω，Δg=I-1（Δd-ΦΔIω-ΔIω.）。

2　控制器设计及稳定性分析

本节针对简化模型（3）设计控制器，使其跟踪给定姿态角指令Θd=［αd，βd，σd］T，并且给出稳定性证明。首先假设：

假设2增益矩阵gs存在上下界，即存在常数gsl和gsh，使得gsl≤‖gs‖≤gsh成立。

假设3模糊自适应参数向量θi和逼近误差ε均有界，即‖θi‖≤θi，i=1，2，3，‖ε‖≤εM。

2.1控制器设计

第1步：对于姿态角动态，利用模糊自适应对不确定项进行在线逼近，因此，可表示为：

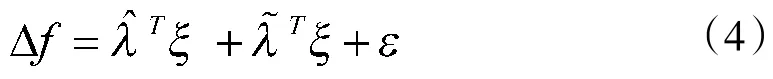
角速率动态ω作为姿态角动态的虚拟控制输入，其虚拟控制指令及自适应更新律为：

式（6）中k1为正定系数矩阵。

第2步：令角速率跟踪误差z2=ω-ωd，z2求导后可得：

为了提高z2的收敛速度和系统的跟踪精度，定义终端滑模面：

其中，γ≥0，p，q为正数，且满足1＜p/q＜2。应用文献［6］所提方法得到实际控制输入M为：

2.2稳定性证明

为了证明系统稳定性，在此选取，

那么对Vs求导后可得：

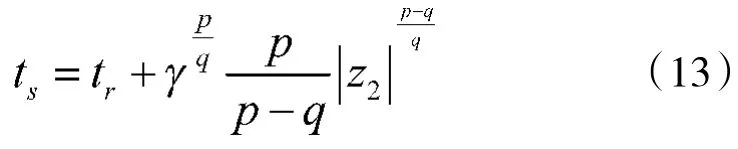
从式（15）可以看出，控制参数选取要满足使得a＞0成立，这样就可以保证跟踪误差z1及估计误差，i，i=1，2，3均有界，稳定性得证。

3　仿真结果

按照所提方法设计控制器，并且对X-33再入飞行器模型进行数值仿真，选取参数为：k1=diag｛25，20，20｝，γ=0.01，p=4，q=3，ρ1=ρ3=2，ρ2=8，σ1=0.3，σ2= 0.5，σ3=0.3，1=3=10，2=50，模糊参数i，i=1，2，3的初始值均设为0，模糊基函数相量，其表达式为［8-9］：

其中，μF（x）是x的隶属度函数，采用高斯形式表达：

其中，x分别为状态α、β、δ，合理选择参数P1，P2，F1，F2使得隶属度函数能够均匀分布。

系统初始条件为：re=21 162 900，φ=0，θ=0，v= 24 061，χ=0，γ=-1.064 deg，α=12.6 deg，β=-11.46 deg，σ=-57.29 deg，p=0，q=0，r=0；姿态角指令Θd=［αd，βd，σd］T=［22.6，0，-17.29］Tdeg，此指令通过一阶滤波器后给到控制器。

模型中的参数摄动范围及输入扰动表达式如下：

仿真效果如图1～图4所示：

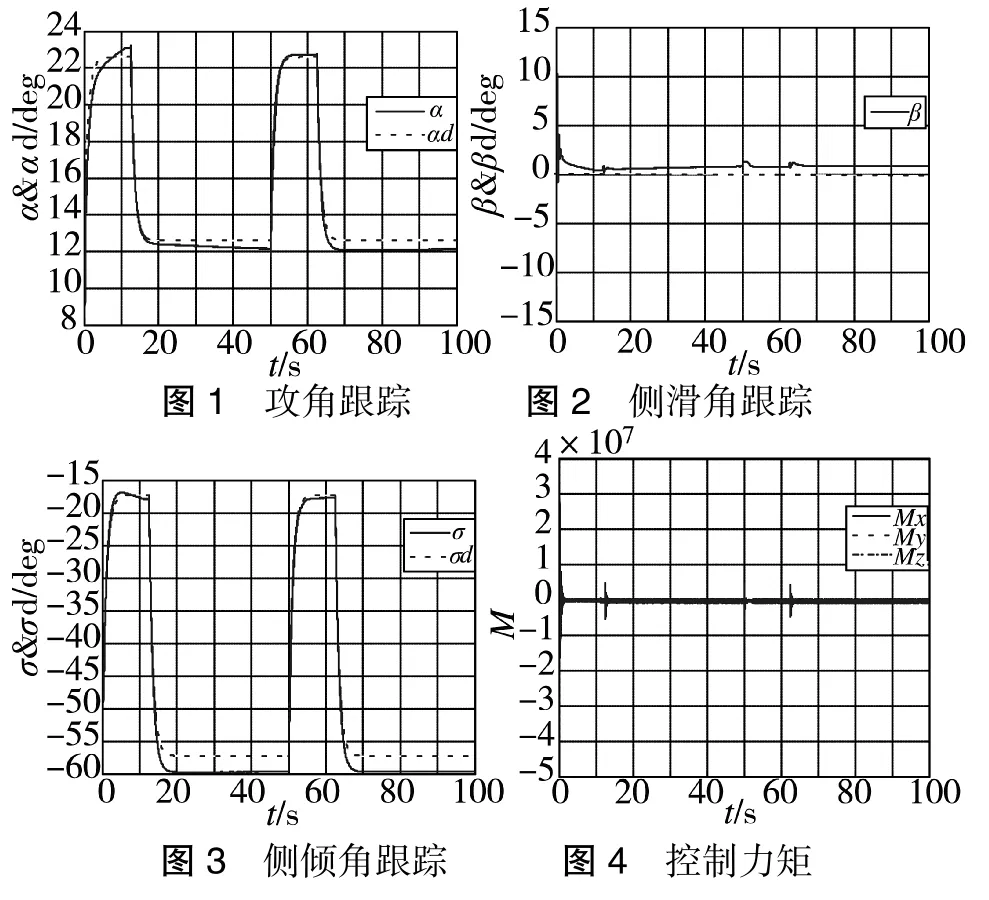
从图中可以看出，所设计控制器跟踪效果良好，且控制力矩变化范围合理。

4　结论

本文针对X-33再入式高超声速飞行器，采用以反步法为主线的终端滑模方法进行控制，并且利用模糊自适应对不确定项进行在线逼近，所提方法能够实现信号的准确跟踪，并能保证系统跟踪误差的有界性。

［1］韩钊，宗群，田柏苓.基于Terminal滑模的高超声速飞行器姿态控制［J］.控制与决策，2013，28（2）：259-268.

［2］LIANBH，BANGH，HURTADO JE，Adaptive backstepping control based autopilot design for reentry vehicle［C］//AIAA Guidance，Navigation，and ControlConfand Exhibit，2004.

［3］SHIZ，ZHANGY F，WANG F.Fuzzy adaptive H2/H∞control formaneuvering reentry vehicle［J］.Control and Decision，2013，28（9）：1365-1371.

［4］DESAIPN，CONWAY B A.Six-degree-of-freedom trajectory optimization using a two-timescale collocation architecture［J］.Guidance，Control，and Dynamics，2008，31（5）：1308-1315.

［5］SHAFFER，PATRICK J.Optimal trajectory reconfiguration and retargeting for the X-33 reusable launch vehicle［PHD Thesis］，Monterey，NavalPostgraduate School，2004.

［6］王坚浩，胡剑波.不确定非线性系统的自适应反推高阶终端滑模控制［J］.控制与决策，2012，27（3）：413-418.

［7］FENG Y，YU X，MAN Z.Non-singular adaptive terminal sliding mode control of rigid manipulators［J］.Automatica，2002，38（12）：2159-2167.

［8］吕海龙.一种基于单向辅助面滑模控制的无人机姿态控制器设计与仿真［J］.四川兵工学报，2015，36（11）：112-117.

［9］胡超芳，刘艳雯.基于动态面的高超声速飞行器模糊自适应非线性控制［J］.控制与决策，2013，12（3）：1849-1854.

［10］BOLLINO K P.High-fidelity real-time trajectory optimization for reusable launch vehicles［C］//Naval Postgraduate School Monterey Cadept of Mechanical and Astronautical Engineering，2006.

（附录略，如需附录部分，请与作者联系）

Term inal Sliding M ode Control for Hypersonic Vehicles Based on Backstepping

LIUYan-wen1，HUChao-fang2
（1.Taiyuan Institute of Technology，Taiyuan 030008，China；2.School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China）

In order to achieve attitude control during reentry process for the hypersonic vehicle，the controller is designed base on backsteppingmethod combining with adaptive fuzzy and terminal sliding mode control.For the attitude angle states，backstepping and adaptive fuzzymethods are used to obtain the virtual control law；for angular rate states，the application of terminal sliding mode control can improve system robustness effectively.The controlled system are ensured to be semi-global uniformly ultimately bounded according to the stability analysis.

backstepping，terminalslidingmode control，adaptive fuzzy

TP273

A

1002-0640（2016）09-0028-04

2015-07-05

2015-09-11

太原工业学院青年科学基金（2015LQ 08）；天津市自然科学基金资助项目（12JCZDJC30300）作者简介：刘艳雯（1987-），女，河北沧州人，硕士。研究方向：飞行器的鲁棒控制。