基于AHP—M L II融合算法的先验分布研究*

赵彬，于雷，周中良，刘宏强，隋永华

（1.空军工程大学航空航天工程学院，西安710038；2.空军工程大学科研部，西安710051）

基于AHP—M L II融合算法的先验分布研究*

赵彬1，于雷2，周中良1，刘宏强1，隋永华1

（1.空军工程大学航空航天工程学院，西安710038；2.空军工程大学科研部，西安710051）

在缺乏可靠性试验数据的情况下，为得到可信的评定结论减少主观影响，需要从信息融合的角度出发，充分利用产品先验信息。以获得关于产品可靠性的更完整和更准确的判断信息，从而进一步形成对产品性能的可靠估计或预测。提出一种基于AHP-ML II的融合算法，对先验信息进行层次分析法处理后，再使用第二类极大似然估计法进行二次处理，通过不同的信息在融合后的先验分布中所起作用的大小，确定出各部分的权重因子，最后通过实例仿真分析得出该算法确实比融合前具有更好的合理性和可靠性。

先验信息，层次分析法，ML-II，融合算法

0　引言

随着科学技术的发展，能够获得可靠性信息的方式途径也越来越多。层次分析法（AHP）是美国T. L.Saaty教授于20世纪中后期提出来的，其特点就是把复杂问题划分为可以相互联系的层次，使之简单化、条理化［1］。文献［2］中胡子义等提出了一种改进的AHP，避免了偏差大、精度不高的问题。文献［3］中基于AHP的思想适用于仿真可信度的评估问题，也进行了AHP法应用于可信度评估的研究。文献［4］中采用ML-II的方法对先验分布进行了权重处理，虽然结果有了很大的改善，但还有很大提高的空间。为了使试验结果更加准确可信，需要尽可能地依赖给定的先验信息来获取先验分布，尽量不使用或者少使用不确定信息［5］。

大多数复杂系统像导弹打靶精度、落入概率等一系列服从正态分布的问题，其特点都是因为受到其在研制过程中成本高、周期长的制约，不可能进行大量的现场试验，无法使试验样本得到充分的评估，而通过具有小子样的特点可以利用先验信息来合理地确定先验分布，这也正是Bayes方法的关键所在［6］。实践证明：分别使用AHP和ML-II方法来处理先验信息都具有很大的局限性，不同的专家经验会导致出现截然不同的结果，基于此本文提出了一种在层析分析法（AHP）融合的基础上，对中间值继续使用第二类极大似然估计（ML-II）方法进行二次融合的方法（即AHP-ML-II融合算法），进一步确定不同先验信息的权重因子，从而给出融合后的先验分布。

1　基于融合算法的先验分布

1.1（AHP-MLII）融合算法的提出

由于受到试验成本和条件的制约，小子样问题普遍存在，而大样本在统计方面又有很大的困难，选择在某项试验进行之前先通过专家信息、历史信息等途径得到不同的先验信息，可以综合运用各种信息，减少现场标准条件下的试验次数，从而有效解决小子样的问题［7］。根据多次试验仿真计算证明，基于AHP-ML-II的融合算法可以很好地提高试验的可靠性，对先验信息在AHP处理后的基础上继续使用ML-II方法进行处理，最终给出融合后的先验分布，使结果更切合实际，更合理有效。

图1　基于层次分析法的第二类极大似然估计方法流程图

下面分别列出AHP和ML-II方法的计算过程，并通过最后的实例分析给出最后的融合结果。

1.2基于层次分析法（AHP）的先验分布融合

在大多数武器装备的研制过程中，对其系列化、标准化的要求越来越高。虽然专家带来的这些经验信息具有很大的主观性，通过本领域内的专家对相应武器装备及其特性和规律方面积累的大量经验，对装备的初步判定能起到很好的帮助，在一定的风险范围内，这些大量的专家信息还是很有价值的。

层次分析法（AHP）是一种将定性与定量结合起来的系统方法，它的实质是一种决策思维方式，把复杂的问题分解开来，并将每一部分赋予权重系数［7-8］。通过建立判断矩阵来进行两两比较，将判断失误率影响降到最低，故其具有很高的可靠性。

1.2.1判断矩阵的建立

对试验中的指标体系，就其重要程度进行两两比较，并将比较结果以数值的形式表示出来，形成判断矩阵。根据图1 B层中各个因素间的相互重要性来得到如表1中的A-B矩阵：

表1　A-B判断矩阵

相对重要程度的取值可以使用表2中的取值方法，即两个因素相比较得出的重要程度。判断矩阵中的主对角线上的元素取值都为1，且aij和aji互为倒数，即得出此矩阵为正互反矩阵［8］。

表2　重要性标度

根据判断矩阵和式（1）来计算权重系数

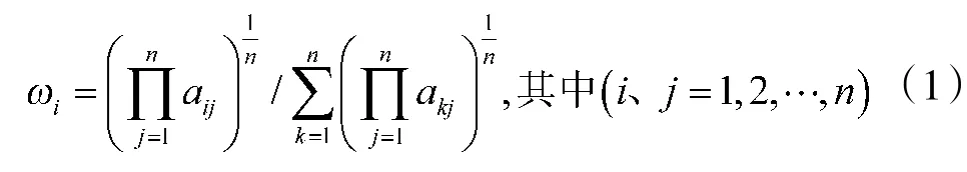
且权重系数之和为1。

其系数矩阵记为：

1.2.2一致性检验

得到权重系数后，接下来需要进行一致性检验。

（2）一致性指标的计算过程，由式（4）：

对应不同的矩阵维数，需要用不同修正因子RI对CI进行修正，通过判断矩阵的阶数n来选择RI的值。

（3）随机一致性比值CR计算：

如果CR≤0.10，可以认为矩阵满足一致性，如果CR＞0.10时说明其一致性没有得到满足，要对其进行修正。可以按照上述方法，对下一级的因素进行分解求的新的权重因子再进行下一次的一致性检验，直至满足为止。假如某专家的评价结果与其他专家相比后的偏差程度比较大，可以将其意见剔除［9］。即CR＞＞0.10说明此信息无效。

1.3基于第二类极大似然估计法（ML-II）的先验分布融合

由于上述所介绍到的层次分析法主观性比较强，导致试验结果具有一定误差性。本文提出一种在AHP方法的基础上使用ML-II方法的融合算法，使试验的先验分布更准确。

设某产品的概率密度函数为f（t|θ），设有m种先验试验数据；有n个试验数据为独立同分布的小子样样本，并且各组试验数据是相互独立的。

令π（iθ）为试验数据获得的先验分布，而融合后的先验分布记作π（θ），则

其中，0≤ωi≤1，ωi为试验先验数据与后验分布的相关权重系数。

对于这种融合方法的目的就是确定其合理的权重系数。这种方法的基本思想是［3］：根据Robbins的经验Bayes理论，采用ML-II方法，将现场试验样本数据看作是由其边缘分布产生的样本，根据在不同的先验分布下，现场样本出现的似然性的大小来确定不同的先验分布在融合先验分布中所起的作用的大小，以此来确定不同先验分布的权重系数，从而确定融合先验分布［9-10］。

假设X=（x1，x2，…，xn）～f（X|θ），而π（θ）为未知参数θ的先验分布，可以由Bayes公式得出θ的后验分布π（θ|X）：

将现场试验数据（x1，x2，…，xn）都认为是边缘分布得到的，则其似然函数的表述为：

根据极大似然估计原理，皆可以求出融合后的先验分布的权重系数ωi。

于是就可以得到：

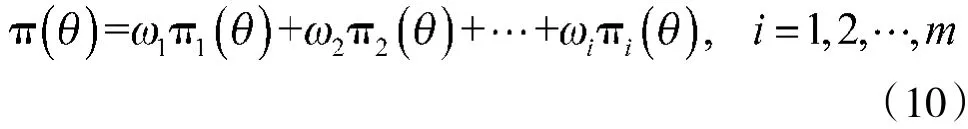
2　实例分析

已知某导弹试验的现场试验数据服从N（θ，1）的正态分布，其中θ为未知参数。在试先验，未知参数θ有3种不同的先验分布。假设通过专家经验列出θ的先验分布π1（θ）=N（9.85，1），由历史试验信息得θ的先验分布π2（θ）=N（10.21，1），由不同环境下的试验信息得出θ的先验分布π3（θ）=N（10.40，1）。先将这3个不同的分布用上文提到的AHP方法进行融合。

（1）首先由表1和表2建立判断矩阵得

由A-B矩阵和式（1）可以计算出权重系数ωi，即W=［0.476 7 0.278 8 0.244 5］T

（2）一致性检验

此方法是由专家信息为背景的融合算法，虽然结果具有一致性，但总体来说主观性比较强，选择不同的专家会有不一样的结果，所以对所得到的权重系数的大小影响比较大，导致最后得到的结果可参考性一般［11］。本文提出的融合算法简单的说就是使用ML II方法对开始AHP所得到的结果进行二次处理。使试验可靠性更高，结论更具说服力。

（3）使用ML-II方法的进一步计算

由仿真程序得到融合后的正态分布中的一组样本数据（9.990，10.252，9.927，10.353，10.322）随机数。通过其边缘分布密度函数

以此通过似然函数来计算权重系数：

则先验分布πAHP1（θ）、πAHP2（θ）、πAHP3（θ）融合之后得到的先验分布：

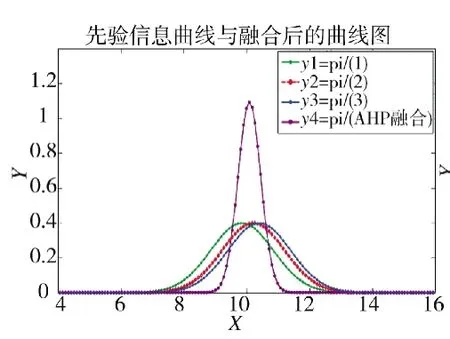
图2　先验信息曲线与融合后的曲线图

图3　AHP曲线与融合后的ML II曲线图

（4）仿真实现由仿真图可以明显地看出：融合后的先验分布被3个融合前的分布都支持的部分函数的值也相应增强了，而其余的部分被减弱了。所以融合后可靠性更强、准确度更高。由图可明显地看到，利用层次分析法融合后的先验信息虽然具有一定的主观性，但也对可靠性起到了很好的加强作用，而且效果明显，得到了W=［0.476 7，0.278 8，0.244 5］T的权重因子，将各类先验信息融合即πAHP1（θ）=N（10.0848， 0.364 8），继续使用ML-II方法处理后得到结果π似然（θ）=N（10.059 8，0.143 6），显然后者的θ值更接近于真实10，其所求得的权重也比较合理。

图4　原始先验信息曲线与分别融合后的曲线对比图

最后由仿真图4反映了使用该方法融合后的先验信息和原始信息以及分别使用AHP、ML-II方法融合信息的对比，由曲线趋势可以明显地看出方法的优越性，使得信息的期望值更接近真实值的同时，方差也有了明显的减小。

3　结论

本文对多源先验信息的融合进行了研究，在尽量减少现场试验次数和试验成本的前提下，最大化地加强信息的可靠性和合理性。着重提出了一种新的融合方法，在对先验信息进行层次分析法处理后再使用第二类极大似然估计方法进行二次处理，经过仿真可看出其可靠性和合理性得到很大的提升且更精确。此方法可以解决此类的一系列难题，通过求权重理清各部分在试验过程的主次关系，对试验结果起到很好的修正作用，在小子样复杂系统可靠性分析中有很大的利用价值。

［1］侯敏，郭基联.多源信息的先验分布融合方法研究［J］.火力与指挥控制，2012，37（7）：57-59.

［2］胡子义，谭水木.层次分析法的一种改进［J］.许昌学院学报（自然科学版），2005，24（5）：26-29.

［3］庞艳静.基于层次分析法的某红外导弹的抗干扰性能评估［J］.红外技术（自然科学版），2014，36（3）：234-237.

［4］廖红强，邱勇，杨侠，等.对应用层次分析法确定权重系数的探讨［J］.机械工程师（自然科学版），2012，10（6）：22-25.

［5］范英，田志成.基于Bayes方法的小子样可靠性分析［J］.机械强度（自然科学版），2012，34（2），274-277.

［6］金振中，李晓斌.战术导弹试验设计［M］.北京：国防工业出版社，2013.

［7］王林，王迎春.层次分析法在指标权重赋值中的应用［J］.教学研究（自然科学版），2002，21（12）：303-306.

［8］ZHANGH Q，YACINEO，VINCENZODS，etal.Selection of product lifecycle management components based on AHP methodologies［C］//Proc.of the International Conference on Advanced Logisticsand Transport，2013：525-527.

［9］冯静，周经伦，孙权.Bayes分析中多源验前信息融合的ML-II方法［J］.数学的实践与认识（自然科学版），2006，36（6）：142-145.

［10］刘琦，冯静，周经伦.基于专家信息的先验分布融合方法［J］.中国空间科学技术，2004，25（3）：68-71.

［11］SONG B W，DONG B C，MAO Z Y，et al.Small sample maintainability testdata fusionmethod based on ML-II［C］//2011 9th International Conference on Reliability，Maintainability and Safety Guiyang，China，2011.

Research on Fusion M ethod for Prior Distribution Based on AHP-M L II

ZHAOBin1，YU Lei2，ZHOU Zhong-liang1，LIUHong-qiang1，SUIYong-hua1
（1.School of Aeronautics and Astronautics Engineering，Air Force Engineering University，Xi’an 710038，China；2.Scientific Research Department，Air Force Engineering University，Xi’an 710051，China）

In some circumstance，the analysis and evaluation should be based on the full use of information provided by all kinds of tests.The prior information must be reliable to execute fewer tests and get a reasonable prior distribution.It can take full advantage of the multi-source reliability information which be acquired at different time or from different place and get a more precise estimation of the product's reliability.For the lack of reliable test information，prior information should be fused and made full use of to decrease the subjective impact.Then a reasonable evaluation or prediction is gained and the information to make judgment is more acute.In this paper，a fusion algorithm of ML-IIbased on AHP is put forward.The prior information is processed by AHP and then by ML-II.The weight of different distributions is gained according to how distributions work after fusion.The resultof simulation indicates that themethod canmake prior information before fusionmore reliable and reasonable.

prior information，AHP，ML-II，fusionmethod

O212.8

A

1002-0640（2016）09-0014-04

2015-06-15

2015-08-08

国家自然科学基金资助项目（61472441）

赵彬（1991-），男，山东济南人，硕士研究生。研究方向：作战试验与评估。