尺度比稳健估计及参考椭球参数确定

李祖锋

(中国电建西北勘测设计研究院有限公司,陕西 西安 710065)



尺度比稳健估计及参考椭球参数确定

李祖锋

(中国电建西北勘测设计研究院有限公司,陕西 西安 710065)

短程精密测距精度一般优于GNSS测量精度，工程中常用GNSS测量与精密测距方法联合建立高精度工程测量控制网，对两者所存在的尺度差异，常采用尺度比进行统一，其关键是尺度比的合理选择。文中参照精密测距边长确定的实测尺度比相对于理论尺度比的残差，建立空间分布与尺度残差线性关系，对尺度差异进行估计并确定合理的尺度比，再在投影层面将尺度比等价转换成参考椭球参数进行数据归算，从而实现GNSS与精密测距成果的高度融合，得到高精度工程测量控制网的可靠成果。

尺度比残差；尺度比差异估计；综合投影变形；椭球参数

短程精密测距精确度一般优于GNSS测量精度，所以工程中常用GNSS测量与精密测距方法联合建立工程测量控制网。由于受到大气折射等因素的影响，以及大部分项目三维平差所引入的位置基准一般采用测站单点定位坐标，精度不高，这些因素在GNSS测量及数据处理环节都会导致尺度发生变化，对于GNSS成果反算边长与精密测距边长所存在的尺度差异，应以精密测距边长作为尺度基准，将GNSS解算边长与精密测距边长的尺度进行统一。

由于高斯投影变形量是一个以至中央子午线距离为自变量的二次幂函数，其投影后的边长变形量沿横向呈二次曲线变化，本文将地面实测边长(为简化计算，地面实测边长不做投影)与GNSS投影至平面的边长比值定义为尺度比，理论上尺度比应符合二次幂函数分布特征，但由于受测量误差的影响，并不符合以上分布特征。测距边在空间上分布一般是不均衡的，生产中采用尺度比算数平均值没有考虑到测距边长在空间分布上的不均衡对其权重的影响，在文献[1]中提出加权尺度比的计算方法，对这个问题进行考虑，文中尺度比计算采用的两组边长精度信息是可以估计的，并可据误差传播定律求出尺度比误差，但文献[1]中尺度比计算没有顾及尺度比自身的精度，仅按照分布特征及其可代表的范围进行确权。本文参照精密测距边长确定的实测尺度比相对于理论尺度比的残差，通过顾及测量边长空间分布及边长误差因素的影响对尺度差异进行估计，从而确定合理的尺度比，然后在投影层面将尺度比等价转换成参考椭球参数进行数据归算，从而实现GNSS解算边长与精密测距成果的高度融合，通过联合平差，得到高精度工程测量控制网的可靠成果。

1　尺度比残差分析

以高斯投影为例进行尺度比残差分析，其高斯投影变形部分可简化

(1)

式中:D1为边长在参考椭球面长度;Ym为所选边端点横坐标平均值;Rm系参考椭球面选定边长中点平均曲率半径。

已知边的参考椭球面边长为D1ab,其投影到高斯投影面上的边长为D2ab，在小范围内，可以近似认为D1ab为平距，则计算理论尺度比Lt为

(2)

设己知GNSS控制网a，b两点的反算边长为DGab, 精密测距平距为Dab,实测边长与GNSS成果反算边长计算尺度比为

(3)

由式(2)、式(3)确定尺度比残差，则

(4)

式中:Lir做为测量值;Lit被认为真值。

如果测量数据不存在系统性偏差，则E(ΔL)=0，即ELr=Lt。

2　尺度比差异值的确定

2.1尺度比差异最小二乘线性回归分析

考虑到参与尺度比计算的边长沿空间分布是不均衡的，尺度差异仅采用算数平均计算，并没有考虑到测距边长在空间分布不均衡对其权重的影响，为了估算出测区尺度比残差值，应按照各个区域的尺度比所代表的范围进行定权，用横坐标Yi来表达测距边长的空间分布，借助线性回归方程进行尺度差异的分析，以测区中央部位回归直线的数值作为最终的尺度差异结果。

由此确定残差ΔLi与Yi的线性关系为

(5)

式中：Yi为选定边长距离中央子午线距离；Δ，ε为系数；ei为随机误差。

通过线性相关系数ρ判断尺度残差数据中是否存有异常数据，即

(6)

令

(7)

由最小二乘求解算式[2-4]，得

(8)

求解法方程组得

(9)

系数Δ为尺度差异的常数量，当ε近似于0时，各个时段的尺度是一致的，但普遍情况下，多时段观测受外界因素的影响而存在系统性的尺度差异，ε数值的大小可部分反映这种差异的量级，但不完全。

残差值

(10)

中误差

(11)

中误差可反映出项目随机误差的规模。

对于存在大误差的数据，应采用稳健的估计方法进行参数解算。

2.2尺度比残差稳健估算方法

设GNSS测量边长误差为σG，实测边长误差为σ，据误差传播率得尺度比误差算式知

(12)

由式(12)可看出，所求尺度比精度与边长及边长测量精度相关，较大的误差以及较短的边长均会导致参数解算误差增大，对于这部分数据有必要采用更稳健的方法进行估算。下边建议两个稳健的估计方法，对于测距边数量较多的项目采用最小二乘稳健估计方法，对于测距边较少的项目采用最小一乘估算方法，最小一乘和二乘的使用界定，以试算结果作为参考，一般建议边长少于5条，采用最小一乘方法。

最小二乘稳健估计方法将残差作为统计量，在所选定的显著水平下，判断其是否满足所设定的期望，对异常数据降权或者剔除处理。抗差最小二乘方法如下：

Ρ函数为ρ(u)=|u|，相应的权因子为

(13)

(14)

现在讨论计算中实测边长较少的情况，边长较少时，最小二乘方法会放大尺度比异常偏差影响[3]，虽然稳健估计对异常尺度差异进行了降权或者剔除，但有时这种异常数据恰好反映某些区域的尺度信息，不应该随意降权或者剔除。最小一乘方法可以克服最小二乘的上述缺点。其要求实测点到回归直线的纵向距离的绝对值之和为最小，针对小样本，“稳健性”好于最小二乘法。求出Δ，ε,使得不同位置的尺度差异沿y轴到直线ΔLi=Δ+εYi的偏差绝对值和最小 ,即

(15)

最小一乘线性回归参数估计算法：

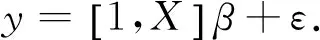
(16)

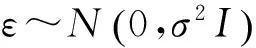
最小一乘线性回归系数β的估计，需要了解无约束不可微最优化问题，即

(17)

即要求超定矛盾线性方程组

(18)

的l1范数极小解。

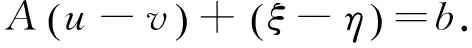
(19)

(20)

最小一乘系数计算采用 MATLAB实现 。

3　基于尺度比残差确定参考椭球参数

当测区尺度比一致时，确定的系数ε应该是一个很小的数值，可以忽略，所求出的Δ一般就是所求的总体尺度差异ΔL=Δ，则修正后的尺度比为

(21)

若ε较大，存在沿测区分布不一致的系统误差，应查找数据问题，如果认为这个数值可接受，则计算测区中央回归线偏离值，并修正到ΔL上，即

(22)

式中：YM为测区中央横坐标，YM=(Ymin+Ymax)/2。

为了便于尺度参数在数据转换中的实现，将尺度差异代入抵偿投影算式，Hm为基于尺度比残差所确定的抵偿投影面高程值。

(23)

椭球不同位置半径可通过椭球参数确定。标准参考椭球面子午圈为长半径为a,短半径为b的椭圆,设椭圆的参数方程为

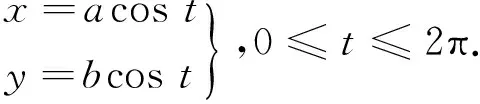
(24)

则椭圆上任意点处的半径为

(25)

(26)

将b=(1-α)a代入式(26)得

(27)

则工程区域选定投影面的平均地球曲率半径rE为

(28)

保持原有的参考椭球扁率等不变，通过膨胀参考椭球长轴a对高斯投影变形进行抵偿，设工程参考椭球的长半轴为rE，可以建立关系式

(29)

4　结束语

为解决精密测距边长与GNSS测量尺度不一致的问题，参照精密测距边长确定实测尺度比相对理论尺度比的残差关系，分析尺度比残差特征，借助线性回归方程，建立空间分布(距离中央子午线距离)与尺度差异线性回归关系，抑制测距边长在空间上分布不均衡对尺度比计算结果的影响。对于边长过短或者误差过大的测距边，采用稳健的估计方法进行参数估算，减小测量误差对参数估算的干扰，可较好解决测区总体GNSS与精密测距边长尺度差异问题[8-10]。为便于尺度差异参数在数据转换中的实现，在抵偿投影层面，将尺度比等价转换成抵偿投影高程面，并通过确定测区地球曲率半径，将抵偿投影高程值转换成参考椭球参数进行数据归算，实现GNSS测量成果与精密测距边长的高度融合。

[1]李祖锋，赵彦华，巨天灵.限制GPS边长综合投影变形加权尺度比算法[J].工程勘察，2010(7):76-79.

[2]宋爱斌.数理统计理论、应用与软件实现[M]北京:国防工业出版社,2010．

[3]王福昌.最小一乘回归系数估计及其 MATLAB 实现[J].防灾科技学院学报, 2007(12):85-89.

[4]邱卫宁.测量数据处理理论与方法[M].武汉:武汉大学出版社．

[5]李祖锋.基于尺度比确定工程参考椭球长半径[C]//《测绘通报》编辑部.第二届“测绘科学前沿技术论坛”论文精选.北京：2010(2):136-137.

[6]李祖锋.限制边长投影变形最佳抵偿投影面的确定[J].工程勘察，2010(2)：75-78.

[7]陈丽华,汪孔政.关于参考椭球平均半径的探讨[J].测绘通报,2000(10):15-17.

[8]施一民, 张文卿.区域椭球元素的最佳确定[ J].测绘工程, 2000，9(3):27-29

[9]李祖锋，巨天力，张成增，等.基于重力场模型高程拟合残差求定GPS正常高[J].测绘工程，2010，19(4)：24-27.

[10] 李祖锋，高建军，缪志选，等.利用最优抵偿投影面算法限制GPS边长投影变形[J].测绘工程，2010，19(2)：75-77.

[责任编辑：张德福]

Robust estimation on scaling-ratio and determination of reference ellipsoid parameters

LI Zufeng

(Powerchina Xibei Engineering Corporation Limited, Xi’an 710065, China)

The precision under precision measurement with short distance is higher than that under GNSS. So generally, combining GNSS with precision measurement, this paper proposes a high precision engineering surveying control network for project. For the scale difference between the two, scale ratio is used to unify, and the key is the reasonable choice of scale ratio. Based on the residual of actual scale ratio to theory scale ratio referring to the precision measurement length, the paper establishes the linear relationship between the spatial distribution and the scale residuals, and estimates the scale difference and determined the reasonable scale ratio.Then at the projection level, the scale ratio is equivalently conversed into reference ellipsoid parameters for data imputation, so as to realize the high integration of GNSS and precision measuring results, and to receive reliable results of high precision engineering survey control network.

scaling-ratio residual; difference estimation; integrated projection deformation; ellipsoid parameter

10.19349/j.cnki.issn1006-7949.2016.12.001

2015-05-28

中国水电工程顾问集团科技项目 (GW-KJ-2012-21)

李祖锋(1981-)，男，高级工程师.

P221

A

1006-7949(2016)12-0001-04