转子-轴承系统中滚动球轴承的非线性动力学相似特性研究†

罗忠　郭健　唐瑞　韩清凯　王德友

(1.东北大学机械工程与自动化学院, 沈阳　110819) (2.大连理工大学机械工程学院, 大连　116023) (3.中航工业集团沈阳发动机设计研究所, 沈阳　110042)



转子-轴承系统中滚动球轴承的非线性动力学相似特性研究†

罗忠1*郭健1唐瑞1韩清凯2王德友3

(1.东北大学机械工程与自动化学院, 沈阳110819) (2.大连理工大学机械工程学院, 大连116023) (3.中航工业集团沈阳发动机设计研究所, 沈阳110042)

针对转子-轴承系统中滚动球轴承的动力学相似问题,提出一种考虑非线性振动特性的轴承系统相似模型建立方法.首先,建立滚动球轴承整体的非线性振动微分方程,运用积分模拟法推导了轴承整体的非线性振动特性相似关系,并结合滚动球轴承的动力学相似关系得到滚动球轴承系统的相似设计准则；其次,应用所得的相似准则,以深沟球轴承C204JUT为原型、6208为模型进行数值仿真实例计算,通过采用Newmark-β算法计算得到的分叉图分析了转速ω、径向载荷Fr、阻尼C及径向游隙γ大小对原型和模型轴承系统振动位移或速度响应的影响；最后,通过对比原型和模型的各参数(ω、Fr、C、γ)分叉图中分叉区间、趋于稳定运动参数值大小以及进入稳定周期运动时的稳态响应值大小验证相似准则的准确性和有效性.通过分析得到以下结论：①滚动球轴承非线性振动特性参数(如振动响应、结构阻尼等)相似关系可由轴承结构参数相似关系确定；②原型与模型非线性运动的分叉图形状一致,且模型能够很好的预测原型稳态振动响应,因此可将模型轴承用来预测原型轴承的非线性振动行为.

转子-轴承系统,滚动球轴承,非线性特性,动力学相似

引言

轴承作为转子-轴承系统中重要支承部件,其动力学特性对系统振动特性影响较大[1-2].在进行转子-轴承系统相似研究时,轴承部分往往只以特定刚度矩阵参入研究,但轴承为组合件,其结构与运动的复杂性决定此种形式必然导致所建立的相似模型不精确,相似模型不能准确预测出原型动力学特性,因此,对滚动球轴承系统动力学特性相似的研究尤为重要.

关于轴承动力学相似研究的开展时间较早,但文献并不多见.早在1969年,Constantinescu得出动压滑动轴承定常气体润滑膜的相似准则,并指出其相似准则与哈里森数(Harrison’snumber)相等[3].后来,2007年,文献[4]基于相似理论分析了滚动轴承保持架模型的动力相似判据,得到模型保持架和实物保持架各动力参数的相似关系,并进行了保持架模型动态特性试验.2008年,文献[5]用量纲分析法推导得变桨距回转轴承的静力模型和动力模型的相似准则,并用有限元方法验证了相似准则的正确性.2009年,文献[6]针对舰船尾部滚动轴承运用相似理论推导出相应相似准则,并建立了试验台架模拟实船尾部轴承受力和润滑的关系.2013年,文献[7]推导了滚动球轴承动力学相似关系,并依据赫兹理论计算原型及模型接触刚度,验证所推相似关系准确性.以上研究工作都忽略了非线性因素,但在实际工程中很多动力学现象用线性理论解释不清楚,必须考虑非线性因素[8-10],这也是非线性动力学被受到广大学者越来越重视的重要原因.

前期学者的研究只针对单个轴承或其某个部件(如保持架)的相似问题进行研究,对轴承系统相似问题的研究从未涉及.本文基于滚动球轴承系统非线性振动微分方程,结合滚动球轴承动力学相似关系,推导出滚动球轴承系统相似关系,并采用算例验证所得相似关系的准确性.

1　滚动球轴承非线性振动方程建立

滚动球轴承由滚动体、保持架及内、外环组成,其中滚动体与内、外环之间有相对运动,其对轴承振动特性有重要影响,转子-轴承系统中滚动球轴承结构如图1所示.

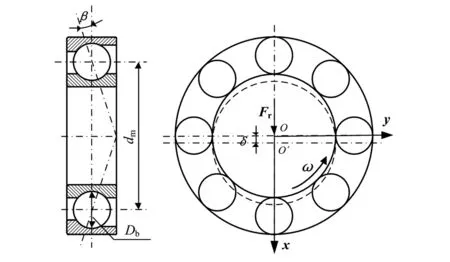
图1　滚动球轴承系统结构示意图Fig. 1　General view of the rolling-bearing system

图1中,di为轴承内环直径；do为轴承外环直径；dm为轴承中径；Db为滚动体直径；β为轴承滚动体的工作接触角；z为滚动体数.设ω为轴承内环的转动速度；Fr为径向载荷；δ为轴承接触总变形,图中虚线表示受载后内圈位置.则轴承中第j个滚动体在时间t时的位置角度θj为[11]：

(1)

式中,ωc为滚动体公转角速度,ωc=ω·di/(di+do).

由赫兹接触理论知,滚动球轴承在工作过程中由于滚动体与内、外环的接触变形会产生非线性轴承力,将其分解到x、y方向可表示为[12]：

(2)

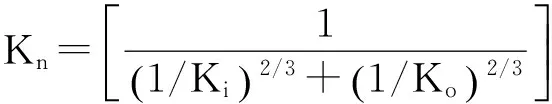
由于一般认为滚动轴承的交叉刚度很小可以忽略不计,因此可由式(2)得到轴承系统的刚度为[13]：

(3)

轴承在运转过程中不仅受恒定的径向外载荷力作用,而且还不可避免的受到由轴承中存在的不平衡量引起的周期性不平衡力的作用[14].故根据Lagrange方程可建立转子-轴承系统中的滚动球轴承的非线性振动方程[15]：

(4)

式中,M为轴承系统的质量；C为轴承系统的阻尼；em为轴承系统的不平衡量偏心距.

滚动轴承运转过程中会发生变刚度振动(Varyingcompliancevibration),即当内环转动时,滚动体每通过载荷的作用线一次,就产生一次周期性的振动.变刚度振动是由轴承径向载荷引起的非线性振动特性,其振动频率fvc与滚动体的数目和滚动体的公转角速度有关,可表示为[16]：

(5)

2　滚动球轴承非线性相似关系建立

2.1滚动球轴承动力学相似关系

作者在文献[6]中已由量纲分析法推导了滚动球轴承动力学相似关系,其相似关系为：

(6)

式中,λi为参数i的相似比,是模型与原型的比值；k为轴承接触刚度.

2.2滚动球轴承非线性振动相似关系

由轴承非线性振动方程式(4)可知：滚动球轴承系统振动的激振力主要由径向外载荷和不平衡力两个部分组成.

将积分模拟法运用到式(4)中,可得滚动球轴承系统相似准则为：

(7)

结合滚动球轴承动力学相似关系式(6),由式(7)可得出滚动球轴承非线性振动相似关系：

(8)

由于轴承非线性力的振动频率与外激励频率存在式(5)的关系,故可得出滚动球轴承外激励频率相似比为：

(9)

3　实例验证

以深沟球轴承C204JUT及6208分别作为计算原型及模型,对比其非线性特性,如不同转速、径向载荷、阻尼及径向游隙下的位移、速度及加速度响应值等[17],验证所推得滚动轴承非线性振动相似关系准确性,其基本参数如表1所示.

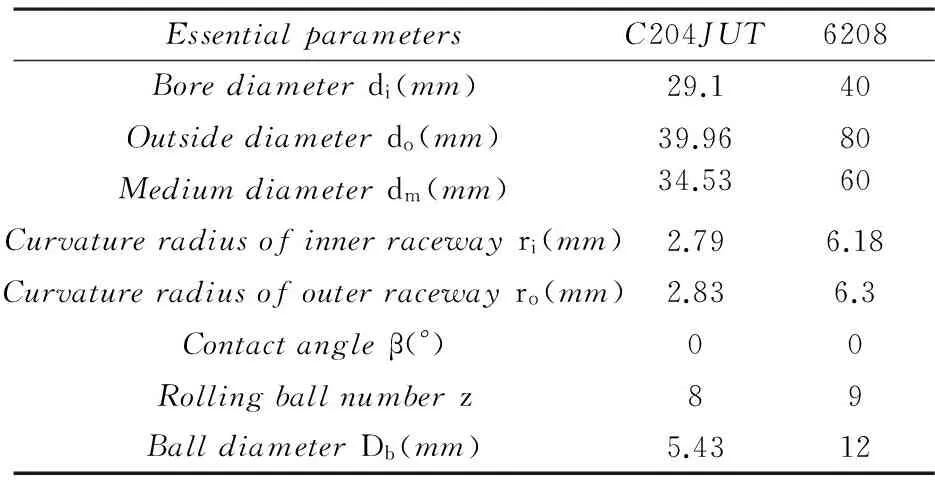
表1　深沟球轴承C204JUT及6208参数

由式(8)、(9)可计算出原型与模型相似比：

λFr=λM=7.6540;λx=λy=λem=λγ=2.7565;

λω=0.6023;λωvc=0.6768;λC=4.6101

3.1响应随转速变化

设原型计算初始参数：Frp=5N；γp=20μm；emp=0m；Mp=1kg；Cp=300N·s/m.则模型计算初始参数：Frm=λFrFrp=37.27N;γm=λγγp=55.13μm;Mm=λMMp=7.6540kg;Cm=λCCp=1383.03N·s/m.

采用Newmark-β法求解原型及模型振动方程,可得出原型及模型随转速变化位移分叉图,如图2所示.

图2　随转速变化位移分叉图Fig. 2　Bifurcation diagrams: displacement-rotating speed relationships

对比图2可以看出,原型及模型均经历非周期-1周期-非周期-1周期-非周期,最后由2周期变为1周期振动,直至稳定过程,且原型进入稳定周期时转速为19600r/min,模型进入稳定周期时的转速为12530r/min,原型及模型非线性现象相同.

分别做出原型在转速19600r/min、模型在转速12530r/min时的稳态位移响应图,如图3所示.

图3　稳态位移响应值Fig. 3　The time history curves of the steady displacement

3.2响应随径向力变化

设原型计算初始参数：ω=10000r/min；γp=20μm；emp=0m；Mp=1kg；Cp=300N·s/m.则模型计算初始参数：ωm=λωωp=6768r/min;γm=λγγp=55.13μm;Mm=λMMp=7.6540kg;Cm=λCCp=1383.03N·s/m.

采用Newmark-β法求解原型及模型振动方程,可得出原型及模型随径向力变化速度分叉图,如图4所示.

对比图4可以看出,原型及模型均经历非周期-1周期-非周期-1周期振动,直至稳定过程,且原型进入稳定周期时径向力为22.3N,模型进入稳定周期时径向力为139.3N,原型及模型非线性现象相同.

分别做出原型在径向力23N、模型在径向力140N时的稳态位移响应图,如图5所示.

图4　随径向力变化速度分叉图Fig. 4　Bifurcation diagrams: velocity-radial loading relationships

图5　稳态速度响应值Fig. 5　The time history curves of the steady velocity

3.3响应随阻尼变化

设原型计算初始参数：ω=10000r/min；γp=20μm；emp=0m；Mp=1kg；Fr=5N.则模型计算初始参数：ωm=λωωp=6768r/min;γm=λγγp=55.13μm;Mm=λMMp=7.6540kg;Frm=λFrFrp=37.27N.

采用newmark-β法求解原型及模型振动方程,可得出原型及模型随阻尼变化位移分叉图,如图6所示.

对比图6可以看出,原型及模型均经历非周期-1周期,直至稳定过程,且原型进入稳定周期时阻尼为190N·s/m,模型进入稳定周期时阻尼为899N·s/m,原型及模型非线性现象相同.

分别做出原型在阻尼190N·s/m、模型在阻尼899N·s/m时的稳态位移响应图,如图7所示.

图7　稳态位移响应值Fig. 7　The time history curves of the steady displacement

3.4响应随径向游隙变化

设原型计算初始参数：ω=10000r/min；C=300N·s/m；emp=0m；Mp=1kg；Fr=5N.则模型计算初始参数：ωm=λωωp=6768r/min;Cm=λCCp=1383.03N·s/m;Mm=λMMp=7.6540kg;Frm=λFrFrp=37.27N.

采用Newmark-β法求解原型及模型振动方程,可得出原型及模型随径向游隙变化速度分叉图,如图8所示.

图8　随径向游隙变化速度分叉图Fig. 8　Bifurcation diagrams: velocity-radial clearance relationships

对比图8可以看出,原型及模型均经历1周期-非周期-1周期,直至稳定过程,且原型进入稳定周期时径向游隙为13.3μm,模型进入稳定周期时径向游隙为40.5μm,原型及模型非线性现象相同.

分别做出原型在径向游隙14μm、模型在径向游隙41μm时的稳态速度响应图,如图9所示.

图9　稳态速度响应值Fig. 9　The time history curves of the steady velocity

由图2～9可以得出原型及模型非线性特性相关参数,对比原型、模型、模型预测原型的对应参数值,结果如表2所示.

由表2可以看出,模型能够准确预测出原型稳态响应值,进一步验证所推滚动球轴承非线性相似关系准确性.

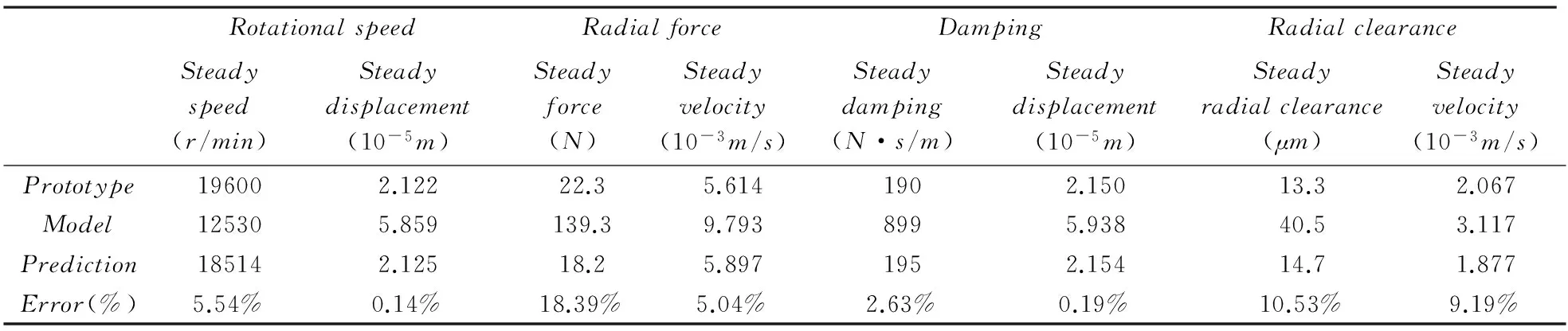
表2　原型、模型及模型预测参数值对比

4　结论

本文基于滚动球轴承系统振动方程,结合滚动球轴承动力学相似关系,推导出滚动球轴承系统相似关系,通过具体实例数值验证,可得出如下结论：

(1)滚动球轴承系统非线性振动相似关系与轴承自身结构参数相似关系之间存在一定的关系式；

(2)依据本文所推相似关系式建立的滚动球轴承系统相似模型能准确预测出原型系统的非线性现象及系统进入稳态状态下各参数数值及响应值.

1曹宏瑞,李亚敏,何正嘉等. 高速滚动轴承-转子系统时变轴承刚度及振动响应分析.机械工程学报, 2014,50(15):73～81 (CaoHR,LiYM,HeZJ,etal.Timevaryingbearingstiffnessandvibrationresponseanalysisofhighspeedrollingbearing-rotorsystems. Journal of Mechanical Engineering, 2014,50(15):73～81 (inChinese))

2李宏坤,赵利华,练晓婷.非线性刚度转子-轴承支承松动故障的特征分析.动力学与控制学报, 2011,9(3):233～237 (LiHK,ZhaoLH,LianXT.Characteristicsanalysisonnonlinearrigidrotor-bearingsystemwithpedestalloosenessfault. Journal of Dynamics and Control, 2011,9(3):233～237 (inChinese))

3ConstantinescuVN.Gaslubrication.NewYork：ASME,UnitedEngineeringCenter,1969

4杨茹萍,邓四二,李建华等.轴承组件轴承保持架放尺模型试验研究.航空动力学报, 2007,22(4):666～671 (YangRP,DengSE,LiJH,etal.Researchonbearingcagethroughexpanded-modeltest. Journal of Aerospace Power, 2007,22(4):666～671 (inChinese))

5杨丕珠,李彦,赵武等.变桨距回转轴承模型试验相似准则研究.机械设计与制造, 2008,(11):117～119 (YangPZ,LiY,ZhaoW,etal.Studyonthesimilaritystandardofthemodeltestforslewingbearing. Machinery Design and Manufacture, 2008,(11):117～119 (inChinese))

6姚世卫,王贤锋,张克龙等.舰船尾部轴承试验相似准则研究.舰船科学技术,2002,24(S1):53～57 (YaoSW,WangXF,ZhangKL,etal.Theresearchonshipsternbearingbyusingsimilaritystandard. Ship Science and Technology, 2002,24(S1):53～57 (inChinese))

7罗忠,陈晓兵,于清文等.轴承-转子系统中滚动球轴承的动力学相似设计.东北大学学报(自然科学版), 2013,34(9):1296～1299 (LuoZ,ChenXB,YuQW,etal.Dynamicsimilaritydesignofrollingballbearinginbearingrotorsystem. Journal of Northeastern University (Natural Science), 2013,34(9):1296～1299 (inChinese))

8YaoMH,ChenYP,ZhangW.Nonlinearvibrationsofbladewithvaryingrotatingspeed. Nonlinear Dynamics, 2012,68(4):487～504

9YaoMH,ZhangW.UsingtheextendedMalenkovmethodtostudymulti-pulsechaoticmotionsofarectangularthinplate. International Journal of Dynamics and Control, 2014,2(3):365～385

10YangXD,ZhangW.Nonlineardynamicsofaxiallymovingbeamwithcoupledlongitudinal-transversalvibrations. Nonlinear Dynamics, 2014,78(4):2547～2556

11HarshaSP.Nonlineardynamicanalysisofahigh-speedrotorsupportedbyrollingelementbearings. Journal of Sound and Vibration, 2006,290(1):65～100

12唐云冰,高德平,罗贵火. 滚动轴承非线性轴承力及其对轴承系统振动特性的影响. 航空动力学报, 2006,21(2):366～373 (TangYB,GaoDP,LuoGH.Nonlinearbearingforceoftherollingballbearinganditsinfluenceonvibration. Journal of Aerospace Power, 2006,21(2):366～373 (inChianese))

13SunnersjoCS.Varyingcompliancevibrationsofrollingbearings. Journal of Sound and Vibration, 1978,58(3):363～373

14YadavHK,UpadhyaySH,HarshaSP.Nonlineardynamicanalysisofhighspeedunbalancedrotorsupportedondeepgrooveballbearingsconsideringthepreloadeffect.In:ProceedingsofInternationalConferenceonAdvancesinTribologyandEngineeringSystems.SpringerIndia, 2014:481～490

15韩宝财,唐六丁,李云龙等.转子-滚动轴承系统非线性动力学分析.噪声与振动控制, 2008,28(4):20～23 (HanBC,TangLD,LiYL,etal.Nonlineardynamicsanalysisoftherotorrollingbearingsystem. Noise and Vibration Control, 2008,28(4):20～23 (inChinese))

16UpadhyaySH,JainSC,HarshaSP.Non-linearvibrationsignatureanalysisofahigh-speedrotatingshaftduetoballsizevariationsandvaryingnumberofballs. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, 2009,223(2):83～105

17周艳,张伟.复合材料层合板的双Hopf分叉分析.动力学与控制学报,2015,13(3):161～164 (ZhouY,ZhangW.Doublehopfbifurcationofcompositelaminatedthinplate. Journal of Dynamics and Control, 2015,13(3):161～164 (inChinese))

*TheprojectsupportedbytheNationalProgramonKeyBasicResearchProject(2012CB026005),theNationalScienceFoundationofChina(51105064,11572082),theFundamentalResearchFundsfortheCentralUniversitiesofChina(N150304004,N140301001)andtheKeyLaboratoryforPrecision&Non-traditionalMachiningofMinistryofEducation,DalianUniversityofTechnology(JMTZ201602)

†CorrespondingauthorE-mail:zhluo@mail.neu.edu.cn

14May2015,revised29June2015.

SIMILARITYRESEARCHONTHENONLINEARDYNAMICCHARACTERISTICSOFROLLINGBEARINGINROTOR-BEARINGSYSTEM†

LuoZhong1†GuoJian1TangRui1HanQingkai2WangDeiyou3

(1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang110819, China) (2. School of Mechanical Engineering, Dalian University of Technology, Dalian116023, China) (3. AVIC Shenyang Aero-engine Design Institute, Shenyang110042, China)

Asimilaritymodelconsideringthenonlineardynamiccharacteristicsofrollingballbearinginrotor-bearingsystemwasputforwardtoexaminetheproblemofdynamicsimilarity.Thenonlinearvibrationdifferentialequationofrollingballbearingwasfirstlyestablished.Thesimilarityrelationshiponthenonlineardynamiccharacteristicswasdeducedbytheintegralsimulationmethod,andthesimilaritydesigncriteriaoftherollingballbearingwasthenachieved.Afterwards,thegrooveballbearingofC204JUTand6208weresetasaprototypeandamodelfornumericalsimulation,respectively.Theeffectofrotationalspeed,radialloadFr,dampingCandradialclearanceonthevibrationdisplacementandvelocityofrollingballbearingsystemwereinvestigatedbybifurcation.Finally,throughcomparingthebifurcationrange,thestableparametervalue,theresponsevalueforthestablemotioninthebifurcationdiagram,thesimilaritycriteriawasverified.Theconclusionswereobtainedasfollow:i)Thesimilarityrelationshipofthenonlinearvibrationcharacteristicsfortherollingballbearingcanbeestablishedbyitsstructuralsimilarity.ii)Thebifurcationshapeoftheprototypeandthemodelwasconsistent,andthesteadyresponseofthemodelmatchedthatoftheprototypeverywell.

rotor-bearingsystem,rollingballbearing,nonlinearcharacteristics,dynamicsimilarity

E-mail:zhluo@mail.neu.edu.cn

10.6052/1672-6553-2015-050

2015-05-14收到第1稿,2015-06-29收到修改稿.

*国家重点基础研究发展计划项目(2012CB026005)、国家自然科学基金资助项目(51105064,11572082)、教育部基本科研业务费专项资金资助项目(N150304004,N140301001)及大连理工大学精密与特种加工教育部重点实验室研究基金资助项目(JMTZ201602)