气相色谱中粒子运动行为的随机行走模拟
郭 彦, 傅应强, 赵健伟
(1.南京信息工程大学环境科学与工程学院大气环境与装备技术协同创新中心,江苏南京 210044;2.南京大学化学化工学院,生命分析化学国家重点实验室,江苏南京 210093)
气相色谱在挥发性化学物质的分离、鉴定和定量分析上占有重要的地位,它在环境、工业、生物、法医等方面也有着突出的应用[1 - 3]。气相填充柱色谱是最早发展起来的色谱技术,相关色谱理论,如经典的速率理论、板高方程等也是最早被提出并完善的,在此基础之上色谱理论被进一步拓展到了开管柱以及液相色谱中。基于宏观的扩散理论,人们对气相色谱的保留值、半峰宽,色谱操作条件的优化已有大量的实验研究。在色谱理论的推进和深化过程中,从微观层面上对它的分离及条件控制的模拟也显得至关重要。譬如,Dondi等应用蒙特卡罗方法模拟了非线性色谱并优化了操作条件,并对Langmuir吸附模型相关的色谱热力学进行了研究[4]。Siepmann等应用蒙特卡罗方法研究了气液色谱中烷烃、醇、芳烃等物质的界面吸附、分配、保留机理等[5 - 7]。Tanaka等应用实验结合半经验量化计算的方法研究了氢/氘同位素在疏水作用上的影响[8]。Sun等运用分子动力学模拟了配体密度对蛋白质在疏水电荷诱导色谱上吸附、脱附和构型变化的影响[9]。Gorbunov等应用自编程的色谱二维可视模型研究了不同吸附作用下嵌段共聚物在液相色谱中的分配系数[10]。Sarti等应用数学模型描述了蛋白质在膜亲和色谱中的纯化过程[11]。这些理论研究为色谱实验提供了丰富的基础理论,然而,由于计算量的限制,这些理论研究主要集中在色谱热力学上,如吸附模型、两相分配等。
色谱在分离科学中占据不可或缺的地位也和它的动力学内容,如速率理论、流出曲线、待分离粒子的迁移过程等密不可分。色谱动力学不仅能促进提升色谱热力学研究的理论层次,而且能够对色谱分离的本质,操作条件的优化等起到关键性的指导作用。在理论层面上研究色谱动力学,就需要对整个色谱体系构建模型,繁复且计算量大。而随机行走特别适合用来模拟这种大规模体系。随机行走是Pearson在1905年引入的一项数学模型,用于描述在给定时间内连续且随机的运动轨迹[12]。随机行走最显著的优势在于它提取了运动行为中的关键性因素,并对其采取了适当且合理的近似,因而简化了计算量,使得随机行走能够运用在一些大规模的模拟体系中,如土壤和生物组织中的扩散问题[13,14]、药物输运[15,16]、神经传导[17]和晶体生长[18,19]等。
在气相色谱中,待分离粒子是限制在有限的空间环境内的,粒子与流动相间没有相互作用,它的运动行为跟随机扩散密切相关。基于这些相似性,我们应用随机行走模拟了气相填充柱色谱中待分离粒子的运动行为。同时,还开展了相对应的实际气相色谱实验。模拟与实验得出了相一致的结果,验证了本随机行走模型在气相色谱模拟上的可应用性。本模拟方法对于色谱操作条件的优化,及发展高效能色谱等具有参考价值。
1 计算方法与实验
1.1 计算方法
为了研究外部因素对保留因子,柱效等与色谱动力学相关参量的影响,我们采用了一种微观的随机模型用来描述填充柱色谱中分子运动的过程。所用软件为自主开发的随机行走程序,可在Window系统上运行[20 - 23]。
1.1.1分离柱分离柱定义为一个二维平面空间。根据实际实验中的色谱柱长,定义长度为2 m(X方向),宽度为2 mm(Y方向),见图1。在整个空间内,周期性排布着单元格,如图1中虚框所示。单元格中多边形为势垒,用来模拟色谱中的固定相。待分离粒子可以在这些空腔内(无势垒区域)自由运动,但不能进入这些势垒中。
1.1.2待分离粒子我们以忽略质量和体积的粒子(图1中的灰点)来模拟待分离粒子。粒子的位置用其所在单元格中的相对于单元格中心点的相对位置来描述:
Parrel=Parabs-Cellabs
(1)
其中,Parrel是粒子的相对位置对应的位矢,Parabs是粒子的绝对位置对应的位矢,Cellabs是势垒中心点的绝对位置对应的位矢。

图1 算法模型示意图。虚框为周期性排布的单元格,格内的绿色多边形代表着固定相。灰色圆点为待分离粒子,红色曲线为粒子的运动轨迹。桔色箭头和蓝色箭头分别代表着横向速度的方向和扩散速度的方向Fig.1 Schematic diagram of the simulated chromatographic system.The dashed box is the repeated arranged subcells,in which the green polygon represents the stationary phase.The grey dot is the point-like molecule,and the red curve is its’ mobile trajectory.The orange and the blue arrows represent the direction of transverse velocity and diffusion velocity,respectively
粒子的速度由两部分组成。一个是由驱动力施加的横向速度,定义为X方向的横向速度(Vx,单位为mm·s-1)。该速度可以用来代表实际实验中载气的流速。另一个速度是扩散速度,该速度是与温度相关的一个变量。在本文中该扩散速度的初始赋值是遵照气体布朗运动估算得出的。粒子扩散的运动方向随机生成,在以粒子为中心的0≤α<2π范围内等概率分布,α为方向角。粒子达到势垒边界上时,将按照弹性碰撞模型处理,即粒子的扩散速度大小不变,方向按照反射定律进行反射后继续在色谱柱中运动。
1.1.3运动过程粒子和势垒的相互作用可以用多种模型来描述,本模拟中采用弹性碰撞模型简化了粒子与固定相的作用。假定粒子在某段时间之内速度的方向和大小不发生变化,即速度和时间步(即粒子在程序中的行走时间单位与实际物理单位之间的比值,程序中采用0.005 s·step-1)决定了粒子一步随机行走的步长。在不受到势垒阻碍的情况下,根据速度、每步时间和粒子的当前位置即可确定粒子完成一步行走之后所处的位置。若粒子与势垒发生碰撞,它的横向速度不变,扩散速度大小不变,方向按照反射定律进行反射。时间也划分为两部分,分别为粒子运动到碰撞点前、后所需要的时间。碰撞前时间作用于碰撞前速度矢量,碰撞后时间作用与碰撞后速度矢量,据此可以确定碰撞之后的粒子运动轨迹。粒子若干个时间段内位置参数的时间积分,即可以确定整个时间段内粒子运动的轨迹:

(2)
1.2 色谱实验
高纯N2、高纯H2、空气和标准CH4(体积含量为3.2×10-6,剩余为Ar),均购买于南京红健气体有限公司。实验所使用的气相色谱仪为Agilent GC-6890N系统,配备氢火焰离子化检测器(FID)。填充柱为不锈钢材质,尺寸为2 m(X方向)×2 mm(Y方向),内填充固定相13XMS(载体粒径60~80目)。炉温和检测器温度分别设置为60 ℃和200 ℃。H2流速为30 mL·min-1,空气流速为400 mL·min-1。载气为N2,流速设为30 mL·min-1,在此载气流速下样品CH4气体的保留时间为2.05 min。每次实验以不分流的方式进样,进样体积均为10 mL。为了考察温度和压力的影响,实验中的炉温及载气流速会进行相应调整。
2 结果与讨论
2.1 粒子的扩散行为
为了评价模拟中粒子的扩散行为,分析了粒子的均方位移(MSD)。均方位移是指粒子位移平方的平均值,用来表征粒子运动性质的微观物理量,同时它也是一个受温度影响的物理量。在模拟程序中,均方位移定义为[24]:
(3)
其中,N代表粒子数目,t为时间,ri(t)-ri(0)为在t时间内的位移矢量。
如果以时间为横坐标,均方位移的斜率即为扩散系数D:
〈r2(t)〉=2dDt
(4)
其中,d是多维体系的维数。据此可以推导出在二维体系中扩散系数的表达式:
(5)
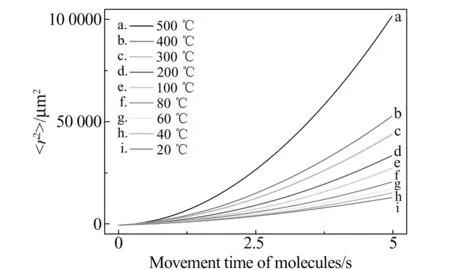
图2 不同温度条件下粒子的均方位移Fig.2 Mean square displacement under different temperature conditions
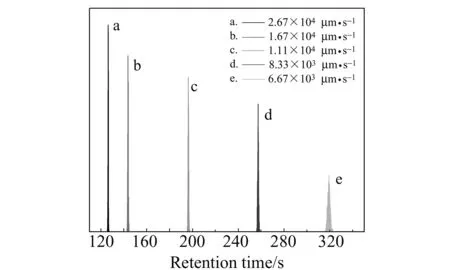
图3 不同横向速度条件下保留时间的柱状统计分布图Fig.3 Statistical distribution of the retention times with different transverse rates The particle size of stationary phase is 205 μm;temperature is 200 ℃.
图2为在不同模拟温度下,均方位移随时间的变化曲线。由图可见,当温度比较低的时候,粒子的均方位移随时间呈线性变化,说明粒子的自发运动是一个自由扩散的过程。从斜率上可以求出粒子的扩散系数。如,在温度20、40、60 ℃(曲线g、h和i)时,扩散系数分别为2.72×10-3、3.12×10-3和3.52×10-3mm2·s-1。这些数值与文献中报道的通过实验方法求解出的气体的扩散系数非常接近,均在同一个数量级内[25,26]。在模拟的温度区间内,当温度升高,均方位移随时间呈现曲线变化,说明除了扩散行为外,粒子还有具有明显的流动行为[27]。同时,曲线的曲率随着温度的升高而变大,表明扩散系数与温度之间应呈指数函数的变化关系。
2.2 压力影响
气相色谱对于压力变化比液相色谱更加的敏锐。在实际色谱实验中,如果压力增大,死时间和CH4气体的出峰时间会缩短。载气的流速由柱长和死时间计算得出。相应的,载气的流速随着压力的增大而增大。因而在模拟中,采用横向速度Vx作为压力大小的度量。Vx的取值设定是在实际实验结果的基础上,略有扩展而来。
图3为随着压力变化,粒子保留时间的柱状统计分布图。其中,温度固定为200 ℃,势垒粒径为205 μm。势垒粒径的设置也是根据实际实验中固定相载体的大小(60~80目)而定的。固定相填充率和形状等对粒子运动行为的影响可以参看我们以前的报道[22]。图3中,每个Vx条件下的柱状图都分别为1 000个粒子运动的统计结果。由图可见,这些柱状分布峰符合高斯正态分布,峰形光滑,无缺陷,且对称性好。压力增大势必引起横向速度的增加,因而在保留时间的统计图上,保留时间减小与预期结果相符,出峰时间从319 s缩短至126 s。值得注意的是,压力增大还引起了统计峰峰形的变化,峰形逐渐变窄变尖锐,说明柱效也相应增加。半峰宽(FWHM)是色谱流出曲线的一项重要参数,涉及到色谱动力学和组分分离方程。在其它条件不变的情况下,半峰宽的大小与柱效的高低成反比[28]。

图4 平均保留时间(a)和半峰宽(b)随横向速度的变化曲线;插图分别为各自相对应的实验结果Fig.4 The plots of the average retention time (a) and the full width (b) at half maximum versus the transverse rates;Insets are corresponding experimental results,respectively
图4为平均保留时间和半峰宽随Vx变化的曲线图,插图分别为相对应的色谱实验的结果。在实际色谱实验中,N2的压力只能在一定范围内调节,流速过大或过小都会使得检测器熄火。图4显示平均保留时间随着Vx的增大而指数衰减。压力增大,粒子受到的驱动力增加,通过色谱柱的时间也就越短。实验中当Vx从1.8×104增大到2.6×104μm·s-1时,出峰时间从175 s缩短至114 s。在相同Vx变化区间内,模拟结果从141 s缩短至127 s。模拟结果与实验结果基本一致。模拟中随着压力的增大,半峰宽先有个陡降的过程,再缓慢减小。而缓慢减小的区间与实际实验结果也是相吻合的。由于我们所采用的简化模型,忽略了两相间的分配平衡,所以模拟得出的半峰宽比实际结果要窄。根据速率理论,半峰宽减小的变化趋势说明无论是在模拟中还是在实验中,Vx都是设定在低流速区。半峰宽的减小对应于板高的减小,也就是柱效的增加。从模拟结合实验结果可知,在低流速区,我们可以通过施加一个适当的高压来缩短分析时间,提高柱效。
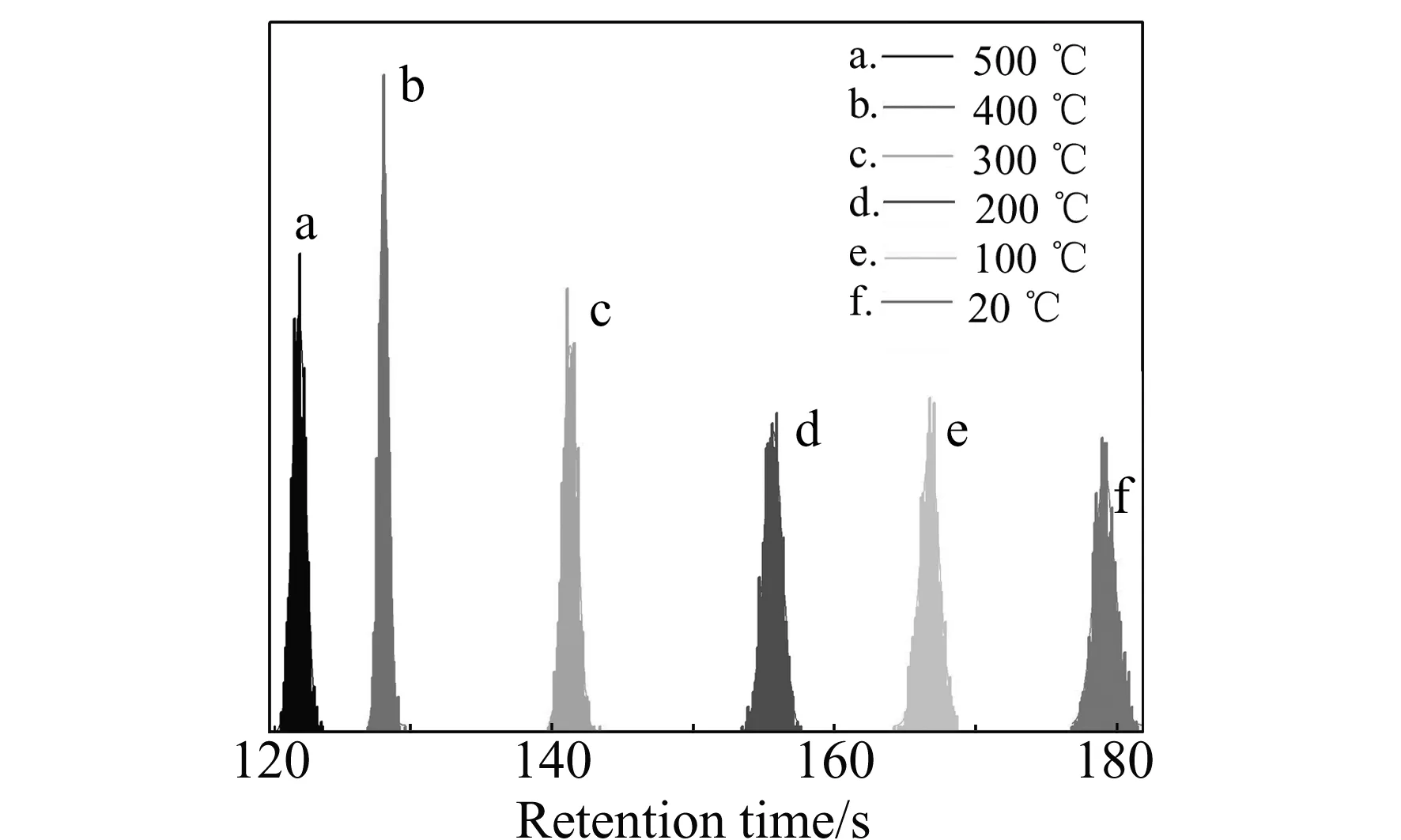
图5 不同温度条件下保留时间的柱状统计分布图Fig.5 Statistical distribution graph of the retention times with different temperature The particle size of stationary phase is 205 μm.The flow rate is 1.67×104 μm·s-1.
2.3 温度影响
在模拟程序中,温度的大小是由扩散速度反映,也就是分子的步速。温度与步速之间为线性关系,因而通过步速的调控来实现柱温的改变。图5为当固定相粒径和压力固定不变时,不同温度下粒子保留间的统计柱状图。峰形依然符合高斯正态分布。当温度升高,统计峰逐渐左移,出峰时间缩短。我们在图中观察到,随着温度的升高,统计峰先变窄变尖锐,温度继续升高,峰形又会展宽。
图6为平均保留时间和半峰宽随温度变化的曲线图。插图分别为相对应的色谱实验的结果。在实际色谱实验中,为了保证体系的稳定性和避免固定液的流失,温度只能在小范围内调节(小于140 ℃)。由图6可见,在实验的温度变化区间60~140 ℃内,保留时间从123 s 缩短至 82 s。相同区间内,模拟结果从173 s缩短至161 s。无论是模拟还是实验结果,保留时间均随着温度的升高而指数级衰减的。对于半峰宽而言,实验结果也是单调递减的,但模拟结果给出先减小后增大的变化趋势。这可能是由于温度不仅影响着扩散速度,也影响着扩散系数,扩散系数对于板高的影响本身就是一个复杂的变量。在与实际实验相同的温度区间,半峰宽的变化是一致的。半峰宽在模拟结果中给出了一个最小值,也就是在427 ℃左右可以获得最高柱效。

图6 平均保留时间(a)和半峰宽(b)随温度的变化曲线;插图分别为各自相对应的实验结果Fig.6 The plots of the average retention time (a) and the full width (b) at half maximum versus the temperature;Insets are corresponding experimental results,respectively
在气相色谱中,温度是一个相对复杂的影响因素,它在选择性、分子扩散及柱效之间构建了一个平衡。从模拟结果可以看出柱温对于柱效的影响并不是单调变化的。如果在实际实验中想提升柱效,可以在低流速区施加一个适当的高温。同时,模拟结果给出了最佳柱效的温度条件。尽管由于实际操作条件的限制,我们不能此温度下运行色谱柱,但是这对于其它色谱体系操作条件的选择还是具有一定的参考意义。
3 结论
待分离粒子的动力学行为在气相色谱的研究中至关重要,它能够影响色谱动力学的一些基本内容,如van Deemter方程、Giddings方程、分离过程等。本文中运用自主开发的随机行走软件对气相填充柱色谱中的运动行为展开模拟,并考察了温度和压力因素的影响。同时,我们也在实际气相色谱实验中考察了这两项影响因素。从模拟与实际实验中我们得出了相一致的结果。由于实际实验操作条件的限制,模拟结果给出了一个更宽泛的应用区间。通过随机行走模拟,我们可以从分子层面对气相色谱中分子的运动行为给出合理解释,并能够实现操作条件的优化。

