含铁基纳米晶带线圈与电容LC混联电路的谐振频率

王宗篪，张晓玉，黄思俞，郑冬梅

（三明学院 机电工程学院，福建 三明 365004）

含铁基纳米晶带线圈与电容LC混联电路的谐振频率

王宗篪，张晓玉，黄思俞，郑冬梅

（三明学院 机电工程学院，福建 三明 365004）

含有Fe73Cu1Nb1.5V2Si13.5B9纳米晶带的电感线圈与电容Cs串联再与电容Cp并联，组成仿石英晶体振荡电路。通过实验发现，含铁基纳米晶带线圈与电容LC混联电路有3个谐振频率，一个串联谐振频率，另一个并联谐振频率，还有第3个谐振频率。把实验分别测出含铁基纳米晶带线圈自感系数Ls、铁基纳米晶带交流磁化损耗的等效电阻Rs与交流磁化场频率f的关系曲线进行数值拟合，得到Ls、Rs与频率f的函数式，再带入含铁基纳米晶带线圈与电容LC混联电路的复阻抗表达式中，用数值解法得到谐振时有3个正实根，说明了实验测得含铁基纳米晶带线圈与电容LC混联电路有3个谐振频率的结果。当外磁场作用在含铁基纳米晶带上时，含铁基纳米晶带线圈与电容LC混联电路串联谐振频率和并联谐振频率向高频移动，而第3个谐振频率不发生变化，通过实验测得自感系数和损耗电阻在谐振频率时随外磁场的变化关系解释了上述现象。

铁基纳米晶带；LC混联电路谐振；谐振频率；曲线拟合；磁致频移

巨磁阻抗效应（giant magneto-impedance effect，简称GMI），是指软磁材料的交流阻抗在外加直流磁场的作用下发生显著变化的现象［1］。这种效应具有高灵敏度、响应快等特点，在磁场、位移等传感器以及磁记录方面有着广泛的应用前景［2-4］。近年来，人们在测量电路中并入了电容或在软磁材料中加入绝缘层构造电容，组成了LC共振回路，在共振的频率附近出现了显著的GMI共振增强［5-12］。研究其LC共振型GMI效应，有助于开发新的LC电路共振器件，这将在调制、解调、滤波、振荡等自动控制电路得到广泛应用。

石英晶体振荡器具有高Q值和高频率稳定度，因此得到了广泛应用。石英晶体振荡器可以等效成LC混联电路如图1所示，它有两个固有谐振频率，串联谐振频率fs和并联谐振频率fp，石英晶体振荡器的电抗特性如图2所示［13］。本工作把含铁基纳米晶带电感线圈与电容Cs串联再与电容Cp并联，组成仿石英晶体振荡电路，如图3所示。实验发现，含铁基纳米晶带线圈与电容LC混联电路有3个谐振频率，一个串联谐振频率fs，另一个并联谐振频率fp，还有第3个谐振频率ft。把实验测出含铁基纳米晶带线圈自感系数Ls、铁基纳米晶带交流磁化损耗的等效电阻Rs与频率的关系曲线，进行数值拟合，得到 Ls、Rs与频率f的函数式，再带入含铁基纳米晶带线圈与电容LC混联电路的复阻抗表达式中，用数值解法得到谐振时有3个正实根，对应实验测得的3个谐振频率。当外磁场作用在含铁基纳米晶带上时，串联谐振频率和并联谐振频率向高频移动，而第3个谐振频率不发生变化，通过实验测得自感系数和损耗电阻在谐振点时随外磁场的变化解释了上述现象。

图1　石英晶体振荡器的等效电路

图2　石英晶体振荡器的电抗特性

图3　含铁基纳米晶带线圈与电容混联振荡电路

1　实验

实验采用日置公司生产的3535LCRHITESTER测量仪，该仪器的频率测试范围是100 KHz～120 MHz，可以测量的物理量包括电路中阻抗Z、电抗X、电阻R和阻抗角θ、电感L、电容C等。

从图3可看出，当Cs很小时，由可知，串联支路Z1很大，整个电路的总阻抗由并联支路的阻抗Z2决定，无法产生LC混联电路共振。当Cp很大时，由可知，并联电路阻抗Z2很小，整个电路的总阻抗由并联电容Cp支路的阻抗Z2决定，也无法产生LC混联电路共振。综上可知，只有当Cs足够大，Cp足够小时，才可以产生LC混联电路共振。通过实验测得，0.4时，含铁基纳米晶带线圈与电容LC混联电路可以产生谐振。取F ，即=时，讨论含铁基纳米晶带线圈与电容LC混联电路的谐振特性。

2　实验结果

不加外磁场，把含铁基纳米晶带线圈与电容LC混联电路接入3535LCRHITESTER测量仪，测得含铁基纳米晶带线圈与电容LC混联电路阻抗角θ、阻抗Z、电抗X随交变电流频率f的变化关系，分别如图4～6所示。

不加外磁场，把3535LCRHITESTER测量仪接入含铁基纳米晶带线圈的两端，测得铁基纳米晶带线圈自感系数Ls、铁基纳米晶带交流磁化损耗的等效电阻Rs随交变电流频率f的变化关系，分别如图7～8所示。

图4　含铁基纳米晶带线圈与电容LC混联电路阻抗角随频率的变化关系

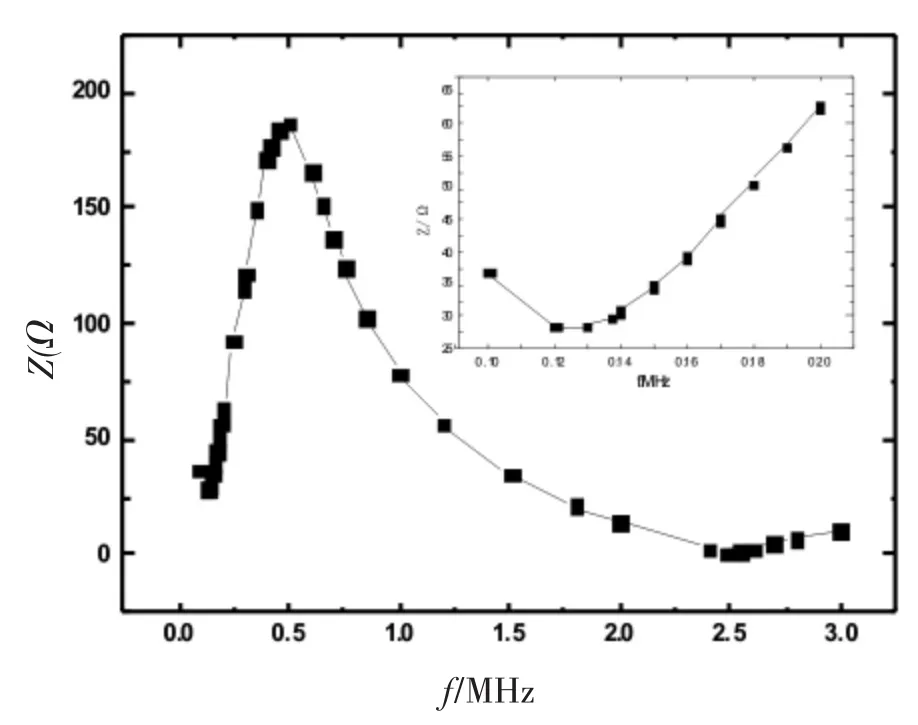
图5　含铁基纳米晶带线圈与电容LC混联电路阻抗随频率的变化关系

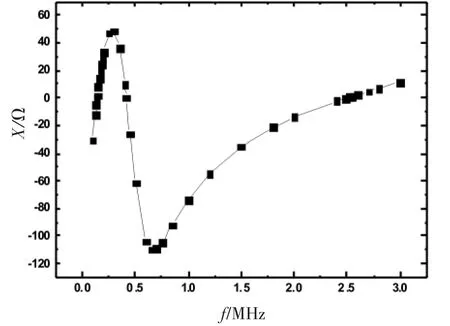
图6　含铁基纳米晶带线圈与电容LC混联电路电抗随频率的变化关系

图7　自感系数Ls随频率f的变化关系

图8　损耗等效电阻Rs随频率f的变化关系

图9　谐振频率随外磁场的变化关系

加上外磁场，用3535LCRHITESTER测量仪实验测出含铁基纳米晶带线圈与电容LC混联电路3个谐振频率随外磁场变化关系，如图9所示。当驱动电流频率分别为fs、fp和 ft时，实验还测出铁基纳米晶带线圈自感系数Ls、铁基纳米晶带交流磁化损耗的等效电阻Rs随外磁场变化关系，如图10～11所示。

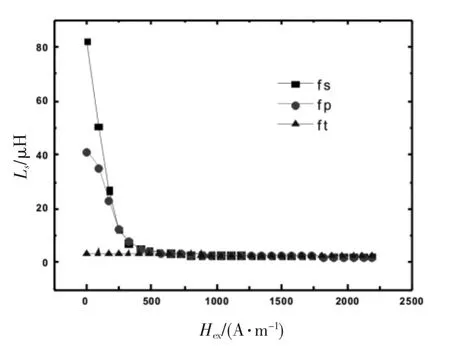
图10　对应3个谐振频率下自感系数随外磁场的变化

图11　对应3个谐振频率下损耗等效电阻随外磁场的变化

3　分析讨论

3.1含铁基纳米晶带线圈与电容混联电路谐振频率问题

与石英晶体振荡器只有两个谐振频率不同，由图4可看出，实验得出含铁基纳米晶带线圈与电容LC混联电路有3个谐振频率，第1个谐振频率为fs=137.2 kHz，第2个谐振频率为fp=415 kHz，以及第3个谐振频率为ft=2.489 MHz。

由图5可以看出，在第1个谐振频率附近，阻抗取得极小值Zmin=28.44 Ω，LC混联电路属于串联谐振。在第2个谐振频率附近，阻抗取得极大值Zmax=186.5 Ω，LC混联电路属于并联谐振。在第3个谐振频率处，即在ft=2.489 MHz时，阻抗取得极小值Zmin=0.704 Ω，LC混联电路也属于串联谐振。通过图6可知，在频率为fs=137.2 kHz时，电抗X=0.020 Ω。在频率fp=415 kHz时，电抗X=0.101 Ω。在频率时ft=2.489 MHz，电抗X=0.005 Ω。在3个谐振频率处，电抗很小，几乎为0。

由图7可知，自感系数Ls随频率f的增大而单调减少，Ls不是常数，它是频率的函数。由图8可知，Rs也不小且不是常数，它也是频率的函数。Rs随频率的变化，先增大后减小，在f=450 kHz时，取得最大值Rs=213.4 Ω，在f=1.5～3 MHz范围内，Rs随频率的变化已很小了。在交流磁化中，铁磁材料的磁导率要用复数μ~=μ'-iμ''表示，μ~的实部μ'称为弹性磁导率，与静态磁化时的磁导率相当，它是一个实数，表示在动态磁化过程中单位体积铁磁体储存的磁能，μ~的虚部μ''又叫粘滞性磁导率，它决定于在交变磁场中单位体积的铁磁体每磁化一周损耗的磁能［15］。对于铁磁材料磁谱：f在104～106Hz间，μ'随f持续减小，μ''则随f先急剧增大，在某个频率f*处，μ''出现峰值，大于频率f*，μ''随f急剧减小；f在106～1010Hz间，μ'随f缓慢下降，最后变化很小，μ''随f缓慢下降，最后也变化很小［16］。对于含铁基纳米晶带的长螺线管线圈，它的自感系数，自感系数与磁导率成正比。因为，式中为螺线管空心线圈的自感系数［15］，所以，Ls∝μ'，Rs∝μ''。自感系数Ls随频率f的变化与复数磁导率实部磁谱相当，损耗等效电阻Rs随频率f的变化与复数磁导率虚部磁谱相当。因此，图7和图8分别显示Ls和Rs的频谱，是由长螺线管内铁基纳米晶带纵向磁化磁导率的磁谱决定的。

含铁基纳米晶带线圈与电容LC混联电路与石英晶体振荡器等效电路形式相同，都是由电感线圈Ls、电容Cs和损耗电阻Rs串联再与电容Cp并联组成。两种LC混联振荡电路复阻抗都可以表示如式（1）：

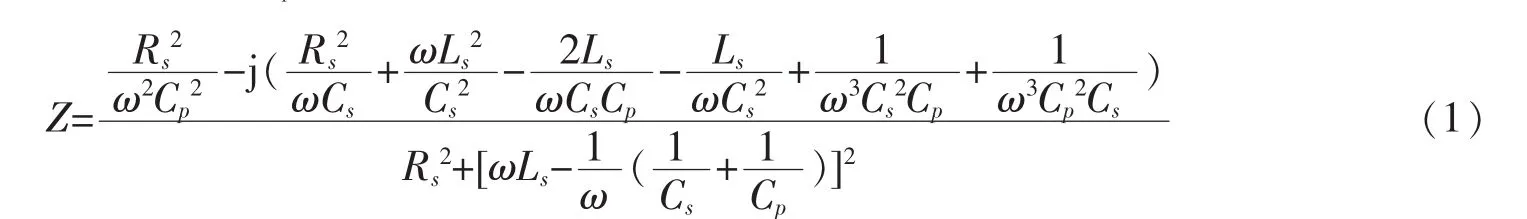
当LC混联电路发生谐振时，阻抗角θ=0°，（1）式的虚部等于0，可以得到以下方程

整理，可得：

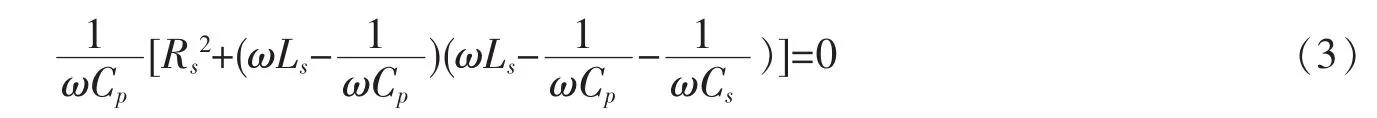
对于石英晶体振荡器，Ls是常数，Rs很小可不计，所以（3）式可化为

对于含铁基纳米晶带线圈与电容LC混联电路，Ls不是常数，它是频率的函数，Rs也不小且不是常数，它也是频率的函数，不能略去不计。因此，要得到（3）式的解，先要分别找出Ls与频率、Rs与频率的函数解析关系，再把Ls（f）、Rs（f）代入（3）式，求出（3）式的正实数解，几个正实数根就表示含铁基纳米晶带线圈与电容LC混联振荡电路有几个谐振频率。

把实验测得自感系数Ls与频率f的关系，利用Origin软件具有多项式拟合的功能，拟合出自感系数Ls与频率f的函数关系式，图12为实验曲线与拟合曲线的相近程度。

拟合出的自感系数Ls与频率f的九次方的函数表达式为：

拟合出的R-Square为：0.99997（当R-Square的值越接近1，表示拟合效果越好）

把实验测得损耗等效电阻Rs与频率f的关系，利用Origin软件，拟合出了损耗等效电阻Rs与频率f的函数关系式，图13为实际曲线与拟合曲线的相近程度。

拟合出的损耗等效电阻Rs与频率f的九次方函数表达式为：

拟合出的R-Square为：0.98575（当R-Square的值越接近1，表示拟合效果越好）。

图12　实测自感系数Ls频谱曲线与拟合曲线　

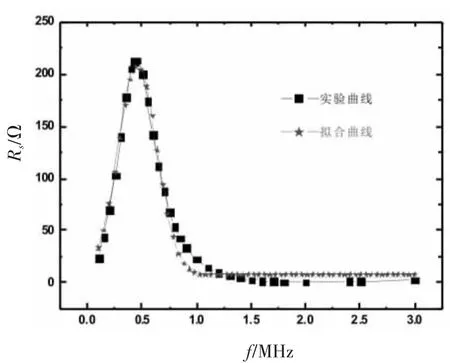
图13　实测损耗等效电阻Rs频谱曲线与拟合曲线

把（5）、（6）式代入（3）式，其中Cs=2×10-8F，Cp=2×10-9F，ω=2πf，频率f的单位为MHz，利用Matlab软件，可计算出（3）式方程的根为：3.0048±0.0251i，2.6294±0.1650i，2.3458±0.3347i，1.9201±0.4046i，1.4585±0.4018i，1.4412±60.2596i，1.2237，0.9893±0.3720i，0.6384，0.3631，0.0820±0.1546i，-0.0128。

有3个实根，分别为：f1=363.1 kHz，f2=638.4 kHz，f3=1.2237 MHz，以及1个负根，其它为复共轭根。负根与复共轭根无意义，舍去。用数值解法得到3个正实根，即含铁基纳米晶带线圈与电容LC混联电路有3个谐振频率，它与实验测得结果对应。

通过实验测得的3个谐振频率，大小分别为：fs=137.2 kHz，fp=415 kHz，ft=2.489 MHz。数值计算得到3个谐振频率分别为：f1=363.1 kHz，f2=638.4 kHz，f3=1.2237 MHz。实验结果和数值解有误差，这主要是数值拟合误差造成的。从图13可看出，f在0.8～1.2 MHz区间损耗等效电阻Rs的拟合曲线与实验曲线存在的拟合误差，使得谐振频率实验测量值与数值计算值有偏差，但都只有3个谐振频率，在这方面实验结果和数值计算结果是一致的。

3.2外磁场对含铁基纳米晶带线圈与电容混联电路谐振频率的影响

图9是含铁基纳米晶带线圈与电容LC混联电路谐振频率随外磁场的变化情况。由图9可见，串联谐振频率和并联谐振频率均发生了磁致频移，而第3个谐振频率不随外磁场变化。

串联谐振频率和并联谐振频率出现磁致频移而第3个谐振频率基本不随外磁场变化的原因，可以用由实验测出自感系数Ls和损耗等效电阻Rs随外磁场变化关系（见图10～11）来说明。由图10～11可看出，在串联谐振频率和并联谐振频率下自感系数Ls和损耗等效电阻Rs随外磁场增大而单调急剧减小，当外磁场增大到一定值后，自感系数Ls和损耗等效电阻Rs随外磁场缓慢变化直至趋于定值，在第3个谐振频率下自感系数Ls和损耗等效电阻Rs随外磁场增大而基本没有变化。因为，fs∝1/，所以，串联谐振频率和并联谐振频率出现磁致频移而第3个谐振频率基本不随外磁场变化。

4　结论

（1）把实验测出含铁基纳米晶带线圈自感系数Ls和铁基纳米晶带交流磁化损耗的等效电阻Rs与频率的关系曲线，进行数值拟合，分别得到Ls、Rs与频率f的函数式，再带入含铁基纳米晶带线圈与电容LC混联电路的复阻抗表达式中，用数值解法得到谐振时有3个正实根，数值计算说明了含铁基纳米晶带线圈与电容LC混联电路有3个谐振频率，解释了含铁基纳米晶带线圈与电容LC混联电路实验测得3个谐振频率的结果。

（2）实验发现，外磁场沿纵向加在含铁基纳米晶带上，含铁基纳米晶带线圈与电容LC混联电路的串联谐振频率和并联谐振频率发生了变化，即磁致频移，串联谐振频率和并联谐振频率随外磁场增大向高频方向移动，最后趋于饱和，而第3个谐振频率不发生磁致频移。实验测得自感系数和损耗等效电阻在谐振频率时随外磁场的变化关系解释了上述现象。

［1］MOHRI K，KOVHZAWA T，KAWASHIMA K，et al.Magneto-inductive effect（MI effect）in amorphous wires［J］. IEEE Trans Magn，1992，28（5）：3150-3152.

［2］蒋峰.非晶带巨磁阻抗效应磁场测量仪［J］.功能材料与器件学报，2014，20（5）：164-169.

［3］邵思奇，孙亚娟，张树玲，等.CoFeSiB非晶丝弱磁场测量仪的研制［J］.大学物理实验，2015，28（1）：1-4.

［4］王红洲，郑金菊，郑建龙，等.基于铁基非晶薄带巨磁阻抗效应的位移传感器［J］.传感器与微系统，2015，34（7）：88-90.

［5］王宗篪，黄丽斌.铁基多层膜连接等效成LC并联电路的巨磁阻抗效应［J］.漳州师范学院学报（自然科学版），2012，25（2）：53-56.

［6］程金科，潘海林，赵振杰，等.LC共振型复合结构丝的高频巨磁电抗效应［J］.科学通报，2007，52（22）：2603-2606.

［7］潘海林，程金科，赵振杰，等.LC共振型巨磁阻抗效应的研究［J］.物理学报，2008，57（5）：3230-3236.

［8］KIM Y S，YU S C，LEE J B，et al.A New class of LC-resonator for micro-magnetic sensor application［J］.Magn Magn Mater，2006，304：117-121.

［9］RAPOSO V，VAZQUEZ M，FLORES A G，et al.Giant magneto-impedance effect enhancement by circuit matching［J］. Sens Act A，2003，106：329-332.

［10］LEAT，KIMCO，PHANMH，etal.Verylargemagneto-impedanceeffectinaglass-coatedmicrowireLC-resonator［J］.Phys B，2007，395：88-92.

［11］LE A T，CHO W S，KIM Y S，et al.A micro-LC-resonator fabricated by MEMS techenique for high-frequency sensor applications［J］.Sens Act A，2007，135：547-551.

［12］何家康，袁望治，程金科，等.CoP/Insulator/BeCu复合结构丝的巨磁阻抗效应研究［J］.功能材料，2008，11（39）：1813-1816.

［13］武汉大学《电子线路》教材编写组.电子线路：下册［M］.北京：人民教育出版社，1979：32-34.

［14］杨燮龙，杨介信，陈国，等.一种新型的纵向驱动巨磁阻抗效应［J］.科学通报，1997，42（3）：257-259.

［15］宛德福，马兴隆.磁性物理学［M］.成都：电子科技大学出版社，1994.

［16］廖绍彬.铁磁学：下册［M］.北京：科学出版社，1998：65.

（责任编辑：朱联九）

The Resonant Frequencies of the LC Series-parallel Circuit Composed of Capacitors and a Coil which Containing Fe-based Nanocrystal Ribbons

WANG Zong-chi，ZHANG Xiao-Yu，HUANG Si-yu，ZHENG Dong-mei
（School of Electromechanical Engineerig，Sanming University，Sanming 365004，China）

In this study， the bionic quartz crystal oscillation circuit was composed of a inductance coil which containing Fe-based nanocrystal ribbons in series with a capacitor Csand then in parallel with a capacitor Cp. Three inherent resonant frequencies were found in bionic quartz crystal oscillation circuit through experiments， one series-resonant frequency fs， another parallel-resonant frequency fp， the third resonant frequency ft. The frequency dependence of the self inductance Lsof the coil which containing Fe-based nanocrystal ribbons and the equivalent resistance Rsof the hysteresis loss of Fe-based nanocrystal ribbons were measured， respectively， Ls=Ls（f）and Rs=Rs（f）were obtained by fitting the curve of the frequency dependence of the Lsand Rs， respectively. Ls=Ls（f）and Rs=Rs（f）were substituted into the complex impedance Z expression of the LC series-parallel circuit composed of capacitors and a coil which containing Fe-based nanocrystal ribbons， three real roots of the equation of Im（Z）=0 were obtained by numerical solution when the resonant of the LC series-parallel circuit composed of capacitors and a coil which containing Fe-based nanocrystal ribbons， and corresponding to the experimental phenomenon of three inherent resonant frequencies of the LC series-parallel circuit composed of capacitors and a coil which containing Fe-based nanocrystal ribbons. The dependence of the LC series-parallel circuit cmposed of capacitors and a coil which containing Fe-based nanocrystal ribbons resonant frequencies on external magnetic field were measured， the phenomenon of the magnetic frequency shift of the LC series-parallel circuit composed of capacitors and a coil which containing Fe-based nanocrystal ribbons were explained according to the external magnetic dependence of the self inductance of the coilwhich containing Fe-based nanocrystal ribbons and the equivalent resistance of the hysteresis loss of Fe-based nanocrystal ribbons through experiments at three inherent resonant frequencies， respectively.

Fe-based nanocrystal ribbons； LC series-parallel circuit resonance； resonant frequency； fitted curves plot；magnetic frequency shift

TM131.41

A

1673-4343（2016）04-0047-07

10.14098/j.cn35-1288/z.2016.04.009

2016-05-03

福建省省属高校科研专项（JK2010060）

王宗篪，男，福建永安人，教授。主要研究方向：磁性材料。