数据锁存处理的低误码率编码方法研究

吴 金 江 琦 郑丽霞 孙东辰 宋 科 孙伟锋



数据锁存处理的低误码率编码方法研究

吴 金①江 琦②郑丽霞*①孙东辰②宋 科②孙伟锋②

①(东南大学无锡分校 无锡 214135),②(东南大学集成电路学院 南京 210096)

对于时间信号量化后的数字编码处理，传统编码方法高频条件下存在高误码率导致数据量化精度退化的问题。该文从数据误码根源分析入手，建立起不同状态模式下包含锁存和延迟失配效应的误码解析分析模型，并在二进制和格雷码编码方法对比的基础上，分析了低误码率的同频码编码设计方法。基于TSMC 0.35mm CMOS工艺，完成了采用同频码编码方法的时间数字转换器(TDC)电路及其版图设计，多项目晶元(MPW)芯片的测试结果表明：同频编码的误码率相比同等条件下传统编码方法的误码率明显降低，并与理论分析基本吻合。

编码电路；时间数字转化器；误码率；数据采样

1 引言

时间数字转换器(Time-to-Digital Converter, TDC)可将两个异步信号定义的时间间隔模拟量转换为二进制数字量。时间测试量程与量化分辨率作为TDC的关键指标,在大阵列应用条件下因寄生效应的影响而明显退化。对被测时间的非理想采样与编码操作，显著增加了转换过程中的非线性误差[4,5]。因此，为了抑制TDC有效转换位数的退化，必须在状态采样和数据编码处理过程中找到抑制误码的有效方法。TDC的基本量化单位通常直接或间接来自于计数时钟信号[6]，时钟频率的变化将直接引起状态采样的误码；对于频率稳定的计数时钟，触发器的非理想建立保持时间[7]，同样可引入状态锁存误码。电路系统中的各类非理想因素正是通过对计数时钟频率和逻辑电路延迟特性的影响，使系统量化分辨性能明显偏离理想本征特性。

为简化分析，本文仅考虑在时钟频率稳定条件下的误码问题及误码抑制方法。一般数字电路系统中的数据采样均可通过采样时钟信号与数据时序的配合，即采样时充分避开触发器建立保持时间有效作用区域而避免误码。但在TDC应用中，由于采样时钟信号与有效数据之间时序关系的随机性，非理想采样引起的误码无法避免。此外，对采样状态的非理想编码也会引入多路编码数据之间相对关系的变化而产生误码。在二进制编码电路中，由传输路径延迟失配引起的误码，最低编码位因其频率最高，误码率最大。二进制编码状态变化时，编码中多位数据同时发生翻转，产生很大的尖峰脉冲，噪声特性的退化又进一步增大了误码风险[8]。目前，对于TDC应用中数据转换误码模型仍缺乏系统研究，本文通过对误码根源的分析，提出了针对随机性数据非理想采样与编码的误码分析模型，在此基础上给出了抑制误码的优化方法及相应的编码电路设计方案。

2 误码产生根源

在上升和下降沿延迟均为零的理想稳定时钟条件下，对于频率为的周期数据信号，其误码率定义为一个周期内数据错误时间段t所占的比重，即

数据采样过程中误码有两种不同性质的来源，分别对应数据锁存误码和数据编码误码。当随机到来的数据锁存信号触发沿与数据信号跳变沿之间的时间间隔小于触发器的建立保持时间时，数据采样出错[9]。这种由触发器固有的建立保持时间引入的错误采样为数据锁存误码，以1表示。实际非理想触发器无法完全消除此类误码，只能通过减小建立保持时间以及降低采样频率的方式加以抑制。在对多相时钟各状态节点的编码过程中，扇入数量不同、输出逻辑路径不匹配以及节点负载差异等因素，导致相对延迟偏差并改变数据之间正常的相位关系，由此引入的数据编码误码，以2表示。非理想编码误码率的降低或消除依赖于电路延迟匹配性能的改善。

触发器建立保持时间产生的固有锁存误码，其本质是对正确数据的错误锁存，决定了系统所能达到的最小误码率；延迟失配引入的编码误码与不同信号沿之间的相互位置关系密切相关，涉及最小公倍周期的确定等问题，其实质是对错误数据的正确锁存。若两种不同性质的误码源独立无关，则可分别计算1和2，并利用线性叠加原理计算总的误码率，即=1+2。若引入的两类误码信号相关，则需找出两者的最小公倍数周期，将两个相关信号等效成一个复合信号，分别考察锁存和编码误码率，并按照等效单周期内的误差状况叠加得到完整误码率，总误码率小于相互独立的两种误码源直接叠加的结果，即。在极特殊状态下，若两种误码同时发生，双重误码可恢复到非误码，其实质是对错误数据的错误锁存得到正确的数据。为简化模型分析可忽略低概率事件，并可用最大误码率1+2估算最差条件下的总误码率。

3 误码模型

为正确锁存数据，触发器锁存时刻之前数据稳定不变的最小时间应大于触发器的建立时间t，而保持时间t决定了触发器锁存时刻之后，数据需维持稳定不变的最小时间。输入数据需在触发器锁存时刻之前与之后的建立保持时间sh内维持稳定不变，才能正确锁定数据，其中sh=t+t，此类固有误码率可以由sh占时钟周期信号的比重近似估算。在此基础上，增加编码误码模型，再根据两者不同关联特性以特定方式叠加可以得到完整的误码模型。

3.1 数据跳变沿近似对齐的误码模型

以两位二进制编码为例，编码数据周期信号1和2的频率分别为1和2,sr和hr分别表示针对高电平锁存的建立及保持时间，sf和hf分别表示针对低电平锁存的建立及保持时间；触发器建立(或保持)时间可取其高、低电平建立(或保持)时间的平均值。若编码数据跳变沿之间的时间间隔充分靠近并小于sh，即边沿非严格对齐，1和2的误码时间段存在部分重合，各自的固有误码不再相互独立，有效误码率低于各自独立误码率的线性叠加，即

根据图1给出的数据采样时序关系，若1和2上升沿间距为1，低频信号2下降沿与1上升沿间距为2，则高频信号1的锁存误码率为sh´1；由于2上升沿与1跳变沿之间存在交叠的建立保持时间，所以2引起的建立保持时间有效作用范围增加了1+2，即锁存误码率增加了(1+2)/，其中取两信号的最小公倍周期，则对于数据跳变沿近似对齐的两路编码信号其总误码率为

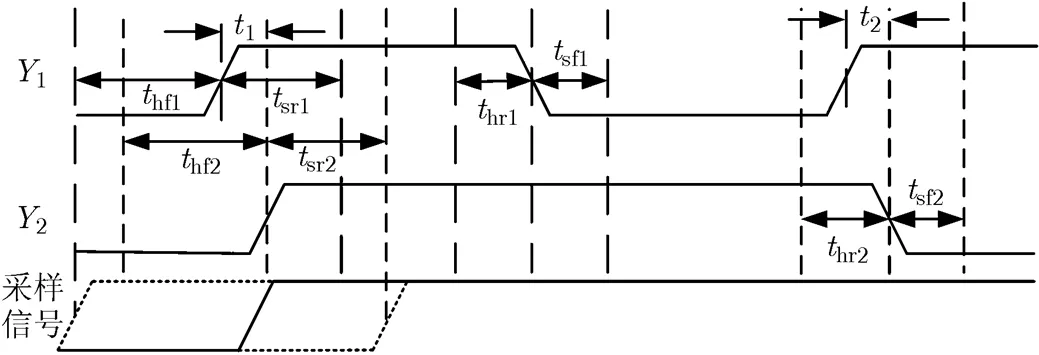
图1 相邻二分频数据采样的时序关系图

显然，以上总误码率仍满足式(2)给定的约束条件，且式中第1项为触发器锁存单路高频信号的固有锁存误码，对于多位编码的误码率，由数据变化频率最高的权重位决定；第2项给出了两路二进制编码细微延迟失配下低频数据位锁存对总误码的贡献。降低各路编码信号的频率，采用低建立保持时间的触发器，减小各路数据跳变沿之间的细微延迟差异是降低数据锁存误码率的基本方法。若式(3)中1=2=0，则总误码率仅来自于高频数据的锁存误码，边沿严格对齐可将各路间失配对误码率附加的影响降为0，以上两路编码可推广到多级二进制编码输出模型。当二进制编码中任意两位数据跳变沿的间距大于建立保持时间，则需要采用3.2节数据跳边沿非对齐模型进行相关误码率的计算。

3.2 数据跳变沿非对齐的误码模型

对于其它非二进制编码方法，通常其相邻两位编码输出信号的边沿间距远大于建立保持时间，满足边沿无交叠条件；若1和2频率相同，初始沿不交叠必然导致信号相位交错且不会再交叠；1和2频率如存在整数倍关系，初始边沿错位，且错位的相位差小于各编码输出的最小周期，两路信号之间仍然不会出现边沿交叠。在此重复周期内，仅需计算各自数据通路的锁存误码率，叠加后得到总的锁存误码率。将以上两信号关系推广到无边沿交叠的多位编码输出状态，得到由锁存误码决定的总误码率为

对于跳变沿非交叠的编码方法，两路交错信号之间延迟失配产生的编码误码，可用图2定性说明。1和2为理想无延迟编码输出，和为有延迟的实际编码输出，与1和2的相对延迟分为上升沿延迟dr1和dr2，以及下降沿延迟df1和df2。若仅编码输出有延迟，触发数据锁存的采样信号没有延迟，在编码数据的相对延迟时间内，实际编码数据与理想状态相反，即对错误数据的正确锁存形成误码。在一个周期内，两组信号相对延迟构成的误码总时间为t=dr1+df1+dr2+df2。由于非交叠下各路信号引起的编码误码相互独立，根据独立原则计算各自周期内的误码并叠加，则总的编码误码率为

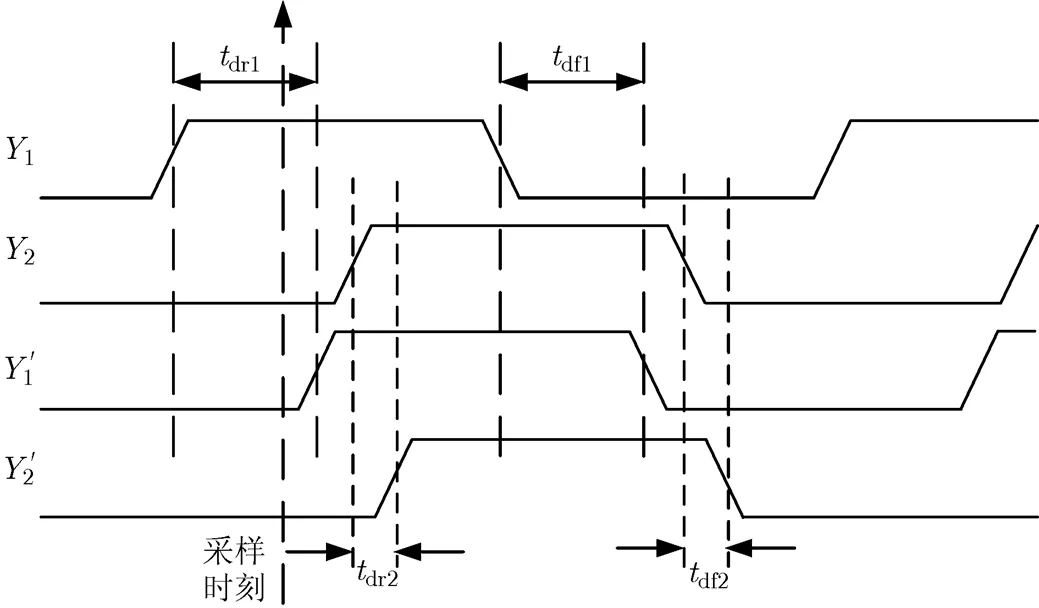
图2 各支路延迟不匹配的输出波形

以上两路无交叠边沿误码可推广到级无交叠编码支路的情况，对于相互独立的数据锁存与编码误码，总误码率为

与数据跳变沿近似对齐模式不同的是，数据跳变沿非对齐模式下各权重数据位变化的频率均对锁存误码有贡献，且延迟失配对误码的影响也比跳变沿近似对齐模式下的更大。对于Gary码编码方法，因各编码支路上升沿相对延迟相等，设为dr，下降沿相对延迟相等，设为df，则编码误码简化为

在各编码支路频率均相同的情况下，如同频码编码，式(7)可进一步简化为

因此，不同编码方式在不同状态条件下的误码率，可以通过以上解析模型定量描述。

4 低误码率设计

根据所建立的误码模型，首先分析降低误码的基本策略和方法，随后给出具体的实现方案并加以验证。

4.1 编码误码抑制分析

降低触发器建立保持时间和编码数据的频率，是降低锁存误码的基本方法。对于延迟失配造成的编码误码可以通过控制采样信号延迟以减小此类误码所占的比重。为简化分析，对每路数据信号的高低电平传输延迟采用对称近似，即dr1=df1=t1,dr2=df2=t2；但不同编码支路因逻辑门和路径深度不同，其传输延迟并不相同。设t1>t2，若控制采样信号同步延迟t2，等效为采样信号不变，将与同步左移t2，如图3中和虚线所示。

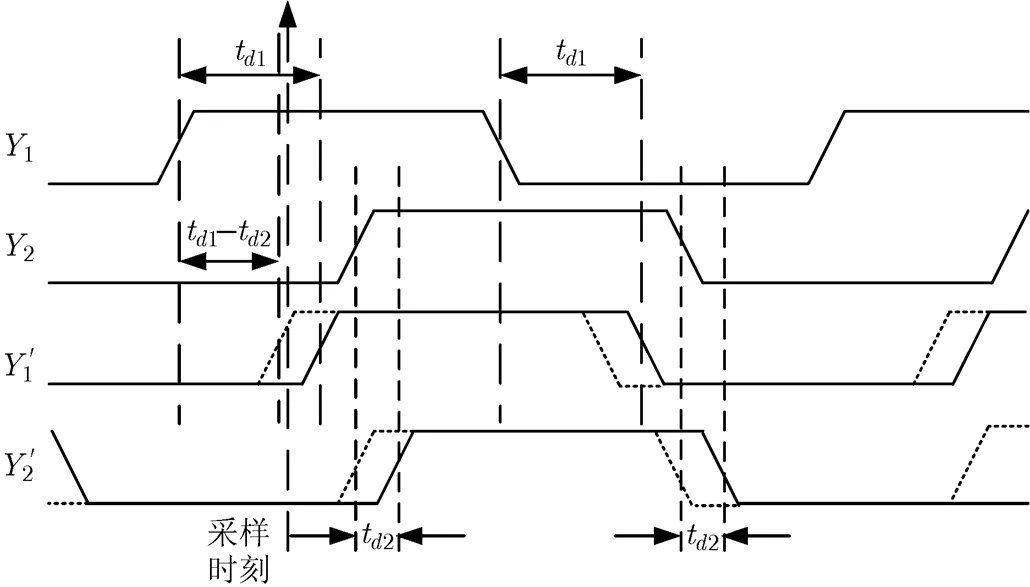
图3 采样信号延迟td2的等效波形

采样信号经过某种延迟匹配控制后的编码误码率与未经延迟匹配的编码误码率比值为

实际上，编码数据高低电平传输延迟并不相同，即dri¹dfi；并且采样信号传输延迟t与数据传输延迟相对独立，由此得到的路编码数据的编码误码率为

对于传输延迟不匹配边沿非交叠的两路编码，若t1=2t2，则=33.3%。随着t1与t2逐渐接近，且与采样信号延迟匹配，则编码误码率逐渐变小，当t1=t2=t时，=0且编码误码率2x=0，即延迟匹配的理想条件下可彻底抑制编码误码。实际设计编码电路时，要求条编码数据支路的延迟以及采样信号的延迟均尽可能匹配。

4.2 编码电路设计

本文暂不考虑数据锁存误码的抑制，编码电路设计仅考虑降低延迟失配引入的非理想编码误码。由于多相位时钟信号相位数多为2的幂次方，因此二进制编码最为常用。相状态节点编码后的状态位数=log2，当很大时，位数大幅度减小，致使传输输出的数据位数明显下降，因此编码有助于减小芯片面积和数据传输时间等开销。当时，编码不可省。以=16相输入、=4位输出的二进制编码电路为例，根据延迟链中16个结点状态的特定组合关系，判断检测采样信号在一个时钟周期内的相对位置，经编码得到4位数据输出1~4，其中1为最高权重位，4为最低权重位，具体逻辑关系及其对应的逻辑电路见表1(A)栏，其中B为延迟链中第级输出的节点状态，=1~16。

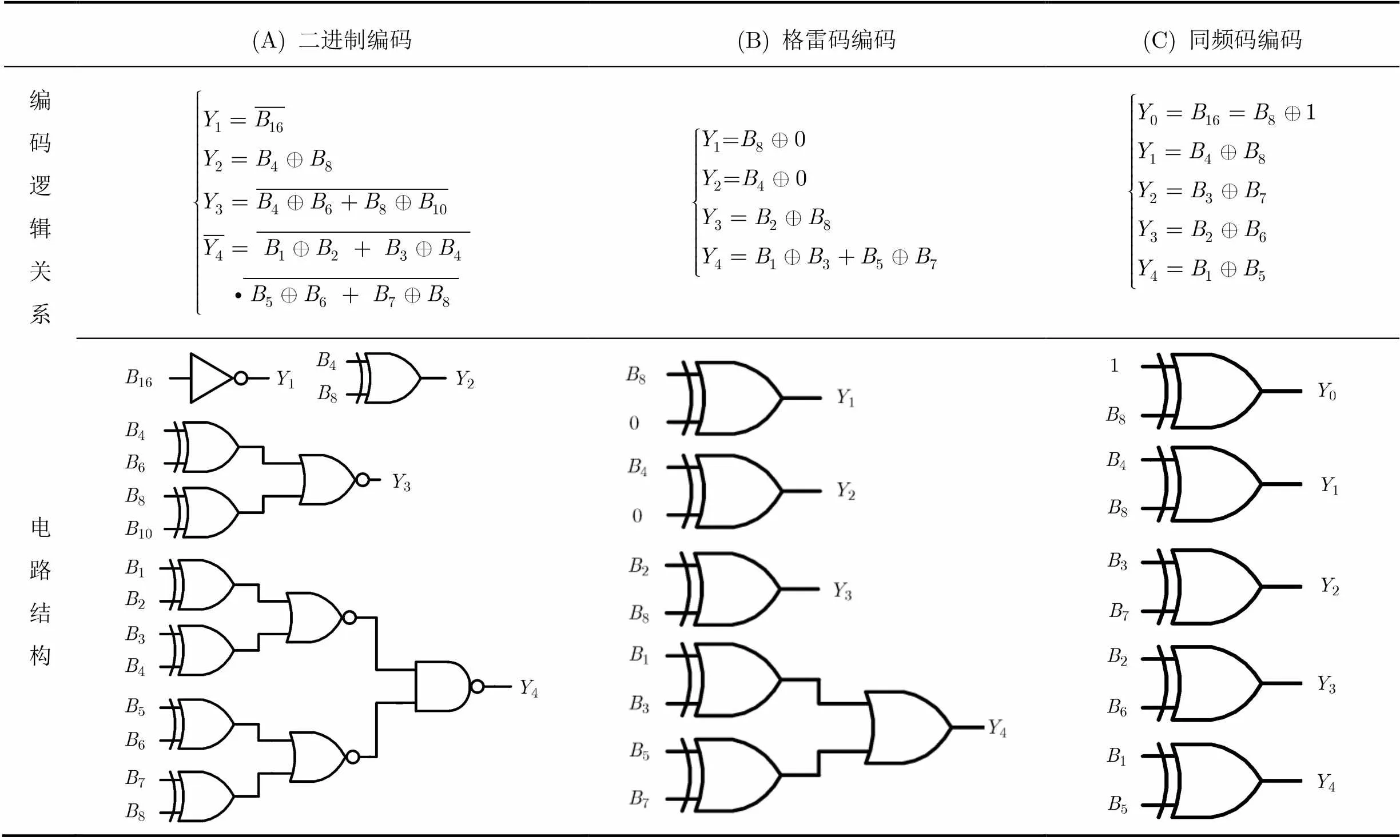
表1 3种编码逻辑关系及电路结构对比

门控信号有效的计数模式下，编码电路始终有效，即输出1~Y始终在循环变化并在采样信号到来后锁存。对于二进制编码方式，权重降低1位则频率翻倍，位编码输出，权重最低编码位输出数据Y的频率为权重最高位即结点信号时钟频率的倍。由二进制编码逻辑可以看出，4条编码支路的输入驱动和延迟传输路径各不相同，最低位4延迟最大且频率最高，误码率最高。由于编码各支路延迟均有失配，调节采样信号只能满足其中一路编码支路延迟匹配的要求，编码误码率难以降低。

采用格雷码编码可部分解决非理想编码误码问题[13]，格雷码作为一种无权单步自补码，具备反射特性和循环特性，同时具有消除随机取数时出现重大误差的能力[14]。格雷码在任意两个相邻数之间转换时，只有一个权重数位发生变化意味着无交叠沿，最大数与最小数之间也仅一个状态数不同，大大减少了状态转换过程中逻辑发生混淆的概率。编码前将16个状态分为单独的16等分，其最低位4有8个跳变沿，要使各位频率最低，1~4所有边沿相加应等于16，由于1和同频的2均对应2个边沿，2倍频的3对应4个边沿，以上各位相加恰好等于16。4位格雷码编码输出及对应的逻辑电路如表1(B)栏所示。同等条件下，最高权重位频率比对应的二进制编码降低一半，该支路的锁存误码率自然降低。但格雷码中各级延迟失配依然存在，编码误码仍无法完全消除。

假设编码后1~4依然保持16种原始状态，但重新调整其排列顺序，保证每位信号频率相同，为此需再增加一位0仲裁位，构成同频编码，一种同频编码逻辑关系如表1(C)栏所示，除0外，1~4每位输出异或逻辑的两位输入状态节点均间隔4个节点，因此输出频率相同，附加的0仲裁位频率相比以上节点频率减半。对比表1中的3种编码方法的电路结构，仅同频编码电路中5个编码输出支路同时可以实现比较严格的对称匹配，抑制编码误码的效果最佳。

5 仿真计算与测试结果分析

5.1 仿真评估

二进制、格雷码、同频码3类编码方式都存在触发器固有的锁存误码，在触发器建立保持时间固定不变的条件下，误码率与编码数据相对延迟及各编码位的频率有关。在相同的时钟频率驱动下，可根据各类编码不同位的频率，计算出各权重位的固有锁存误码率，再计算各支路延迟失配产生的编码误码，进而评估整体误码水平。

图4(a)为二进制编码输出波形，其中横坐标为仿真的时间，纵坐标为电压值，电压值的高、低分别代表逻辑电平1和0。图中各条支路边沿近似对齐且频率依次成倍数关系，若编码位相邻跳变区相互靠近距离小于建立保持时间，则需采用数据跳变沿近似对齐的误码模型，否则该两路编码应采用数

据跳变沿非对齐的误码模型。采样信号出现在各编码数据信号跳变沿附近的锁存误码可以利用式(3)或式(4)方便得到，在理想交叠条件下等效频率为各权重位中的最高频率；在非交叠模式下所有权重位均有效，等效频率取各权重位频率之和。

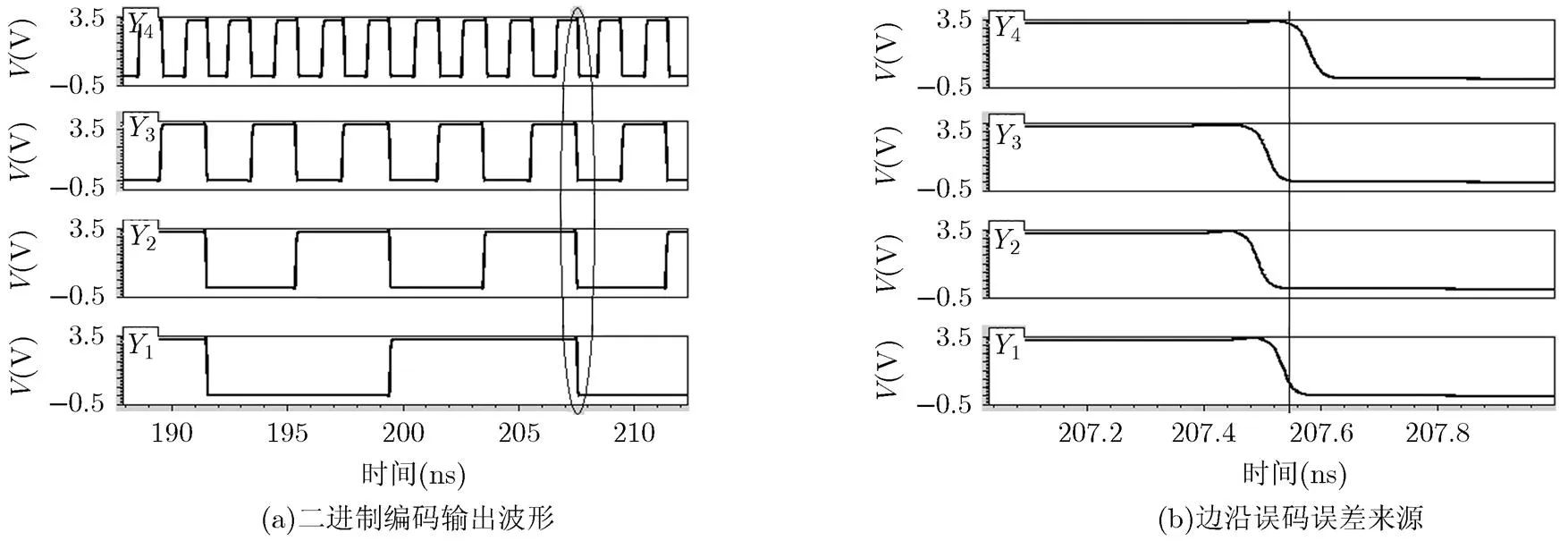
图4 二进制编码及其误码计算示意图

格雷码编码输出仿真结果如图5所示，各编码输出均无交叠沿，1与2保持原有编码输入频率不变，则其它两路数据的频率相比二进制编码方法同比特位频率减半，对应的锁存误码率同比例下降。4条传输链不匹配造成的边沿延迟偏差引入明显的编码误码。

图5 格雷码编码输出波形

同频编码输出仿真结果如图6所示，编码输出的0~4中，1~4数据频率相同，且无交叠沿，该频率为时钟频率即仲裁位0频率的两倍。从1~44条链的逻辑结构看，其扇入数量相同，逻辑结构相同，逻辑门级数相同，延迟相同，频率稳定，编码误码率极低。同频率码所获得的性能改善所付出的代价，是增加了一位冗余仲裁位0，仲裁位的应用使编码电路的面积略有增加。

图6 同频率码编码输出波形

电路中采用的主从式DFF触发器，其高电平建立、保持时间均为0，低电平建立、保持时间分别为70 ps, 100 ps，计数时钟频率0=40 MHz。3种编码方式的锁存误码率和编码误码率均可根据不同模式下的误码模型直接计算得到。假设二进制编码与其它两种编码方法一样均适用于边沿非对齐模型，则对于二进制、格雷码和同频码3种编码方式，每种编码模式下各权重位等效频率分别为0+20+ 40+80=150,0+0+20+40=80,0+20+20+20+ 20=90，即3种编码的锁存误码率比例关系近似为15:8:9。实际二进制编码因边沿近似对齐带来的相邻数据位建立保持时间的部分交叠，其近似交叠模式下误码计算结果相比以上非交叠模式有不同程度的降低。对3种编码电路分别进行各自条件下的最佳延迟匹配，理论计算结果如表2所示，结果表明，同频码在同等时钟频率下的误码率最低，其编码误码近似为0，与无编码的数据直接锁存电路总误码率等效；虽然增加了1个用于冗余位所需的触发器电路，但总误码率分别降低到二进制码的1/2和格雷码的3/5左右，且编码位最高频率的降低可带来明显的功耗降低。

表2 3种编码方式的误码率计算结果(%)

5.2 测试结果

一款基于双延迟锁定环的三段式TDC采用了低误码率的同频码编码方法，基于TSMCCMOS工艺流片。对TDC电路进行单射精度测量[15,16]，测试时选用4个不同档位进行精测，每一档位进行多组数据量测量，保证数据覆盖档位中较多时刻，针对300 ns档由100组扩大为500组。所有档数据按统计学原理进行粗处理，且数据服从高斯分布，取置信水平为0.95，默认区间外数据为错误数据，即所默认误码造成的粗大误差结果。

表3给出了误码率测试分析的理论数据和实际测量数据，其中理论误码率即总误码率为触发器锁存误码率与编码误码率之和，将测量的错误数据组占测量组总数的比重，定义为实测的综合误码率。考虑到理论模型建模条件的近似和实际测试存在的误差，理论计算和实测结果近似吻合，两者之间的偏差在允许的范围内。对于同频编码电路，此时固有误码率占据主导，继续降低误码率，将主要依靠降低工作频率、减小触发器建立保持时间所带来的本征锁存误码率的降低。

表3 误码率测试分析(%)

档位(ns)测试组数无效组数误码率理论误码率综合误码率 50100 666.15.13 200100 44 300500254 500100 64

6 结束语

基于数据采样和编码的误码机制，本文提出了典型工作条件和状态模式下的误码模型，分析了误码产生根源并提出降低误码率的实现方法，即降低编码位最高频率并减小各编码支路的延迟失配。对优化后的编码电路完成了基于TSMCCMOS工艺流片和测试验证，误码率的实测结果与理论计算相吻合，验证了误码模型的正确性和误码抑制方法的有效性。

[1] LI Qianfeng and HU Qingsheng. A 10ps 500MS/s two-channel Vernier TDC in 0.18CMOS technology[C]. IEEE Workshop on Advanced Research and Technology in Industry Applications (WARTIA), Ottawa, Canada, 2014: 1268-1271. doi: 10.1109/WARTIA.2014.6976513.

[2] BREZINA C, FU Y, ZAPPON F,. GOSSIPO-4: evaluation of a Novel PLL-based TDC-technique for the readout of gridpix-detectors[J].2014, 61(2): 1007-1014. doi: 10.1109/ TNS.2014.2301141.

[3] UCHIDA Daisuke, IKEBE Masayuki, MOTOHISA Junichi,. A 12-bit, 5.5-μW single-slope ADC using intermittent working TDC with multi-phase clock signals[C]. International Conference on Electronics, Circuits and Systems (ICECS), Marseille, France, 2014: 770-773. doi: 10.1109/ICECS. 2014.7050099.

[4] KALISZ J, SZPLET R, PELKA R,. Single-chip interpolating time counter with 200-ps resolution and 43-s range[J]., 1997, 46(4): 851-856. doi: 10.1109/19.650787.

[5] KATOH Kentaroh, DOI Yoshihito, ITO Satoshi,. An analysis of stochastic self-calibration of TDC using two ring oscillators[C]. IEEE Conference on Asian Test Symposium (ATS), Jiaosi Township, China, 2013: 140-146. doi: 10.1109/ ATS.2013.35.

[6] URANO Yuki, YUN WonJoo J, KURODA Tadahiro,. A 1.26 mW/Gbps 8 locking cycles versatile all-digital CDR with TDC combined DLL[C]. International Symposium on Circuits and Systems (ISCAS), Beijing, China, 2013: 1576-1579. doi: 10.1109/ISCAS.2013.6572161.

[7] 姚茂群, 张立彬, 耿亮. 电流型 CMOS 脉冲 D 触发器设计[J]. 电子与信息学报, 2014, 36(9): 2278-2282. doi: 10.3724/ SP.J.1146.2013.00343.

YAO Maoqun, ZHAGN Libin, and GENG Liang. Design of current-mode CMOS pulse-triggered D flip-flops[J].&, 2014, 36(9): 2278- 2282. doi: 10.3724/SP.J.1146.2013.00343.

[8] 欧庆于, 罗芳, 吴晓平. 基于 NCL 电路的抗故障攻击设计研究[J]. 电子与信息学报, 2014, 36(7): 1648-1655. doi: 10.3724/ SP.J.1146.2013.00750.

OU Qingyu, LUO Fang, and WU Xiaoping. The research on countermeasure against fault attacks for NCL circuits[J].&, 2014, 36(7): 1648-1655. doi: 10.3724/SP.J.1146.2013.00750.

[9] PELKA R, KALISZ J, and SZPLET R. Nonlinearity correction of the integrated time-to-digital converter with direct coding[J]., 1997, 46(2): 449-453. doi: 10.1109/19.571882.

[10] POLAT Ö and MANZAK A. Design and analysis of low power Carbon Nanotube Field Effect Transistor (CNFET) D Flip-Flops (DFFs)[C]. International Conference on Computer Research and Development (ICCRD), Shanghai, China, 2011, 3: 399-401. doi: 10.1109/ICCRD.2011.5764223.

[11] TAIT A N and PRUCNAL P R. Applications of wavelength-fan-in for high-performance distributed processing systems[C]. Proceedings of the IEEE/ACM International Symposium on Nanoscale Architectures, Paris, France, 2014: 177-178. doi: 10.1109/NANOARCH.2014. 6880485.

[12] JIN Wei, LU Sheng, HE Weifeng,. Robust design of sub-threshold flip-flop cells for wireless sensor network[C]. International Conference on VLSI and System-on-Chip (VLSI-SoC), Hong Kong, China, 2011: 440-443. doi: 10.1109/VLSISoC.2011.6081623.

[13] SALIGRAM Rakshith and RAKSHITH T R. Contemplation of synchronous Gray Code counter and its variants using reversible logic gates[C]. IEEE Conference on Information & Communication Technologies (ICT), JeJu Island, Korea, 2013: 661-665. doi: 10.1109/CICT.2013.6558177.

[14] KALISZ J, PAWLOWSKI M, and PELKA R. Error analysis and design of the Nutt time-interval digitiser with picosecond resolution[J].:, 1987, 20(11): 1330-1341.

[15] REDANT Tom, STUBBE Frederic, and DEHAENE Wim. A low power time-of-arrival ranging front end based on a 8-channel 2.2 mW, 53ps single-shot-precision time-to-digital converter[C]. IEEE Conference on Solid State Circuits, Jeju, Korea, 2011: 321-324. doi: 10.1109/ASSCC.2011.6123578.

[16] HENZLER Stephan. Time-to-Digital Converters[M]. London, Springer Science & Business Media, 2010: 25-31.

Research on Low Bit Error Rate Encoding Method for Data Latch Processing

WU Jin①JIANG Qi②ZHENG Lixia①SUN Dongchen②SONG Ke②SUN Weifeng②

①(,,214135,),②(,,210096,)

In the data processing of quantified time signal, traditional encoding method in high frequency is faced with the problem of high Bit Error Rate (BER) affecting the data’s quantitative accuracy. This paper presents BER mechanism analytical model according to the analysis of the causes of bit error, which takes both data latch and delay mismatch effects of different state pattern into consideration. And the analysis of same frequency coding mode with low BER is put forward based on the comparison of the binary and Gray coding method. The circuit and layout designs of Time to Digital Converter (TDC) with same frequency coding mode are implemented in TSMC 0.35mm CMOS process. The test results of the Multi Project Wafer (MPW) chip show that BER of the same frequency coding mode is effectively reduced compared with traditional encoding modes under the same conditions.

Coding circuit; Time to Digital Converter (TDC); Bit Error Rate (BER); Data sampling

TN402

A

1009-5896(2016)07-1831-07

10.11999/JEIT151104

2015-09-29；改回日期：2016-03-03；网络出版：2016-04-07

郑丽霞 zhenglx79@163.com

江苏省自然科学基金(BK2012559)

Natural Science Foundation of Jiangsu Province (BK2012559)

吴 金： 男， 1965年生，博士，教授，研究方向为集成电路设计、红外传感信号检测.

江 琦： 男， 1992年生，硕士生，研究方向为时间数字转换电路设计.

郑丽霞： 女， 1979年生，讲师，研究方向为红外读出电路.