触发器逻辑功能转换的两种方法

陈海霞，丛云飞

(通化师范学院 物理系，通化 吉林 134002)

触发器是具有记忆功能的基本逻辑单元，一个触发器能够存储1位二进制信息．它是时序数字电路的最基本的单元，每个时序电路都少不了触发器．随着科学的进步，社会的发展，时序电路在很多领域中得到了广泛的应用．

1 触发器的概述

1.1 触发器的相关概念

触发器是个特殊的存储过程，它的执行不是由程序调用，也不是手工启动，而是由事件来触发．触发器具有两个能自行保持的稳定状态，用来表示逻辑状态的0和1，或二进制数的0和1．在外界信号作用下，输出信号可以从一个稳态转变为另一个稳态，无外界信号作用时，输出状态保持不变．因此，触发器是一种具有记忆功能的二进制存贮器件，是构成各种时序电路的基本逻辑单元，它在数字系统和计算机中有着广泛的运用．

逻辑功能是指触发器的次态和现态及输入信号之间在稳态下的逻辑关系.这种逻辑关系可以用特性表(功能表)、特性方程或状态转换图等给出.

电路结构是指电路中门电路的种类及组合方式. 基本RS触发器、同步RS触发器、主从触发器、边缘触发器等是电路结构的不同形式.由于电路结构形式的不同，带来了不相同的动作特点. 同一种逻辑功能的触发器可以用不同的电路结构实现.反过来说，用同一种电路结构形式可以作成不同逻辑功能的触发器.

1.2 触发器的分类

逻辑功能的描述方法：逻辑符号、特性表、驱动表、特性方程.

按照逻辑功能的不同，可分为RS触发器、JK触发器、D触发器和T触发器等．

按触发方式不同分为：电平触发器、边沿触发器和主从触发器．

按电路结构不同分为：基本RS触发器、同步SR触发器、主从触发器、维持阻塞触发器、边沿触发器、钟控触发器等．

按存储数据原理不同分为：静态触发器和动态触发器，静态触发器是靠电路的自锁来存储数据的，动态触发器是靠电容存储电荷来存储数据的．

按构成触发器的基本器件不同分为：双极型触发器和MOS型触发器．

2 转换的两种方法

在现有集成触发器的产品中，每一种触发器都有着自己固定的逻辑功能．当今的市场提供的集成触发器型号也是比较多的，目前生产的触发器定型产品中以JK触发器和D触发器这两大类为主，但是在实际应用中经常需要用到的是其它功能的触发器．为了达到这些要求，可以在已有的触发器的基础上，给它们附加逻辑电路，利用逻辑功能转换的方法获得所需功能的触发器．

图1就是常用触发器功能转换的结构示意图，由图知道触发器的转换关键是怎样设计附加组合逻辑电路，即转换电路．进行设计附加组合逻辑电路的要求有：转换前的触发器(已有触发器)和转换后的触发器(待求触发器)特性方程相同．目前常用的有代数法和图表法两种转换方法．这两种方法也是逻辑函数化简的两种最常用的方法，用化简后的表达式构成逻辑电路可节省器件，降低成本，提高工作的可靠性．

图1 触发器逻辑功能转换示意图

2.1 代数法

代数法是不同触发器进行转换最简单和最直接的方法，就是利用基本逻辑公式把待求触发器的特性方程转换成我们已有触发器的特性方程的形式，然后比较已有和待求触发器的特性方程，直接推导出已有触发器的输入端与待求触发器的输入端及状态之间的逻辑关系，从而得到所需的附加组合电路的输入和输出表达式，即转换关系的逻辑表达式．

代数化简法是根据逻辑代数的基本定律(交换律、结合律、分配律、互补律、反演律)，利用并项法、吸收法、消去法、配项法，将逻辑式化为最简式．

转换方法：利用令已有触发器和待求触发器的特性方程相等的原则，求出转换逻辑．

转换步骤：首先，写出已有触发器和待求触发器的特性方程，变换待求触发器的特性方程，使之形式与已有触发器的特性方程一致．然后，比较已有和待求触发器的特性方程，根据两个方程相等的原则求出转换逻辑．最后，根据转换逻辑画出逻辑电路图．

例1 用RS触发器转换构成JK触发器．

解：首先变换JK触发器特性方程，使之与RS触发器特性方程的形式一致．

再对照比较以上两类触发器的特性方程，可得转换关系逻辑表达式:

图2 RS触发器转JK触发器逻辑图

2.2 图表法

图表法是另一种应用于触发器之间逻辑转换的重要方法，图表法的依据是描述触发器功能的真值表与激励表，关键就是卡诺图的利用．图表法的过程是先列出要实现的目标触发器的功能真值表，该真值表反映的是在不同的输入组合及不同的状态下，目标触发器次态的值，再根据我们已有的触发器的激励表，在上述真值表中列出每一行不同状态的转换对应已有触发器输入端的值，最后以此表为依据推导出已有触发器的输入端与待求触发器的输入端及状态之间的逻辑关系．然后利用卡诺图求出转换关系的逻辑表达式，最后根据逻辑表达式画出逻辑图．

卡诺图是一种平面方格图，每个小方格代表一个最小项，故又称为最小项方格图.卡诺图在构造上具有以下两个特点：n个变量的卡诺图由2n个小方格组成，每个小方格代表一个最小项和卡诺图上处在几何相邻的小方格所代表的最小项为相邻最小项．

卡诺图法化简的基本步骤：首先，将逻辑函数化成与-或式；其次，绘卡诺图和根据逻辑函数项填卡诺图；再次，圈卡诺圈：卡诺圈包围方格数必须满足2n的规律(n∈R)，并要尽可能大．每个方格都应被卡诺圈包含，每个卡诺圈至少含有一个新方格；最后，得出逻辑函数化简后的最简与-或式．

例2 将RS触发器转换成JK触发器．

解：JK触发器特性表如表1所示：

表1 JK触发器特性表

RS触发器激励表如表2所示：

表2 RS触发器激励表

表3 RS转JK关系真值表

我们知道RS触发器转换成JK触发器必须要求两类触发器具有相同的状态．

例如，对于JK触发器，当J=K=0时，保持状态即Qn=Qn+1．对于RS触发器，当Qn=Qn+1=0时，状态保持不变或状态置0．由JK触发器特性表和RS触发器激励表可以得到RS触发器转换JK触发器关系真值表，如表3．

由表3我们可以作出输出函数的卡诺图如图3.

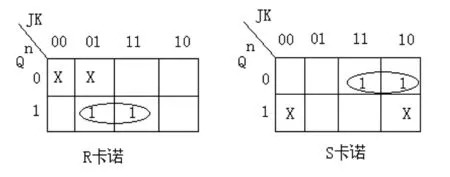
图3 输出函数卡诺图

通过卡诺图的简化可以得到转换逻辑关系的逻辑表达式：

故可得到RS触发器转JK触发器逻辑图，如图4．

图4 RS触发器转JK触发器逻辑图

3 结语

通过上面的述说，可以知道代数法和图表法对于处理触发器逻辑功能转换问题是比较方便．在触发器逻辑功能转换问题转换的过程中，可以根据实际情况选择代数法和图表法，如果对触发器的特性方程掌握较好，并对逻辑函数代数化简的方法掌握较好的情况下，可以选用代数法；如果对触发器的特性方程不十分掌握而对转换激励表比较掌握，并对逻辑函数卡诺图化简掌握较好的情况下，可以选用图表法．这两种方法最终达到的目的是一致的，转换过程有各自的特点，若能合理选择，定能将转换做得又快又准确．

参考文献：

[1]梁明理.电子线路[M].北京：高等教育出版社,2008．

[2]陈其纯．电子线路[M].北京：高等教育出版社,2001．

[3]蔡良伟.数字电路与逻辑设计[M].西安：西安电子科技大学出版社,2003．

[4]李大友.数字电路逻辑设计[M].北京：清华大学出版社,1997．