卓越师资班线性代数课程矩阵乘法教学方法研究

马中华



卓越师资班线性代数课程矩阵乘法教学方法研究

马中华

（天津职业技术师范大学 理学院，天津 300222）

结合卓越师资班的培养要求，探讨线性代数课程矩阵乘法算法的结构分析教学方法．通过逐层分析探寻矩阵乘法的规则和实际意义，突出教学重点，突破教学难点，旨在开阔学生对矩阵乘法原理的理解，并为解决实际工科问题提供思路．

线性代数；矩阵乘法；卓越师资班

近年来，职业教育教师培养在国家政策支持下不断地完善，职业教育教师培养质量得到显著提高，但也存在着职业教育教师培养的适应性和针对性不强，部分课程教学内容和教学方法与应用型教师人才培养结合度不高等突出问题．如何在“十三五”发展期间持续提高职业教育教师培养质量，成为我国教师教育改革发展最核心、最紧迫的任务之一．

卓越职教师资培养实验班（简称卓越师资班）是以培养专业基础扎实、职业技能水平高、综合施教能力强的职业院校专业教师为目标，采用个性化的职业教育培养方案和独特的卓越师资管理方式，选拔具有职业教育教师潜质，乐于从教，适合从教的大学本科学生．卓越师资班实施单班教学，要求教学方式和教学方法更加丰富新颖，尤其注重师范技能与专业相结合的全方位实践教学．对卓越师资班的日常教学，尤其是基础数学课程教学，要打开学生思路，化抽象的概念和公式为形象的算法和流程，摆脱死记硬背．

在工科数学中，为了解决工程实际问题，线性代数课程要面向矩阵和向量应用，根据非数学专业学生的水平和需要组织课程内容，并为一些后续课程的学习及在各个学科领域中进行理论研究和实践工作提供必要的保证[1]．矩阵理论是线性代数的核心内容之一，矩阵理论的学习是学生学好线性代数的关键[2-3]．矩阵乘法是矩阵理论的重要组成部分，但由于矩阵乘法的内涵具有较高的抽象性和多样性，造成学生在理解时的困难[4]．通用教材中直接给出矩阵乘法计算公式，难免显得突兀，同时学生也会疑惑，为何矩阵乘法公式不是对应矩阵元素的乘积的结果．为了加深学生对这一抽象算法的理解，在卓越师资班教学中尝试应用了解析算法的结构分析教学法，学生普遍反应良好．

1代数几何意义的解释

国内外工科线性代数课程安排顺序不尽相同，本课程借鉴国外优秀教材[5]，在线性代数矩阵理论教学过程中插入具有代数几何意义的解释．

首先，通过数形结合的方式给学生建立线性映射和线性变换等基本概念．其次，矩阵的定义[6]中指出行（列）矩阵又称行（列）向量．因此，在讲授矩阵计算之前，需向学生简单说明什么是向量，所有向量所构成的集合表示为．向量是对矩阵的特殊解释，向量与矩阵的运算规则一致．最后，将线性映射与线性方程组建立联系．从到的线性变换也可以称为线性映射，从2×1向量到3×1向量的线性映射可用一次线性方程组的形式来表示，即

式（1）所对应的向量方程可写成

然而，线性方程组及向量方程的表达方式不利于学生从视觉效果联想二维空间向量变换到三维空间向量的过程．若从几何意义出发，则很容易理解向量经过一次线性映射后的结果是不同领域或空间的向量，而矩阵即是映射（见图１）．图1中，空间中的向量经线性映射成为空间中的向量．

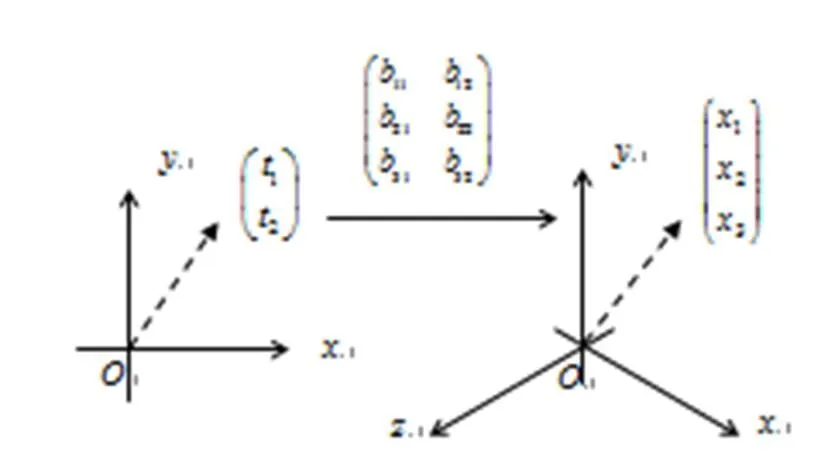
图1　线性空间中的向量及矩阵对应的映射

2矩阵乘法算法的结构分析

2.1基于矩阵和向量乘法的结构分析法

学生在学习新知识时，往往会以旧知识作为基础，但新知识又有自己的特点．以线性方程组为中心讲述矩阵乘法运算原理和方法，通过图表展示矩阵乘法运算内部的结构[7]，学生会更有兴趣，也能够更深刻地理解运算规则的来龙去脉，分清概念，顺利地完成新知识的学习，起到事半功倍的效果．

通过由一次线性方程组出发的线性映射结构（见图２）及代数几何意义的解释，学生可观察得到如下信息：

（1）矩阵与向量的乘积结果是向量．

（2）矩阵列数为输入的向量维数，矩阵行数为输出的向量维数．

（3）向量行数为输入的向量维数，向量列数为输出向量数．

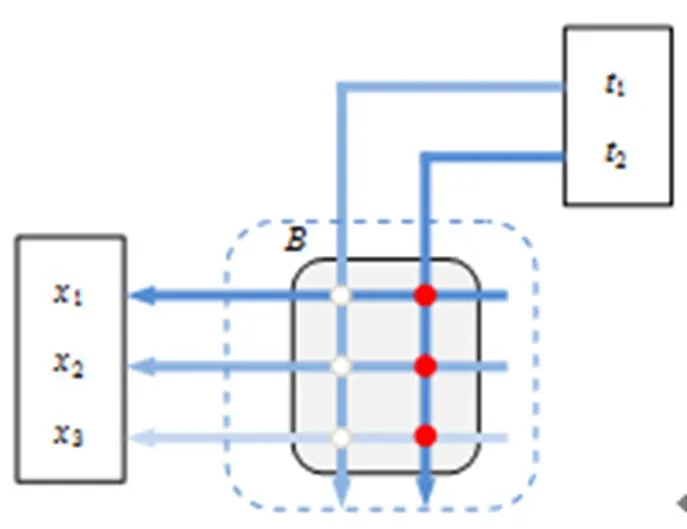
图2　线性映射结构示意图

（3）将结果列向量组合．

图3　线性映射的合成结构示意图

图4　矩阵乘积

2.2基于向量和向量乘法的结构分析法

（2）将这2个输出向量做向量加法运算得到完整输出向量，即

（2）将这3个输出矩阵做矩阵加法运算得到完整输出矩阵，即

综上，在讲授矩阵乘法运算结构的基础上，学生自然会理解矩阵乘法运算中，为何不可随意交换矩阵乘法顺序，不可随意消去非零矩阵，但是矩阵乘法的结合律和分配律等运算规则仍可保留沿用．

3结束语

线性代数课程是大学基础教学的重要组成部分，特别是对于理工科专业的学生．从实际应用层面上来看，线性代数课程为非数学专业学生后续课程的学习、研究和实践工作提供了必要的理论基础．针对卓越师资班教学注重基础、开阔思路、培养思考方法的要求，本文从矩阵与向量乘法的结构出发，给出具有较好物理和空间意义的矩阵乘法计算方法．

将学习回归为应用，是优化卓越师资班人才培养机制的目标之一．希望通过一系列的教学方法改革，从细节处提升学生将实际工程问题转化为代数问题的能力，激发学生进一步深入研究的兴趣．

[1] 陈怀琛．线性代数要与科学计算结成好伙伴[J]．大学数学，2010（S1）：28-34

[2] 袁可红，李艳晓．分形思想在线性代数教学中的应用[J]．高师理科学刊，2012，32（5）：97-99

[3] 王颖．将解析几何融入线性代数教学中的思考[J]．高师理科学刊，2013，33（4）：62-64

[4] 林海波．比较法和反例在矩阵乘法教学中的应用[J]．中国科技信息，2011（17）：180

[5] Lay D C，Lay S R，McDonald J．Linear Algebra and Its Applications[M]．5th ed．New York：Pearson，2015

[6] 同济大学数学系．线性代数[M]．6版．北京：高等教育出版社，2014

[7] 平冈和幸，堀玄．程序员的数学3：线性代数[M]．卢晓南，译．北京：人民邮电出版社，2016

[8] Strang G．Linear Algebra and Its Applications[M]．4th ed．Belmont：Brooks/Cole/Cengage，2006

Study on teaching method of matrix multiplication in the linear algebra course of excellent teacher class

MA Zhong-hua

（School of Science，Tianjin University of Technology and Education，Tianjin 300222，China）

Combined with the teaching requirements of excellent teacher class，mainly discusses the structure of the matrix multiplication algorithm of linear algebra course．In order to highlight the teaching focus，to break through the teaching difficulties，analyze the rule and the practical significance of matrix multiplication．The aim is to develop students′ understanding of the principle of matrix multiplication，and to provide ideas for solving practical engineering problems.

linear algebra；matrix multiplication；excellent teacher class

1007-9831（2016）07-0066-04

O151.2∶G642.0

A

10.3969/j.issn.1007-9831.2016.07.018

2016-05-18

马中华（1983-），男，黑龙江克山人，讲师，博士，从事高性能计算研究．E-mail：mazhonghua1983@aliyun.com