常微分方程线性系统的一般理论与方程求解

马军，李长江



常微分方程线性系统的一般理论与方程求解

马军，李长江

（河北民族师范学院 数学与计算机科学学院，河北 承德 067000）

在常微分方程的全部内容中，线性系统部分占有特别重要的地位，这不仅因为其自身的理论已被研究得十分清楚外，同时线性系统又是讨论非线性系统的基础．利用线性空间理论进一步对常微分方程线性内容及方程求解做一些分析和探究．

常微分方程；线性系统理论；常系数线性方程；求解

常微分方程是数学与应用数学专业的一门主要基础课程，线性方程理论是该门课程的主要内容．如果能把线性方程理论放到高等代数线性空间框架下去理解，那么线性微分方程理论实质上是线性空间理论的一个具体应用，这样可以帮助学生更好地掌握线性方程与方程组通解结构的内涵，加深对不同分支数学理论统一性的认识.

1高阶线性微分方程与方程组的通解结构

设高阶线性微分方程

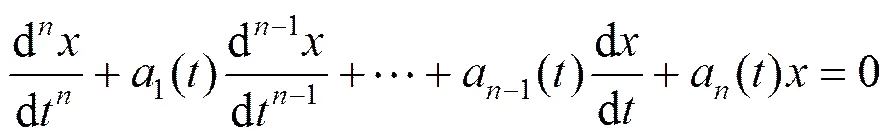
综合所述，得到以下结论：

利用这一结论判断方程（2）解函数的线性相关性非常方便，这种局部概括整体的思想在分析学中非常重要，必须熟练掌握．

关于线性微分方程组的通解结构问题，完全可以仿照上述思路，也就是引入函数矩阵和函数列向量后，若把函数向量当做通常的函数看待，则线性方程组的结论与线性方程的结论完全类似．即齐次线性微分方程组的全部解构成一个维向量空间，其通解是基本解组的线性组合；非齐次线性微分方程组的通解等于对应齐次方程组的通解和它的一个特解的和，这个特解可以由对应齐次方程组的通解用常数变易法求得.具体过程中同样引入了函数列向量的线性相关、线性无关、Wtonsky行列式等概念并作出相应类似的讨论.

需要说明的是：（1）无论是线性微分方程还是线性微分方程组，都可以不考虑通解．通解这个古典概念对于线性系统的理论并没有具体实际意义，既然已经求得了线性微分方程或方程组的全部解，就没必要纠缠通解问题，也省略了验证繁杂的雅柯比行列式[2]．（2）常微分方程线性系统理论是数学理论中较为完整的理论，搞清线性方程及方程组解的结构是对线性空间理论的一个很好复习与应用．另外，教科书中的一些证明显得过于繁琐，利用高等代数相关知识[3]完全可以适当简化，从而可以进一步弄清事物的本质．

2常系数线性微分方程及方程组的求解

常系数线性微分方程的求解问题从理论上说已经得到根本解决，尤其是求齐次线性微分方程可以不需要积分，具体的方法为Euler待定指函数法．常系数线性方程的一般形式为

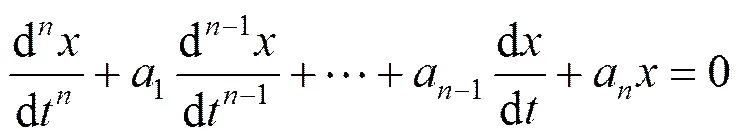
3线性微分方程与方程组的联系

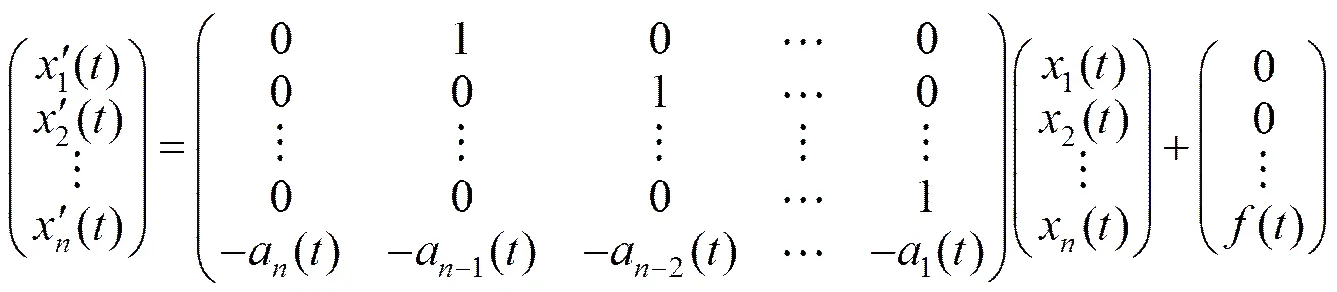
[1] 王高雄，周之铭．常微分方程[M]．3版．北京：高等教育出版社，2006：120-210

[2] 李长江．线性微分方程学法浅议[J]．高等函授学报：自然科学版，2006（5）：42-51

[3] 张禾瑞，郝鈵新．高等代数[M]．5版．北京：高等教育出版社，2007：211-256

[4] 石瑞青，严晓红，齐霄霏，等．微分方程全程导学及习题全解[M]．北京：中国时代经济出版社，2007：181-185

[5] 赵慈庚，朱鼎勋．大学数学自学指南[M]．北京：中国青年出版社，1984：71-79

[6] 丁崇文．常微分方程[M]．2版．厦门：厦门大学出版社，2006

The general theory of ordinary differential equation and solving equatio

MA Jun，LI Chang-jiang

（School of Mathematics and Computer Science，Hebei Normal University for Nationalities，Chengde 067000，China）

In all content of the ordinary differential equation，the part of linear system occupies an important position. It is not only because the theory itself has been researched clearly，but also linear system is the basis of nolinear system．Takes advantage of the linear space theory to analysis and research the ordinary differential equation and solving equation further.

ordinary differential equation；linear system theory；constant coefficient linear differential equation；solution

1007-9831（2016）07-0058-03

O175.1

A

10.3969/j.issn.1007-9831.2016.07.015

2016-04-06

马军（1964-），男，河北平泉人，副教授，硕士，从事常微分方程研究．E-mail：cdsz_lcj2006@sina.com