圆锥曲线特征点和线的若干性质

玉炳图

（广南县第一中学，云南 广南 663399）

圆锥曲线特征点和线的若干性质

玉炳图

（广南县第一中学，云南 广南 663399）

圆锥曲线焦点、顶点、准线和类准线是圆锥曲线的主要特征点和主要特征线，根据它们之间的关系，应用线到线的角公式，推导出一组重要的有趣的不等式，为解决相关问题提供解借鉴。

焦点；顶点；准线；离心率

由假设y>0及上式知tanθ>0，所以θ为锐角，由基本不等式得

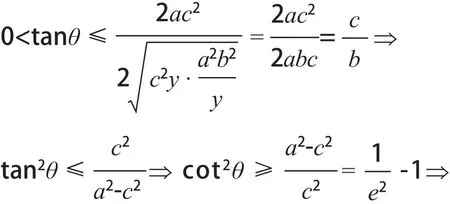
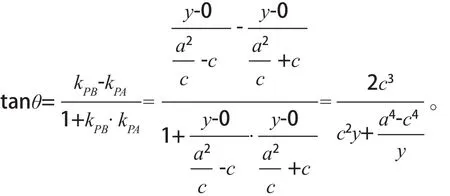
由假设y>0及上式知tanθ>0，所以θ为锐角，由基本不等式得

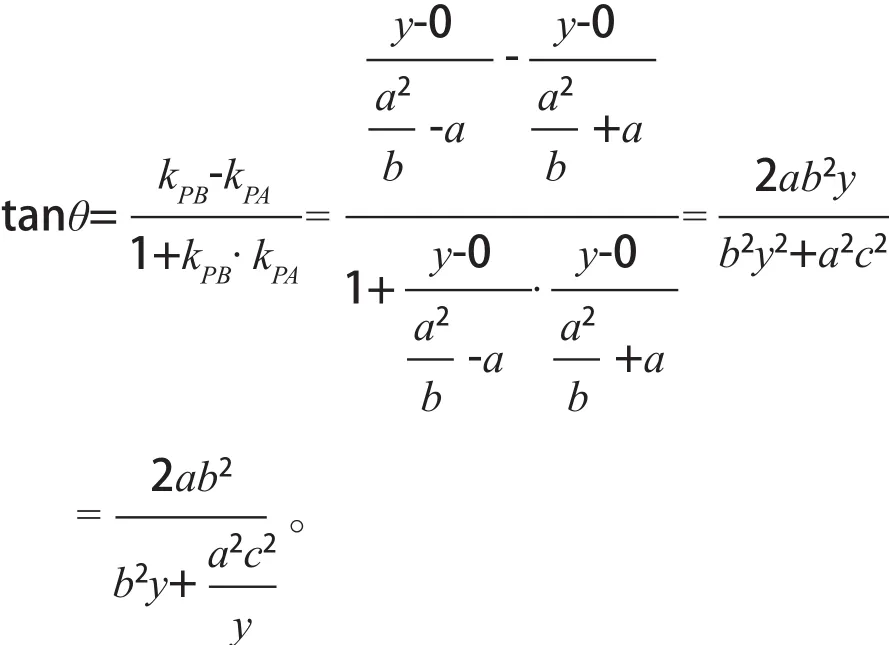
由假设y>0及上式知tanθ>0所以θ为锐角，由基本不等式得

以下同定理1的证明。

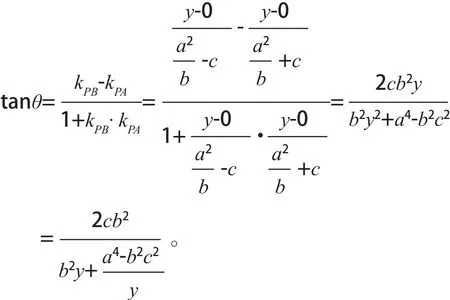
由假设y>0及上式知tanθ>0所以θ为锐角，由基本不等式得

由假设y>0，c>b及上式知tanθ>0所以θ为锐角，由基本不等式得

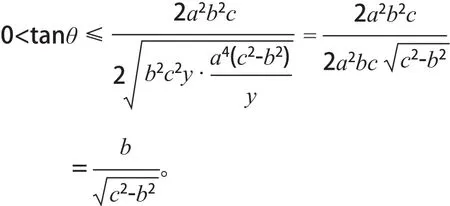
三个几何量a，b，c中，对于椭圆，a最大，对于双曲线，c最大，从而由椭圆的特征线联想到双曲线的特征线进行研究，则得：

由假设y>0及上式知tanθ>0所以θ为锐角，由基本不等式得

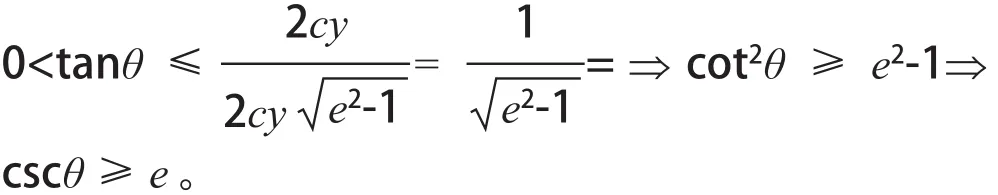
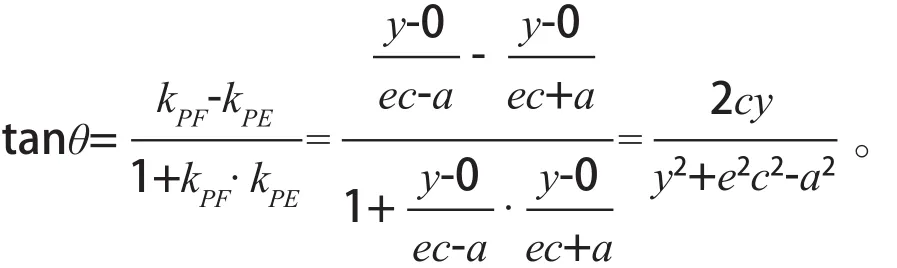
由假设y>0及上式知tanθ>0所以θ为锐角，由基本不等式得

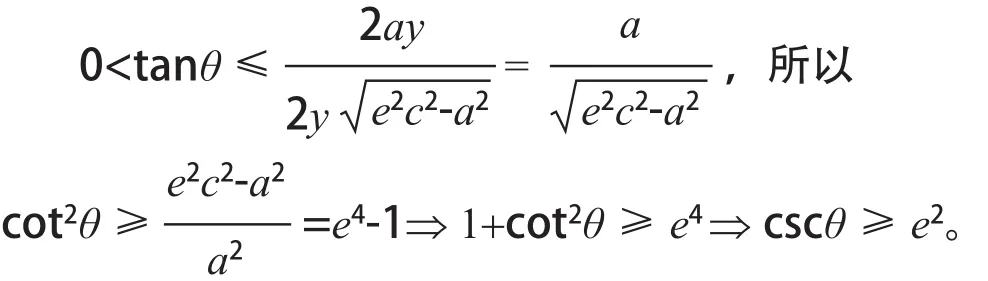
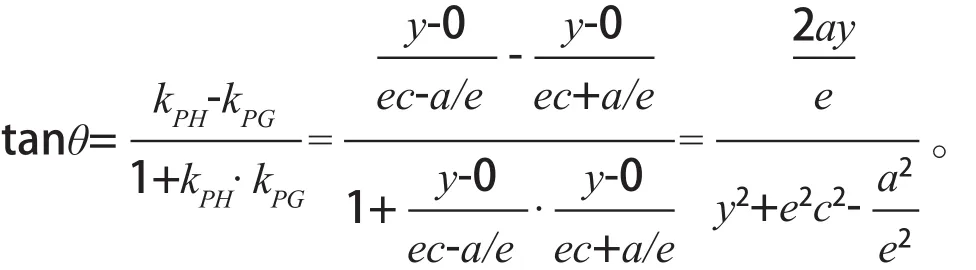
由假设y>0及上式知tanθ>0所以θ为锐角，由基本不等式得

由假设y>0及上式知tanθ>0所以θ为锐角，由基本不等式得

由假设y>0及上式知tanθ>0所以θ为锐角，由基本不等式得

则得

由假设y>0及上式知tanθ>0所以θ为锐角，由基本不等式得

如果联想到统一的圆锥曲线，进行研究，则得：

定理12P是圆锥曲线准线l上的动点，F，A是和l相应的焦点和顶点，e是离心率，P是焦点到相应准线的距离，准线l与对称轴的交点为H，FPA=θ，则θ为锐角且（当且仅当点时取等号）。

证明不妨以有向直线HAF所在直线为x轴，F为坐标原点建立直角坐标系，则得F(0, 0)，设M(x,y)是圆锥曲线上的一点，M到准线l∶x=-p的距离为d，则由圆锥曲线定义知|MF|=ep由此可得圆锥曲线为令y=0，并注意到xA<0解得点不妨设P (-P, y)在x轴上方，即y>0，则由线到线的角公式得

由假设y>0知tanθ>0所以θ为锐角，由基本不等式得

Some Properties of Feature Points and Lines of Conic Curve

YU Bingtu
(No.1 Middle School, Guangnan Yunnan 663399, China)

Focus, vertex, directrix and eccentricity are major feature points and lines of conic curve. The paper deduces a set of important and interesting inequalities based on their relations and using angle formula from line to line, which provides reference for solving concerning problems.

focus; vertex; directrix; eccentricity

O123.2

A

1674 - 9200（2016）03 - 0045 - 06

（责任编辑刘常福）

2015 - 05 - 27

玉炳图，男，云南广南人，云南省特级教师，全国模范教师，云南省委联系专家，主要从事高中数学教学和解析几何研究。