微带线FDM特性传输特性分析
刘秉安,刘青
(1.陕西工业职业技术学院陕西咸阳712000;2.陕西国际商贸学院陕西咸阳712000)
微带线FDM特性传输特性分析
刘秉安1,刘青2
(1.陕西工业职业技术学院陕西咸阳712000;2.陕西国际商贸学院陕西咸阳712000)
为了探讨微带线FDM特性传输特性,将Matlab应用于有限差分法的正演计算中,充分发挥了其强大而方便的功能。通过对二维稳定电流场模型的试算表明,Matlab在研究微带线FDM特性传输特性方面有独特方便之处,利用它集数值分析、矩阵运算、信号处理和图形显示于一体,构成了一个方便的、界面和谐的优势,通过对维稳定电流场模型进行仿真实验,仿真结果恰好验证了Matlab在分析微带线FDM特性传输特性具有优势,且方法切实可行。
Matlab;维稳定电流场模型;微带线FDM特性;有限差分法
Matlab是一个为科学和工程计算而专门设计的高级交互式的软件包。它集数值分析、矩阵运算、信号处理和图形显示于一体,构成了一个方便的、界面和谐的用户环境。运作在这样的环境下,对用户所要的问题,用户只需列出简单的数学表达式,其结果便以数值或图形方式呈现出来。
Matlab中有大量的命令和事先定义的可用函数集,也可通称为Matlab的M文件,这就使得用它来求解问题通常的传统编程远慢与该种方式;还有一点也是其最重要的特点,易于扩展。它允许用户创建自己的文件来完成M的分配的功能,构成适合工具箱的其他领域[1]。
解决高频电磁波的传输问题是解决微电子技术的重大课题,由于在传输过程中稳定性差、衰减快,并且宽频带的电磁波在传输过程中容易发生畸变和扭曲,因而分析探讨微带线上传播是一个重要研究课题;利用Matlab具有强大的报表功能的语言,是其他语言所无法比拟的;例如,一个语句可以在指定的FFT数据的快速傅立叶变换完成,这是几十相当于或甚至C语言上百的Fortran语言的语句;此外,节目爱好者梦寐以求快速、灵巧、转换快的客户要求,为Matlab提供了一个良好的用户群体,许多功能会自动绘制图形本身,并会自动选择坐标刻度[2];正因为此强大的优点,用它来分析微带线FDM的特性,是抽象的的电磁理论变为可直观的、可测的图像,对我们进一步探讨电磁场对物质作用大有裨益。
1 微带线上传播的电磁理论分析
所谓微带线,就是适合制作微波集成电路的平面结构传输线。微带线是一种带状导线,与地平面之间用一种电介质隔离开,其另一面直接接触空气,只有只有一个地平面作为参考层面。微带线的几何结构和电场力线图如图1所示,它包括导体板、介质基片和导体带3部分。介质基片必须损耗小、光洁度高,以降低衰减。微带线的几何结构并不复杂,但是它的电场磁场却相当复杂,在微带线上传输的并不是严格的TEM波,而是准TEM波。由于介质基片的存在,场的能量主要集中在基片区域,其场分布与TEM波非常接近,故称为准TEM波。
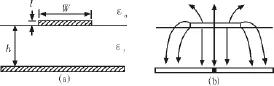
图1 微带线的几何结构和电场力线图
假如我们只做近似考虑,则微带线上传播的电磁可近似看成TEM波,它的特性阻抗就能用下面的公式计算:

式中C、L分别为微带线单位长度的电容和电感,v为波在线上传播的速度。如假定线上不存在介质时单位长度的电容为C0,由于传感线的电感L由本身的性质决定,它将不会因为电介质的存在与否而改变。又因介质不存在时线上波的传播速度为光速vc,而且

由这个式子可解出L

将这个L值代入(1)式就求出了微带线的特性阻抗Z0为

从上面的公式可见,求微带线特性阻抗的关键在于分别求出介质存在和不存在时,线上的单位长度电容C和C0,求这些电容的方法有两种[3]:
1)先用差分法求出微带线横截面内电位分布后,再求内导体(或外导体)单位长度上的总电荷量Q,为求这个Q值,不妨我们取一个如图1(a)中虚线所示的任意的包围内导体的面A。这个在面的每个边均通过网格节点并平行于坐标轴。其中一个边上任意点p处的电通量法向分量Dn应等于

Dn可用p处邻的网格节点e,f处的电位差表示(见图1(b))
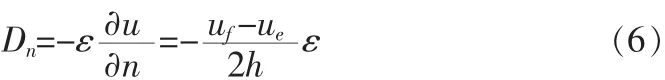
我们在线上取一个如图2所示的体积V,它在线的纵z向方向等于1,而横截面就是A面,将Dn对这个体积的表面S积分,根据高斯定律,它应等于内导体表面上单位长度的电荷Q,即是

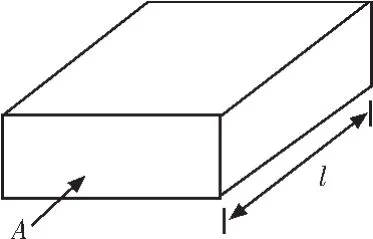
图2 包围内导体的体积
因为要求的是静电电容,线内电场将不随坐标改变而改变[4];考虑到线上纵向电场,本质上没有电通量穿过前、后两个面,这时上面的积分形式简化为下面的形式
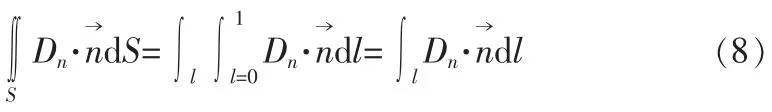
式中l表示面积A的周边。

图3 包围内的导体
设面积A的4个边每边包括nm个节点,m=1,2,3,4,又式(8)右边的线积分可分成对4个边的积分,再对每个边的积分利用梯形数值积分法求积,根据式(7)和(8)
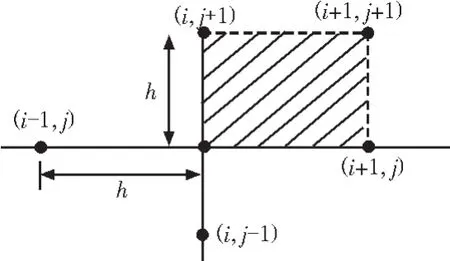
图4 由四个网格节点形成的小区
就可得到下面的求Q公式
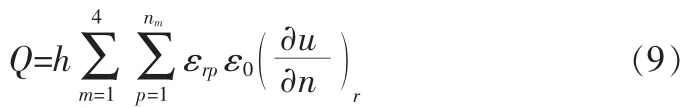
式中εrp代表节点p处的相对介电常数值,符号Σ′表示和的第一项和第末项乘以0.5。如果令微带线内导体电位为1 V,外导体电位为零,则待求的线的单位长度电容为

2)不妨设线的内、外导体之间电位差ua为1 V,用差分法求出横截面上的电位分布,根据电场分布就能可求得到线上单位长度储藏的电能为Wc,这时要求的电容C可按下式求解:
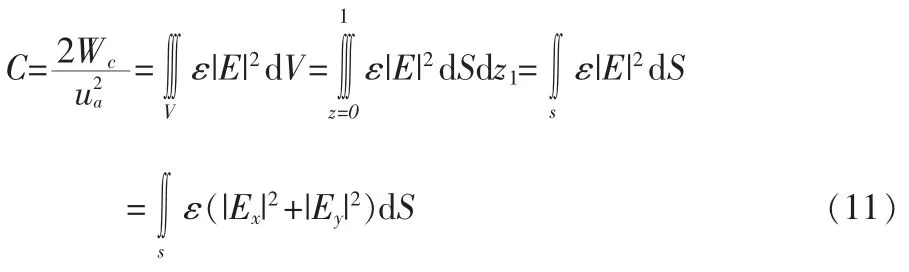
上式中利用了电场E不是z的函数关系,对S的面积分是在线的横截面上进行。
2 利用差分法求解微带线问题例析
在微波领域的很多实际应用过程中,场域中除空气外还可能填充有别的介质,微带线就是这种情况。当用差分法处理这类问题时,就需要导出两种交界面处的差分格式。下面就来讨论如图5所示的相对介电常数分别为εr1和εr2的两种介质交界面处的情况。因空间不存在自由电荷,所以无论在那种介质的内部区域都满足拉普拉斯方程[6],因此它们内部节点电位的计算仍由(12)

式决定。在介质的交界面处,由于电通量的连续性,公式(13)成立。

图5 介质的不同分层

以公式(13)为基础,就可导出介质分层处的差分格式。为了这个目的,在图5中绘出了一个中心落在交界面,尺寸和网格尺寸相同的网格S,在这个网格区域,对式(13)进行面积分。并利用两维高斯定律可得
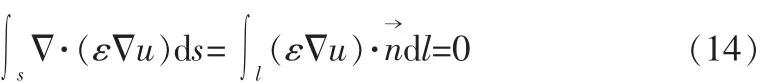
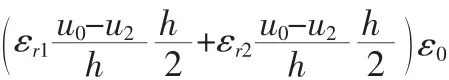
式中ε0自由空间的介电常数,εr1,εr2分别为两种介质的相对介电常数[7]。
对其余的3个边,可以获得类似的公式。将它们加起来就有整理后就得到:
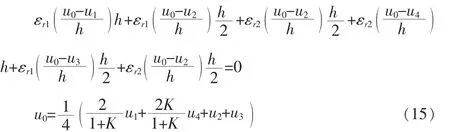
式中K=εr2/εr1,有兴趣的是εr1=1,即一种介质是空气的情况,这时K=εr2,上式就成为

利用同样的分析方法可以求出图6所示的介质交界面角处电位u0。
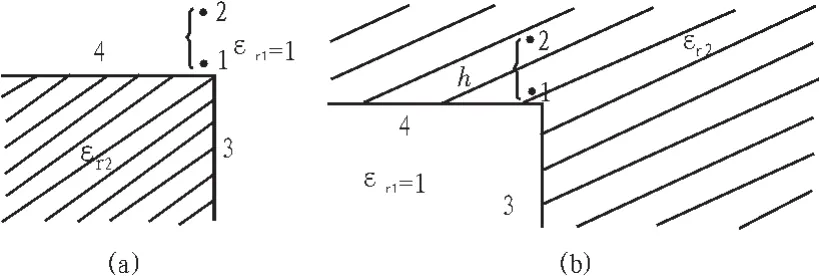
图6 具有角点两介质交界层
对图6(a)情况
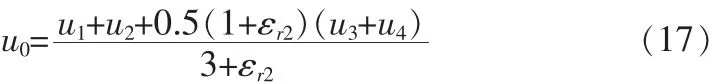
对图6(b)情况

3 整个用差分法求解微带线问题的计算框图设计
根据以上理论分析,只要建立合适数学模型,用差分法求解微带线问题就可以用下面的计算框图进行计算,其方框图如图7所示。
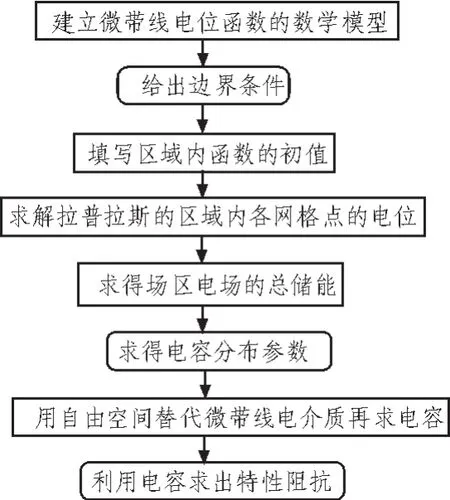
图7 求解微带线特性阻抗的计算方框图
4 数值计算结果及讨论
4.1屏蔽单微带线屏蔽单微带网格划分如图8所示,根据具有屏蔽盒的微带线的结构,假定微带线电位为1 V,屏蔽盒电位为零。微带线宽w=10 mm,介质厚度t=10 mm。屏蔽盒宽取a=50 mm,高取b=30 mm,填充介质的相对介电常数εr=9.6,图8中黑点表示填充的电介质。S为微带线左边界到屏蔽盒边界的距离[7]。
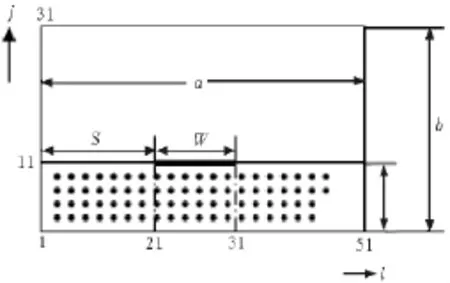
图8 单微带线网格剖分图
4.2电位分布及特性阻抗
对微带线电场进行模拟,得到在屏蔽区域内的电位,用Matlab画出电位分布如图9、图10所示。

图9 单微带线场强分布图

图10 单微带线等势线图
由图9可以直观地看出场强分布情况:从场强中的颜色差可以看出从微带线周围延伸,颜色逐渐由红色变蓝,由色差表可以看出,即图9中由上向下场强由强变弱所以可以得出微带线附近场强较强。可以由等势线图直观的看出从微带线处开始向四周等位线变疏,即电场减弱,而且等位线成近似对称分布[8]。
求出电位分布后,再求出电位的梯度,即得电场强度分布。而高斯定理是对于一个闭合曲面的积分,因此此处利用数值积分法,利用式可以求得微带线的特性阻抗为:当w/t=1.0时,Z0=46.076 Ω。
5 结束语
Matlab在有限差分法的计算中,或者说是在工程计算和数据处理中,具备如下优点[10]:
1)比其他高级编程语言,Matlab编程语言更接近数学表达式;
2)语句简洁明了,表现出独到的功能;
3)有大量的数据处理过程,避免变量之前定义的矩阵,Matlab会自动获取所需的存储空间;
4)提供了一个良好的用户界面,许多功能会自动绘制图形本身,并会自动选择坐标刻度设计,可以让用户大大节省了时间,提高了设计质量。综上所述Matlab工具软件在数据的处理和结果成图方面都是极具潜力的。
[1]胡昆明,李升高,王晖.天线方向行测量系统设计与实现[J].电子测量技术技术,2012,35(1):112-115.
[2]段虎,李益华.小波变换在电力系统谐波检测方面的应用[J].国外电子测量技术,2010,29(12):73-75.
[3]王刚,黄飞,乔纯捷.具备时间统一支持的网络智能传感器设计[J].电子测量与仪器学报,2008,22(6):112-116.
[4]曹丹华,吴裕斌,阮玉.磁光存储系统数据信道误码特性分析[J].电子学报,1996(24):107-110.
[5]张达,金立军.基于频谱细化与差值法的特征谐波分析研究[J].电子测量与仪器学报,2013,27(4):298-304.
[5]唐求,王耀南,郭斯羽,等.基于S变换与PNN的电能质量多扰检测[J].仪器仪表学报,2009,30(8):1668-1673.
[7]张丽.许海电力系统测控装置的抗干扰技术研究[J].国外电子测量技术,2008,27(7):69-70.
Microstrip line FDM transmission characteristics analysis
LIU Bing-an1,LIU Qing2
(1.Shaanxi Polytechnic Institute,Xianyang 712000,China;2.Shaanxi Institute of International Trade,Xianyang 712000,China)
In order to explore transmission characteristics of microstrip line FDM,the Matlab was applied to forward modeling calculation of finite difference method,give full play to the function of its powerful and convenient.By the model of twodimensional steady current field trial showed that the Matlab in studying the characteristics of microstrip line FDM has unique convenient transmission characteristics,use it to set numerical analysis,matrix computation,signal processing and graphic display at an organic whole,constitute a convenient,the advantages of harmonious interface,through the simulation experiment of d steady current field model,the simulation results to prove the Matlab FDM based on the analysis of microstrip line transmission characteristics method has advantages and practical.
Matlab;model of the steady current field;FDM microstrip line features;finite difference method
TN011
A
1674-6236(2016)12-0124-04
2015-05-06稿件编号:201505037
刘秉安(1962—),男,陕西彬县人,副教授。研究方向:电子电工教学和研究。

