基于改进增益型自适应LMS算法的谐波检测方法

王洪诚，王 蕾，沈 霞，杨欣荣，王 正



基于改进增益型自适应LMS算法的谐波检测方法

王洪诚1，王 蕾2，沈 霞1，杨欣荣2，王 正2

(1.西南石油大学电气信息学院，四川 成都 610500；2.西南石油大学机电工程学院，四川 成都 610500)

基于自适应噪声对消原理的谐波电流检测方法相对其他检测方法来说，具有实现简单、鲁棒性强等特点。该方法利用信号处理中的自适应干扰对消原理，将电网电压信号作为参考输入，负载电流作为原始输入，从负载中实时消除与电压波形相同的基波有功电流分量(或基波电流)，从而得到负载电流中所有谐波与基波电流无功分量之和。再配合有源电力滤波器(APF)，由补偿装置注入一个与谐波和基波电流无功分量之和大小相等极性相反的补偿电流，达到抑制谐波与基波电流无功分量的目的。提出了一种基于改进增益型自适应谐波电流的检测方法，该方法采用的反馈量不同于以往方法中的误差信号，而是将误差信号经过数学转换，使其转换成一个能真正反映系统跟踪误差的信号，并将其作为自适应滤波器权系数迭代的反馈量。通过Matlab证明该方法能够在保持较小的稳态失调的情况下也具有较快的动态响应速度。

自适应算法；谐波电流检测；最小均方算法；自适应噪声对消技术；有源电力滤波器

0 引言

随着大量非线性负载的投入使用，谐波污染已经对电力系统和用电设备的安全与稳定运行构成严重威胁。为了有效地治理谐波污染，一系列谐波电流检测方法相继被提出，主要有基于瞬时无功功率理论[1]、FFT变换[2-3]、pq理论[4-5]以及小波变换[6-8]等。这些方法在一定程度上促进了谐波电流检测方法的进步，但它们本身固有的一些缺点使其在实际应用中受到了限制[9]。

由于自适应谐波电流检测方法具有实现简单，鲁棒性强，且在单相以及三相电力系统中具有通用性等特点，使得该方法越来越吸引广大国内外研究者的关注[10-12]。自适应谐波检测方法主要有基于ANCT和基于ADALINE这两种检测模型，自适应谐波电流检测算法主要有最小均方(LMS)算法和递归最小二乘法(RLS)[9]。传统的基于ANCT模型的LMS算法的步长控制着算法的收敛速度与稳态误差，步长越大，其算法的收敛速度越快，而稳态误差也越大；步长越小，其收敛速度越慢，稳态误差也越小。因此，为兼顾算法的收敛速度与稳态误差，变步长的LMS算法也相继被提出[13-15]。本文基于ANCT模型的变步长LMS算法，提出了一种改进型算法，将真正能反映跟踪误差的信号作为自适应反馈量。对改进算法进行Matlab仿真，将仿真结果与传统算法进行比较，证明改进算法的优越性。

1 基于ANCT的检测模型

非线性负载电流傅里叶级数展开形式如式(1)。

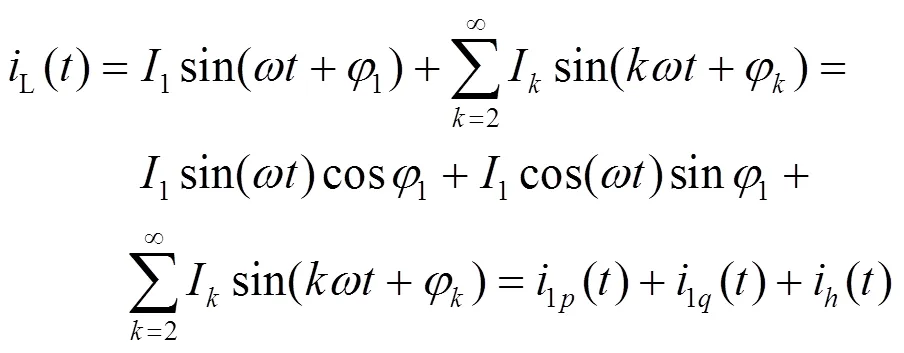
其中：=1, 2, …表示谐波次数；1p()是基波电流有功分量，1q()为基波电流无功分量；h()为谐波分量。若对电力系统同时进行谐波抑制与无功补偿，则式(1)中1p()作为被跟踪信号；若对电力系统只进行谐波抑制，则被跟踪对象便是基波电流1()。基于ANCT模型的自适应滤波原理框图如图1所示。

如图1，跟踪对象为1p()，第时刻基波有功分量为1p()，d()为谐波与基波无功分量的总和。

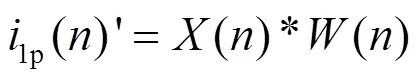
(3)

图1 基于ANCT的自适应滤波原理框图

Fig.1 Block diagram of adaptive filter based on ANCT

根据自适应滤波原理框图，采用最小均方(LMS)算法，其迭代公式如下：

(5)

式中：()为时刻参考输入信号；*()为系统权系数，()为自适应滤波器权系数；为步长因子。

该模型的滤波原理是，根据反馈的误差信号()来调整自适应滤波器权系数()，经过迭代使得()等于*()，即1p()′为滤波器输出信号，实时跟踪1p()的变化，使得d()′等于d()，得到APF需要的各次谐波与基波无功分量的总和。

2 ANCT模型中改进的自适应LMS算法

假设电源电压为理想无畸变波形，如式(6)。

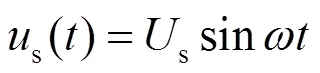
由式(1)可知：

(7)

由图1可知

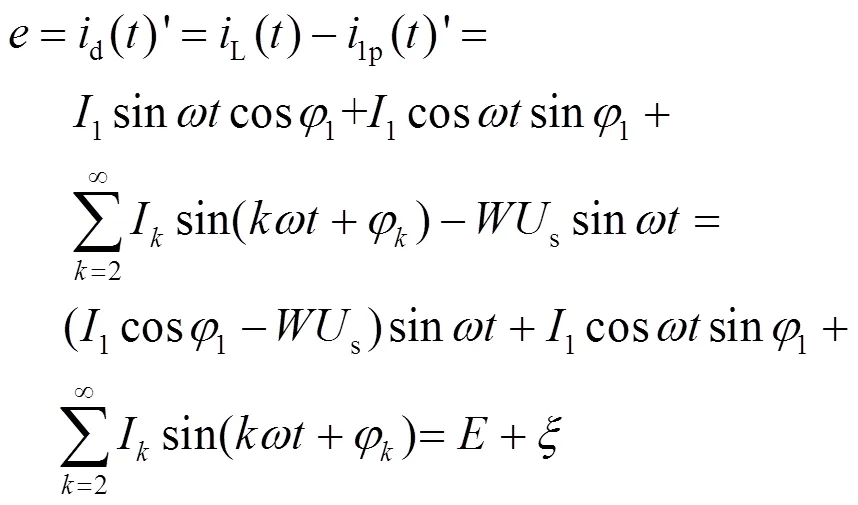
从上式可看出，要使得1p()′跟踪1p()，误差信号并不是直接反映跟踪情况的反馈量，而才是真正反映跟踪情况的误差信号。将式(8)等号两边同时乘以，得到

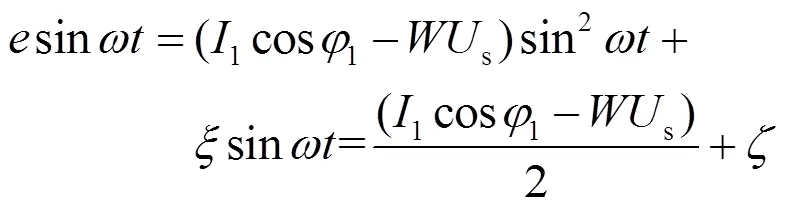
其中，为交流干扰信号，且其最小频率也为基波的两倍，所以，对式(9)等号两边进行积分，积分范围为电网周期的一半，在1/2个电网周期内积分为零[16]。

(10)

整理后即得

(12)

假设

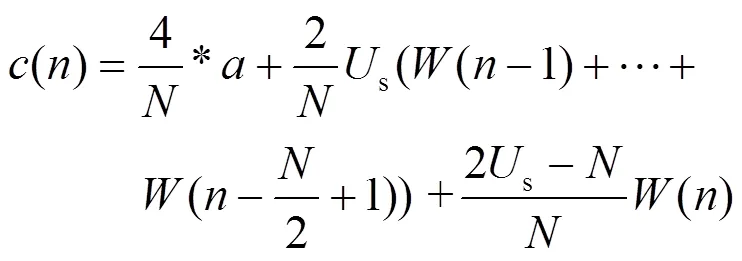
其中，为一个周期内采样点数。由上式可知，反馈量应为()，而自适应谐波检测跟踪波形的最终目的是使得1p()′等于1p()，又因为

(14)

所以，跟踪的最终目的是

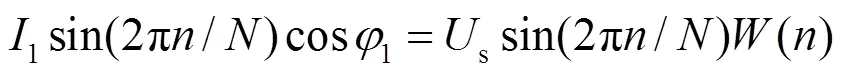
整理得

(16)

所以，由式(12)、式(13)可知

其中，为步长，且上式中()只是一个变量，也就是说，自适应滤波器为一阶滤波器。

3 仿真实验分析

在以上研究的基础上，运用仿真软件Matlab对算法进行仿真验证。

图2 负载电流波形

假设负载电流如下：

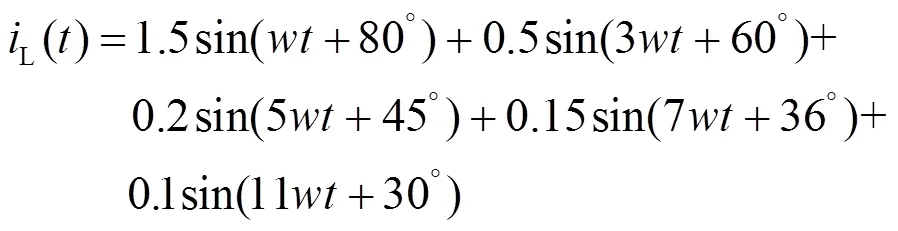
输入信号：

(19)

设采样频率为10 000 Hz，基波频率为50 Hz。图2为负载电流L的波形图。

3.1 比较不同步长时的1p()跟踪情况

如图3(a)、图3(b)分别是步长为0.1和0.05时的基波电流有功分量的跟踪情况，比较图3(a)、图3 (b)可看出，当步长为0.05时的跟踪情况优于步长为0.1时的跟踪情况。

图4(a)、图4 (b)分别为步长为0.1和0.05时误差变化情况，图中显示在=0.01 s之后，步长为0.05时的误差要小于步长为0.1时的误差，且稳定性也更好。经调试发现，当步长为0.041 56时，其跟踪情况比步长为0.05时更优。

图3 不同步长时基波有功分量跟踪情况

3.2 负载电流发生突变时的跟踪情况

图5为负载电流在=0.03 s时刻发生突变的波形。图6为当负载电流发生突变，步长=0.041 56，时的基波电流有功分量跟踪波形图。

该算法中，对每个采样点与该采样点的一个电网周期前的对应点(即采样点的第(-)个)进行比较，如果两个点的数值相等，则电流信号未发生突变；若不相等，则此时信号发生突变，对()置零，算法从头开始迭代。从图6可以看出，即使负载电流发生突变也可以快速跟踪到基波有功分量，说明该算法鲁棒性较强。

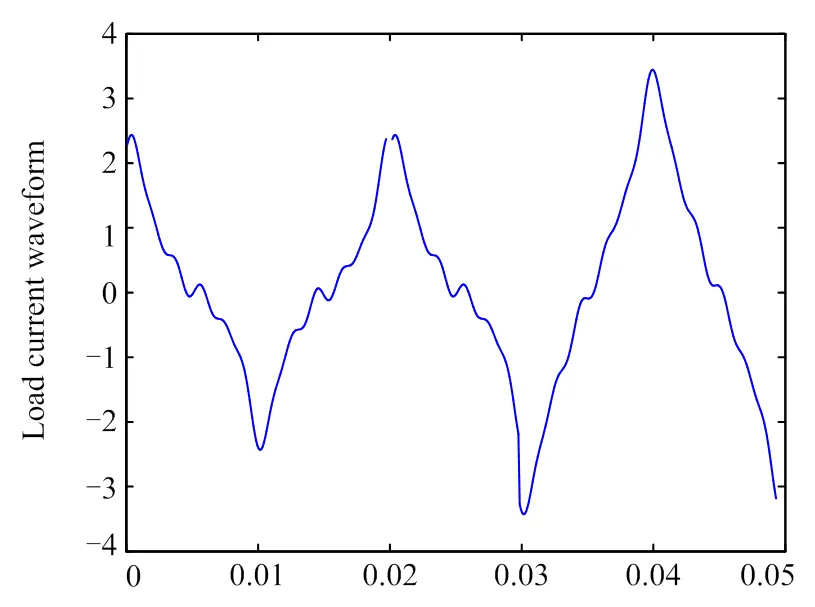
图5 负载电流在t=0.03秒时发生突变

图6 负载电流突变时的跟踪情况

3.3 不同信噪比时跟踪情况

图7为当固定步长为0.041 56且基波有功分量幅值为50时的跟踪情况，图中可看出，即使基波有功分量幅值由1.5增至50，其跟踪曲线也是在=0.01 s起与理想曲线趋于重合。

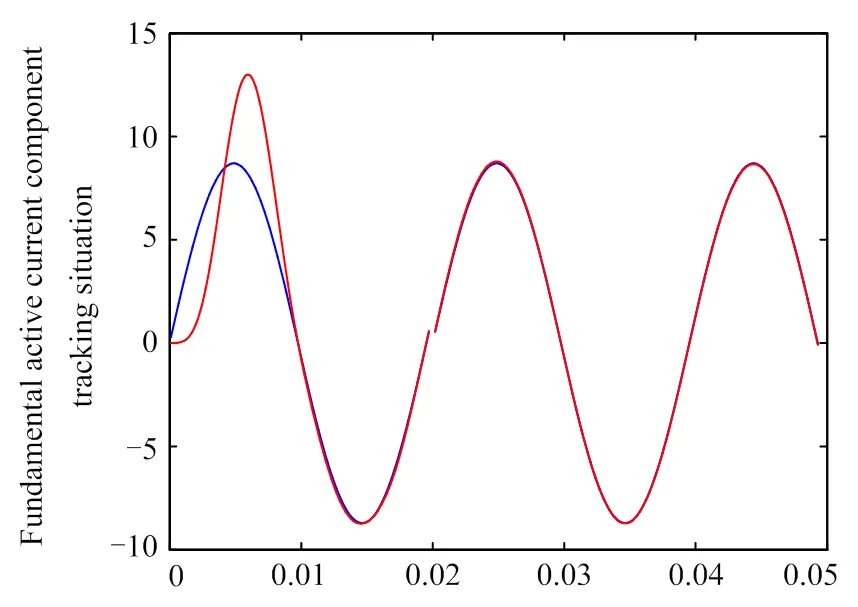
图7 当固定步长为0.041 56时且基波有功分量幅值为50时的跟踪情况

4 结论

(1) 为了更好地提高自适应滤波算法的性能，提出了基于改进增益型自适应谐波检测方法，这种方法能同时获得良好的收敛速度与稳态精度；

(2) 算法鲁棒性较强，能较好地适应不稳定负载电流的情况；

(3) 该方法与以往变步长算法相比减少了大量的计算量；

(4) 由仿真实验结果可看出，即使在信号发生突变或信噪比不同的时候，该算法也能很好地跟踪目标信号；

(5) 该算法收敛后的误差与步长大小及负载电流基波有功分量幅值有关，还有改进的空间。

[1] 张俊敏, 田微. 基于瞬时无功功率理论谐波检测方法的研究[J]. 电力系统保护与控制, 2008, 36(18): 33-36.

ZHANG Junmin, TIAN Wei. The research on harmonic detection method based on instantaneous reactive power theory[J]. Power System Protection and Control, 2008, 36(18): 33-36.

[2] 翟瑞淼, 英超, 任国臣, 等. 基于Nuttall窗的三峰插值谐波算法分析[J]. 电力系统保护与控制, 2015, 43(10): 38-43.

ZHAI Ruimiao, YING Chao, REN Guocheng, et al. An approach for harmonic analysis based on Nuttall window and triple-spectral-line interpolation[J]. Power System Protection and Control, 2015, 43(10): 38-43.

[3] 郝柱, 顾伟, 褚建新, 等. 基于四谱线插值FFT的电网谐波检测方法[J]. 电力系统保护与控制, 2014, 42(19): 107-113.

HAO Zhu, GU Wei, CHU Jianxin, et al. A harmonic detection method based on FFT with interpolation by four lines[J]. Power System Protection and Control, 2014, 42(19): 107-113.

[4] 荣海舟, 粟时平, 逯培兵, 等. 基于ip-iq法的谐波数字检测研究[J]. 长沙理工大学学报(自然科学版), 2007, 4(3): 54-57.

RONG Haizhou, SU Shiping, LU Peibing, et al. Digital detection of harmonic based on ip-iq theory[J]. Changsha University of Technology(Natural Science), 2007, 4(3): 54-57.

[5] 郑征, 杜翠静, 常万仓. 三相不对称系统中谐波电流检测的新方法[J]. 电力系统及其自动化学报, 2010, 22(3): 50-54.

ZHENG Zheng, DU Cuijing, CHANG Wancang. A new method of harmonic current detection in asymmetric three-phase system[J]. Proceedings of the CSU-EPSA, 2010, 22(3): 50-54.

[6] 陈欢, 何怡刚, 肖建平, 等. 基于CWT和DWT相结合的谐波检测[J]. 电力系统保护与控制, 2015, 43(20): 71-75.

CHEN Huan, HE Yigang, XIAO Jianping, et al. Harmonic detection based on a combination of continuous wavelet transform and discrete wavelet transform[J]. Power System Protection and Control, 2015, 43(20): 71-75.

[7] 周林, 夏雪, 万蕴杰, 等. 基于小波变换的谐波测量方法综述[J]. 电工技术学报, 2006, 21(9): 67-74.

ZHOU Lin, XIA Xue, WAN Yunjie, et al. Review of harmonic current detection based on wavelet transform[J]. Transactions of China Electrotechnical Society, 2006, 21(9): 67-74.

[8] 李正明, 徐敏, 潘天红, 等. 基于小波变换和HHT的分布式并网系统谐波检测方法[J]. 电力系统保护与控制, 2014, 42(4): 34-39.

LI Zhengming, XU Min, PAN Tianhong, et al. A harmonic detection method for distributed connected grid system by using wavelet transform and HHT[J]. Power System Protection and Control, 2014, 42(4): 34-39.

[9] 喻翌, 赵海全, 何正友. 基于ANCT和ADALINE两种自适应谐波电流检测模型的分析[J]. 电力系统保护与控制, 2013, 41(16): 71-77.

YU Yi, ZHAO Haiquan, HE Zhengyou. An analysis of two models based on ANCT and ADALINE in adaptive harmonic current detection[J]. Power System Protection and Control, 2013, 41(16): 71-77.

[10]王群, 吴宁, 谢品芳. 一种基于神经元的自适应谐波电流检测法[J]. 电力系统自动化, 1997, 21(10): 13-16.

WANG Qun, WU Ning, XIE Pinfang. An adaptive harmonic current detection method based on neuron[J]. Automation of Electric Power Systems, 1997, 21(10): 13-16.

[11]王群, 谢品芳, 吴宁, 等. 模拟电路实现的神经元自适应谐波电流检测方法[J]. 中国电机工程学报, 1999, 19(6): 42-46.

WANG Qun, XIE Pinfang, WU Ning, et al. An adaptive harmonic current detection method based on neuron taking use of artificial circuit[J]. Proceedings of the CSEE, 1999, 19(6): 42-46.

[12] 高大威, 孙孝瑞. 基于自适应线性神经元网络的三相畸变电流检测方法及实现[J]. 中国电机工程学报, 2001, 21(3): 49-52.

GAO Dawei, SUN Xiaorui. The three phase distortion current detection method and realization based on adaptive linear neural network[J]. Proceedings of the CSEE, 2001, 21(3): 49-52.

[13] KWONG R H, JOHNSTON E W. A variable step size LMS algorithm[J]. IEEE Transactions on Signal Processing, 1992, 40(7):1633-1642.

[14]高鹰, 谢胜利. 一种变步长LMS自适应滤波算法及分析[J]. 电子学报, 2001, 29(8): 1094-1097.

GAO Ying, XIE Shengli. An adaptive filtering algorithm based on variable step size LMS and its realization[J]. Journal of Electronics, 2001, 29(8): 1094-1097.

[15]李辉, 吴正国, 邹云屏, 等. 变步长自适应算法在有源滤波器谐波检测中的应用[J]. 中国电机工程学报, 2006, 26(9): 99-103.

LI Hui, WU Zhengguo, ZOU Yunping, et al. The applicationof adaptive algorithm based on variable step size in harmonicdetection of the active filter[J]. Proceedings of the CSEE, 2006, 26(9): 99-103.

[16]何娜, 黄丽娜, 武健, 等. 一种新型快速自适应谐波检测算法[J]. 中国电机工程学报, 2008, 28(22): 124-129.

HE Na, HUANG Lina, WU Jian, et al. A newly fast adaptive harmonic detection algorithm[J]. Proceedings of the CSEE, 2008, 28(22): 124-129.

(编辑 姜新丽)

New harmonic detection method based on LMS algorithm of improved adaptive gain

WANG Hongcheng1, WANG Lei2, SHEN Xia1, YANG Xinrong2, WANG Zheng2

(1. School of Electrical Information, Southwest Petroleum University, Chengdu 610500, China; 2. School of Mechanical and Electrical Engineering, Southwest Petroleum University, Chengdu 610500, China)

Compared with other detection method, harmonic detection method based on adaptive noise cancellation principle has the advantages like being easier to achieve, strong robustness and so on. This method uses the principle of adaptive interference cancellation in signal processing, takes the grid voltage signal as the reference input and the load current as the original input, eliminates the fundamental active current waveform that is similar to the voltage waveform in the real time from the load current, gets the sum of harmonic and fundamental reactive current, injects a compensation current that has the same value and the reverse polar with the sum of harmonic and fundamental reactive current to load current through compensation device of APF, and then achieve the purpose to suppress harmonic and fundamental reactive current. This paper proposes a new harmonic detection method based on LMS algorithm of improved adaptive gain. What this new method takes as feedback is different from previous researches. Previous studies use the error as feedback, but this new research's feedback is the change form of the error which is the true signal to reflect the system's tracking situation, and this feedback is used to the iterative process of the adaptive filter's weight coefficient. This new method is proved through the MATLAB simulation that it is able to keep small steady state error also has faster dynamic response speed.

adaptive algorithm; harmonic detection method; LMS algorithm; ANCT; APF

10.7667/PSPC150795

2015-05-12；

2015-11-10

王洪诚(1955-)，男，教授，研究生导师，研究方向为控制科学与工程； 王 蕾(1990-)，女，硕士研究生，研究方向为电力系统谐波检测与抑制方法；E-mail:15198243251@163.com 沈 霞(1981-)，女，讲师，研究方向为电力电子与电力传动。