PMSG风力发电系统转速估计算法的研究

程 辉，杨克立，王克军，李 娜



PMSG风力发电系统转速估计算法的研究

程 辉1，杨克立2，王克军1，李 娜1

(1.河南工程学院电气信息工程学院，河南 郑州 451192; 2.中原工学院工业训练中心，河南 郑州 450007)

提出了一种无传感器直驱式永磁同步风力发电机控制系统的转子速度估算法。该算法可由简单的定子磁通方程推导，且只需检测定子电压和电流。定子磁通估算通过基于定子电压模型的可编程低通滤波器而设计，建立了基于递归最小二乘法的电机转速辨识模型，并将实时辨识的电机转速用于转子位置观测和转子磁场定向矢量控制。仿真结果表明，实现了最大功率跟踪控制，验证了控制算法的有效性和可行性。

永磁同步发电机；转速估计；风力发电系统；无传感器；最大功率跟踪控制

0 引言

风力发电系统主要有恒速恒频风力发电系统和变速恒频风力发电系统两大类，后者使用永磁同步发电机，可在很宽的风速变化范围内实现最大风能捕获，具有高功率密度，且无需齿轮箱和滑环及励磁装置[1]，结构简单，可靠性高，是未来风力发电技术发展的主要趋势之一。

风能的不确定性以及风力机自身特性会使风力发电机输出功率随风速变化而波动。为了提高风能的利用效率，最大程度捕获风能，需使风力机在任意风速时都能运行在最佳转速，为此需要进行高精度的风速检测和转速检测，但也降低了系统运行的可靠性，另外，风力机周围气流受叶片扰动较大，难以准确测量当前有效风速[2]。与此同时，定子电流和定子电压的准确测量可用于转速估算，从而无需进行转速测量。目前，国内外学者对直驱式PMSG无速度传感器矢量控制进行了大量的研究。对永磁同步电机位置和转速估算较为成熟的方法有高频信号注入法和基于反电势估算法。前者利用电机的凸极效应具有较强的鲁棒性，特别适合于零速启动和低速运行，但是只适用于具有凸极效应的电机，并且注入的高频信号会使电机损耗、转矩波动及噪声变大，电机的动态性能变差；后者是从测量电机的发电动势入手，算法实现较为简单，但由于低速下电机的反电动势值较小，且易受系统测量误差的影响，效果不够理想[3-4]。此外，文献[5]提出了引入软件锁相环的控制策略，通过锁相环得到风力机的转速，但由于发电机输出电压信号中夹杂有部分谐波分量等影响相位锁定的精度。文献[6-7]提出扩展卡尔曼滤波算法，但由于计算量很大需要利用高精度的数字信号处理器来实现实时控制，工程上不宜实现。除了采用基于数学模型的方法以外，还可以利用基于人工智能理论进行转子速度的估算[8-10]。

本文针对无速度传感器的PMSG变速风能发电系统提出了一种转速估计矢量控制算法，通过简单的定子磁通模型以进行转速估算，无需测量装置就可以得到风力机转速，通过控制直驱永磁风力发电机的电磁功率来间接控制风力发电机转速以追踪风力机最佳功率曲线实现对最大风能的捕获。文中，转速采用递归最小二乘法的参数估计算法进行实时在线辨识，并将实时辨识的转速应用于PMSG转子位置估计和转子磁场定向矢量控制。定子磁通估算通过基于定子电压模型的可编程低通滤波器PLPF设计，以提高定子磁通的估算性能。

1 风力机特性

由空气动力学可知，风力机从风能中捕获的机械功率为[11]

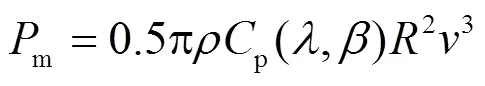
(2)

风力机的功率-转速特性曲线如图1所示。

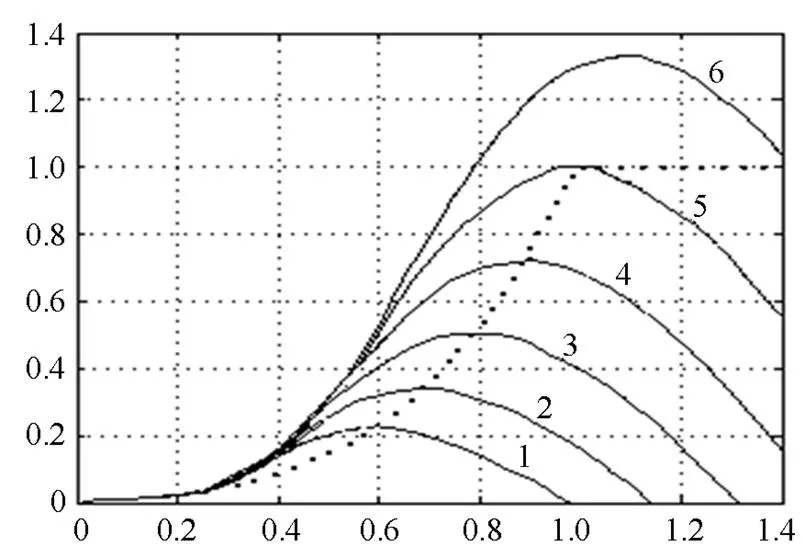
图1 风力机功率-转速特性曲线

2 无传感器PMSG 变速风能发电控制系统

在两相静止坐标系下，表面式PMSM的数学模型[14]可以表示为

(4)

定子磁通(5)

对式(5)求微分并联立式(4)可得：

(7)

由式(7)可知，在定子电流很容易测量获得的基础上，如果定子磁通已知的话转子转速就可以估算出来。

2.1 定子磁通估计

2.2 转子转速估计

重新整理式(7)可得，

本文所辨识的参数是时变的电机转子转速，根据极值定理可以推导出引入遗忘因子的最小二乘法的数学表达式为

(10)

(12)

固定值矩阵的迹

(14)

简化后的恒增益递归最小二乘估算法表达式为

(16)

2.3 机侧变流器控制策略

根据转子磁场定向可得到同步旋转坐标系下PMSG的数学模型为

(19)

机侧变流器的d轴变量和q轴变量间存在耦合，给控制器的设计带来困难，为此采用前馈解耦控制策略。

当PMSM稳定运行时，且忽略定子电阻压降的情况下，电压方程可以简化为

(21)

机侧变流器的矢量控制如图2所示。采用矢量双闭环控制技术。外环为转速环，其速度参考值通过最大功率点跟踪算法给出，调节发电机的电磁转矩，使得实际转速跟踪此参考转速即可捕获最大风能。参考转速与采用估计算法估算的转速进行比较，将其偏差值送入PI调节器即可输出有功电流的参考值；内环分别实现d、q电流的闭环控制，误差信号经PI调节后与各自的解耦补偿项相加得到机侧变流器参考电压，以此进行SVPWM调制。按照单位功率因数控制设定d轴参考电流。

图2 机侧变流器控制系统

2.4 网侧变流器控制策略

在同步旋转dq坐标系下，网侧变换器的数学模型为

(23)

式中：和分别是网侧进线电抗器的电感值和电阻值；和分别是网侧变流器输入三相交流电压的d、q轴分量；和分别为电网侧三相交流电压的d、q轴分量。同样，网侧变流器的d轴变量和q轴变量之间也存在耦合，需要采用前馈解耦控制策略。控制框图如图3所示。

图3 网侧变流器控制系统

3 仿真结果

为了验证文章所提出的控制策略的可行性，利用Matlab/Simulink进行了仿真。建立了无风速无转子转速传感器的PMSG直驱变速风力发电系统，仿真模型如图4所示。图中，机侧以获得额定磁通，网侧以获取单位功率因数。PMSG仿真参数：直流母线电压400 V，电枢绕组交直轴电感为4 mH，每相绕组电阻为0.9，电机极对数为18，电机额定电压为200 V，额定电流11.6 A，额定功率2 kW，额定转速200 r/min。

图4 PMSG风能发电系统

仿真中用到的风速曲线有两种。一种曲线如图5(a)所示，采用理想风，最高风速为9 m/s，最低风速为7 m/s，采用无传感器转子估计算法控制系统的转子速度、功率因数及有功功率输出分别如图5(b)(c)(d)所示。为方便比较起见，图6(a)给出了对应的转子速度及估计的转子速度仿真曲线，图中点划线表示为估计的转子速度，实线为实际转子速度；图6(b)为两者速度误差曲线。

图5 理想风速下无传感器PMSG风能发电系统仿真结果

图6 转速和估计转速波形

从图中可以看出，估计风速和实际风速误差的最大值为0.64 rad/s，控制的效果非常理想。

如图7(a)所示为自然风速曲线，采用无传感器转子估计算法控制系统的转子速度、功率因数及有功功率输出分别如图7(b)(c)(d)所示。为方便比较起见，图8(a)给出了对应的转子速度及估计的转子速度仿真曲线，图中点划线表示为估计的转子速度，实线为实际转子速度；图8(b)为两者速度误差曲线。

图7 自然风速下无传感器PMSG风能发电系统仿真结果

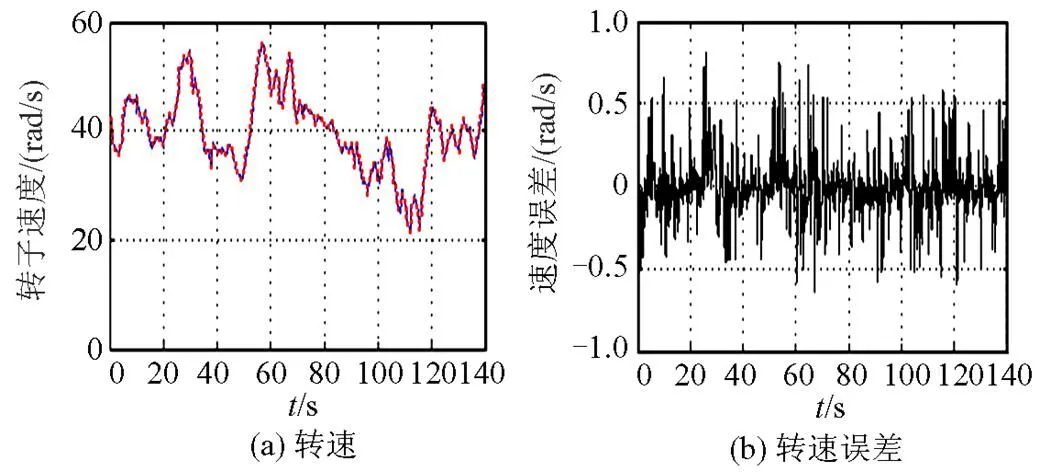
图8 转速和估计转速波形

从图8可以看出，通过定子磁通估算转子速度跟踪风力转速效果良好，估计风速和实际风速误差的最大值为0.83 rad/s。结果表明，本文提出的转子速度估计算法准确度较高，控制效果较好。

4 结论

本文研究了PMSG风力发电系统的转子速度估算法，无需测量风速和风力机转速就可以实现风能的最大功率跟踪。该算法通过简单的定子磁通方程推导，定子磁通估算通过基于定子电压模型的可编程低通滤波器设计，利用遗忘因子的递推最小二乘算法对转速进行实时辨识。本文建立了系统的数学模型，详细进行了系统的设计，并进行了仿真验证，验证了算法的正确性和可行性。

[1] 陈家伟, 陈杰, 龚春英. 变速风力发电系统瞬态载荷分析及其优化设计途径[J]. 电工技术学报, 2015, 30(4): 233-240.

CHEN Jiawei, CHEN Jie, GONG Chunying. Way to optimally design transient load of variable-speed wind energy conversion system[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 233-240.

[2] 马卫东. 风力发电机组最大功率追踪[J]. 高压电器, 2012, 48(7): 57-65.

MA Weidong. Maximum power point tracking for wind turbine[J]. High Voltage Apparatus, 2012, 48(7): 57-65.

[3] 樊继永. 基于EKF的电动车用无刷直流电机无传感器运行[J]. 微特电机, 2011, 39(6): 9-11, 14.

FAN Jiyong. The operation of sensorless BLDCM used in E-bike based on EKF[J]. Small & Special Electrical Machines, 2011, 39(6): 9-11, 14.

[4] YANG Junyou, ZHAO Jingming, QIN Chengzhi, et al. Model reference adaptive sensorless control for surface permanent magnet synchronous machine under severe starting conditions[C] // Power Electronics and Motion Control Conference, 2004: 1018-1022.

[5] 张安安, 郭红鼎, 于兵, 等. 一种风电机组在低风速区间的功率控制方法[J]. 电力系统保护与控制, 2015, 43(23): 84-88.

ZHANG Anan, GUO Hongding, YU Bing, et al. A power control method of wind turbines in low wind speed area[J]. Power System Protection and Control, 2015, 43(23): 84-88.

[6] CHEN Z, TOMITA M, DOKI S, et al. An extended electromotive motive force model for sensorless control of interior permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2003, 50(2): 288-295.

[7] 修春波, 任晓, 李艳晴, 等. 基于卡尔曼滤波的风速序列短期预测方法[J]. 电工技术学报, 2014, 29(2): 254-259.

XIU Chunbo, REN Xiao, LI Yanqing, et al. Short-term prediction method of wind speed series based on Kalman filtering fusion[J]. Transactions of China Electrotechnical Society, 2014, 29(2): 254-259.

[8] 张宇辉, 陈峰, 李慧敏, 等. 基于小波变换和矩阵束算法的同步电机参数辨识[J]. 电力系统保护与控制, 2012, 40(9): 87-92.

ZHANG Yuhui, CHEN Feng, LI Huimin, et al. Parameter identification of synchronous machine based on wavelet transform and matrix pencil algorithm[J]. Power System Protection and Control, 2012, 40(9): 87-92.

[9] 崔双喜, 王维庆, 张强. 风力发电机组独立变桨鲁棒自适应桨距角跟踪控制[J]. 电力系统保护与控制, 2015, 43(6): 52-57.

CUI Shuangxi, WANG Weiqing, ZHANG Qiang. Robust adaptive blade pitch angle tracking control for wind turbines[J]. Power System Protecction and Control, 2015, 43(6): 52-57.

[10]孟令斌, 朱凤龙. 混合电源及功率预测系统在风电并网中的应用[J]. 电力系统保护与控制, 2015, 43(13): 79-85.

MENG Lingbin, ZHU Fenglong. Applications of the mixing power and power forecasting system in wind power[J]. Power System Protecction and Control, 2015, 43(13): 79-85.

[11]张子泳, 胡志坚, 李勇汇, 等. 大型双馈风力发电写小信号动态建模及附加阻尼控制器设计[J]. 电力系统保护与控制, 2011, 39(18): 127-130.

ZHANG Ziyong, HU Zhijian, LI Yonghui, et al. Small signal dynamic modelling and additionaller damping controller designing for large wind generation system based on DFIG[J]. Power System Protecction and Control, 2011, 39(18): 127-130.

[12]何玉林, 吴德俊, 杜静, 等. 风力发电机组的自适应转矩控制及载荷优化[J]. 电网与清洁能源, 2012, 28(3): 79-84.

HE Yulin, WU Dejun, DU Jing, et al. Adaptive torque control and load optimization of wind turbines[J]. Power System and Clean Energy, 2012, 28(3): 79-84.

[13] 年珩, 李嘉文, 万中奇. 基于参数在线辨识的永磁风力发电机无位置传感器控制技术[J]. 中国电机工程学报, 2012, 32(12): 146-153.

NIAN Heng, LI Jiawen, WAN Zhongqi. Sensorless control technique of PMSG for wind power application based on on-line parameter identification[J]. Proceedings of the CSEE, 2012, 32(12): 146-153.

[14]秦斌, 姜学想, 朱万力, 等. 基于无风速传感器的永磁直驱风力发电系统的直接转矩最大功率跟踪控制[J]. 电工技术学报, 2014, 29(1): 132-137.

QIN Bin, JIANG Xuexiang, ZHU Wanli, et al. Maximun power point tracking of PMSG wind turbine system based on the direct torque control without wind speed sensors[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 132-137.

[15] 赵海森, 杜中兰, 刘晓芳, 等. 基于递推最小二乘法与模型参考自适应法的鼠笼式异步电机转子电阻在线辨识方法[J]. 中国电机工程学报, 2014, 34(30): 5386-5394.

ZHAO Haisen, DU Zhonglan, LIU Xiaofang, et al. An on-line identification method for rotor resistance of squirrel cage induction motors based on recursive least square method and model reference adaptive system[J]. Proceedings of the CSEE, 2014, 34(30): 5386-5394.

[16]滕予非, 行武, 张宏图, 等.风力发电系统短路故障特征分析及对保护的影响[J]. 电力系统保护与控制, 2015, 43(19): 29-36.

TENG Yufei, XING Wu, ZHANG Hongtu, et al.Analysis of characteristics of short circuit fault of wind power system and the impact on the protection[J]. Power System Protection and Control, 2015, 43(19): 29-36.

(编辑 张爱琴)

Study on a rotor speed estimation algorithm of PMSG wind power system

CHENG Hui1, YANG Keli2, WANG Kejun1, LI Na1

(1. College of Electrical and Information Engineering, Henan Institute of Engineering, Zhengzhou 451192, China; 2. Training Center for Industry, Zhongyuan University of Technology, Zhengzhou 450007, China)

A rotor speed estimation algorithm in a direct vector controlled permanent magnet synchronous generator wind energy conversion system is proposed. The method is based on a simple equation obtainer from stator voltage and current. Stator flux information required by the speed estimator is obtained using the stator voltage equation by implementing a programmable low pass filter. The constant gain recursive least squares algorithm is adopted. Then, the rotor position obtained based on the proposed method are used in the rotor-flux oriented vector control of PMSG. The simulation result shows that the control strategy realizes maximum power point tracking control, which verifies the validity and feasibility of the theoretical model and control strategy. This work is supported by National Natural Science Foundation of China (No. 61405054).

permanent magnet synchronous generator; speed estimation; wind energy conversion systems; sensorless control; maximum power point tracking control

10.7667/PSPC150739

国家自然科学青年基金项目(61405054)

2015-08-05；

2015-12-20

程 辉(1979-)，女，硕士，讲师，研究方向为电力电子与电力传动、风力发电。E-mail: ch.cxy@163.com