微裂缝内液固两相流动特性研究

杨 倩，陈彦超



微裂缝内液固两相流动特性研究

杨 倩，陈彦超

（东北石油大学， 黑龙江 大庆 163318）

应用欧拉-拉格朗日模型，对微裂缝中液-固两相流动过程进行数值模拟。在数学模型中，液相采用连续相模型，颗粒当做离散分散在连续相中，并考虑了相间耦合作用。对于物理模型，建立了二维直微裂缝模型，研究裂缝的液相粘度、液相速度和颗粒密度等因素对裂缝中两相流动的影响。模拟得到了微通道内颗粒瞬时分布状态、颗粒运动轨迹、颗粒停留时间、颗粒轴向速度分布、液相轴向速度分布等参数的变化规律，定性的揭示了储层裂缝内液固两相流动过程。

微裂缝；计算流体力学；离散元方法；数值模拟

石油主要储存岩石的储集空间中，它是储集油气的场所。储集空间包括粒间孔隙、粒内孔隙、裂缝、溶洞等各种类型的孔、洞、缝，就其形态和分布而论是十分复杂的孔喉网络。储集石油的沉积岩中含有丰富的粘粒矿物，砂岩颗粒以及石英晶体的细小颗粒[1,2]。石油运移时也会对这些微细颗粒有携带的作用，而固体微粒的存在可以影响原油运移的速度和路径。在开采疏松砂岩油藏时，由于地层微粒随石油的流动过程中会发生运移、沉积造成地层损害，使产油量下降，影响油田的正常生产[3]。因此，微粒迁移问题的研究对于疏松砂岩油藏的开发具有非常重要的意义。

如今，微尺度流动已经得到了学者们的广泛关注[4-8]，形成了一个新的学科分支。微观尺度可能会出现与宏观流动不同的规律，并且许多在宏观流动中被忽略的因素，在微流动中可能会成为主要的影响因素。也就是说，当研究对象是微观时，流动的尺度效应就会凸显出来。近年来，大量的对微尺度流动特性的研究表明：常规尺度下的流动关联式因为微通道的许多固有特点而失效，导致基于宏观经验的传统流体力学不再完全适用于微尺度现象，因此，需要对原有的一些规律和理论进行补充和修正[9]。

1 模型的建立

1.1 数学模型

利用Euler-Lagrange方法里的离散元（DEM）模型并结合计算流体动力学（CFD）的相关知识，对裂缝中的液-固两相流动过程进行数值模拟。FLUENT 软件可以在拉氏坐标下模拟流场中离散的第二相。由球形颗粒（代表油滴和砂粒）构成的离散分布在连续相中，计算这些颗粒的轨道以及由颗粒引起的热量或质量传递。液体-颗粒流动遵循质量、动量和牛顿守恒定律［10,11］。

欧拉-拉格朗日模型的关键是计算颗粒的运动轨迹。在两相流动的过程中，每个运动的颗粒都会受到流体以及相邻颗粒对它的作用。因此，可将颗粒的运动分解为随流体运动的悬浮过程和与其他运动颗粒的碰撞过程。

采用计算流体力学和离散单元方法对微裂缝内液固两相流动过程进行了数值模拟。采用-ε模型模拟液体流动，离散单元方法模拟颗粒流动，Huilin- Gidaspow 曳力模型模拟相间作用力。考虑液体速度、粘度以及固体颗粒密度等因素对流动的影响。

1.2 物理模型

如图1所示为裂缝网格划分图 ，依据此图，本论文模拟了水平方向微裂缝内的液固两相流动。具体参数如下：裂缝的长为1 000 μm，宽200 μm。左侧为射流口，出口设为压力出口。

图1 裂缝网格图

液相选择液态水为参数，密度为1 000/m3。入口速度分别为0.1、0.3和0.5 mm/s。砂粒密度选取1 550、2 000和2 500 kg/m3，直径为2 μm。油滴的密度为800 kg/m3，直径为2 μm。流动为非定常流、松弛因子为1、考虑重力影响（9.81 m/s2）。

2 计算结果和分析

2.1 微裂缝内液固两相流动行为分析

图2为Fluent模拟的流体速度为0.1 mm/s，粘度为0.001 kg/m.s算例不同时刻油滴及砂粒颗粒分布图，左侧为入口处，两种颗粒的初始射入速度为0m/s，液体速度为0.1 mm/s。图中可以清楚看出油和砂粒在微裂缝中的分布情况。两种颗粒随液体流动而运移，最后由压力出口流出。两种颗粒均匀混合，未表现出明显的重力作用。

图2 不同时刻颗粒分布图

Fig.2 Particle distribution of different time

图3为流体、油滴及砂粒的速度矢量图，由图可知流体和颗粒运动方向及速度大小。液体的流动是比较有序的，在壁面附近流体出现回流，沿壁面向左运动，在模型中有多处呈旋涡流动状态；对于油滴颗粒来说，颗粒速度较小，在边界处的颗粒碰击壁面速度较大；而固相砂粒的速度相对较大，而且表现出强烈的无序性。

图3 三相速度矢量图

图4分别表示油滴和砂粒运动轨迹图，由图可以看出，颗粒的初始堆积位置不一致，使得不同颗粒的运动轨迹明显不同，但总体趋势是向出口运动。距离射流口较近的位置，颗粒的运动范围较大，这主要是因为入口射流为颗粒提供更大的能量，颗粒更活跃，致使运动范围扩大。

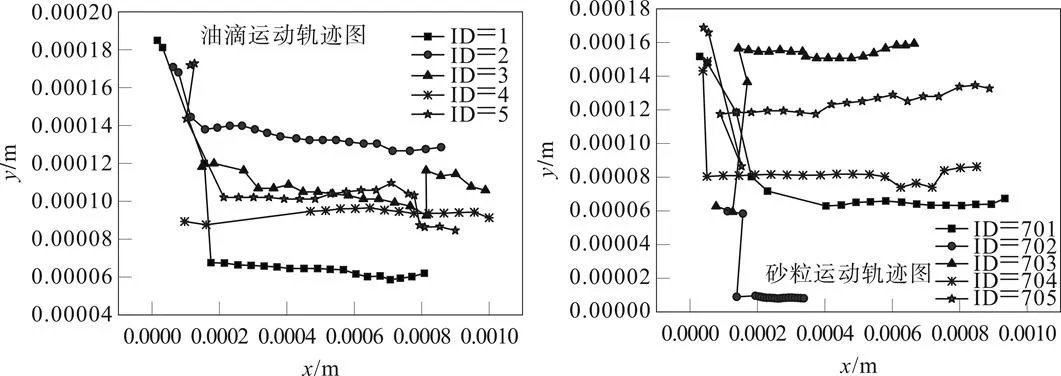
图4 油滴-砂粒运动轨迹

2.2 液相粘度对颗粒流动特性的影响

图5表示在液体速度均为0.1 mm/s条件下，平行于入口距离300 μm直线上液体轴向速度和切向速度沿轴向的分布。随着粘度的增加，液体在中心线处运动剧烈，靠近壁面处速度逐渐降低。颗粒的径向速度受粘度影响较大，并且与粘度大小不成正比，在模型的上部出现负速度，说明液体受重力作用向下运动，形成裂缝内的循环流动。而在接近壁面处变化较小，趋于稳定。

同正：扑鼻的香料、樱桃香气，十分有爆发力。入口酸度有力，带来十分不错的清爽感。酒体中等，单宁柔滑。余味中可可、巧克力香气明显。

图5 不同粘度下液相轴向和切向速度

图6分别是，油滴和砂粒的轴向速度图。由图中可以看出，两种颗粒速度变化受流体粘度影响较小，并且沿裂缝中心处成轴对称分布。油滴速度略大于砂粒速度，两种颗粒初始速度约为零，随着流体的冲击作用，速度增大到流体速度大小的1/4，由此可见，流体的流动可以有效的携带颗粒运动。

图6 不同粘度下油滴-砂粒轴向速度

2.3 液相速度对颗粒流动特性的影响

在同一粘度的条件下，改变液体的速度观察颗粒运动特性，图7分别是油滴和砂粒的轴向速度图。由图中可以看出，随着流体速度增大，两种颗粒速度都明显增大，而油滴的运动更为剧烈，最大速度约是砂粒的2.5倍。砂粒运动相对平缓，这是由于砂粒密度比油滴大，所以受流体作用力相对较小。

图7 不同速度下油滴-砂粒轴向速度

2.4 固相砂粒密度对流动的影响

在模拟流动中密度大的颗粒在流动中更容易发生沉降，颗粒的停留时间增大。在砂粒密度为2 500 kg/m3时，微裂缝中颗粒整体呈向下的旋转流动，说明固体颗粒的密度对整个流场有很大的作用力影响。

图8 不同密度下砂粒轴向速度图

图9 不同密度下液体轴向速度图

图8-图9分别是以砂粒密度为变量的条件下固液两相瞬时轴向速度图，由图可知，密度越大，砂粒脉动越剧烈，而密度对液体流动状态的影响较小，随着固相砂粒密度的增大，液体速度的波动范围有减小的趋势。

3 结 论

对储层裂微缝进行系统结构的分析，应用Gambit建模软件完成对裂缝二维模型的建立。在以液固两相流的基本理论为基础，采用欧拉-拉格朗日双流体模型，建立数学模型，应用Fluent软件对微裂缝内固液两相流动状态进行数值模拟。结果表明Fluent 可以在拉氏坐标下模拟流场中离散的第二相，由球形颗粒（代表油滴和砂粒）构成的第二相分布在连续相中，并且可以计算这些颗粒的运动轨迹以及由颗粒引起的能量传递。通过单一变量方法模拟案比较不同条件下的流动状态，发现当液体入口速度相对较大时、颗粒运动速度也越大，但并不成正比；颗粒的停留时间减小。而液体粘度对流动的影响较大，当液体粘度增大时，颗粒运移明显，表现为颗粒停留计算域时间更短。固相密度能明显的影响颗粒的运动轨迹，密度大的颗粒在流动中更容易发生沉降。随着运动颗粒密度的增大，颗粒的瞬时轴向速度减小，颗粒的停留时间增大。颗粒密度的大小对液相流动状态的影响表现为：随着固相颗粒密度的增大，液相速度的波动范围有减小的趋势。

［1］纪友亮.油气储层地质学[M].第2版.东营：中国石油大学出版社,2009:6-7.

［2］ Tannenbaum, E., Huiainga, B., Kaplan, I.. Role of minerals in thermal alteration of organic matter. II—a material balance[J]. American Association of Petroleum Geologists Bulletin, 1986,70:1156-1165.

［3］王尤富.疏松砂岩地层微细粒运移特征实验研究[J].特种油气藏,2005,12(5):91-92.

［4］Gao P, Peterson S L. Favre-Marinet M. Seale Effects on Hydrodynamics and Heat Transfer in Two-dimensiolal Mini and Microchannels [J]. Int. J. Ther. Sei, 2002, 41 (11): 1017-1027.

［5］Pfund D A, Shekarriz A, Popescu A, et al. Pressure Drops Measurements in Microchannels[J]. Proceedings of MEMS, ASME DSC. 1998 (66): 193-198.

［6］Herwig H, Hausner O. Critical View on“New Results in Micro-fluid Mechanics”an Example[J]. Int. J. Heat and Mass Transfer, 2003(46): 935-937.

［7］Guo Z Y, Li Z X. Size Effect on Microscale Single-phase Flow and Heat Transfer[J]. Int. J. Heat and Mass Transfer, 2003 (46): 149-159.

［8］刘君.微通道流动特性的数值分析[D].哈尔滨工业大学,2010.

［9］聂海宽,张金川,张培先,等.福特沃斯盆地Bamet页岩气藏特征及启动［J］.地球科学进展，2009,28（2）：87-93.

［10］Gidaspow, D., Multiphase flow and fluidization: continuum and kinetic theory descriptions[M]. Academic Press, San Diego, 1994.

［11］王嘉骏，顾雪萍，杨富军，冯连芳，双流体模型中曳力及恢复系数对气固流动的影响[J].高校化学工程学报，20，164-168，2006。

Study on Flow Characteristics of Liquid-solid Two-phase Flow in Microfractures

YANG Qian，CHEN Yan-chao

（Northeast Petroleum University, Heilongjiang Daqing 163318，China）

Numerical simulation of liquid-solid two-phase flow in micro-fractures was carried out by Euler-Lagrange model. In the mathematical model, the liquid phase used the continuous phase model, the particles phase was treated as discrete phase dispersed in a continuous phase, and the coupling effect was considered. For the physical model, a two-dimensional direct micro-fracture model was established to study the effect of liquid viscosity, liquid velocity and particle density on the two-phase flow in fracture. The instantaneous distribution of particles in micro-fracture was obtained as well as the particle trajectory and particle retention time, particle axial velocity distribution, the variation law of the axial velocity distribution in liquid phase. The process of liquid-solid two-phase flow in micro-fracture reservoir was revealed qualitatively.

Micro-fracture; Computational fluid dynamics; Discrete element method; Numerical simulation

TE 122

A

1671-0460（2016）06-1194-04

2016-04-15

杨倩，女，黑龙江大庆人，在读硕士研究生，就读于东北石油大学石油与天然气专业，研究方向：复杂流体力学。E-mail：1036573319@qq.com。